УСТОЙЧИВОСТЬ ЛИОФОБНЫХ ДИСПЕРСНЫХ СИСТЕМ УСТОЙЧИВОСТЬ лиофобной дисперсной

УСТОЙЧИВОСТЬ ЛИОФОБНЫХ ДИСПЕРСНЫХ СИСТЕМ

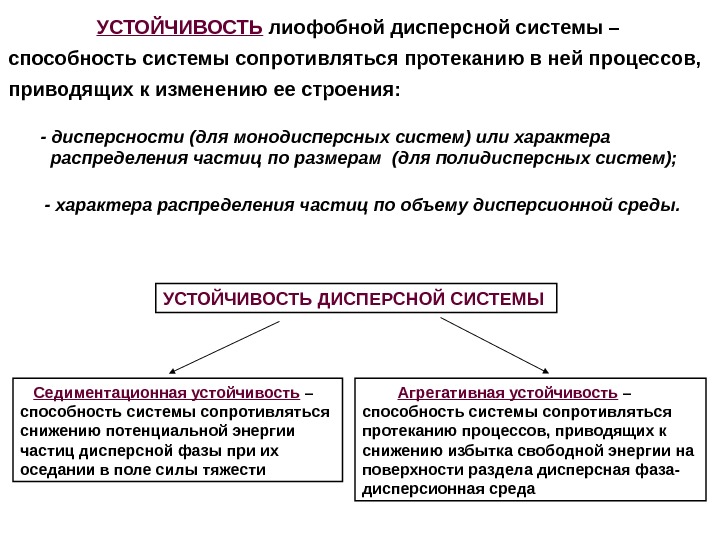
УСТОЙЧИВОСТЬ лиофобной дисперсной системы – способность системы сопротивляться протеканию в ней процессов, приводящих к изменению ее строения: УСТОЙЧИВОСТЬ ДИСПЕРСНОЙ СИСТЕМЫ Седиментационная устойчивость – способность системы сопротивляться снижению потенциальной энергии частиц дисперсной фазы при их оседании в поле силы тяжести Агрегативная устойчивость – способность системы сопротивляться протеканию процессов, приводящих к снижению избытка свободной энергии на поверхности раздела дисперсная фаза- дисперсионная среда- дисперсности (для монодисперсных систем) или характера распределения частиц по размерам (для полидисперсных систем); — характера распределения частиц по объему дисперсионной среды.

ТИПЫ УСТОЙЧИВОСТИ Седиментационная устойчивость Агрегативная устойчивость Седиментационно-устойчивая система Агрегативно-неустойчивая система Седиментационно-неустойчивая система

СЕДИМЕНТАЦИОННАЯ УСТОЙЧИВОСТЬ

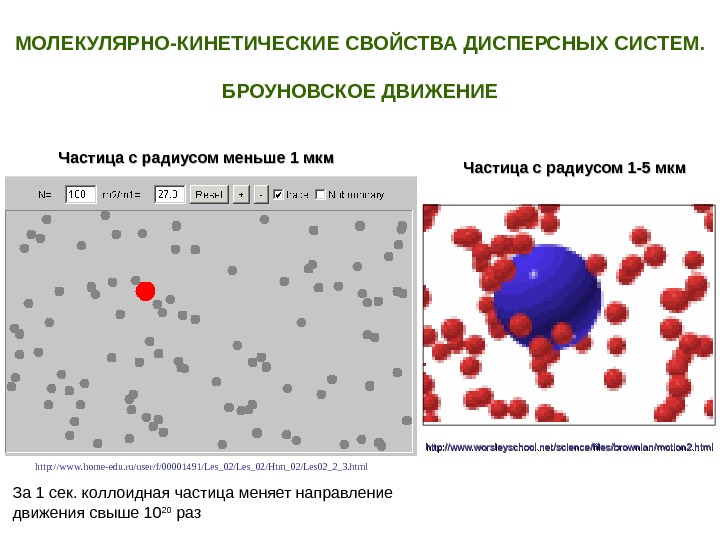
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЕ СВОЙСТВА ДИСПЕРСНЫХ СИСТЕМ. БРОУНОВСКОЕ ДВИЖЕНИЕ http: //www. home-edu. ru/user/f/00001491/Les_02/Htm_02/Les 02_2_3. html http: //www. worsleyschool. net/science/files/brownian/motion 2. html. Частица с радиусом меньше 1 мкм Частица с радиусом 1 -5 мкм За 1 сек. коллоидная частица меняет направление движения свыше 10 20 раз

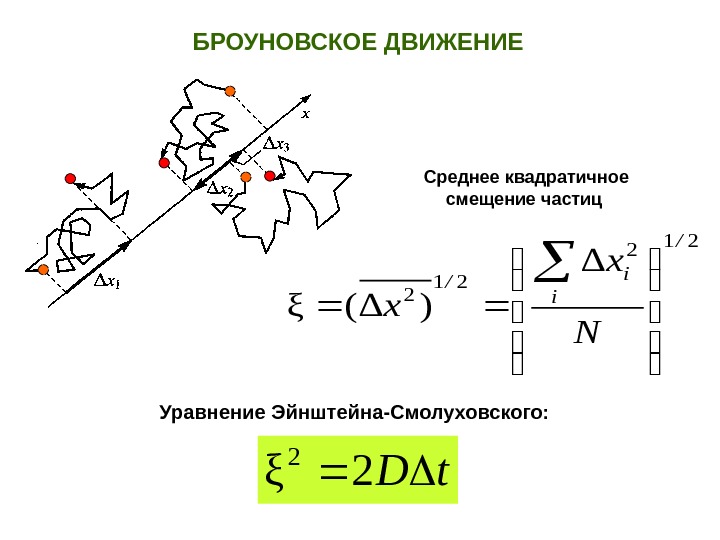
Среднее квадратичное смещение частиц t. D 2ξ 2 Уравнение Эйнштейна-Смолуховского: БРОУНОВСКОЕ ДВИЖЕНИЕ 212 21 2 Δ )Δ(ξ / i i/ N x x

ДИФФУЗИЯ В КОЛЛОИДНЫХ СИСТЕМАХ http: //www. home-edu. ru/user/f/00001491/Les_02/Htm_02/Les 02_2_3. html

ДИФФУЗИЯ В КОЛЛОИДНЫХ СИСТЕМАХdh dn Djдиф n BF vnj диф dhdn n. T dh nd. Tdhd F AAA N R N )ln(R N /μ dh dn B T n dh dn n. B T n B F j k N R AA диф r. Bπη 6 r T B T D πη 6 kk Первый закон Фика: Вывод уравнения Эйнштейна для коэфициента диффузии D : Уравнение Эйнштейна: Диффузия коллоидных частиц в воде: r, r, нмнм DD , , м м 22 // сс 11 4 4. . 1010 -10 -10 100100 4 4. . 1010 -14 —

ПОТОКИ, СУЩЕСТВУЮЩИЕ В ДИСПЕРСНЫХ СИСТЕМАХdh dn Djдифvnjсед mg. Fgrv. Bv. F 6 FFg r mg v 6 r k. T D 6 n r mg jсед 6 dh dn r k. T jдиф

j диф. > j сед. Седиментационно-устойчивые системы Высокодисперсные системы: золи j диф. < j сед. Седиментационно-неустойчивые системы Грубодисперсные системы: суспензии, эмульсии, взвеси j диф. = j сед. Седиментационно-диффузионное равновесие

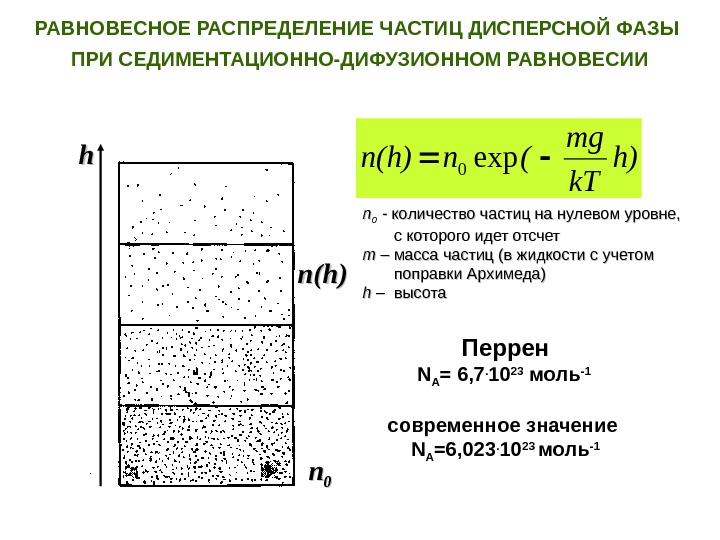
РАВНОВЕСНОЕ РАСПРЕДЕЛЕНИЕ ЧАСТИЦ ДИСПЕРСНОЙ ФАЗЫ ПРИ СЕДИМЕНТАЦИОННО-ДИФУЗИОННОМ РАВНОВЕСИИ hh h) k. Tmg (nn(h) exp 0 nn 00 n(h) Перрен N A = 6, 7. 10 23 моль -1 современное значение N A =6, 023. 10 23 моль -1 nn 0 0 — количество частиц на нулевом уровне, с которого идет отсчет m – масса частиц (в жидкости с учетом поправки Архимеда) hh – – высота

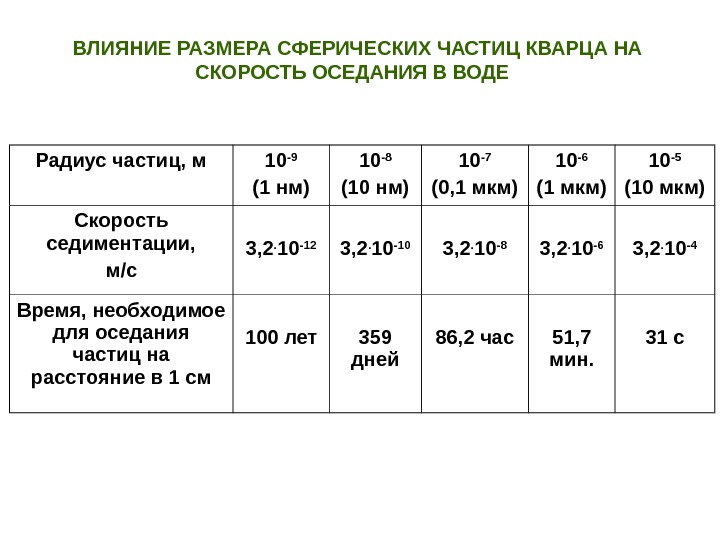
ВЛИЯНИЕ РАЗМЕРА СФЕРИЧЕСКИХ ЧАСТИЦ КВАРЦА НА СКОРОСТЬ ОСЕДАНИЯ В ВОДЕ Радиус частиц, м 10 -9 (1 нм) 10 -8 (10 нм) 10 -7 (0, 1 мкм) 10 -6 (1 мкм) 10 -5 (10 мкм) Скорость седиментации, м / с 3, 2. 10 -12 3, 2. 10 -10 3, 2. 10 -8 3, 2. 10 -6 3, 2. 10 -4 Время, необходимое для оседания частиц на расстояние в 1 см 100 лет 359 дней 86, 2 час 51, 7 мин. 31 с

АГРЕГАТИВНАЯ УСТОЙЧИВОСТЬ

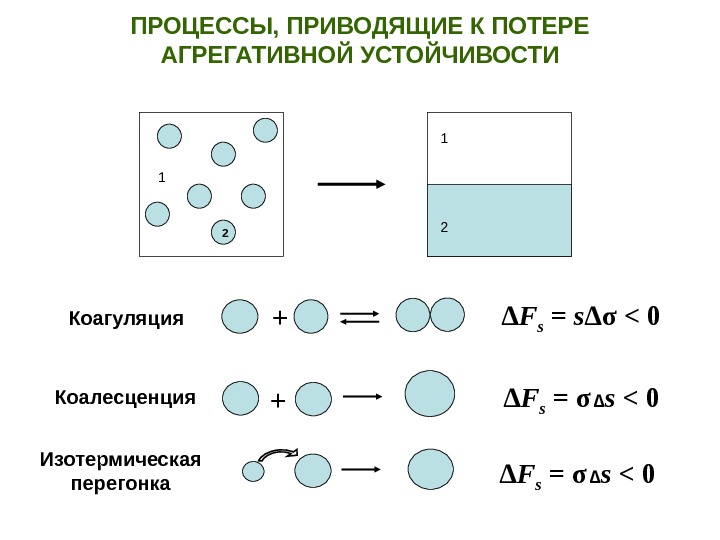
ПРОЦЕССЫ, ПРИВОДЯЩИЕ К ПОТЕРЕ АГРЕГАТИВНОЙ УСТОЙЧИВОСТИ 21 1 2 ∆ F s = s∆ σ < 0 Коагуляция + ∆ F s = σ ∆ s < 0 Изотермическая перегонка +Коалесценция ∆ F s = σ ∆ s <

h h > 2 δ Сближение δδ σ σ h < 2 δТОНКИЕ ПЛЕНКИ. РАСКЛИНИВАЮЩЕЕ ДАВЛЕНИЕ 1 1 2 F пл ( h ) = 2 σ + ∆ F пл ( h ) = 2 σdh h. Fd h )( )( пл [ Н / м 2 ] [ Дж / м 3 ]Π ( h )1 м

РАСКЛИНИВАЮЩЕЕ ДАВЛЕНИЕ П( h ) – это избыточное давление, которое необходимо приложить к ограничивающим пленку поверхностям, чтобы толщина пленки h оставалась постоянной или могла быть обратимо изменена в термодинамически равновесном процессе. 1. Молекулярная составляющая П mol — отрицательная роль в устойчивости 2. Электростатическая составляющая П el — положительная роль в устойчивостиh Слюда Вода h , мкм П( h ), Па 1 430 0, 04 188 . 10 2 Слюда Составляющие расклинивающего давления: П( h )= П mol + П el

МОЛЕКУЛЯРНАЯ СОСТАВЛЯЮЩАЯ РАСКЛИНИВАЮЩЕГО ДАВЛЕНИЯ 2 π12 h. A U mol 2 π12 h A Umol 3 π6 h A dh d. Umol A ~ α м 2 n 2 α м – поляризуемость молекул n – количество взаимодействующих молекул Для дисперсных систем. Простая константа Гамакера Сложная константа Гамакера A * = A 11 + A 22 — 2 A 12 = ( A 11 1/2 – A 22 1/2 ) 2 3 π6 h. A dhd. U mol [ Дж / м 2 ] [ Дж / м 3 ]

h 2 δ δ φ 0 δφ φ 0 δ φЭЛЕКТРОСТАТИЧЕСКАЯ СОСТАВЛЯЮЩАЯ РАСКЛИНИВАЮЩЕГО ДАВЛЕНИЯ x x

δexpγk 64)( 2 0 h Tnh el 22 0 0 2 kεε δ ezn T n 0 – концентрация электролита; k – константа Больцмана; δ – эффективная толщина ионной атмосферы. ЭЛЕКТРОСТАТИЧЕСКАЯ СОСТАВЛЯЮЩАЯ РАСКЛИНИВАЮЩЕГО ДАВЛЕНИЯ T ze k 4 thγ

ТЕОРИЯ ДЛФО (ТЕОРИЯ ДЕРЯГИНА, ЛАНДАУ, ФЕРВЕЯ, ОВЕРБЕКА)2 2 0 π12δ expδγk 64)( h Ah Tnh. U 3 2 0 π6δ expγk 64)( h Ah Tnh

U Σ (h) П Σ ( h ) Отталкивание Притяжение. ТЕОРИЯ ДЛФО

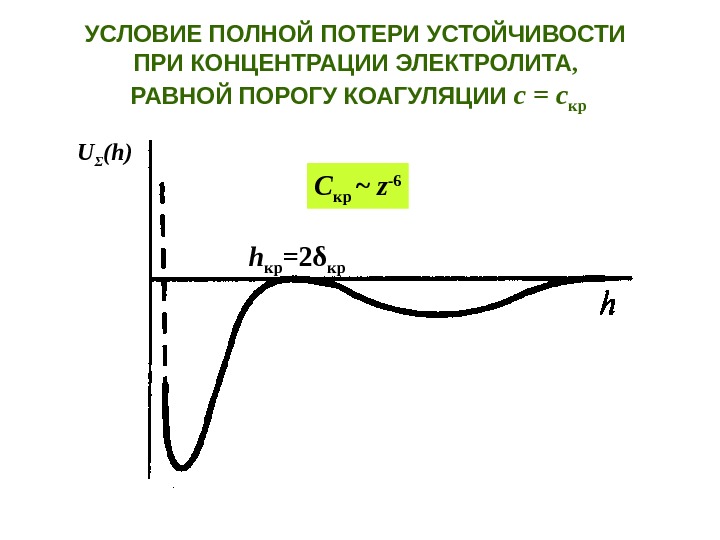
U Σ ( h ) h кр = 2 δ кр. УСЛОВИЕ ПОЛНОЙ ПОТЕРИ УСТОЙЧИВОСТИ ПРИ КОНЦЕНТРАЦИИ ЭЛЕКТРОЛИТА , РАВНОЙ ПОРОГУ КОАГУЛЯЦИИ с = с кр С кр ~ z —

КРИТЕРИЙ ЭЙЛЕРСА-КОРФА ПРАВИЛО ШУЛЬЦЕ-ГАРДИ С кр ( 1 ±) : С кр ( 2 ±) : С кр ( 3 ±) = 1 : 0, 016 : 0, 0015 С кр ~ z -6 кр 2 кр = const 2 > const – в системе коагуляции не происходит 2 < const – в системе происходит коагуляция

ЗАВИСИМОСТЬ СКОРОСТИ КОАГУЛЯЦИИ ОТ КОНЦЕНТРАЦИИ ИНДИФФЕРЕНТНОГО ЭЛЕКТРОЛИТА V коаг с кр

ЗОНЫ КОАГУЛЯЦИИ Z 21 k. T’β U к [ β ’ = ln(n а /n п ) ]кр кр V коаг- + {(m. Ag. I) n. I — (n-x)K + } x- x. K +Ag. NO 3 Al(NO 3 )

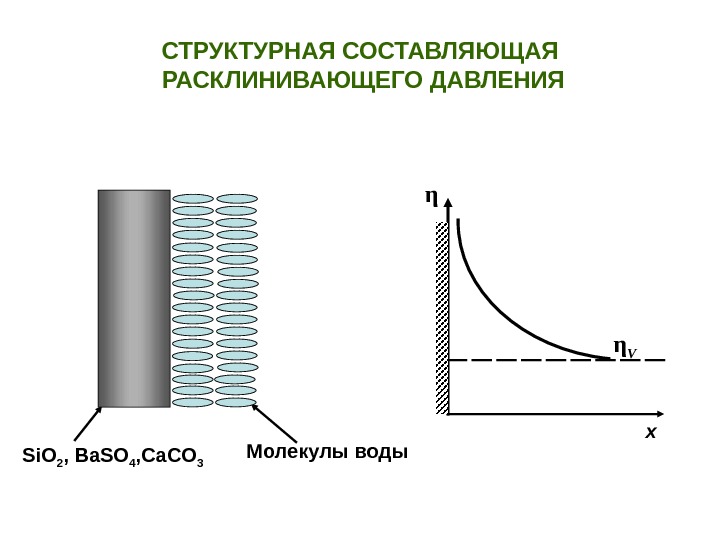
Молекулы воды Si. O 2 , Ba. SO 4 , Ca. CO 3 СТРУКТУРНАЯ СОСТАВЛЯЮЩАЯ РАСКЛИНИВАЮЩЕГО ДАВЛЕНИЯ η η V x

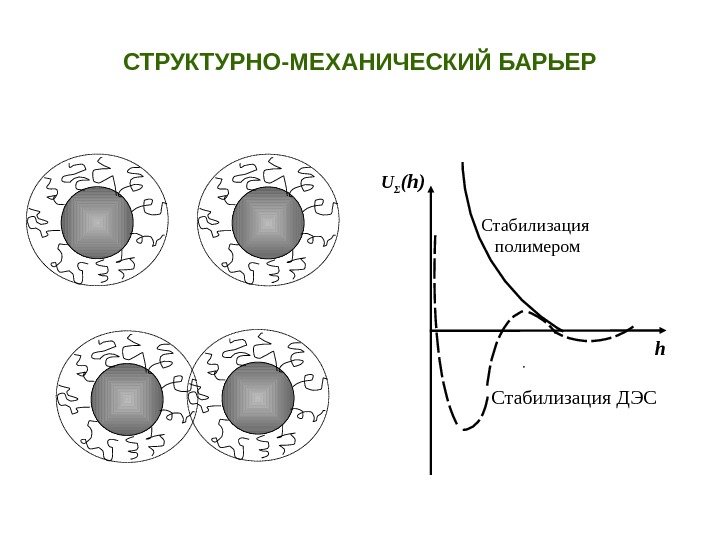
. U Σ (h) h. Стабилизация полимером Стабилизация ДЭССТРУКТУРНО-МЕХАНИЧЕСКИЙ БАРЬЕР

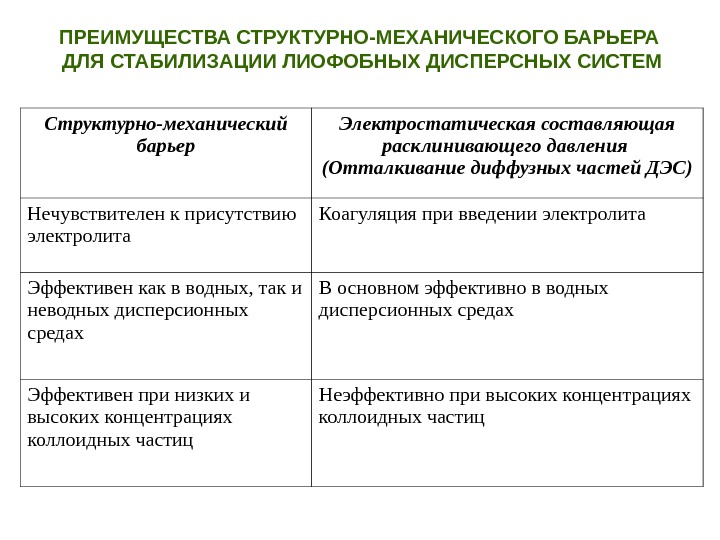
Структурно-механический барьер Электростатическая составляющая расклинивающего давления (Отталкивание диффузных частей ДЭС) Нечувствителен к присутствию электролита Коагуляция при введении электролита Эффективен как в водных, так и неводных дисперсионных средах В основном эффективно в водных дисперсионных средах Эффективен при низких и высоких концентрациях коллоидных частиц Неэффективно при высоких концентрациях коллоидных частиц. ПРЕИМУЩЕСТВА СТРУКТУРНО-МЕХАНИЧЕСКОГО БАРЬЕРА ДЛЯ СТАБИЛИЗАЦИИ ЛИОФОБНЫХ ДИСПЕРСНЫХ СИСТЕМ

ФАКТОРЫ СТАБИЛИЗАЦИИ ЛИОФОБНЫХ ДИСПЕРСНЫХ СИСТЕМ 1. Электростатическая составляющая расклинивающего давления (отталкивание диффузных частей ДЭС) 2. Структурная составляющая расклинивающего давления (гидратные оболочки вокруг частиц) 3. Структурно-механический барьер (гелеобразные слои ПАВ) 4. Лиофилизация поверхности частиц за счет адсорбции ПАВ 5. Сопротивление вязкой дисперсионной среды вытеканию из зазора между частицами

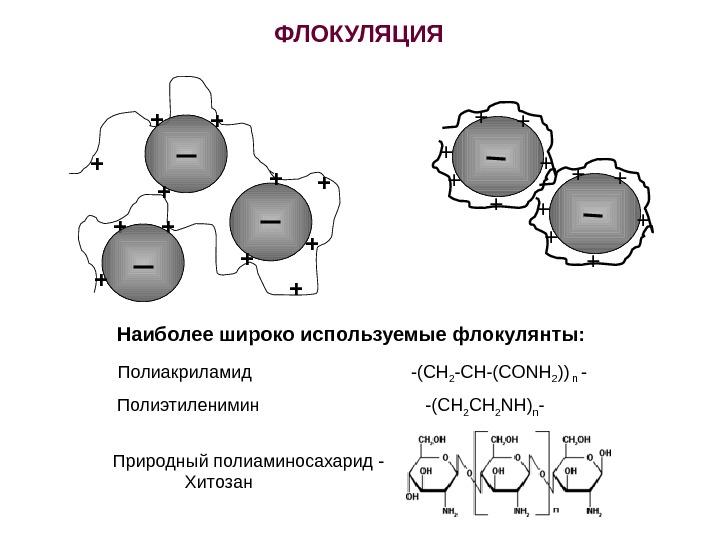
ФЛОКУЛЯЦИЯ +++ +++ + + ++ ++ + Полиакриламид -(CH 2 -CH-(CONH 2 )) n — Полиэтиленимин -(СН 2 NН) n -Наиболее широко используемые флокулянты: Природный полиаминосахарид — Хитозан