Устойчивость ГПС Понятие устойчивости Под устойчивостью гидропривода пневмопривода

Устойчивость ГПС

Понятие устойчивости Под устойчивостью гидропривода(пневмопривода) понимается его способность приходить в состояние устойчивого равновесия, после того как под влиянием какого-либо возмущающего воздействия привод был выведен из этого состояния. Возмущающие воздействия могут поступать: из внешней среды (например, изменение температуры), со стороны нагрузки (изменение массы, силы сопротивления), со стороны привода (изменение давления, расхода рабочей жидкости), со стороны системы управления (изменение перемещения, скоростей ускорения, органов управления).

Проверка устойчивости проводится, как правило, до исследования переходных процессов с помощью критериев устойчивости, рассматриваемых в теории автоматического регулирования. Эти критерии можно применять как к анализу устойчивости гидросистем с обратной связью, так и к анализу устойчивости движения любого гидроустройства или гидропривода без обратной связи.

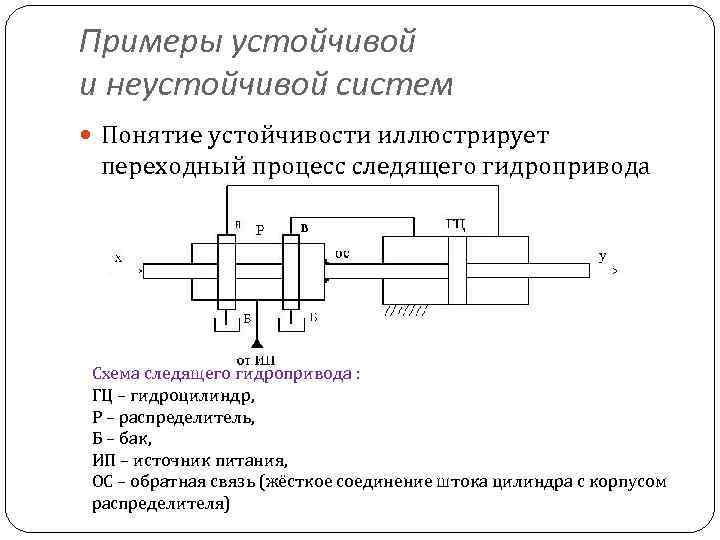Примеры устойчивой и неустойчивой систем Понятие устойчивости иллюстрирует переходный процесс следящего гидропривода Схема следящего гидропривода : ГЦ – гидроцилиндр, Р – распределитель, Б – бак, ИП – источник питания, ОС – обратная связь (жёсткое соединение штока цилиндра с корпусом распределителя)

При перемещении золотника вправо откроются проточки а и в. Поршень гидроцилиндра повторит перемещение золотника, т. е. перемещение поршня равно перемещению золотника распределителя Х при 0

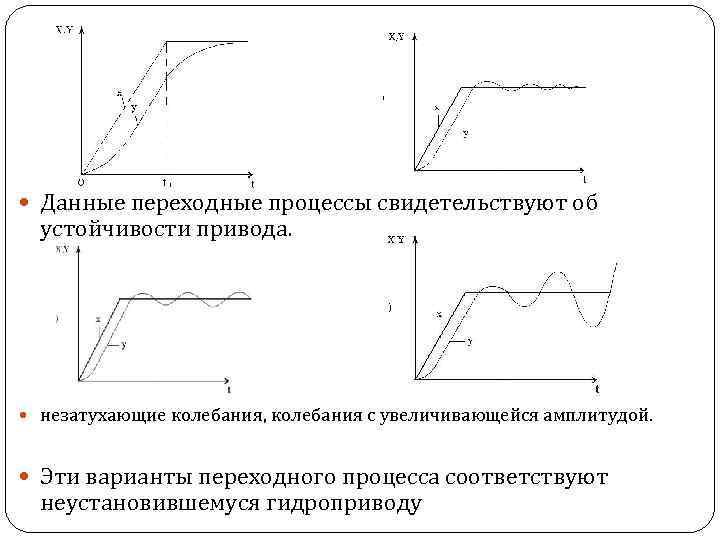Данные переходные процессы свидетельствуют об устойчивости привода. незатухающие колебания, колебания с увеличивающейся амплитудой. Эти варианты переходного процесса соответствуют неустановившемуся гидроприводу

Техническое определение устойчивости: Система устойчива, если её выходные параметры ограничены по величине в условиях длительного функционирования при ограниченных по величине возмущениях, которым она подвергается.

Методы решения задачи об устойчивости Для решения задачи об устойчивости ГПС используют: - гиперболу И. А. Вышнеградского, - диаграмму И. А. Вышнеградского, - критерий А. В. Михайлова, - критерий Э. Рауса и А. Гурвица, - критерий Г. Найквиста и другие методы…

Гипербола И. А. Вышнеградского строится для характеристического уравнения третьей степени a 3 S 3 + a 2 S 2 + a 1 S + a 0 =0, приведенного к нормированному виду Z 3 + АZ 2 + ВZ + 1 , где ; .

Если точка с координатами будет точно на гиперболе, то судить об устойчивости системы нельзя. Если точка с координатами А 1, В 1, расположена ниже гиперболы, то система неустойчива. Если точка с координатами А 2 и В 2, расположена выше гиперболы, то система устойчива

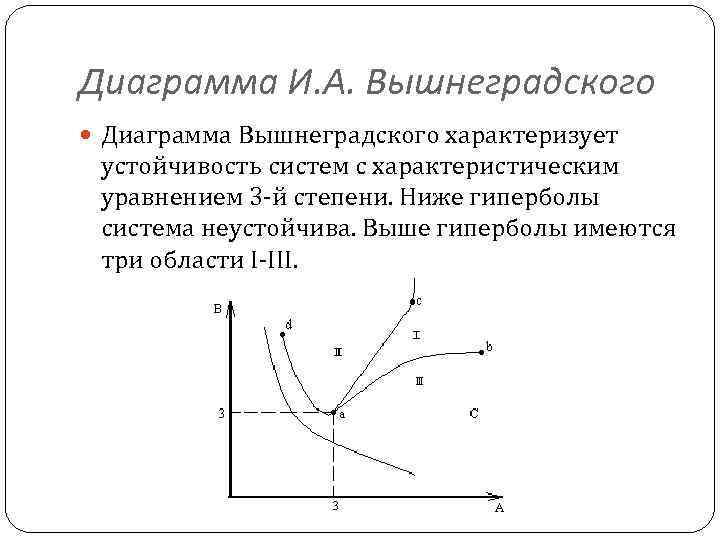Диаграмма И. А. Вышнеградского Диаграмма Вышнеградского характеризует устойчивость систем с характеристическим уравнением 3 -й степени. Ниже гиперболы система неустойчива. Выше гиперболы имеются три области I-III.

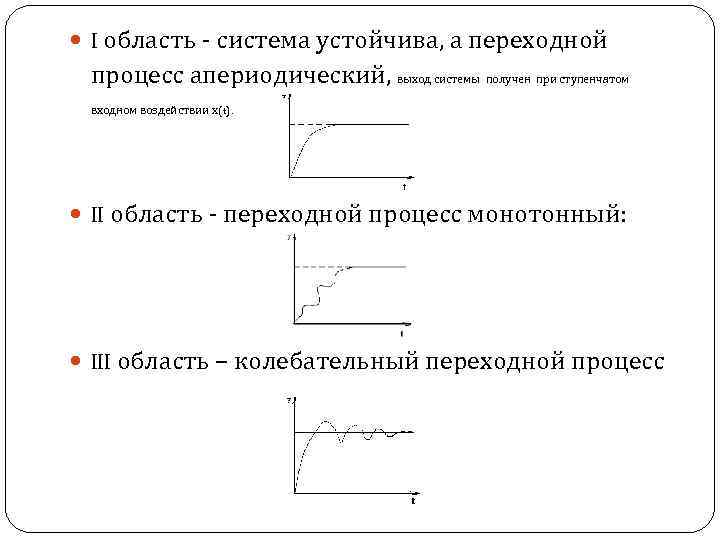I область - система устойчива, а переходной процесс апериодический, выход системы получен при ступенчатом входном воздействии х(t). II область - переходной процесс монотонный: III область – колебательный переходной процесс

Уравнения кривых, разграничивающих области I, III ab ac ad α=1, 2, 3…; Программа Math. Cad для построения диаграммы И. А. Вышнеградского

Критерий устойчивости А. В. Михайлова Характеристическое уравнение - это знаменатель передаточной функции W(S), приравненный нулю, т. е. если то характеристическое уравнение A(S)=0, Где S=iω, i= , 0≤ω<∞.

Критерий А. В. Михайлова Для устойчивости ГПС необходимо и достаточно, чтобы годограф вектора A(S) при 0≤ω≤∞ начинался на положительной части вещественной оси и в направлении против часовой стрелки последовательно проходил n квадрантов комплексной плоскости, где n- порядок характеристического уравнения Годограф - кривая, представляющая собой геометрическое место концов переменного (изменяющегося со временем) вектора, значения которого в разные моменты времени отложены от общего начала О. Годограф даёт наглядное геометрическое представление о том, как изменяется со временем физическая величина, изображаемая переменным вектором, и о скорости этого изменения, имеющей направление касательной к годографу.

Характеристическое уравнение имеет вид: при n=2 при n=3 при n=4 Программа Math. Cad для построения годографа Михайлова для устойчивой ГПС с характеристическим уравнением пятой степени.

Критерий Э. Рауса – А. Гурвица является алгебраическим. Для устойчивости ГПС необходимо и достаточно, чтобы определители матриц, составленные из коэффициентов характеристического уравнения, и все коэффициенты характеристического уравнения были больше нуля.

Правило составления матриц Если имеется характеристическое уравнение n -го порядка то матрица составляется следующим образом: Все пустые места заполняются нулями. Определители матриц более низкого порядка получают вычеркиванием последних строк и столбцов. Все определители, которые получают таким способом, должны быть больше нуля.

Пример

Вычисление i производится по следующей формуле где akj- элемент, который расположен в к-ой строке, j-ом столбце; Mkj-минор элемента akj, например, при . Минором некоторого элемента a ij определителя n-го порядка называется определитель (n-1)-го порядка, который получается, если в исходном определителе вычеркнуть строку и столбец, содержащие данный элемент. Минор элемента a ik обозначается Мik.