Условные числовые характеристики Для зависимых двухмерных величин могут

Условные числовые характеристики Для зависимых двухмерных величин могут быть определены условные законы распределения. Эти законы распределения обладают всеми свойствами безусловных законов, и на их основе по известным формулам могут бытьвычислены числовые характеристики, которые называются условными. Наибольшее практическое значение имеют условные математические ожидания.

Условное математическое ожидание случайной величины. Условным математическим ожиданием случайной величины Х называется ее математическое ожидание, вычисленное при условии, что случайная величина Y приняла определенное значение Y = y:

Условное математическое ожидание случайной величины.

Условное математическое ожидание случайной величины. Аналогично и для

Условное математическое ожидание случайной величины. Условное математическое ожидание называется регрессией X на y, а условное математическое ожидание − регрессией Y на х. Очевидно, что условные математические ожидания представляют собой некоторые функции, которых зависят от значения, взятого в условии а

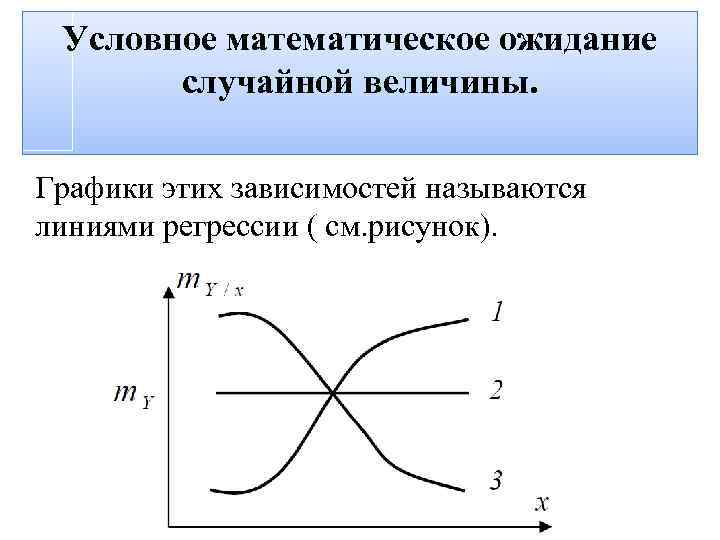Условное математическое ожидание случайной величины. Графики этих зависимостей называются линиями регрессии ( см. рисунок).

Условное математическое ожидание случайной величины. Линия регрессии 1 указывает, что между величинами X, Y существует положительная корреляционная зависимость, так как при увеличении значения х более вероятны большие значения Y (среднее значение Y увеличивается), т. е. >0

Условное математическое ожидание случайной величины. Линия регрессии 2 указывает, что величины X, Y независимы. А линия регрессии 3 – что между величинами X, Y существует отрицательная корреляционная зависимость, т. е. <0

Условное математическое ожидание случайной величины. Регрессионный анализ позволяет выявить характер связи между величинами X, Y. Величины X, Y называются линейно коррелированными, если линии регрессии являются прямыми. Уравнения прямых регрессии имеют вид: