67a634751c2256d5d2e50d00356566f6.ppt
- Количество слайдов: 119

Using Variables ALGEBRA 1 LESSON 1 -1 Write the operation (+, –, , ÷) that corresponds to each phrase. 1. divided by 2. difference 3. more than 4. product 5. minus 6. sum 7. multiplied by 8. quotient Find each amount. 9. 12 more than 9 10. 8 less than 13 11. 16 divided by 4 12. twice 25 1 -1
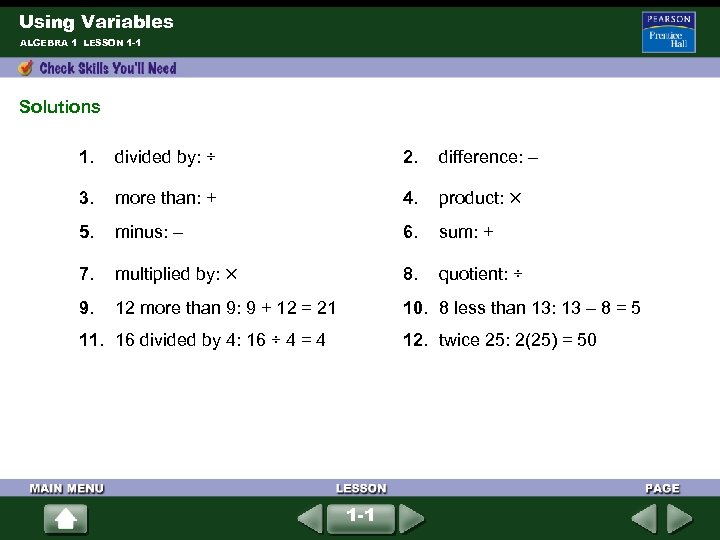
Using Variables ALGEBRA 1 LESSON 1 -1 Solutions 1. divided by: ÷ 2. difference: – 3. more than: + 4. product: 5. minus: – 6. sum: + 7. multiplied by: 8. 9. 12 more than 9: 9 + 12 = 21 10. 8 less than 13: 13 – 8 = 5 11. 16 divided by 4: 16 ÷ 4 = 4 quotient: ÷ 12. twice 25: 2(25) = 50 1 -1
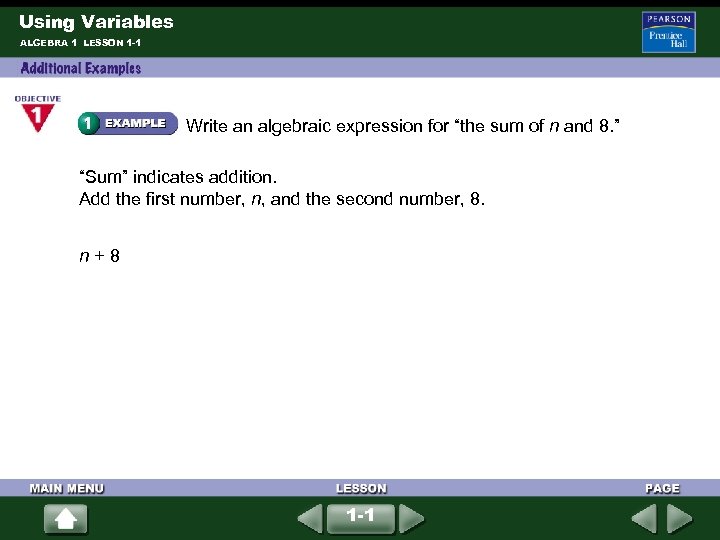
Using Variables ALGEBRA 1 LESSON 1 -1 Write an algebraic expression for “the sum of n and 8. ” “Sum” indicates addition. Add the first number, n, and the second number, 8. n + 8 1 -1
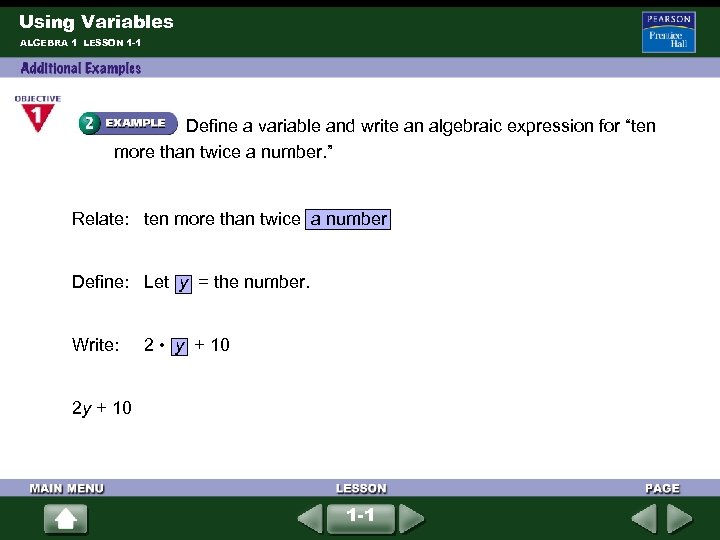
Using Variables ALGEBRA 1 LESSON 1 -1 Define a variable and write an algebraic expression for “ten more than twice a number. ” Relate: ten more than twice a number Define: Let y = the number. Write: 2 • y + 10 2 y + 10 1 -1
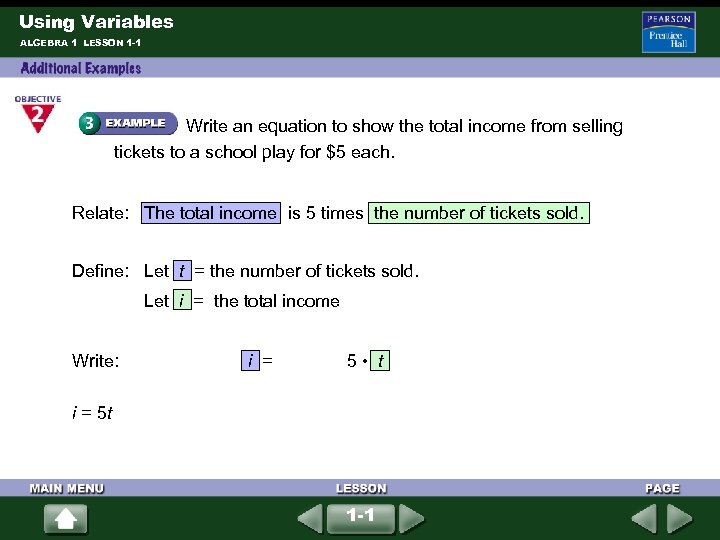
Using Variables ALGEBRA 1 LESSON 1 -1 Write an equation to show the total income from selling tickets to a school play for $5 each. Relate: The total income is 5 times the number of tickets sold. Define: Let t = the number of tickets sold. Let i = the total income Write: i = 5 • t i = 5 t 1 -1
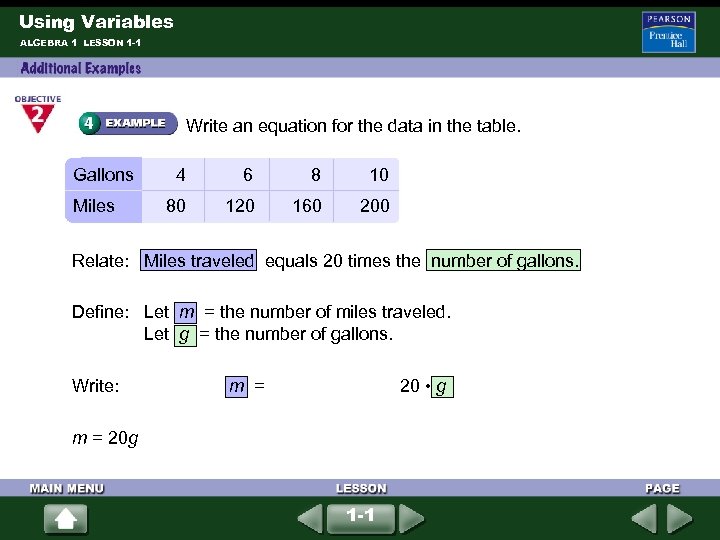
Using Variables ALGEBRA 1 LESSON 1 -1 Write an equation for the data in the table. Gallons Miles 4 6 8 10 80 120 160 200 Relate: Miles traveled equals 20 times the number of gallons. Define: Let m = the number of miles traveled. Let g = the number of gallons. Write: m = 20 • g m = 20 g 1 -1

Using Variables ALGEBRA 1 LESSON 1 -1 pages 6– 8 Exercises 1. p + 4 11. 9 – n 19. = total length in feet, n 82 2. y – 12 12. 3. 12 – m 13. 5 n 4. 15 c 14. 13 + 2 n n 5. 8 6. 17 k 15. 6 16. 11 7. x – 23 8. v + 3 9– 16. Choice of variable may vary. 9. 2 n + 2 10. n – 11 n = number of tents, = 60 n n 20. = number of slices left, e = number of slices eaten, = 8 – e n 17. c = total cost, n = number of cans, c = 0. 70 n 18. p = perimeter, s = length of a side, p = 4 s 1 -1

Using Variables ALGEBRA 1 LESSON 1 -1 21– 24. Choices of variables may vary. Samples are given. 25. 9 + k – 17 21. w = number of workers, 26. 5 n + 6. 7 r = number of radios, 27. 37 t – 9. 85 r = 13 w 28. 3 b 4. 5 35. the difference of 3 and t 22. n = number of tapes, 29. 15 + 60 c = cost, c = 8. 5 n 30. 7 – 3 v 23. n = number of sales, t = total earnings, t = 0. 4 n 24. n = number of hours, w 31. 5 m – t 7 p q 32. 14 + 3 33. 8 – 9 r p = pay, p = 8 n 1 -1 34– 38. Answers may vary. Samples are given. 34. 5 more than q 36. one more than the product of 9 and n 37. the quotient of y and 5 38. the product of 7 times h and b

Using Variables ALGEBRA 1 LESSON 1 -1 39– 40. Choices of variables may vary. Samples are given. worked would be a multiple of the number of lawns mowed. 42– 44. Choices of variables may vary. Samples are given. 39. n = number of days, c = change in height (m), 42. a. Let a = the amount in dollars c = 0. 165 n and n = the number of quarters, 40. t = time in months, a = 0. 25 q. = length in inches, b. $3. 25 = 4. 1 t 43. a. d = drop height (ft), 41. a. i. yes; 6 = 3 • 2 1 2 f = height of first bounce (ft), f = d ii. yes; 6 = 3 + 3 b. 10 ft b. Answers may vary. Sample: i; it makes sense that an equation relating lawns mowed and hours 44. s = height of second bounce (ft), 1 -1 1 s = d 4

Using Variables ALGEBRA 1 LESSON 1 -1 45– 47. Answers may vary. Samples are given. 45. You jog at a rate of 5 miles per hour. How far do you jog in 2 hours? Let d = distance in miles and t = time in hours. 46. Anabel is three years older than her brother Barry. How old will Anabel be when Barry is 12? Let a = Anabel’s age in years and b = Barry’s age in years. 47. The Merkurs have budgeted $40 for a baby sitter. What hourly rate can they afford to pay if they need the sitter for 5 hours? Let h = the number of hours and c the cost per hour. 48. D 60. 0. 14 49. H 61. 0. 93 50. A 62. 1 51. G 63. 0. 23 52. D 64. 3 53. F 65. 0. 11 54. 0. 9 66. any four of 23, 55. 1. 04 29, 31, 37, 41, 56. 1. 35 43, and 47 57. 1. 46 58. 0. 63 59. 0. 09 1 -1

Using Variables ALGEBRA 1 LESSON 1 -1 Write an algebraic expression for each phrase. 1. 7 less than 9 9 – 7 2. the product of 8 and p 8 p 3. 4 more than twice c 2 c + 4 Define variables and write an equation to model each situation. 4. The total cost is the number of sandwiches times $3. 50. Let c = the total cost and s = the number of sandwiches; c = 3. 5 s 5. The perimeter of a regular hexagon is 6 times the length of one side. Let p = the perimeter and s = the length of a side; p = 6 s 1 -1

Exponents and Order of Operations ALGEBRA 1 LESSON 1 -2 Find each product. 1. 4 • 4 2. 7 • 7 3. 5 • 5 Perform the indicated operations. 5. 3 + 12 – 7 6. 6 • 1 ÷ 2 7. 4 – 2 + 9 8. 10 – 5 – 4 9. 5 • 5 + 7 10. 30 ÷ 6 • 2 1 -2 4. 9 • 9
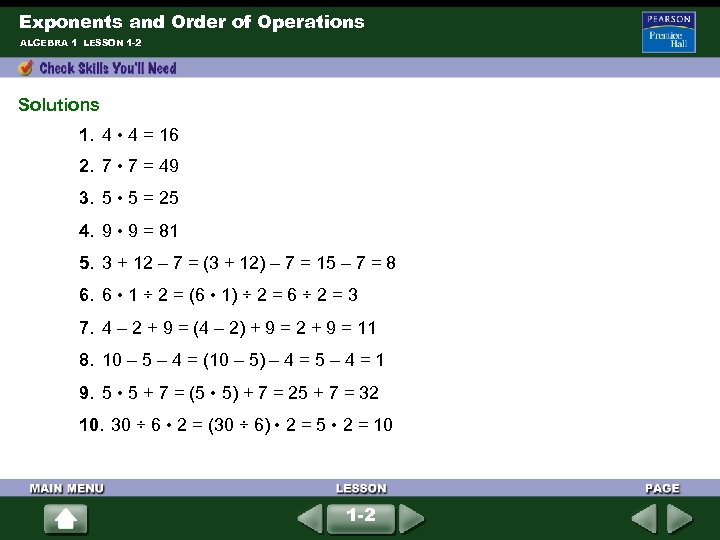
Exponents and Order of Operations ALGEBRA 1 LESSON 1 -2 Solutions 1. 4 • 4 = 16 2. 7 • 7 = 49 3. 5 • 5 = 25 4. 9 • 9 = 81 5. 3 + 12 – 7 = (3 + 12) – 7 = 15 – 7 = 8 6. 6 • 1 ÷ 2 = (6 • 1) ÷ 2 = 6 ÷ 2 = 3 7. 4 – 2 + 9 = (4 – 2) + 9 = 2 + 9 = 11 8. 10 – 5 – 4 = (10 – 5) – 4 = 5 – 4 = 1 9. 5 • 5 + 7 = (5 • 5) + 7 = 25 + 7 = 32 10. 30 ÷ 6 • 2 = (30 ÷ 6) • 2 = 5 • 2 = 10 1 -2
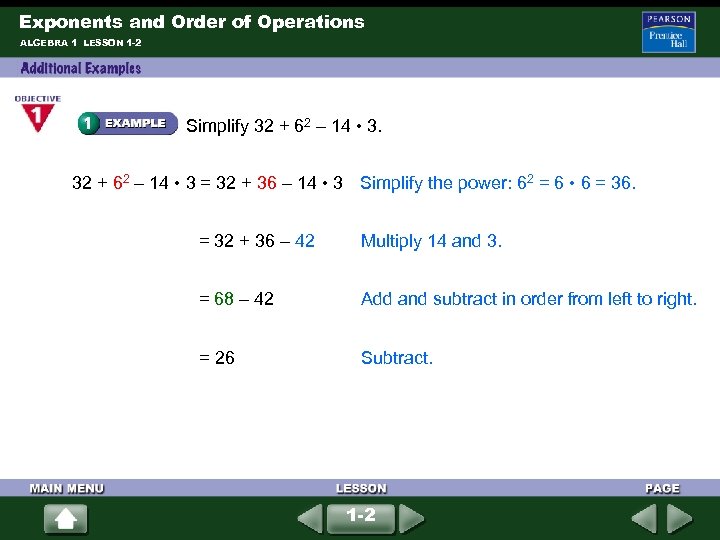
Exponents and Order of Operations ALGEBRA 1 LESSON 1 -2 Simplify 32 + 62 – 14 • 3 = 32 + 36 – 14 • 3 Simplify the power: 62 = 6 • 6 = 36. = 32 + 36 – 42 Multiply 14 and 3. = 68 – 42 Add and subtract in order from left to right. = 26 Subtract. 1 -2
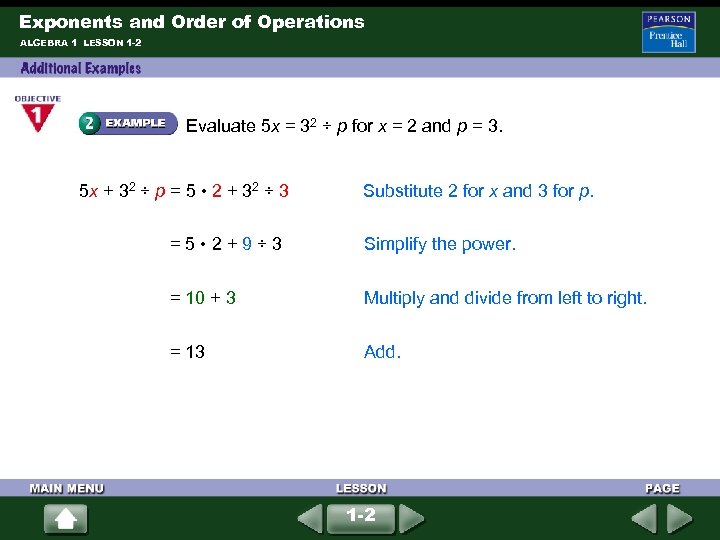
Exponents and Order of Operations ALGEBRA 1 LESSON 1 -2 Evaluate 5 x = 32 ÷ p for x = 2 and p = 3. 5 x + 32 ÷ p = 5 • 2 + 32 ÷ 3 Substitute 2 for x and 3 for p. = 5 • 2 + 9 ÷ 3 Simplify the power. = 10 + 3 Multiply and divide from left to right. = 13 Add. 1 -2
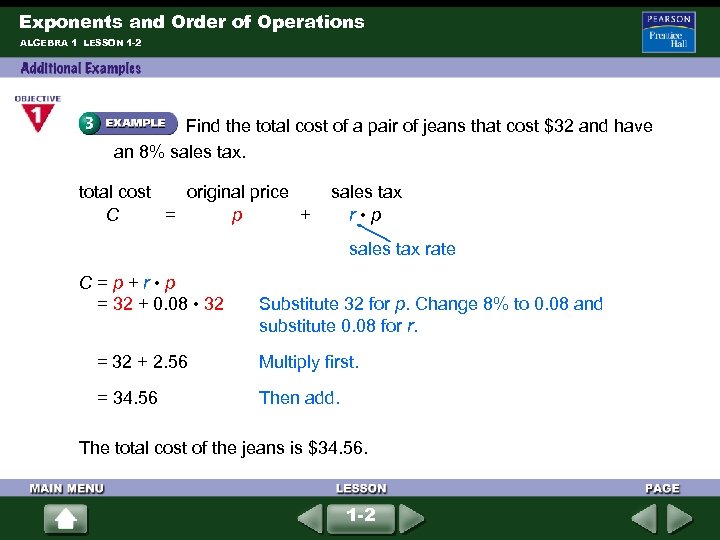
Exponents and Order of Operations ALGEBRA 1 LESSON 1 -2 Find the total cost of a pair of jeans that cost $32 and have an 8% sales tax. total cost original price sales tax C = p + r • p sales tax rate C = p + r • p = 32 + 0. 08 • 32 Substitute 32 for p. Change 8% to 0. 08 and substitute 0. 08 for r. = 32 + 2. 56 Multiply first. = 34. 56 Then add. The total cost of the jeans is $34. 56. 1 -2
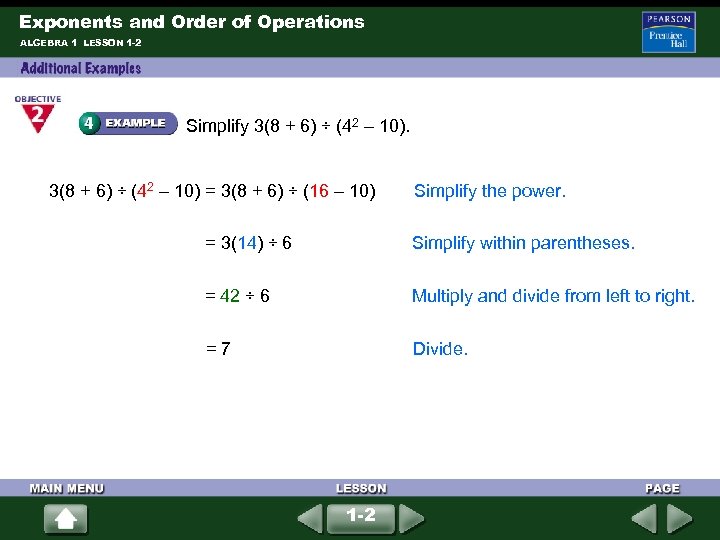
Exponents and Order of Operations ALGEBRA 1 LESSON 1 -2 Simplify 3(8 + 6) ÷ (42 – 10) = 3(8 + 6) ÷ (16 – 10) Simplify the power. = 3(14) ÷ 6 Simplify within parentheses. = 42 ÷ 6 Multiply and divide from left to right. = 7 Divide. 1 -2

Exponents and Order of Operations ALGEBRA 1 LESSON 1 -2 Evaluate each expression for x = 11 and z = 16. a. (xz)2 b. xz 2 (xz)2 = (11 • 16)2 Substitute 11 for x and 16 for z. = (176)2 Simplify within parentheses. Multiply. = 30, 976 Simplify. 1 -2 xz 2 = 11 • 162 = 11 • 256 = 2816
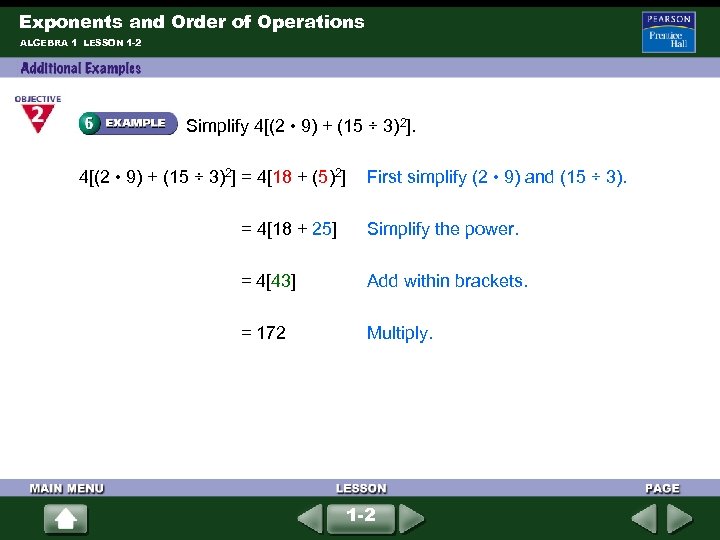
Exponents and Order of Operations ALGEBRA 1 LESSON 1 -2 Simplify 4[(2 • 9) + (15 ÷ 3)2] = 4[18 + (5)2] First simplify (2 • 9) and (15 ÷ 3). = 4[18 + 25] Simplify the power. = 4[43] Add within brackets. = 172 Multiply. 1 -2
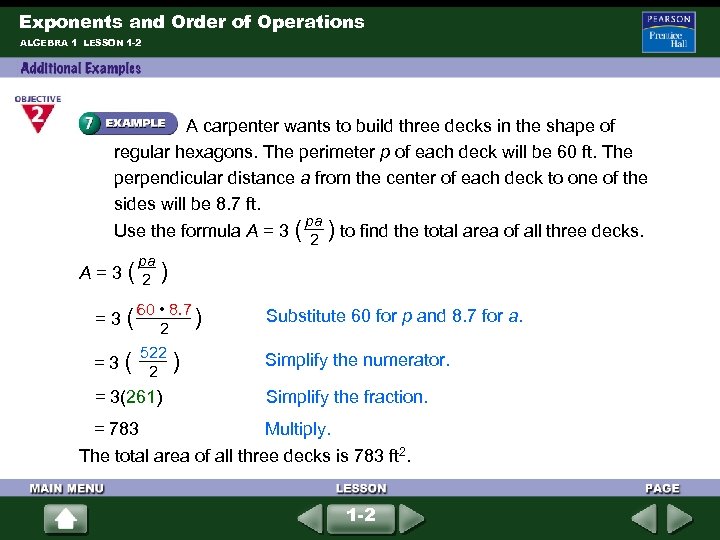
Exponents and Order of Operations ALGEBRA 1 LESSON 1 -2 A carpenter wants to build three decks in the shape of regular hexagons. The perimeter p of each deck will be 60 ft. The perpendicular distance a from the center of each deck to one of the sides will be 8. 7 ft. pa Use the formula A = 3 ( ) to find the total area of all three decks. 2 pa A = 3 ( ) 2 60 • 8. 7 Substitute 60 for p and 8. 7 for a. = 3 ( ) 2 522 Simplify the numerator. = 3(261) Simplify the fraction. = 3 ( ) 2 = 783 Multiply. The total area of all three decks is 783 ft 2. 1 -2
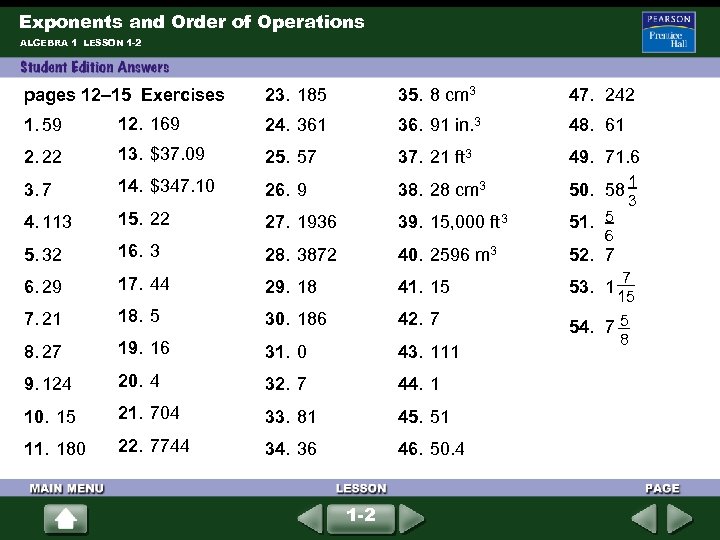
Exponents and Order of Operations ALGEBRA 1 LESSON 1 -2 pages 12– 15 Exercises 23. 185 35. 8 cm 3 47. 242 1. 59 12. 169 24. 361 36. 91 in. 3 48. 61 2. 22 13. $37. 09 25. 57 37. 21 ft 3 49. 71. 6 3. 7 14. $347. 10 26. 9 38. 28 cm 3 50. 58 4. 113 15. 22 27. 1936 39. 15, 000 ft 3 51. 5 5. 32 16. 3 28. 3872 40. 6. 29 17. 44 29. 18 41. 15 53. 1 15 7. 21 18. 5 30. 186 42. 7 54. 7 5 8. 27 19. 16 31. 0 43. 111 9. 124 20. 4 32. 7 44. 1 10. 15 21. 704 33. 81 45. 51 11. 180 22. 7744 34. 36 46. 50. 4 1 -2 2596 m 3 1 3 6 52. 7 7 8
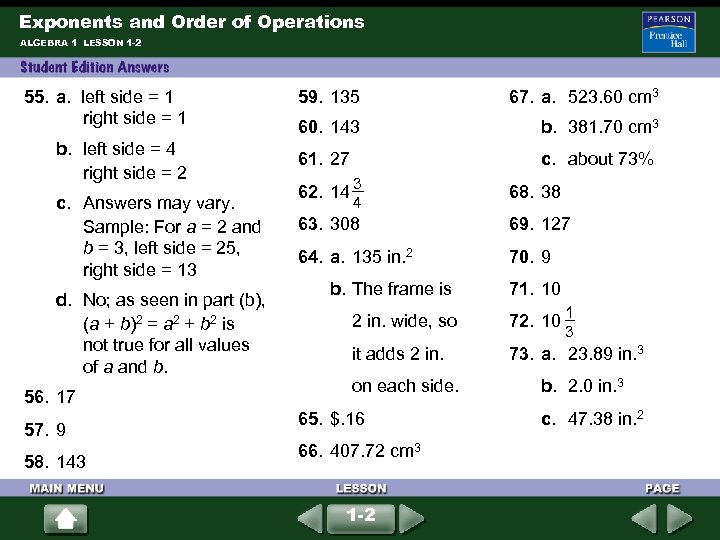
Exponents and Order of Operations ALGEBRA 1 LESSON 1 -2 55. a. left side = 1 right side = 1 b. left side = 4 right side = 2 c. Answers may vary. Sample: For a = 2 and b = 3, left side = 25, right side = 13 d. No; as seen in part (b), (a + b)2 = a 2 + b 2 is not true for all values of a and b. 56. 17 57. 9 58. 143 59. 135 67. a. 523. 60 cm 3 60. 143 b. 381. 70 cm 3 61. 27 c. about 73% 62. 14 3 4 68. 38 63. 308 69. 127 64. a. 135 in. 2 70. 9 b. The frame is 71. 10 2 in. wide, so 72. 10 it adds 2 in. 73. a. 23. 89 in. 3 on each side. 65. $. 16 66. 407. 72 cm 3 1 -2 1 3 b. 2. 0 in. 3 c. 47. 38 in. 2

Exponents and Order of Operations ALGEBRA 1 LESSON 1 -2 74. Yes; the rules for simplifying are designed to produce exactly one result. 75. (10 + 6) ÷ 2 – 3 = 5 76. 14 – (2 + 5) – 3 = 4 77. (32 + 9) ÷ 9 = 2 80. a. 16, 2 b. Yes; part (a) shows that the placement of parentheses can affect the value of the expression, when both add. and subtr. are involved. 81. Answers may vary. Samples: 78. (6 – 4) ÷ 2 = 1 2(4 – 1) – 5 = 1 5 + 2 – (1 + 4) = 2 79. a. 22; 22 (24 – 1) ÷ 5 = 3 b. No; part (a) shows the value is unaffected for the given numbers. 1 + 2 + 5 – 4 = 4 2 • 5 – (1 + 4) = 5 (52 – 1) ÷ 4 = 6 1 -2 5 + 4 – 1 • 2 = 7 25 ÷ (4 • 1) = 8 25 ÷ 4 + 1 = 9 42 – (1 + 5) = 10 (42 – 5) ÷ 1 = 11 1 + 2 + 4 + 5 = 12 2(4 – 1) + 5 = 13 2 • 5 + 1 • 4 = 14 5(4 – 12) = 15 2(1 + 5) + 4 = 16 5 + 4(2 + 1) = 17 4(5 – 1) + 2 = 18 4 • 5 – 12 = 19 42 + 5 – 1 = 20

Exponents and Order of Operations ALGEBRA 1 LESSON 1 -2 82. a. 38 ft 2 b 1 + b 2 = 2 h 2 2 b 1 + b 2 / No; h = 2 h b 1 + b 2 2 2 b. Yes; 2 h 95. 95%. 2 h 96. 145% 106. 26, 39, 52 97. 6% 98. 43 / since b 2 = 0. Yes; h 105. 60, 150, 240 2(b 1 + b 2) = h = 2 2 b 1 + b 2. 2 99. 18. 9 100. 1. 25 101. 60. 3 102– 106. Answers may vary. Samples are given. 83. D 87. B 91. t – 21 84. F 88. F 92. y 102. 8, 24, 56 85. B 89. c + 2 93. 50% 103. 55, 100, 250 86. H 90. 36 m 94. 34% 104. 44, 66, 121 5 1 -2
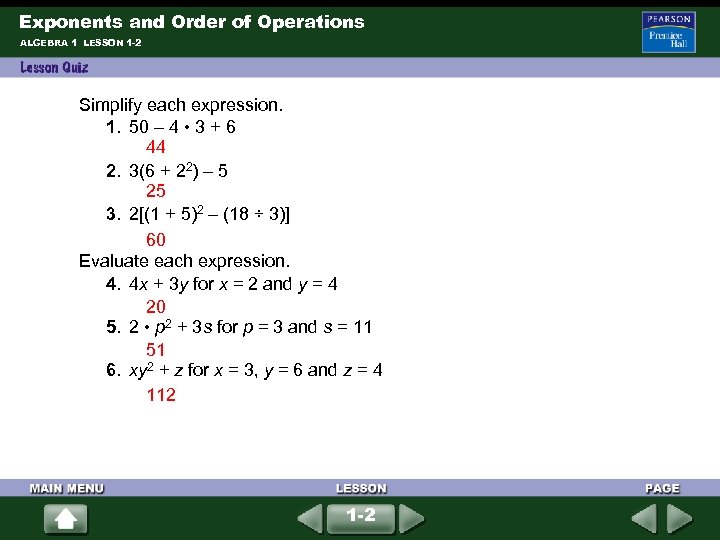
Exponents and Order of Operations ALGEBRA 1 LESSON 1 -2 Simplify each expression. 1. 50 – 4 • 3 + 6 44 2. 3(6 + 22) – 5 25 3. 2[(1 + 5)2 – (18 ÷ 3)] 60 Evaluate each expression. 4. 4 x + 3 y for x = 2 and y = 4 20 5. 2 • p 2 + 3 s for p = 3 and s = 11 51 6. xy 2 + z for x = 3, y = 6 and z = 4 112 1 -2

Exploring Real Numbers ALGEBRA 1 LESSON 1 -3 (For help, go to skills handbook page 725. ) Write each decimal as a fraction and each fraction as a decimal. 1. 0. 5 5. 2 5 2. 0. 05 6. 3 8 3. 3. 25 7. 1 -3 2 3 4. 0. 325 8. 3 5 9
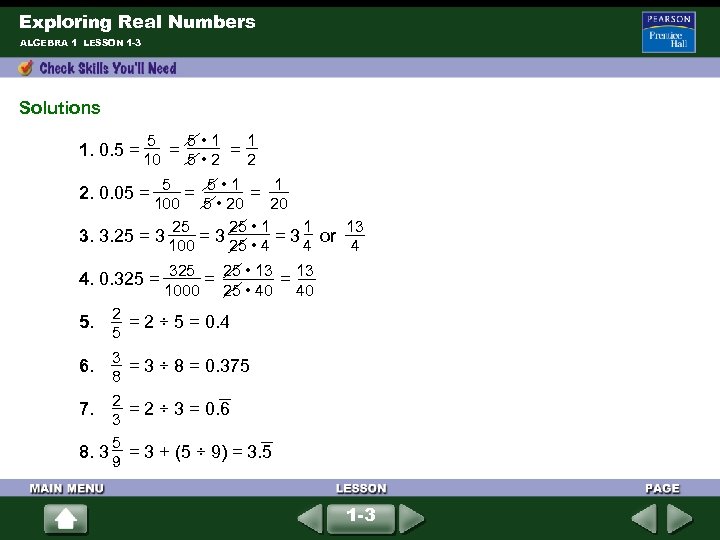
Exploring Real Numbers ALGEBRA 1 LESSON 1 -3 Solutions 5 10 5 • 1 5 • 2 1. 0. 5 = = 5 5 • 1 1 100 5 • 20 20 25 • 1 1 25 13 3. 3. 25 = 3 or 25 • 4 4 100 4 2. 0. 05 = = = 325 25 • 13 4. 0. 325 = = 13 1000 25 • 40 40 2 5 5. = 2 ÷ 5 = 0. 4 3 8 2 7. = 2 ÷ 3 = 0. 6 3 5 8. 3 = 3 + (5 ÷ 9) = 3. 5 9 6. = 3 ÷ 8 = 0. 375 1 -3
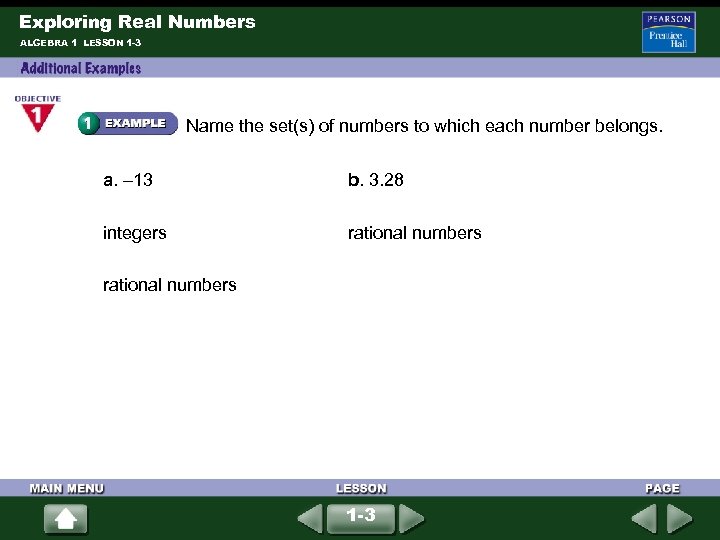
Exploring Real Numbers ALGEBRA 1 LESSON 1 -3 Name the set(s) of numbers to which each number belongs. a. – 13 b. 3. 28 integers rational numbers 1 -3
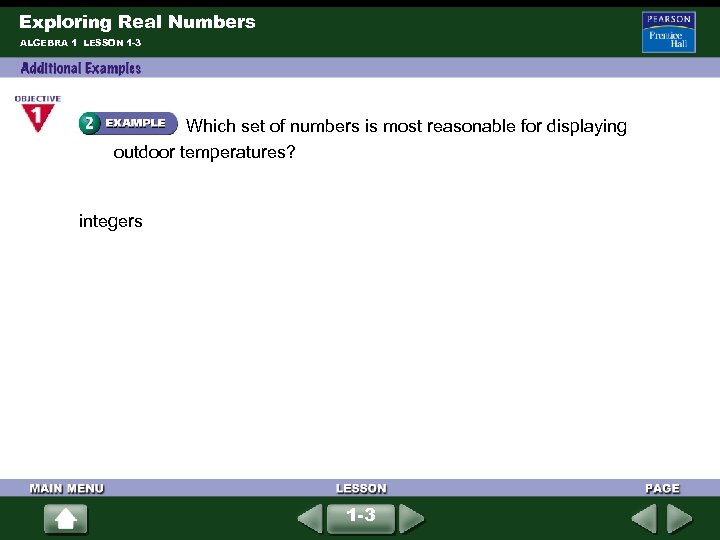
Exploring Real Numbers ALGEBRA 1 LESSON 1 -3 Which set of numbers is most reasonable for displaying outdoor temperatures? integers 1 -3

Exploring Real Numbers ALGEBRA 1 LESSON 1 -3 Determine whether the statement is true or false. If it is false, give a counterexample. All negative numbers are integers. 2 3 A negative number can be a fraction, such as – . This is not an integer. The statement is false. 1 -3
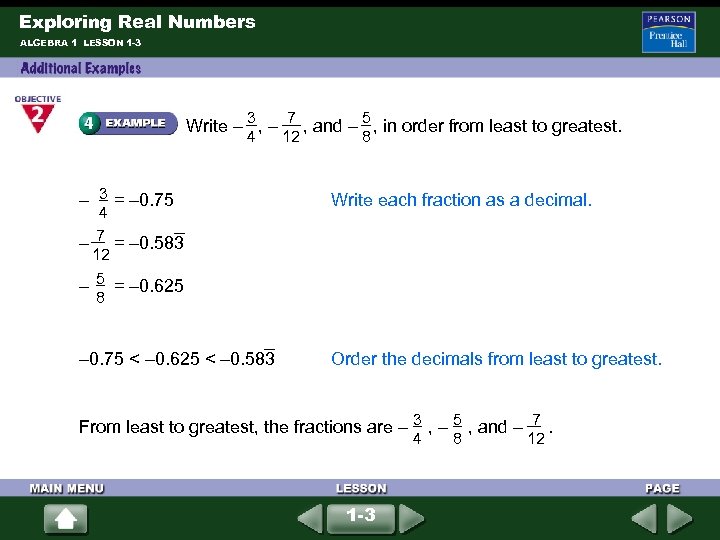
Exploring Real Numbers ALGEBRA 1 LESSON 1 -3 3 4 7 12 5 8 Write – , – , and – , in order from least to greatest. 3 – = – 0. 75 Write each fraction as a decimal. – 0. 75 < – 0. 625 < – 0. 583 Order the decimals from least to greatest. 4 7 – = – 0. 583 12 5 – = – 0. 625 8 3 5 7 From least to greatest, the fractions are – , and – . 4 1 -3 8 12
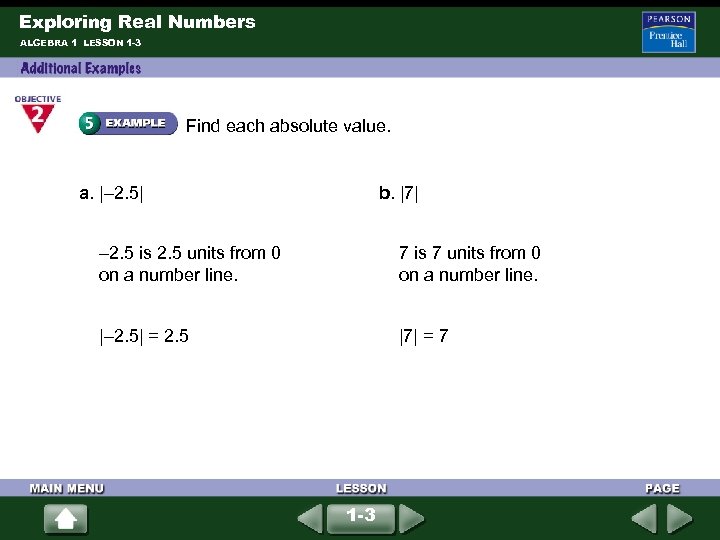
Exploring Real Numbers ALGEBRA 1 LESSON 1 -3 Find each absolute value. a. |– 2. 5| b. |7| – 2. 5 is 2. 5 units from 0 on a number line. 7 is 7 units from 0 on a number line. |– 2. 5| = 2. 5 |7| = 7 1 -3

Exploring Real Numbers ALGEBRA 1 LESSON 1 -3 pages 20– 23 Exercises 9. rational numbers 1. integers, rational numbers 10. irrational numbers 2. rational numbers 3. rational numbers 18. rational numbers 19. true 11. Answers may vary. 20. False; answers may vary. Sample: – 17 Sample: – 2 3 4. natural numbers, 12. Answers may vary. 21. False; answers may vary. whole numbers, integers, Sample: 53 Sample: 6 rational numbers 13. Answers may vary. 22. true 5. rational numbers 6. integers, rational numbers Sample: 0. 3 7. whole numbers, integers, 14. rational numbers 15. whole numbers 8. rational numbers 16. integers 17. whole numbers 1 -3 23. False; answers may vary. Sample: – 6 < | – 6 | 24. > 25. < 26. >

Exploring Real Numbers ALGEBRA 1 LESSON 1 -3 27. = 39. 0 28. 2. 001, 2. 1 40. 1295 3 2 29. – 9 , – 9 7 41. 4 4 3 5 1 30. – , 2 6 2 3 12 7 32. 0. 63, 0. 636, 11 33. 22 , 0. 8888, 8 25 9 35. 9 36. 9 14 37. 0. 5 Sample: – 4 1 5 42. Answers may vary. 31. – 1. 01, – 1. 0009 34. 4 46. Answers may vary. Sample: 1 5 43. Answers may vary. Sample: 5 1 44. Answers may vary. Sample: 213 47. natural numbers, whole numbers, integers, rational numbers 48. natural numbers, whole numbers, integers, rational numbers 10 45. Answers may vary. Sample: 1034 1000 38. 3 5 1 -3 49. rational numbers 50. rational numbers

Exploring Real Numbers ALGEBRA 1 LESSON 1 -3 51. = 52. > 63. a. irrational b. No; has no final digit. 67. Answers may vary. Sample: 25, |25| + | – 25| = 50 68. sometimes 53. < 64. 0 54. > 69. sometimes 65. Neg. ; 0 is the point between R and S since the coordinates 70. sometimes of Q and T are opposites, 71. always so if R is to the left of 0, then R is neg. 72. Yes; all can be expressed as ratios of themselves to 1. 66. Q; 0 is the point to the right 55. = 56. > 57. 6 58. 9 59. a 60. 28 61. 48 of S because the coordinates of R and T are opposites, therefore the point Q is the farthest from 0, so it has the greatest absolute value. 62. 5 1 -3 73. – 6 74. 17 75. 1 76. 10

Exploring Real Numbers ALGEBRA 1 LESSON 1 -3 g g 77. a. 2. 75 , 19. 3 , cm 3 80. G 92. 25 10. 5 , 3. 5 cm 3 81. D 93. 4 b. aluminum, diamond, 82. G g g silver, gold 83. C 78. Answers may vary. 84. I 94. 195 95– 98. Choices of variables may vary. Samples are given. 85. C 95. n = number of tickets, 6. 25 n a. – 2. 2 86. 33 96. i = cost of item, i + 3. 98 b. – 2. 81 87. 48 97. n = number of hours, d = distance traveled, d = 7 n 1 c. – 2 8 d. Yes; find the average of the two given numbers. 79. A 88. 315 89. 7 90. 0 91. 7 1 2 1 -3 98. c = total cost, n = number of books, c = 3. 5 n

Exploring Real Numbers ALGEBRA 1 LESSON 1 -3 Name the set(s) of numbers to which each given number belongs. 1. – 2. 7 2. 11 rational numbers 3. 16 irrational numbers Use <, =, or > to compare. 4. 3 4 > 5. 5 8 – 3 < – 5 4 7 6. Find |– |. 12 7 12 1 -3 8 natural numbers, whole numbers integers, rational numbers

Adding Real Numbers ALGEBRA 1 LESSON 1 -4 (For help, go to skills handbook page 726. ) Find each sum. 1. 4 + 2 2. 10 + 7 3. 9 + 5 4. 27 + 32 5. 0. 4 + 0. 9 6. 5. 2 + 0 7. 4. 1 + 6. 8 8. 7. 6 + 9. 5 1 9. + 3 4 10. + 7 1 11. + 3 3 12. + 1 9 9 2 4 5 5 8 1 -4 4
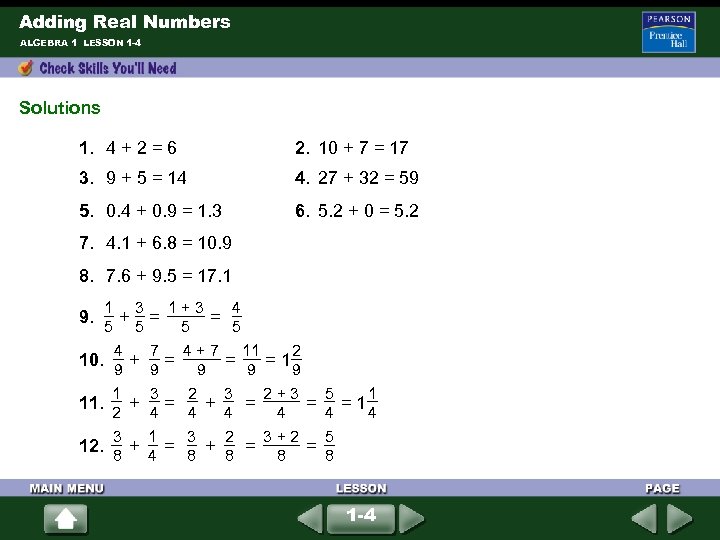
Adding Real Numbers ALGEBRA 1 LESSON 1 -4 Solutions 1. 4 + 2 = 6 2. 10 + 7 = 17 3. 9 + 5 = 14 4. 27 + 32 = 59 5. 0. 4 + 0. 9 = 1. 3 6. 5. 2 + 0 = 5. 2 7. 4. 1 + 6. 8 = 10. 9 8. 7. 6 + 9. 5 = 17. 1 1 5 3 5 1 + 3 4 5 5 2 4 7 4 + 7 11 10. + = = = 1 9 9 9 1 3 2 + 3 5 1 11. + = = = 1 2 4 4 4 3 1 3 2 3 + 2 5 12. + = = 8 8 4 8 8 8 9. + = 1 -4

Adding Real Numbers ALGEBRA 1 LESSON 1 -4 Use a number line to simplify each expression. a. 3 + (– 5) b. – 3 + 5 Start at 3. Start at – 3. Move left 5 units. Move right 5 units. 3 + (– 5) = – 2 – 3 + 5 = 2 c. – 3 + (– 5) Start at – 3. Move left 5 units. – 3 + (– 5) = – 8 1 -4
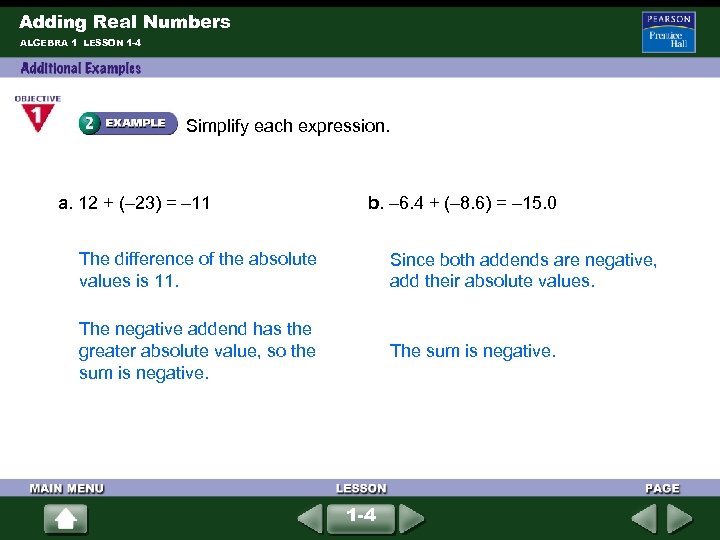
Adding Real Numbers ALGEBRA 1 LESSON 1 -4 Simplify each expression. a. 12 + (– 23) = – 11 b. – 6. 4 + (– 8. 6) = – 15. 0 The difference of the absolute values is 11. Since both addends are negative, add their absolute values. The negative addend has the greater absolute value, so the sum is negative. The sum is negative. 1 -4

Adding Real Numbers ALGEBRA 1 LESSON 1 -4 The water level in a lake rose 6 inches and then fell 11 inches. Write an addition statement to find the total change in water level. 6 + (– 11) = – 5 The water level fell 5 inches. 1 -4
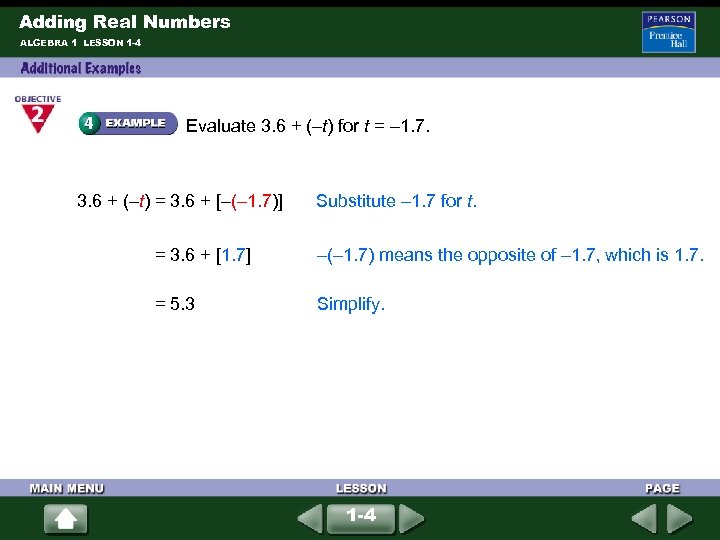
Adding Real Numbers ALGEBRA 1 LESSON 1 -4 Evaluate 3. 6 + (–t) for t = – 1. 7. 3. 6 + (–t) = 3. 6 + [–(– 1. 7)] Substitute – 1. 7 for t. = 3. 6 + [1. 7] –(– 1. 7) means the opposite of – 1. 7, which is 1. 7. = 5. 3 Simplify. 1 -4

Adding Real Numbers ALGEBRA 1 LESSON 1 -4 A scuba diver who is 88 ft below sea level begins to ascend to the surface. a. Write an expression to represent the diver’s depth below sea level after rising any number of feet. Relate: 88 ft below sea level plus feet diver rises Define: Let r = the number of feet the diver rises. Write: – 88 + r b. Find the new depth of the scuba diver after rising 37 ft. – 88 + r = – 88 + 37 Substitute 37 for r. = – 51 Simplify. The scuba diver is 51 ft below sea level. 1 -4

Adding Real Numbers ALGEBRA 1 LESSON 1 -4 = 1 13. 4 3. 2 8 11 2. 3 5 – 3 8. 6 11 2. 3 – 6 + 7 = 2. 3 + 11. 1 8. 6 – 6 Add – 6 5 – 3 8. 6 + (– 5. 4) 5 + 3 + + 11 + (– 2) – 3 + (– 1) 9 – 4 7 – 5. 4 – 2 11. 1 3 – 1 Add corresponding elements. Simplify. 1 -4

Adding Real Numbers ALGEBRA 1 LESSON 1 -4 pages 27– 30 Exercises 1 6 24. – 13 14 1. 6 + (– 3); 3 12. – 42 2. – 1 + (– 2); – 3 13. 2. 2 3. – 5 + 7; 2 14. – 0. 65 4. 3 + (– 4); – 1 15. – 7. 49 25. – 47 + 12 = – 35, 35 ft below the surface 5. 15 16. 1. 33 26. 8 + (– 5) = 3, 3 yd gain 6. – 11 17. 14 15 18. – 8 9 19. 6 3 16 1 20. – 6 8 27. – 6 + 13 = 7, 7°F 7. – 19 8. 12. 14 9. – 4 10. 5 11. – 8 23. 5 28. 8. 7 29. – 1. 7 30. 1. 7 31. – 8. 7 21. 0 32. 12. 6 22. – 13 18 1 -4
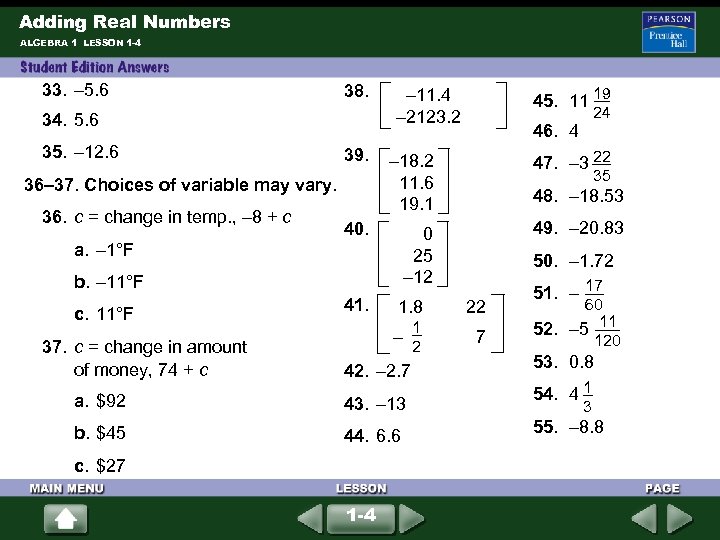
Adding Real Numbers ALGEBRA 1 LESSON 1 -4 33. – 5. 6 38. 34. 5. 6 35. – 12. 6 39. 36– 37. Choices of variable may vary. 36. c = change in temp. , – 8 + c 40. 37. c = change in amount of money, 74 + c 41. 1. 8 1 – 2 42. – 2. 7 a. $92 43. – 13 b. $45 44. 6. 6 c. $27 1 -4 47. – 3 22 35 48. – 18. 53 49. – 20. 83 0 25 – 12 b. – 11°F 24 46. 4 – 18. 2 11. 6 19. 1 a. – 1°F c. 11°F 45. 11 19 – 11. 4 – 2123. 2 50. – 1. 72 22 7 51. – 17 60 52. – 5 11 120 53. 0. 8 54. 4 1 3 55. – 8. 8

Adding Real Numbers ALGEBRA 1 LESSON 1 -4 56. 13. 8 million people 65. 5 72. – 0. 6 57. 6. 3 million people 66. – 1 73. 8. 7 58. Weaving; add the numbers in each column. 67. 1 74. 0. 1 68. The sum of – 227 and 319; the sum of – 227 and 319 is positive, while the sum of 227 and – 319 is negative. 75. – 1. 9 100 50 59. a. = 442 221 b. 0. 23 c. about 23% 62. 1 69. Answers may vary. Sample: Although 20 and – 20 are opposite numbers, there is no such thing as opposite temperatures. 63. – 5 70. – 0. 3 64. 7 71. – 13. 7 60. 0 61. – 2 1 -4 76. +2

Adding Real Numbers ALGEBRA 1 LESSON 1 -4 77. Answers may vary. Sample: 80. (continued) b. 13 2 0 1 5 – 1 3 0. 5 18 4 6 78. The matrices are not the same size, so they can’t be added. 79. No; time and temperature are different quantities and can’t be added. 80. a. 8 10 4 3 2 1 51 21 01 5 8 2 2 2 1 11 01 01 2 82. a. 4 62 22 02 c. 4 employees d. 10 employees e. Answers may vary. Sample: Multiply the entries in each column by the appropriate hourly wage, then by 8, and then add all entries to find the total wages. f. $3230 81. $7 1 -4 b. – 4

Adding Real Numbers ALGEBRA 1 LESSON 1 -4 83. 90. – x 1 1 1 – 1 2 4 21 1 2 84. 81 32 2 20 10 86. – c 2 87. 58 a 21 88. – 2 b 9 89. x 12 – 27 1 2 0 6 85. w 91. t 96. Pos. ; if m is neg. , –m is pos. and the sum of two pos. is pos. 12 6 92. – 3 m + 1 4 93. m 9 97. Zero; sum of neg. and pos. is the difference of the 94. Pos. ; if m is neg. , abs. values. –m is pos. and the |n| = |m| so |n| – |m| = 0. sum of two pos. is pos. 98. zero; n + (–m) = n + (–n) = 0 95. Neg. ; if n is pos. , 103. C 107. < 111. 9 –n is neg. and the 99. B sum of two neg. 100. F 104. H 108. > 112. 2. 2 is neg. 101. D 105. < 109. > 113. 18 102. F 1 -4 106. = 110. = 114. 21

Adding Real Numbers ALGEBRA 1 LESSON 1 -4 Simplify. 1. 15 + (– 10) 5 4 1 4. – 1 + (– 3 ) 5 – 4 7 15 15 2. – 57 + (– 11) – 68 5. 3 – 5 – 2 0 6. Evaluate 25 + 4 x for x = – 5. 5 1 -4 + 3. – 42 + 19 – 23 – 2 – 4 8 – 6 1 6 – 9 – 6

Subtracting Real Numbers ALGEBRA 1 LESSON 1 -5 (For help, go to Lessons 1 -3 and 1 -4) Find the opposite of each number. 1. 6 2. – 7 3. 3. 79 4. – 7 Simplify. 5. 3 + (– 2) 6. 9. 5 + (– 3. 5) 7. 13 + (– 8) 8. + – ( 6 ) 1 -5 19 2 3 1
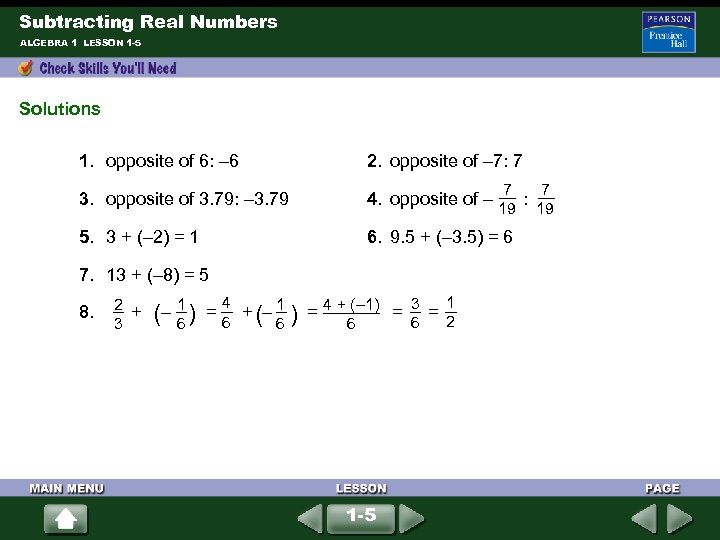
Subtracting Real Numbers ALGEBRA 1 LESSON 1 -5 Solutions 1. opposite of 6: – 6 2. opposite of – 7: 7 3. opposite of 3. 79: – 3. 79 4. opposite of – : 5. 3 + (– 2) = 1 6. 9. 5 + (– 3. 5) = 6 7 19 7. 13 + (– 8) = 5 6 6 1 4 3 1 2 8. + – = + – = = ( 1 ) ( ) 4 + (– 1) 3 6 6 1 -5 6 2 7 19
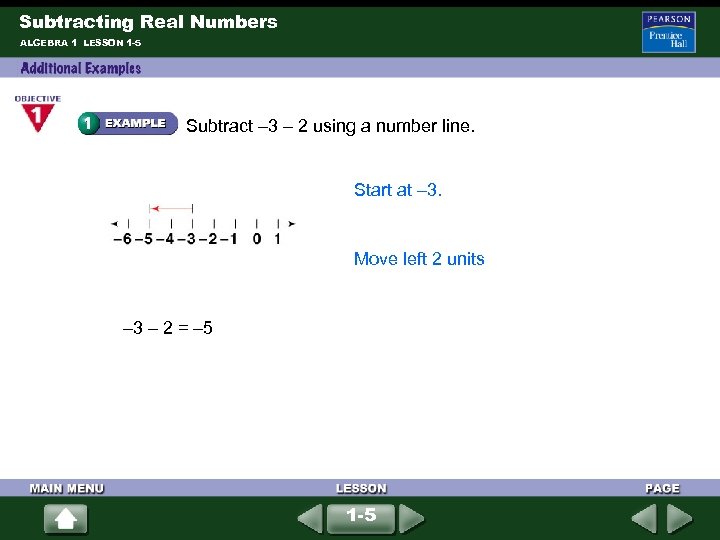
Subtracting Real Numbers ALGEBRA 1 LESSON 1 -5 Subtract – 3 – 2 using a number line. Start at – 3. Move left 2 units – 3 – 2 = – 5 1 -5
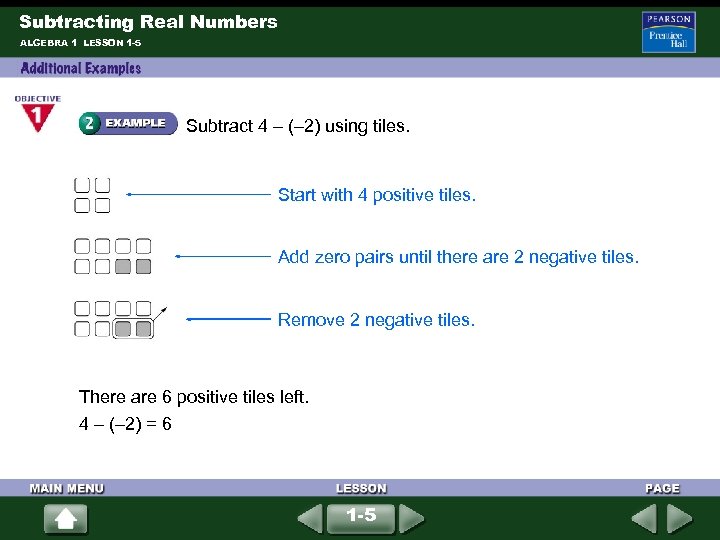
Subtracting Real Numbers ALGEBRA 1 LESSON 1 -5 Subtract 4 – (– 2) using tiles. Start with 4 positive tiles. Add zero pairs until there are 2 negative tiles. Remove 2 negative tiles. There are 6 positive tiles left. 4 – (– 2) = 6 1 -5
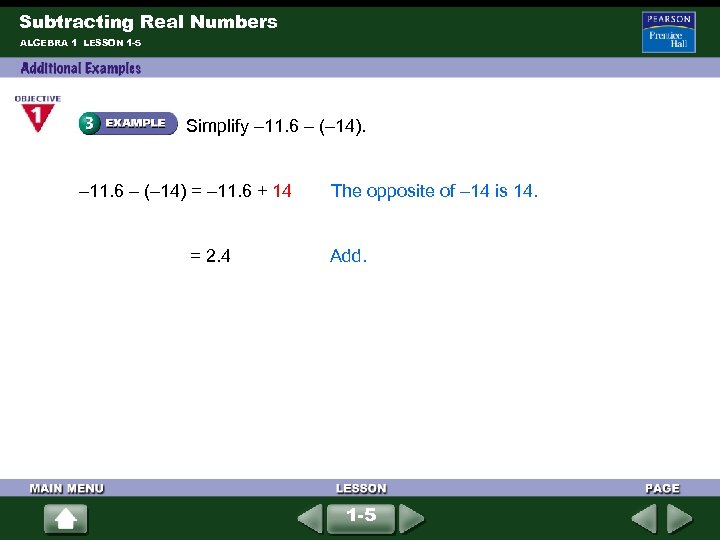
Subtracting Real Numbers ALGEBRA 1 LESSON 1 -5 Simplify – 11. 6 – (– 14) = – 11. 6 + 14 = 2. 4 The opposite of – 14 is 14. Add. 1 -5
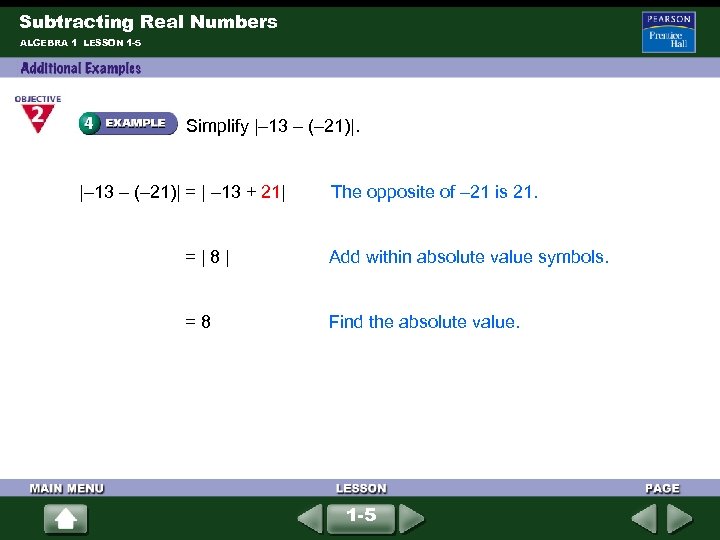
Subtracting Real Numbers ALGEBRA 1 LESSON 1 -5 Simplify |– 13 – (– 21)| = | – 13 + 21| The opposite of – 21 is 21. = | 8 | Add within absolute value symbols. = 8 Find the absolute value. 1 -5
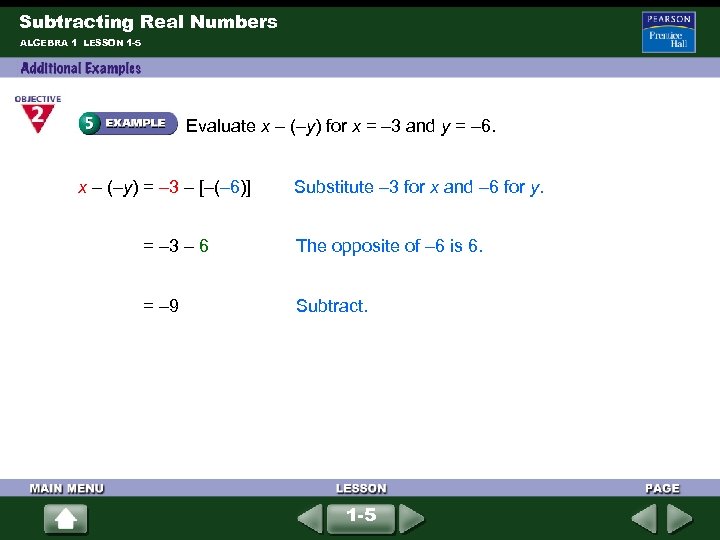
Subtracting Real Numbers ALGEBRA 1 LESSON 1 -5 Evaluate x – (–y) for x = – 3 and y = – 6. x – (–y) = – 3 – [–(– 6)] Substitute – 3 for x and – 6 for y. = – 3 – 6 The opposite of – 6 is 6. = – 9 Subtract. 1 -5
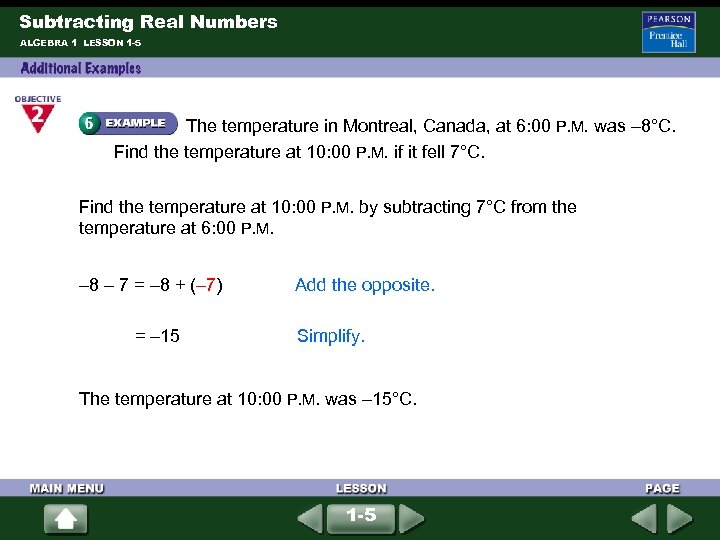
Subtracting Real Numbers ALGEBRA 1 LESSON 1 -5 The temperature in Montreal, Canada, at 6: 00 P. M. was – 8°C. Find the temperature at 10: 00 P. M. if it fell 7°C. Find the temperature at 10: 00 P. M. by subtracting 7°C from the temperature at 6: 00 P. M. – 8 – 7 = – 8 + (– 7) = – 15 Add the opposite. Simplify. The temperature at 10: 00 P. M. was – 15°C. 1 -5
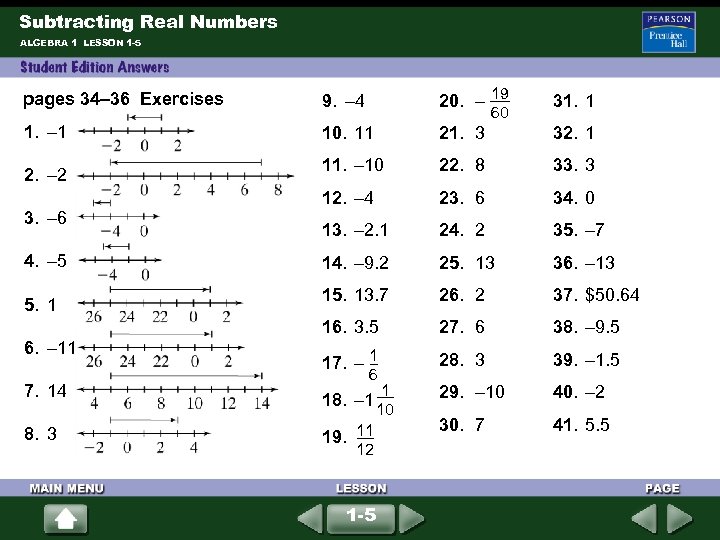
Subtracting Real Numbers ALGEBRA 1 LESSON 1 -5 pages 34– 36 Exercises 9. – 4 20. – 19 31. 1 1. – 1 10. 11 21. 3 32. 1 11. – 10 22. 8 33. 3 12. – 4 23. 6 34. 0 13. – 2. 1 24. 2 35. – 7 14. – 9. 2 25. 13 36. – 13 15. 13. 7 26. 2 37. $50. 64 16. 3. 5 27. 6 38. – 9. 5 17. – 1 28. 3 39. – 1. 5 29. – 10 40. – 2 30. 7 41. 5. 5 2. – 2 3. – 6 4. – 5 5. 1 6. – 11 7. 14 8. 3 6 1 18. – 1 10 19. 11 12 1 -5 60

Subtracting Real Numbers ALGEBRA 1 LESSON 1 -5 42. 1. 5 52. false; – 1 – (– 7) = 6, – 1 + (– 7) = – 8 43. – 1 53. false; 2 – (– 1) = 3, 3 < 2 or – 1 44. 16 54. true 45. – 16 55. a. 1992: 5. 5 1. 4 4. 2 1. 6 46. 11 47. 1 48. – 2 49. 12. 5 1997: 8. 2 3. 8 5. 2 4. 9 3. 9 1. 3 5. 1 7. 9 1. 8 4. 1 4. 9 1. 7 1. 3 2. 9 1. 3 – 0. 3 0 – 0. 4 – 1. 4 – 2. 2 1. 4 0. 3 0 0. 2 – 0. 3 – 2. 2 c. Answers may vary. Sample: Invest in soccer; it is the only sport that has not lost any participants. 50. 650 ft 51. Answers may vary. Sample: 5 12 – 3 7 6. 8 1. 0 5. 6 1. 8 b. – 4 6 5 10 = 1 6 – 8 – 3 1 -5

Subtracting Real Numbers ALGEBRA 1 LESSON 1 -5 56. 2 – 9 3 62. – 4 x + 9 73. – 9 63. – 12 t – m 1 57. [– 0 – 3] 64. 29 r – 35 74. – 0. 7 16 65. – 15 w – 8 9 4 58. 1 5 – 12 66. |x| – |y|, |x – y| – 1 60. – 9 20 61. 37 60 76. 4 0 0 16 68. F 77. 1. 2 – 2. 5 5. 2 69. C 59. a. Yes, answers may vary. Sample: n and –n always have the same absolute value. b. No, answers may vary. Sample: |1| + | – 1| | 1 + (– 1)|, 2 0 = / and x – y, |x + y| 75. – 4. 1 78. 67. C 70. H 71. D 72. 4 1 -5 1 – 3 2 1 3 2 – 3 6 – 4 1 3

Subtracting Real Numbers ALGEBRA 1 LESSON 1 -5 79– 81. Choices of variables may vary. 79. t = total cost, p = pounds of pears, t = 1. 19 p 80. p = bouquet’s price, m = money left, m = 20 – p 81. c = check ($), c s = your share, s = 6 1 -5

Subtracting Real Numbers ALGEBRA 1 LESSON 1 -5 Simplify each expression. 1. 7 – 12 – 5 2. 3 – (– 8) 11 3. – 7 – 5 – 12 Evaluate each expression for x = 3 and y = 4. 4. x – y – 1 5. | – y – x| 7 6. – 2 y x 4 – 5 9 0 1 -5 – x – 5 8 y
Multiplying and Dividing Real Numbers ALGEBRA 1 LESSON 1 -6 (For help, go to Lessons 1 -4 and 1 -5. ) Simplify each expression. 1. – 2 + (– 2) 2. – 5 + (– 5) 3. – 6 – 6 4. – 12 – 12 Write the next three numbers in each pattern. 5. 2, 4, 6, , , 6. 6, 4, 2, , , 7. 12, 9, 6, , , 8. – 18, – 12, – 6, , , 1 -6
Multiplying and Dividing Real Numbers ALGEBRA 1 LESSON 1 -6 Solutions 1. – 2 + (– 2) = 4(– 2) = – 8 2. – 5 + (– 5) = 5(– 5) = – 25 3. – 6 – 6 = 4(– 6) = – 24 4. – 12 – 12 = 6(– 12) = – 72 5. 4 – 2 = 2, and 6 – 4 = 2, so the pattern is to add 2: 6 + 2 = 8, 8 + 2 = 10, and 10 + 2 = 12. 2, 4, 6, 8, 10, 12 6. 4 – 6 = – 2, and 2 – 4 = – 2, so the pattern is to subtract 2: 2 – 2 = 0, 0 – 2 = – 2, and – 2 = – 4. 6, 4, 2, 0, – 2, – 4 7. 9 – 12 = – 3, and 6 – 9 = – 3, so the pattern is to subtract 3: 6 – 3 = 3, 3 – 3 = 0, and 0 – 3 = – 3. 12, 9, 6, 3, 0, – 3 8. – 12 – (– 18) = 6, and – 6 – (– 12) = 6, so the pattern is to add 6: – 6 + 6 = 0, 0 + 6 = 6, and 6 + 6 = 12. – 18, – 12, – 6, 0, 6, 12 1 -6
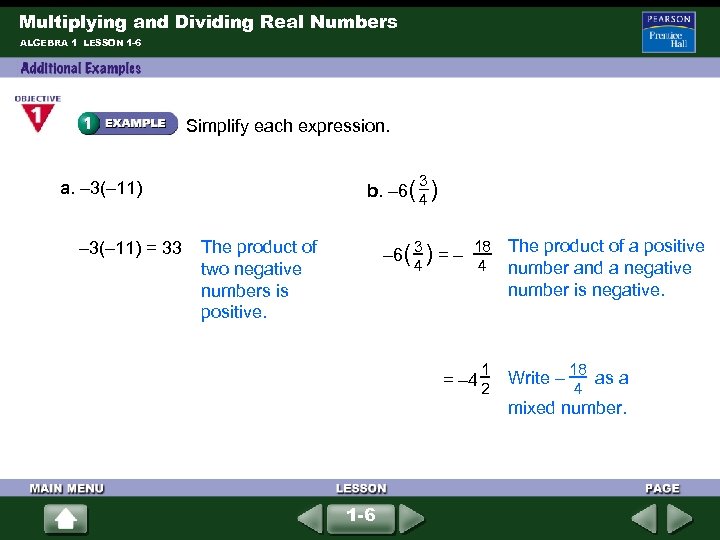
Multiplying and Dividing Real Numbers ALGEBRA 1 LESSON 1 -6 Simplify each expression. 3 b. – 6( 4 ) a. – 3(– 11) = 33 – 6( 3 ) = – 18 The product of a positive 4 4 number and a negative number is negative. The product of two negative numbers is positive. 1 = – 4 2 1 -6 18 Write – as a 4 mixed number.
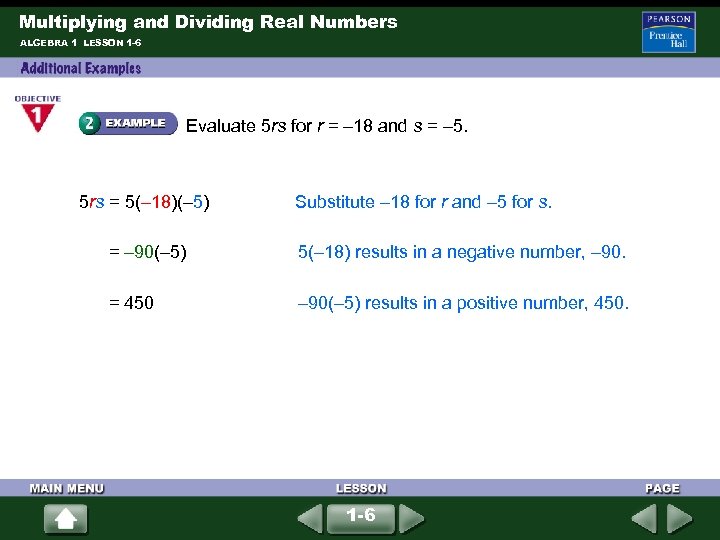
Multiplying and Dividing Real Numbers ALGEBRA 1 LESSON 1 -6 Evaluate 5 rs for r = – 18 and s = – 5. 5 rs = 5(– 18)(– 5) Substitute – 18 for r and – 5 for s. = – 90(– 5) 5(– 18) results in a negative number, – 90. = 450 – 90(– 5) results in a positive number, 450. 1 -6
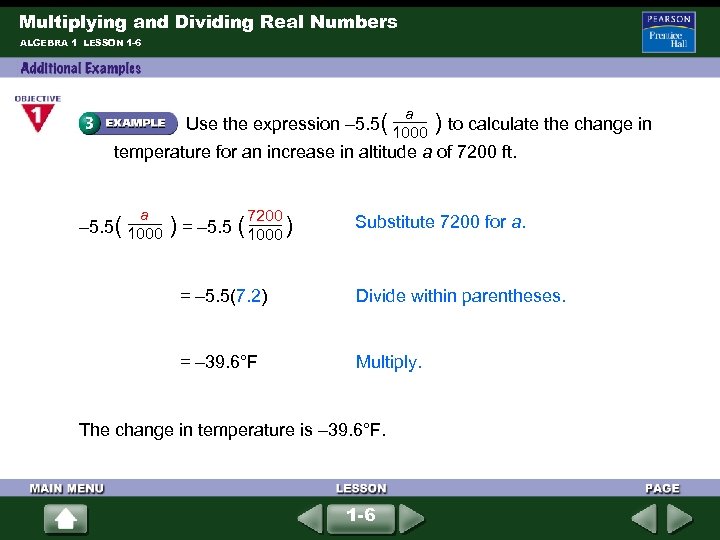
Multiplying and Dividing Real Numbers ALGEBRA 1 LESSON 1 -6 a Use the expression – 5. 5( ) to calculate the change in 1000 temperature for an increase in altitude a of 7200 ft. a 7200 – 5. 5( ) = – 5. 5 ( ) 1000 Substitute 7200 for a. = – 5. 5(7. 2) Divide within parentheses. = – 39. 6°F Multiply. The change in temperature is – 39. 6°F. 1 -6
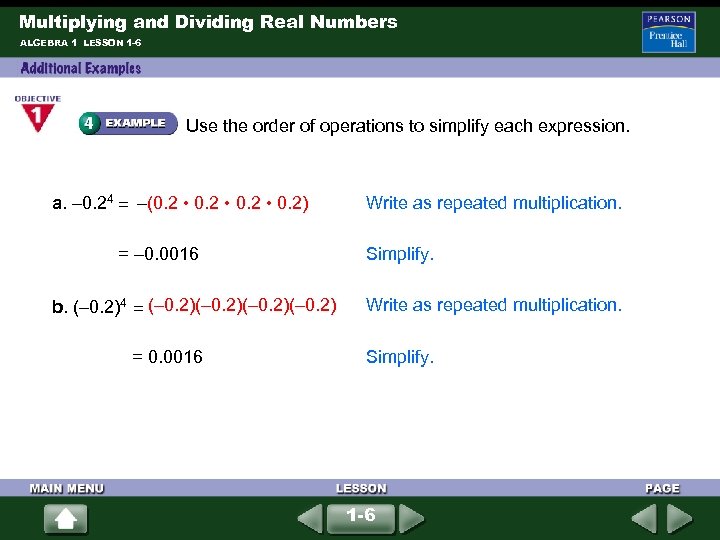
Multiplying and Dividing Real Numbers ALGEBRA 1 LESSON 1 -6 Use the order of operations to simplify each expression. a. – 0. 24 = –(0. 2 • 0. 2) = – 0. 0016 b. (– 0. 2)4 = (– 0. 2)(– 0. 2) = 0. 0016 Write as repeated multiplication. Simplify. 1 -6
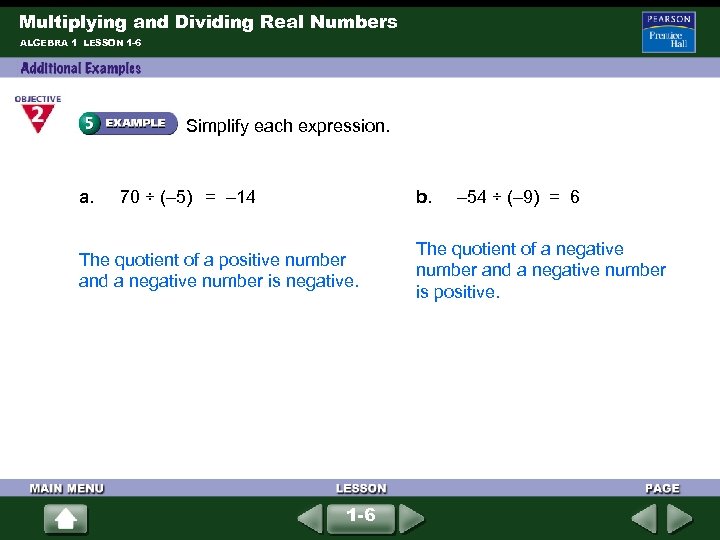
Multiplying and Dividing Real Numbers ALGEBRA 1 LESSON 1 -6 Simplify each expression. a. 70 ÷ (– 5) = – 14 b. The quotient of a positive number and a negative number is negative. 1 -6 – 54 ÷ (– 9) = 6 The quotient of a negative number and a negative number is positive.
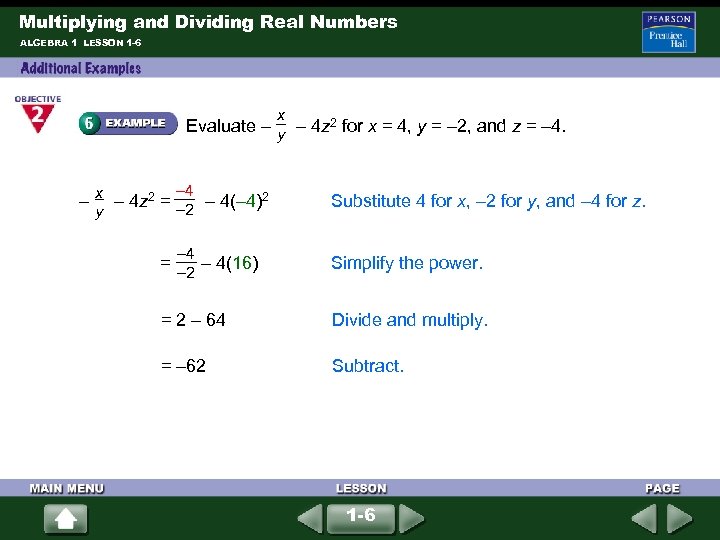
Multiplying and Dividing Real Numbers ALGEBRA 1 LESSON 1 -6 x Evaluate – – 4 z 2 for x = 4, y = – 2, and z = – 4. y – 4 x – – 4 z 2 = – 4(– 4)2 – 2 y – 4 Substitute 4 for x, – 2 for y, and – 4 for z. = – 4(16) – 2 Simplify the power. = 2 – 64 Divide and multiply. = – 62 Subtract. 1 -6
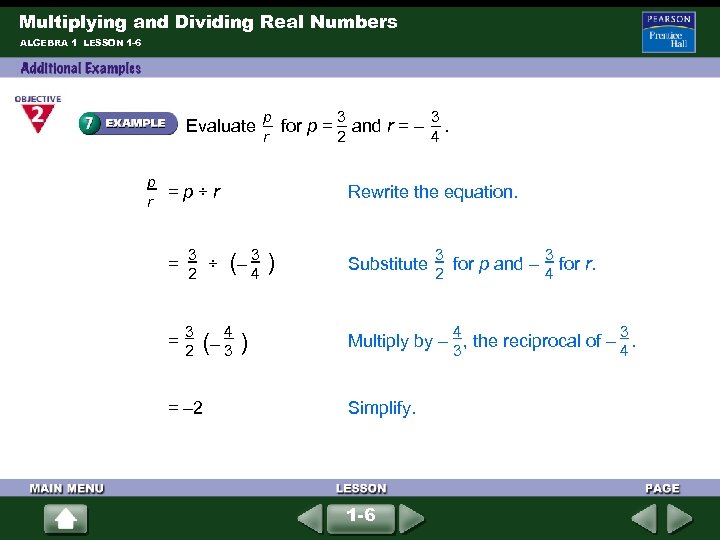
Multiplying and Dividing Real Numbers ALGEBRA 1 LESSON 1 -6 p r 3 2 3 4 Evaluate for p = and r = – . p = p ÷ r r Rewrite the equation. 3 3 = ÷ (– ) 4 2 3 4 3 3 Substitute for p and – for r. 2 4 4 3 = 2 (– ) 3 Multiply by – , the reciprocal of – . 3 4 = – 2 Simplify. 1 -6
Multiplying and Dividing Real Numbers ALGEBRA 1 LESSON 1 -6 pages 41– 44 Exercises 23. – 432 33. 8 45. 12 4 5 1. – 15 12. 81 24. 1 34. – 25 46. – 2 2. – 15 13. – 12 25. – 64 35. 81 47. – 8 3. 15 14. 12 26. – 87 36. – 81 48. – 1 4. 15 15. – 15 27. 4 37. – 192 49. – 7 5. – 34. 4 16. 5 28. 24 38. – 5 50. – 28 17. – 8 29. 36 39. 675 51. 0 7. – 120 18. – 13 30. 12 40. – 2 52. 4 2 8. – 105 19. 48 41. – 4 9. – 80 20. 1 10. 80 21. 12 31. a. – 24°F b. – 75°F c. – 51°F d. – 31. 5°F 11. – 78 22. – 8 32. – 1 44. – 11 6. – 2 1 -6 42. 5 1 2 43. 6 3 1 53. 3 2 54. 1 1 3 55. – 15 1 2

Multiplying and Dividing Real Numbers ALGEBRA 1 LESSON 1 -6 56. 1 18 57. – 6 25 58. – 2 68. – 60 69. 30 70. a. i. 2 59. 18 ii. – 6 60. – 1 71. a. When a and b are both neg. or both pos. b. When a is neg. and b is pos. , or when a is pos. and b is neg. iii. 24 2 61. – 8 15 62. – 125 63. 0. 75 64. – 27 65. 22. 32 66. 44 67. – 27 5 12 73. – 5 6 74. 1 7 8 75. – 1 5 72. – 1 iv. – 120 b. pos. c. neg. d. No; answers may vary. Sample: The sign of the product is not affected by the number of pos. factors, only by the number of neg. factors. 1 -6 76. – 6 1 2 78. – 1 10 79. 1 5 77. – 4

Multiplying and Dividing Real Numbers ALGEBRA 1 LESSON 1 -6 80– 84. Answers may vary. 87. a. 4, – 8, 16, – 32 Samples are given. 9, – 27, 81, – 243 80. ac + b 81. b – a + c 82. ab – c 83. –ab + c 84. –bc + a b. Pos. ; the expression will involve an even number of neg. factors. c. Neg. ; the expression will involve an odd number of neg. factors. 90. – 22 10 18 – 12 8 – 6 91. – 15 21 2 – 9 3 92. 4. 7 – 1. 3 – 0. 02 6. 4 2 93. [– 12 – 2 ] 3 88. 0. 1 is the multiplicative 85. 31¢ 94. – 8 – 10. 6 inverse of 10 because 86. Yes; whatever the 6. 2 0 0. 1(10) = 1. (– 10 is the signs of a and b, | ab |, opposite of 10. ) 95. | a |, and | b | are pos. , 1 – 1 3 89. The opposite of a nonzero and | ab | = | a | • | b |. 4 16 2 number n is –n while the 9 0 1 multiplicative inverse is . n 1 -6 0. 79 0 4 12

Multiplying and Dividing Real Numbers ALGEBRA 1 LESSON 1 -6 96. a. 139 ft; 91 ft 102. 1 114. – 2 = – 101, so h = 0 for some value less than 4 (about 3. 1). 97. a. a = 5000 – 25 t b. 312. 5 ft c. 4687. 5 ft 104. – 8 105. , or 11 4 4 106. – 9 16 107. – 5 48 108. 1 2 127. $34. 93 116. 0. 8 1 45 126. 196 115. – 20 64 b. Less than 4 s; 103. – 1 64 for t = 4, h = 155 – 16 t 2 117. 9. 8 1 118. 2 4 119. 1 72 120. 4. 95 98. – 23°C 109. A 121. 56 99. – 1 8 100. 1 16 101. – 1 32 110. F 122. 4. 59 111. C 112. H 123. 4 124. 23 113. B 125. 121 3 1 -6

Multiplying and Dividing Real Numbers ALGEBRA 1 LESSON 1 -6 Simplify. 1. – 8(– 7) 56 2. – 6(– 7 + 10) – 4 – 22 Evaluate each expression for m = – 3, n = 4, and p = – 1. 8 m n 3. + p – 7 4. (mp)3 5. mnp 27 12 1 3 1 6. Evaluate 2 a ÷ 4 b – c for a = – 2, b = – , and c = – . 2 1 32 1 -6
The Distributive Property ALGEBRA 1 LESSON 1 -7 (For help, go to Lessons 1 -2 and 1 -6. ) Use the order of operations to simplify each expression. 1. 3(4 + 7) 2. – 2(5 + 6) 4. – 0. 5(8 – 6) 5. t(10 – 4) 1 2 1 -7 3. – 1(– 9 + 8) 6. m(– 3 – 1)
The Distributive Property ALGEBRA 1 LESSON 1 -7 Solutions 1. 3(4 + 7) = 3(11) = 33 2. – 2(5 + 6) = – 2(11) = – 22 3. – 1(– 9 + 8) = – 1(– 1) = 1 4. – 0. 5(8 – 6) = – 0. 5(2) = – 1 1 1 5. t(10 – 4) = t(6) = (6)t = • 6 t = 3 t ( ) 2 2 6. m(– 3 – 1) = m(– 4) = – 4 m 1 -7
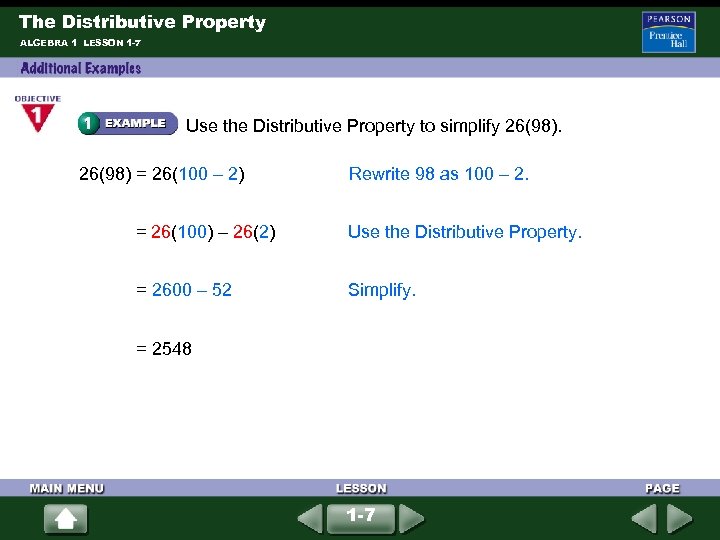
The Distributive Property ALGEBRA 1 LESSON 1 -7 Use the Distributive Property to simplify 26(98) = 26(100 – 2) Rewrite 98 as 100 – 2. = 26(100) – 26(2) Use the Distributive Property. = 2600 – 52 Simplify. = 2548 1 -7
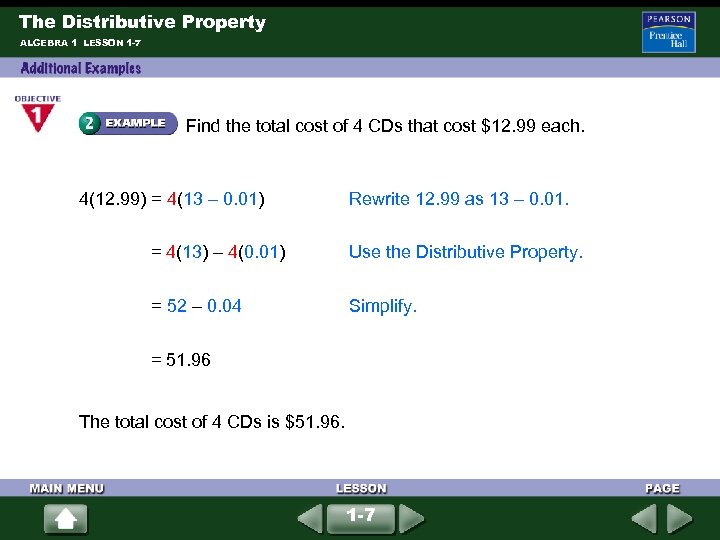
The Distributive Property ALGEBRA 1 LESSON 1 -7 Find the total cost of 4 CDs that cost $12. 99 each. 4(12. 99) = 4(13 – 0. 01) Rewrite 12. 99 as 13 – 0. 01. = 4(13) – 4(0. 01) Use the Distributive Property. = 52 – 0. 04 Simplify. = 51. 96 The total cost of 4 CDs is $51. 96. 1 -7
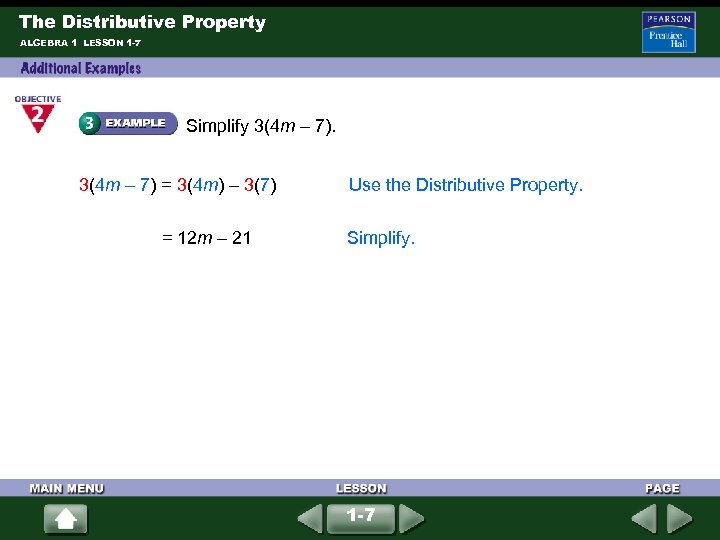
The Distributive Property ALGEBRA 1 LESSON 1 -7 Simplify 3(4 m – 7) = 3(4 m) – 3(7) = 12 m – 21 Use the Distributive Property. Simplify. 1 -7
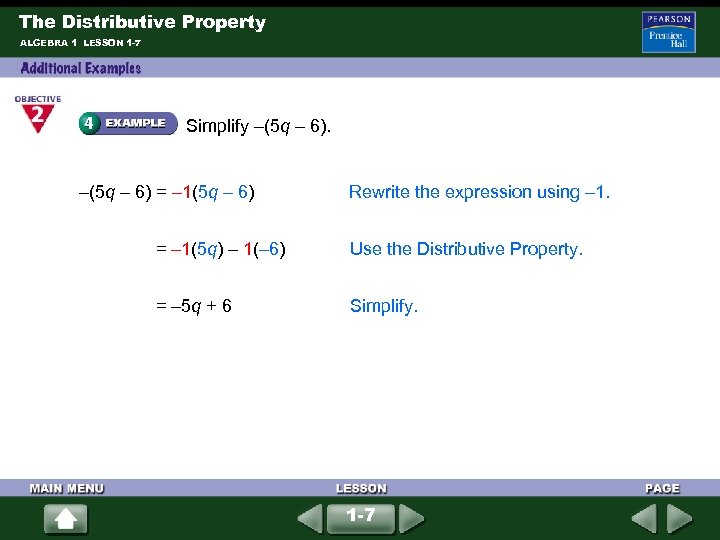
The Distributive Property ALGEBRA 1 LESSON 1 -7 Simplify –(5 q – 6) = – 1(5 q – 6) Rewrite the expression using – 1. = – 1(5 q) – 1(– 6) Use the Distributive Property. = – 5 q + 6 Simplify. 1 -7
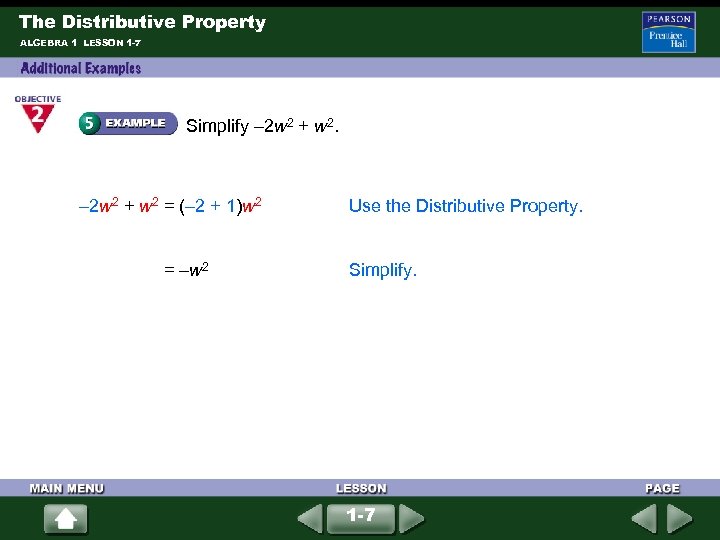
The Distributive Property ALGEBRA 1 LESSON 1 -7 Simplify – 2 w 2 + w 2 = (– 2 + 1)w 2 = –w 2 Use the Distributive Property. Simplify. 1 -7
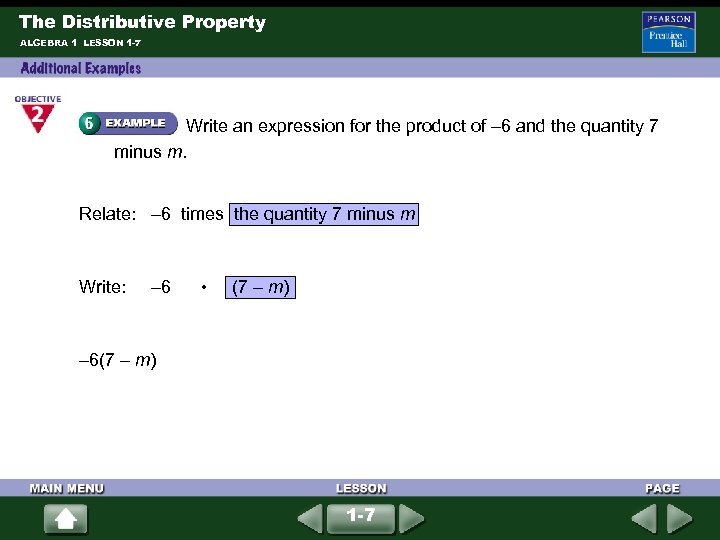
The Distributive Property ALGEBRA 1 LESSON 1 -7 Write an expression for the product of – 6 and the quantity 7 minus m. Relate: – 6 times the quantity 7 minus m Write: – 6 • (7 – m) – 6(7 – m) 1 -7
The Distributive Property ALGEBRA 1 LESSON 1 -7 pages 50– 52 Exercises 1. 2412 12. $209. 51 2. 663 13. $98. 97 3. 5489 14. $2. 76 4. 2448 15. 7 t – 28 5. 686 16. – 2 n + 12 6. 2997 17. 3 m + 12 7. 20, 582 18. b – 4 5 8. 24, 480 19. – 2 x – 6 9. $3. 96 20. 4 y + 6 10. $11. 82 21. 1. 5 q + 8 11. $29. 55 22. 18 n – 42 5 15 23. – r 35. – 3 t 24. – 4. 5 b + 13. 5 36. 20 k 2 25. 2 w + 4 37. 7 x 26. – 36 + 16 n 38. 24 w 27. –x – 3 39. 5 v 2 28. –x + 3 40. 6 m 29. – 3 – x 41. – 17 q 30. – 3 + x 42. – 45 x 31. – 6 k – 5 43. 3(m – 7) 32. – 7 x + 2 44. – 4(4 + w) 33. – 2 + 7 x 45. 2(b + 9) 34. – 4 + z 46. – 11(n – 8) 2 1 -7 16

The Distributive Property ALGEBRA 1 LESSON 1 -7 47. 2(3 c + 9) 59. 18. 6 + 15 m 70. 8 x + 38 48. (3 + r )(r – 7) 5 60. d – 42 71. No; 2 a • 2 b = 4 ab. 49. 44, 982 61. – 8. 4 – 300 g + 512 h 50. 2392 62. – 12 k – 5 m + 62 51. 14. 021 63. 6 p – 14 q + 30 w 52. 84. 012 64. 36 x + 10. 8 y – 72. 9 72. The student did not mult. the second number in parentheses, 10, by 4 to get the correct answer, 12 x + 40. 53. 11. 82 65. 54. 15. 992 55. 30. 1 + 7 x 40 50 56. d – dh 7 8 7 57. 12. 8 – n 58. 135 b + 128 66. 67. 68. 69. 1 1 2 (5 – k) 4 2 7 4 6 (8 + p) 100 3 13 11 (b – ) 30 20 17 z – 34 1 11 4 (x – ) 3 12 1 -7 73. Answers may vary. Sample: 2(x + 5) = 2 x + 10 74. 4. 78 d 75. – 76 p 2 – 20 p – 9 76. – 6. 1 t 2 + 13. 7 t 77. 1. 5 m – 12. 5 v

The Distributive Property ALGEBRA 1 LESSON 1 -7 78. 71 n + n 3 42 3 107 79. – k + h 20 120 86. 10 pennies, 7 nickels, 80. 7 m 2 – mz + 4 87. 4(1. 02) + 3(0. 99) + 3(0. 52) 81. 19 – 7 t + 6 y 4 quarters, 1 dime = t ; $8. 61 82. 1. 4 b – 5 b 2 + 5 c 88. 27 + 3 t 83. – 4 xyz + 6 xy 89. – 6 r + 37 84. terms: – 7 t, 6 v, 7, – 19 y, 90. – 3 m – 9 coefficients: – 7, 6, – 19, 91. 2 a + 2 ab + abc constant: 7 85. a. (84 + 10)50 ft 2 b. 4700 ft 2 92. 14 b + 42 b 2 93. 5 y + 13 z 94. 3 x – 10 3 1 -7 95. a. 2; 2 b. – 2; – 2 c. Yes; the two expressions are equal for the values of a, b, and c in parts (a) and (b). 96. a. 30; – 8 b. 12, – 6 c. No; parts (a) and (b) show the expressions are not equal.

The Distributive Property ALGEBRA 1 LESSON 1 -7 97. D 109. 1 121. – 7. 7 98. G 110. – 5 122. 23 99. A 100. F 6 4 111. – 1 5 123. a. 4 + m 3 b. 7; 5; 8 112. – 3 101. D 113. – 17 102. H 114. – 2. 386 103. C 115. 127 104. I 116. 45. 3 105. – 68 117. 45. 7 106. – 4 118. 2. 57 107. 4 119. 0. 92 108. 7 120. – 9. 6 1 -7

The Distributive Property ALGEBRA 1 LESSON 1 -7 Simplify each expression. 1. 11(299) 3289 2. 4(x + 8) 3. – 3(2 y – 7) 4 x + 32 – 6 y + 21 4. –(6 + p) 5. 1. 3 a + 2 b – 4 c + 3. 1 b – 4 a – 6 – p – 2. 7 a + 5. 1 b – 4 c 4 7 3 5 6. Write an expression for the product of and the quantity b minus . 4 3 b – 5 ( ) 7 1 -7

Properties of Real Numbers ALGEBRA 1 LESSON 1 -8 (For help, go to Lessons 1 -4 and 1 -6. ) Simplify each expression. 1. 8 + (9 + 2) 2. 3 • (– 2 • 5) 3. 7 + 16 + 3 4. – 4(7)(– 5) 5. – 6 + 9 + (– 4) 6. 0. 25 • 3 • 4 7. 3 + x – 2 8. 2 t – 8 + 3 t 9. – 5 m + 2 m – 4 m 1 -8

Properties of Real Numbers ALGEBRA 1 LESSON 1 -8 Solutions 1. 8 + (9 + 2) = 8 + (2 + 9) = (8 + 2) + 9 = 10 + 9 = 19 2. 3 • (– 2 • 5) = 3 • (– 10) = – 30 3. 7 + 16 + 3 = 7 + 3 + 16 = 10 + 16 = 26 4. – 4(7)(– 5) = – 4(– 5)(7) = 20(7) = 140 5. – 6 + 9 + (– 4) = – 6 + (– 4) + 9 = – 10 + 9 = – 1 6. 0. 25 • 3 • 4 = 0. 25 • 4 • 3 = 1 • 3 = 3 7. 3 + x – 2 = 3 + (– 2) + x = 1 + x 8. 2 t – 8 + 3 t = 2 t + 3 t – 8 = (2 + 3)t – 8 = 5 t – 8 9. – 5 m + 2 m – 4 m = (– 5 + 2 – 4)m = – 7 m 1 -8

Properties of Real Numbers ALGEBRA 1 LESSON 1 -8 Name the property each equation illustrates. a. 3 • a = a • 3 Commutative Property of Multiplication, because the order of the factors changes b. p • 0 = 0 Multiplication Property of Zero, because a factor multiplied by zero is zero c. 6 + (– 6) = 0 Inverse Property of Addition, because the sum of a number and its inverse is zero 1 -8

Properties of Real Numbers ALGEBRA 1 LESSON 1 -8 Suppose you buy a shirt for $14. 85, a pair of pants for $21. 95, and a pair of shoes for $25. 15. Find the total amount you spent. 14. 85 + 21. 95 + 25. 15 = 14. 85 + 25. 15 + 21. 95 Commutative Property of Addition = (14. 85 + 25. 15) + 21. 95 Associative Property of Addition = 40. 00 + 21. 95 Add within parentheses first. = 61. 95 Simplify. The total amount spent was $61. 95. 1 -8
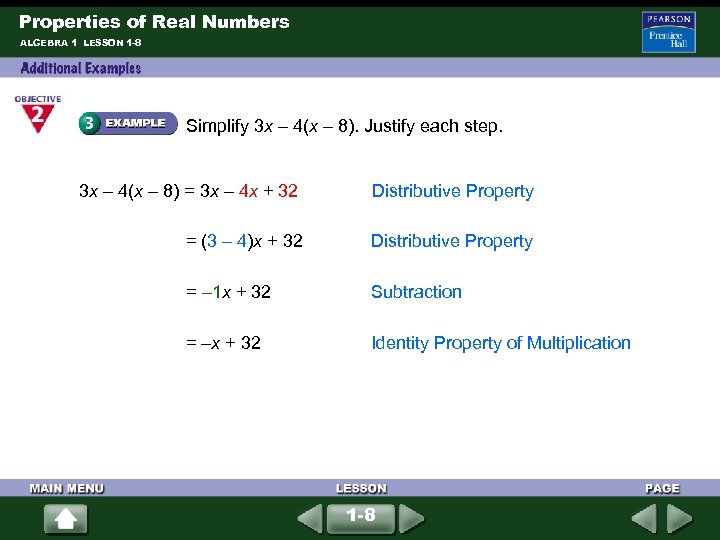
Properties of Real Numbers ALGEBRA 1 LESSON 1 -8 Simplify 3 x – 4(x – 8). Justify each step. 3 x – 4(x – 8) = 3 x – 4 x + 32 Distributive Property = (3 – 4)x + 32 Distributive Property = – 1 x + 32 Subtraction = –x + 32 Identity Property of Multiplication 1 -8

Properties of Real Numbers ALGEBRA 1 LESSON 1 -8 pages 56– 57 Exercises 5. Inv. Prop. of Add. ; a number and its 1. Ident. Prop. of Add. ; inverse are added. 0, the identity for addition, is added. 6. Comm. Prop. of Mult. ; 9. Inv. Prop. of Mult. ; a number and its mult. inverse are multiplied. 2. Comm. Prop. of Add. ; the order of the factors changes. the order of the terms changes. 7. Dist. Prop. ; a number 3. Ident. Prop. of Mult. ; outside parentheses is distributed to the 1, the identity for two terms inside multiplication, the parentheses. is multiplied. 10. 100 4. Assoc. Prop. of Add. ; 8. Assoc. Prop. of Mult. ; the grouping of the factors changes. terms changes. 1 -8 11. 7400 12. 14. 95 13. 4200 14. – 5 15. 13 16. $6. 00

Properties of Real Numbers ALGEBRA 1 LESSON 1 -8 17. a. def. of subtr. b. Dist. Prop. c. addition 20. – 5(7 y) = [– 5(7)]y Assoc. Prop. of Mult. = – 35 y mult. 23. 29 c + (– 29 c) = [29 + (– 29)]c Dist. Prop. = 0 • c Inv. Prop. of Add. = 0 Mult. Prop. of Zero 1 18. a. Comm. Prop. of Mult. 21. 8 + 9 m + 7 24. 43 + 1 = 1 + 1 43 = 9 m + 8 + 7 b. Assoc. Prop. of Mult. Inv. Prop. of Mult. Comm. Prop. of Add. = 2 add. c. mult. = 9 m + (8 + 7) 1 Assoc. Prop. of Add. 25. 2 + g = 2 + 1 d. mult. g = 9 m + 15 add. Inv. Prop. of Mult. 19. 25 • 1. 7 • 4 22. 12 x – 3 + 6 x = 3 add. = 25 • 4 • 1. 7 = 12 x + (– 3) + 6 x def. of subtr. Comm. Prop. of Mult. = 12 x + 6 x + (– 3) = (25 • 4) • 1. 7 Comm. Prop. of Add. Assoc. Prop. of Mult. = (12 + 6)x + (– 3) Dist. Prop. = 100 • 1. 7 mult. = 18 x + (– 3) add. = 170 mult. = 18 x – 3 def. of subtr. 1 -8

Properties of Real Numbers ALGEBRA 1 LESSON 1 -8 26. 36 jkm – 36 mjk 27. (32 – 23)(8759) 29. 4 + 6(8 – 3 m) = 36 jkm + (– 36)mjk = (9 – 8)(8759) mult. = 4 + 48 – 18 m def. of subtr. = [9 + (– 8)](8759) Dist. Prop. = 36 jkm + (– 36)jmk def. of subtr. = 4 + 48 + (– 18 m) Comm. Prop. of Mult. = 1(8759) add. def. of subtr. = 36 jkm + (– 36)jkm = 8759 = (4 + 48) + (– 18 m) Comm. Prop. of Mult. Ident. Prop. of Mult. Assoc. Prop. of Add. = [36 + (– 36)]jkm = 52 + (– 18 m) add. 28. (76 – 65)(8 – 8) Dist. Prop. = 52 – 18 m = (76 – 65)[8 + (– 8)] = (0)jkm Inv. def. of subtr. Prop. of Add. = (76 – 65) • 0 = 0 Inv. Prop. of Add. Mult. Prop. of Zero = 0 Mult. Prop. of Zero 1 -8

Properties of Real Numbers ALGEBRA 1 LESSON 1 -8 1 30. 5 w – – w(9) 5 1 = 5 w – – 9 w 5 Comm. Prop. of Mult. 1 = 5(w) – 5 – 9 w 31. 5 Dist. Prop. 32. = 5 w – 1 – 9 w 33. Inv. Prop. of Mult. = 5 w + (– 1) + (– 9 w) 34. def. of subtr. 35. = 5 w + (– 9 w) + (– 1) 36. Comm. Prop. of Add. = [5 w + (– 9 w)] + (– 1) 37. Assoc. Prop. of Add. 38. = – 4 w + (– 1) add. 40. No; 3 – 5 = – 2, while 5 – 3 = 2. = – 4 w – 1 41. No; (5 – 3) – 1 = 2 – 1 = 1, while def. of subtr. 5 – (3 – 1) = 5 – 2 = 3. 1 $52. 97 42. No; 1 ÷ 2 = , while 2 ÷ 1 = 2. 2 no no 43. No; 16 ÷ (4 ÷ 2) = 16 ÷ 2 = 8, while (16 ÷ 4) ÷ 2 = 4 ÷ 2 = 2. no 44. a. Dist. Prop. yes b. Comm. Prop. of Add. no c. Assoc. Prop. of Add. no d. add. yes e. Dist. Prop. f. add. = [5 + (– 9)]w + (– 1) 39. yes Dist. Prop. 1 -8

Properties of Real Numbers ALGEBRA 1 LESSON 1 -8 45. By the Comm. Prop. of Mult. , (b + c)a = a(b + c). By the Dist. Prop. , a(b + c) = ab + ac. By the Comm. Prop. of Mult. , ab + ac = ba + ca, so (b + c)a = ba + ca. 49. 50. 51. 52. 53. 54. 55. 46. Answers may vary. Sample: The sandwich tastes the same 56. whether the peanut butter or 57. the jelly is on top. This is like 58. the Comm. Prop. of Add. , 59. because you can add the 60. peanut butter and jelly in either order. 61. 62. 47. both 63. 48. both not mult. ; (– 2)(– 3) = 6 not add. ; 1 + 3 = 4 both A I D G B F 6 + 5 k 1 11 – b 3 – 10 p – 35 28 – 4 n 7. 4 m – 0. 05 1 -8 64. – 18 v + 31. 2 65. 7 + [m + (– 17)] 66. 8 – (9 – t) 1 b 2 4 1 68. (x + 5. 1) 3 67. ( ) 69. 7 70. – 18. 3 71. – 1 4 72. – 1 1 5 73. – 135 74. 9. 2

Properties of Real Numbers ALGEBRA 1 LESSON 1 -8 Name the property that each equation illustrates. 1. 1 m = m 2. (– 3 + 4) + 5 = – 3 + (4 + 5) Iden. Prop. Of Mult. 3. – 14 • 0 = 0 Assoc. Prop. Of Add. Mult. Prop. Of Zero 4. Give a reason to justify each step. a. 3 x – 2(x + 5) = 3 x – 2 x – 10 Distributive Property b. = 3 x + (– 2 x) + (– 10) Definition of Subtraction c. = [3 + (– 2)]x + (– 10) Distributive Property d. = 1 x + (– 10) Addition e. = 1 x – 10 Definition of Subtraction f. = x – 10 Identity Property of Multiplication 1 -8

Graphing Data on the Coordinate Plane ALGEBRA 1 LESSON 1 -9 (For help, go to Lesson 1 -3. ) Graph each number on a number line. 1. 6 2. – 5 3. 2. 7 4. 0 Write the coordinate of each point on the number line below. 5. A 6. B 7. C 1 -9 8. D

Graphing Data on the Coordinate Plane ALGEBRA 1 LESSON 1 -9 Solutions 1. 2. 3. 4. 5. A: 1 6. B: – 2. 5 7. C: 3. 5 1 -9 8. D: – 4
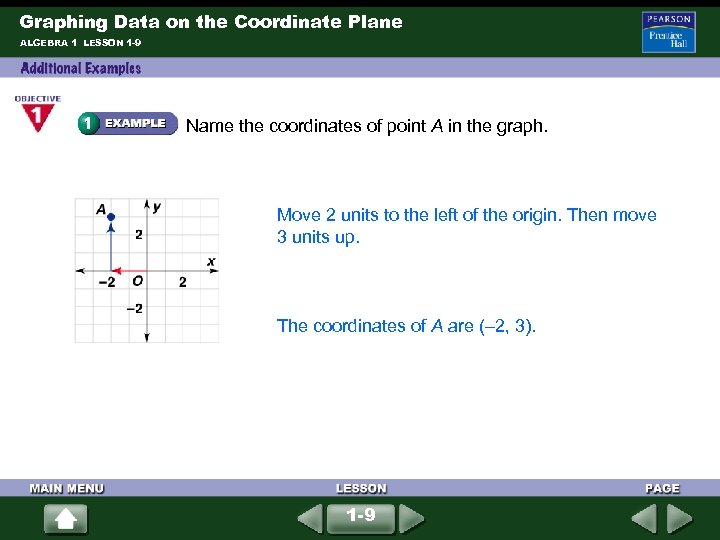
Graphing Data on the Coordinate Plane ALGEBRA 1 LESSON 1 -9 Name the coordinates of point A in the graph. Move 2 units to the left of the origin. Then move 3 units up. The coordinates of A are (– 2, 3). 1 -9
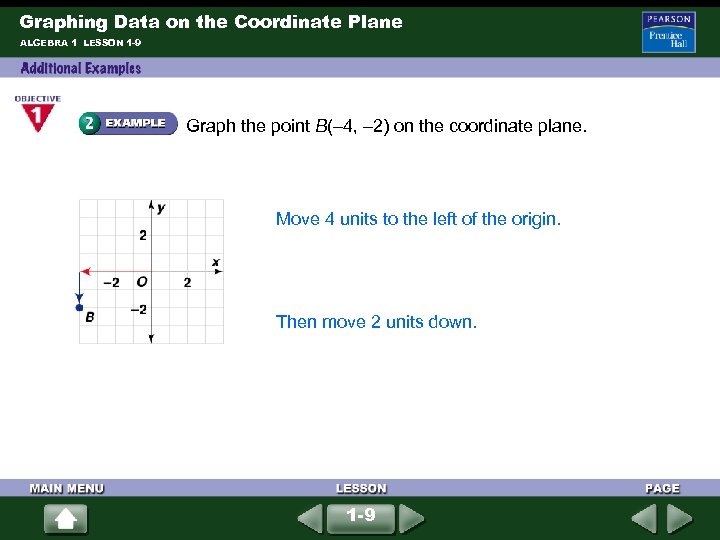
Graphing Data on the Coordinate Plane ALGEBRA 1 LESSON 1 -9 Graph the point B(– 4, – 2) on the coordinate plane. Move 4 units to the left of the origin. Then move 2 units down. 1 -9
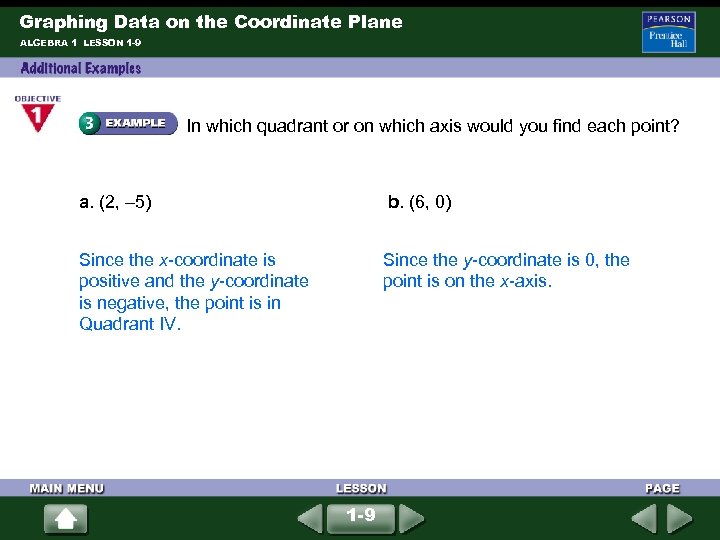
Graphing Data on the Coordinate Plane ALGEBRA 1 LESSON 1 -9 In which quadrant or on which axis would you find each point? a. (2, – 5) b. (6, 0) Since the x-coordinate is positive and the y-coordinate is negative, the point is in Quadrant IV. Since the y-coordinate is 0, the point is on the x-axis. 1 -9
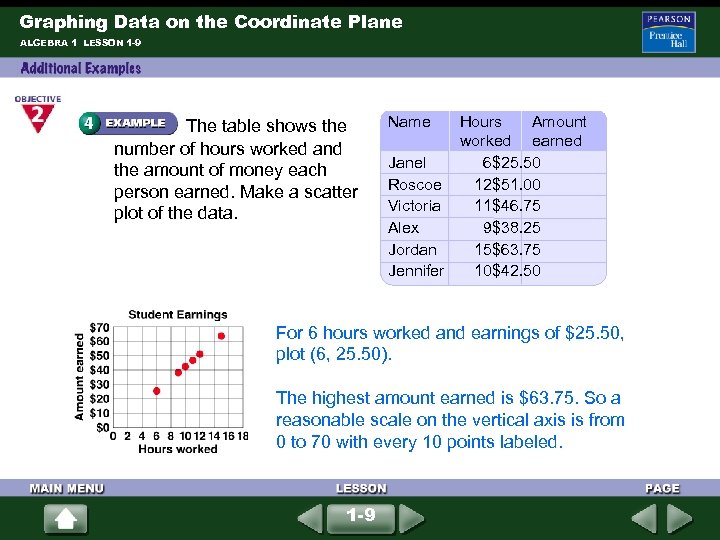
Graphing Data on the Coordinate Plane ALGEBRA 1 LESSON 1 -9 The table shows the number of hours worked and the amount of money each person earned. Make a scatter plot of the data. Name Hours Amount worked earned Janel 6$25. 50 Roscoe 12$51. 00 Victoria 11$46. 75 Alex 9$38. 25 Jordan 15$63. 75 Jennifer 10$42. 50 For 6 hours worked and earnings of $25. 50, plot (6, 25. 50). The highest amount earned is $63. 75. So a reasonable scale on the vertical axis is from 0 to 70 with every 10 points labeled. 1 -9
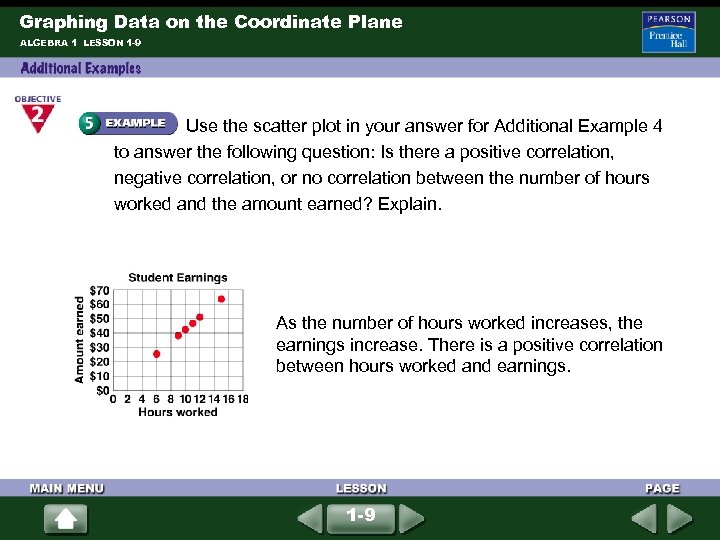
Graphing Data on the Coordinate Plane ALGEBRA 1 LESSON 1 -9 Use the scatter plot in your answer for Additional Example 4 to answer the following question: Is there a positive correlation, negative correlation, or no correlation between the number of hours worked and the amount earned? Explain. As the number of hours worked increases, the earnings increase. There is a positive correlation between hours worked and earnings. 1 -9
Graphing Data on the Coordinate Plane ALGEBRA 1 LESSON 1 -9 pages 62– 64 Exercises 11. IV 17. neg. correlation 1. (4, 5) 12. y–axis 2. (2, – 2) 13. I 3. (– 5, 0) 14. II 4. (5, 4) 15. No; the point is on the y-axis, not in Quadrant III. 5 -8. 18. pos. correlation 19. no correlation 20. (– 3, 4) 21. (5, 0) 22. (6, – 6) 23. (– 3, – 2), (1, 3), (2, – 4) 16. 24. a. Answers may vary. Sample: (– 1, 1), (– 2, 2), (10, – 10) b. Answers may vary. Sample: (1, 1), (– 2, 2), (– 10, – 10) 9. II 10. x–axis 1 -9
Graphing Data on the Coordinate Plane ALGEBRA 1 LESSON 1 -9 27. 25. isosceles triangle square 30. Pos. correlation; the greater the number of cars, the higher the pollution levels for a city. 28. 26. rhombus 29. Neg. correlation; the more classes you take, the more work you have, so the less free time you have. rectangle 31. No correlation; baby’s length at birth is not related to its birthday. 1 -9

Graphing Data on the Coordinate Plane ALGEBRA 1 LESSON 1 -9 32. Pos. correlation; the more you exercise, the more calories you burn. 35. a. 34. a. Neg. correlation; rain or snow makes b. travel more difficult or inconvenient, so voters would be less likely to go to the polls. 33. Answers may vary. Samples: Pos. correlation; b. Answers may vary. the number of hours a Sample: In general, person earning an hourly the weather has the wage works and the size same effect on both of the paycheck. Neg. sides, but candidates correlation; the number usually want as many of people working on a votes as possible, so project and the time it they should be concerned. takes to complete the project. No correlation; person’s height and the length of his or her hair. 1 -9 neg. correlation Answers may vary. Sample: No; it is generally not reasonable to conclude that correlation between two trends implies cause.

Graphing Data on the Coordinate Plane ALGEBRA 1 LESSON 1 -9 36. a, b. 36. (continued) d. Answers may vary. Sample: about 200 cal 37. 20 units; 21 square units 38. 7. 5 square units b. pos. correlation c. In general, it appears that the greater the number of grams of fat in a serving of food, the greater the number of calories. 39. Answers may vary. Sample: There is a circle with radius 5 and center (2, 3) that contains the points (– 1, – 1), (– 2, 0), (– 2, 6), (– 1, 7), (5, 7), (6, 6), (6, 0), and (5, – 1). (It also contains the points (– 3, 3), (2, 8), (7, 3), and (2, – 2). ) 1 -9

Graphing Data on the Coordinate Plane ALGEBRA 1 LESSON 1 -9 40. a. the distance a car traveled on the Indiana toll road and the toll charged b. The points have the same x-coordinate; that is, they lie on the same vertical line. c. The points have the same y-coordinate; that is, they lie on the same horizontal line. d. Pos. correlation; in general, as distance increases, the toll increases. 41. C 44. G 45. A 46. H 47. x – 4(2 x + 1) – 3 = x – 8 x – 4 – 3 Dist. Prop. = 1 x – 8 x – 4 – 3 Ident. Prop. of Mult. = 1 x + (– 8 x) + (– 4) + (– 3) def. of subtr. = [1 x + (– 8 x)] + [(– 4) + (– 3)] Assoc. Prop. of Add. = [1 + (– 8)]x + (– 4) + (– 3) Dist. Prop. = – 7 x + (– 4) + (– 3) add. = – 7 x + (– 7) add. = – 7 x – 7 def. of subtr. 42. G 43. D 1 -9

Graphing Data on the Coordinate Plane ALGEBRA 1 LESSON 1 -9 48. 5(8 t) + 4(9 – t) – 37 = 40 t + 36 – 4 t – 37 Dist. Prop. = 40 t + 36 + (– 4 t) + (– 37) def. of subtr. = 40 t + (– 4 t) + 36 + (– 37) Comm. Prop. of Add. = [40 t + (– 4 t)] + [36 + (– 37)] Assoc. Prop. of Add. = [40 + (– 4)]t + [36 + (– 37)] Dist. Prop. = 36 t + (– 1) add. = 36 t – 1 def. of subtr. 49. 8 b + 7 a – 4 b – 9 a = 8 b + 7 a + (– 4 b) + (– 9 a) def. of subtr. = 8 b + (– 4 b) + 7 a + (– 9 a) Comm. Prop. of Add. = [8 b + (– 4)b] + [7 a + (– 9)a] Assoc. Prop. of Add. = [8 + (– 4)]b + [7 + (– 9)]a Dist. Prop. = 4 b + (– 2)a add. = 4 b – 2 a def. of subtr. 1 -9

Graphing Data on the Coordinate Plane ALGEBRA 1 LESSON 1 -9 50. 3 m 2 – (10 m + 3 m 2) = 3 m 2 – 1(10 m + 3 m 2) Mult. Prop. of – 1 = 3 m 2 – 10 m – 3 m 2 Dist. Prop. = 3 m 2 + (– 10 m) + (– 3 m 2) def. of subtr. = 3 m 2 + (– 3 m 2) + (– 10 m) Comm. Prop. of Add. = [3 + (– 3)]m 2 + (– 10 m) Dist. Prop. = 0 m 2 + (– 10 m) Inv. Prop. of Add. = 0 + (– 10 m) Mult. Prop. of Zero = – 10 m Ident. Prop. of Add. 51. 9 – 13 19 – 1 3. 1 – 4. 9 – 11 5 – 0. 7 – 4. 7 – 7 21 – 2. 1 8 1 -9 30 55. true 56. false; 1 = 12 57. true 52. [16. 5 – 29 1 – 9. 5] 53. 1 1 – 2 2 10 1 – 17 2 54.

Graphing Data on the Coordinate Plane ALGEBRA 1 LESSON 1 -9 Use the graph for 1 – 6. Name the coordinates of each point. 1. A 2. D 3. F (– 3, – 3) (– 2, 1) (2, 0) 5. In which quadrant is point E? II 6. Describe the trend. positive correlation 1 -9 4. G (3, 2)

Tools of Algebra ALGEBRA 1 CHAPTER 1 1. n = number, c = cost, c = 2. 3 n 2. p = payment, c = change, c = 10 – p 3. 4 4. 0 5. 5 18. 12 d – 30 11. 1 4 5 19– 20. Answers may vary. 12. 18 13. 14. 11 2 1 19. 10 x + 3( – x) – 3 5 – 1 13 – 10 3 15 – 1 5 9 6. 12 7. 5 8. 6 – 11 2 – 10 1 15. False, since is a 2 rational number but is not an integer. 9. – 20 16. False, since |0| = 0, which is not pos. 10. – 10 17. – 3 + 18 a 1 -A = 10 x + 1 – 3 x Dist. Prop. = 1 + 10 x – 3 x Comm. Prop. of Add. = 1 + (10 – 3)x Dist. Prop. = 1 + 7 x subtr. 20. (33 – 33)(1 – 22) = (33 + (– 33))(1 – 22) def. of subtr. = 0(1 – 22) Inv. Prop. of Add. = 0 Mult. Prop. of Zero

Tools of Algebra ALGEBRA 1 CHAPTER 1 21. – 10(2 – 11) 5 m + 6 5 1 23. (p – )( + p) 8 4 24. – 10 3 8 22. 25. 2. 7 26. a. Sometimes; 5 – 3 = 2, but 3 – 5 = – 2. b. Never; 3 – (– 2) = 5 and 8 – (– 10) = 18. c. Sometimes; – 8 – (– 3) = – 5, but – 3 – (– 8) = 5. d. Never; – 3 – (8) = – 11 and – 7 – (10) = – 17. 27. Answers may vary. Sample: 2 – , 1. 5, 1, – 1 6 3 34. neg. correlation 35. about 41°F 36. If a and b have different signs, 2 1 – , 1, 1. 5 3 6 28. y-axis 29. Quadrant III 30. 28 square units 31. 2 yd lost 32. $177 33. $19. 30 1 -A a | | is positive b and is negative.
67a634751c2256d5d2e50d00356566f6.ppt