USING THE HISTORY OF MATHEMATICS IN TEACHING George

USING THE HISTORY OF MATHEMATICS IN TEACHING George Gheverghese Joseph

WHY INCLUDE HISTORY OF MATHEMATICS IN TEACHING? “The teacher who knows little of the history of mathematics is apt to teach techniques in isolation, unrelated either to the problems and ideas which generated them or to the further developments which grew out of them”. From a UK Ministry of Education report of 1958

WHY INCLUDE HISTORY OF MATHEMATICS IN TEACHING? “Students should learn to study at an early stage the great [historical] works …. instead of making their minds sterile through everlasting exercises …. which are of no use whatsoever …. . where indolence is veiled under the form of useless activity”. (Eugenio Beltrami, 1873)

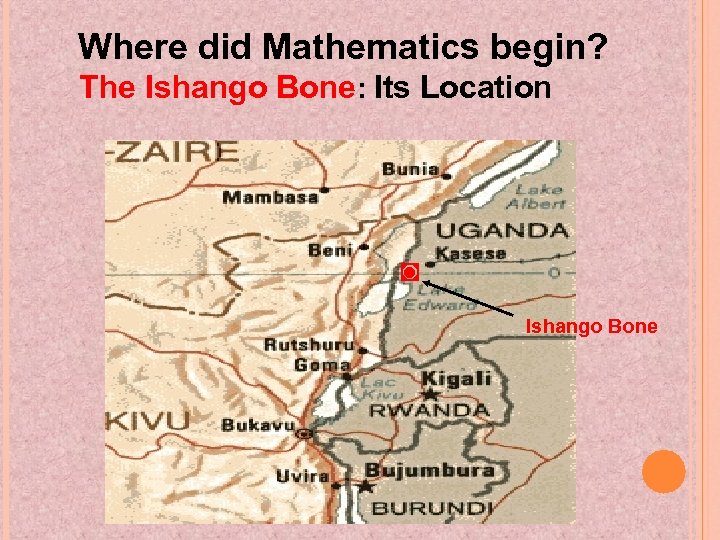Where did Mathematics begin? The Ishango Bone: Its Location ◙ Ishango Bone

The Ishango Bone (dated 25000 – 20000 BC)

WHAT IS THE MATHS [HIS]STORY BEHIND THIS 1835 PAINTING BY TURNER?

THE 1835 PAINTING BY TURNER DEPICTS THE HOUSES OF PARLIAMENT BURNING IN 1834 BACKGROUND Some resistance to the adoption of new arithmetic afforded by the Indo-Arabic numerals. Tally sticks were in use until the 19 th century. The fire was caused by tally sticks kept in the houses. Charles Dickens commented at the time: In 1834. . . there was a considerable accumulation of them [tally sticks]. . The sticks were housed in Westminster…… and so the order went out that they should be privately and confidentially burned. It came to pass that they were burned in a stove in the House of Lords. The stove, over gorged with these preposterous sticks, set fire to the paneling; the paneling set fire to the House of Commons. ”

A MATHEMATICAL DIFFERENCE BETWEEN TWO PAINTINGS MELCHIOR BROEDERLAM (C. 1394) PIETRO PERUGINO FRESCO AT THE SISTINE CHAPEL (1481)

PERSPECTIVE – HOW GEOMETRY INFLUENCED ART Florentine architect Brunelleschi (1377 – 1446 ): First in Europe to carry out a series of experiments leading to a geometrical theory of perspective. Essentially parallel lines on a horizontal plane depicted in the vertical plane meet – at the vanishing point After his discovery artists adopted perspective and since then paintings depicting real life scenes have been more realistic. Perugino’s fresco at the Sistine Chapel (1481) clearly shows perspective while Broederlam’s 1394 painting does not (Brunelleschi had not yet discovered the rules of perspective). Cuboid with 1 vanishing point

FOR EXAMPLE MELCHIOR BROEDERLAM (1394) PIETRO PERUGINO FRESCO AT THE SISTINE CHAPEL (1481)

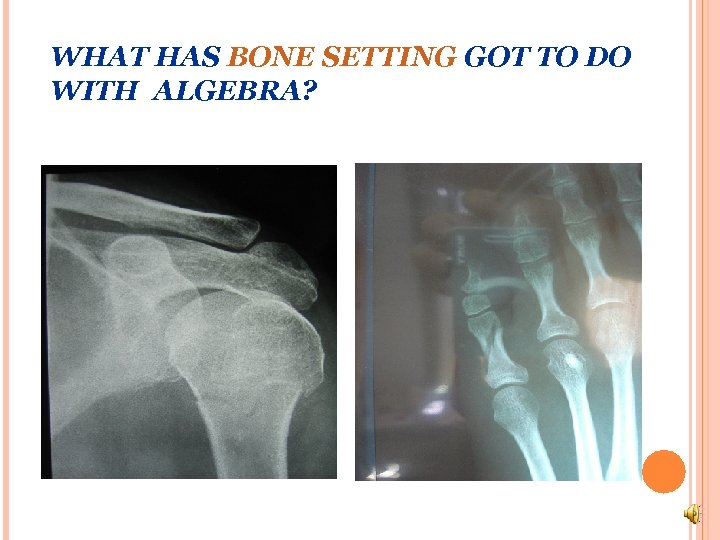WHAT HAS BONE SETTING GOT TO DO WITH ALGEBRA?

WHAT HAS BONE SETTING GOT TO DO WITH ALGEBRA? Al-Khwarizmi wrote the first treatise on algebra: Hisab al-jabr w’al-muqabala in 820 AD. The word algebra is a corruption of al-jabr which means restoration of bones. In Spain, where the Moors from North Africa held sway for a long period, there arose a profession of ‘algebristas’ who dealt in bone setting. álgebra. 1. f. Parte de las matemáticas en la cual las operaciones aritméticas son generalizadas empleando números, letras y signos. 2. f. desus. Arte de restituir a su lugar los huesos dislocados (translation: the art of restoring broken bones to their correct positions)

Some ways to convince students that the mathematics they study has the trace of history: -

TRACE OF HISTORY Writing in English proceeds from the Left to the Right: Just as you are reading this sentence?

THE TRACE OF HISTORY Roman numbers can be read from the Left to the Right: C X V 100 10 5

THE TRACE OF HISTORY But Our Place value number structure proceeds from the Right to the Left: So to interpret a whole number 72 | 611 | 134 | 942 | 342 |835 you naturally/normally proceed [in blocks of 3 places] from the Right to the Left to finally identify place value of the numeral 7.

THE TRACE OF HISTORY Early Indian systems were both Left to the Right and Right to the Left systems. Conjecture: The Arabs following the practice of writing Arabic naturally adopted the Right to the Left and transmitted it Westwards.

SIMILARLY OPERATIONS WITH THE INDO-ARABIC NUMERALS

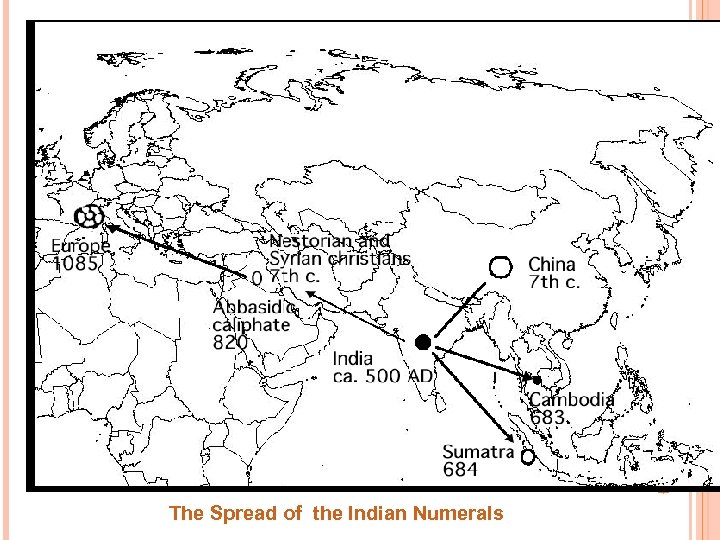The Spread of the Indian Numerals

WHY IS 1= 0. 99999. . . . ? A PROOF FROM HISTORY FOR A SCEPTIC IN A SENIOR CLASS Derived from a 16 th century mathematical manuscript (Yuktibhasa) from Kerala, South India: 1 = 1. 10 = 1. [9 + 1] = 1. [1+ 1] 9 10 9 Use Identity identity. 1 1. [1+ 1]: 9 10 9 Hence 1 = 1. [1+ 1. [1 + 1 ] = 1 + 1 [1 + 1] 9 10 102 102 9 Keep going. . . . and replace last 1 by the 1 = 1 + 1 +. . . . 9 10 102 103 104 9

WHY IS 1= 0. 99999. . . . ? A PROOF FOR THE SCEPTIC (CONTINUED) 1 = 1 + 1 +. . . . 9 10 102 103 104 Can generalise by replacing 1 by any non-zero numeral a: a = a + a +. . . . 9 10 102 103 104 Now a = 9 implies 9 = 9 + 9 +. . . . 9 10 102 103 104 1 = 0. 999999. . . . Q. E. D

WHY IS 1= 0. 99999. . . . ? THE PROOF GENERALISED FOR GEOMETRIC SERIES Show: 1/(1 -c) = 1 + [1/(1 - c)] c Substitution for (1/(1 - c)) gives 1/(1 -c) = 1 + (1 + [1/(1 - c)] c) c = 1 + c + (1/(1 - c))c 2 Repeated substitution gives 1/(1 – c) = 1 + c 2 + ……………. + cn-1 + cn/(1 – c) Rearranging gives: (1 – cn)/(1 – c) = 1 + c 2 + ……………. + cn-1

LOOKING FOR ‘CALCULATOR MAGIC’ IN THE HISTORY OF MATHS Hero’s (1 st century AD, Alexandria) algorithm for the square root of a number P. Step 1: Guess an approximate square root a 1 for P. Step 2. Second guess is a 2 = ½ (a 1 + P/ a 1) Third guess is a 3 = ½ (a 2 + P/a 2) Fourth guess is a 4 = ½ (a 3 + P/ a 3) In general: (n + 1)st guess is an+1 = ½ (an + P/ an)

‘CALCULATOR MAGIC’ FROM THE HISTORY OF MATHS: HERO’S ITERATION Step 1: Guess an approximate square root a 1 for P. Step 2. Second guess is a 2 = ½ (a 1 + P/ a 1) Third guess is a 3 = ½ (a 2 + P/a 2) Fourth guess is a 4 = ½ (a 3 + P/ a 3) In general: (n + 1)st guess is an+1 = ½ (an + P/ an) a 1 a 2 a 3 a 4 Sq. Root P = 30 5. 5 5. 47727. . 5. 4772255. P = 27 5. 5 5. 20454545. . . 5. 19615919. . 5. 196152423. . . P = 37 5. 5 6. 113636364. . . 6. 082840487. . 6. 082762531. . 6. 08276253. . . 5. 477225575. . .

‘CALCULATOR MAGIC’ FROM THE HISTORY OF MATHS: HERO’S ITERATION (CONTINUED) Hero’s iteration is an+1 = ½ (an + P/ an) Suppose an → L as n → ∞ Then iteration an+1 = ½ (an + P/ an) → L = ½ (L + P/ L) as n → ∞ Solving L = ½ (L + P/ L) gives L 2 = P. That is the limit L = √P

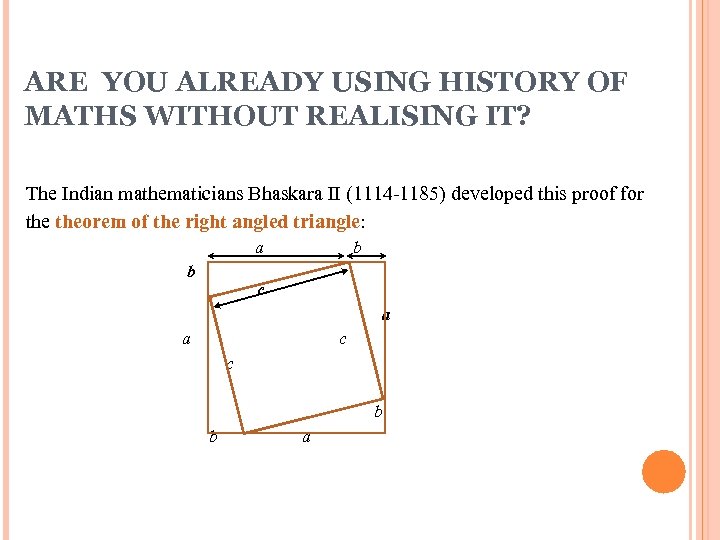ARE YOU ALREADY USING HISTORY OF MATHS WITHOUT REALISING IT? The Indian mathematicians Bhaskara II (1114 -1185) developed this proof for theorem of the right angled triangle: a b b c a a c c b b a

ARE YOU ALREADY USING HISTORY OF MATHS WITHOUT REALISING IT? Area of large square = (a + b)2 Which is made up of inner square of area c 2 and 4 triangles each of area ½ ab So (a + b)2 = c 2 + 4 ½ ab Or a 2 + b 2 + 2 ab = c 2 + 2 ab Thus a 2 + b 2 = c 2

HISTORY OF MATHS – ANOTHER PROOF OF ‘PYTHAGORAS’ THEOREM’ Bhaskara II developed another proof for theorem of the right angled triangle using this diagram: How does the figure help show BC 2 = AC 2 + AB 2? A Bhaskara’s Explanation Behold! B C

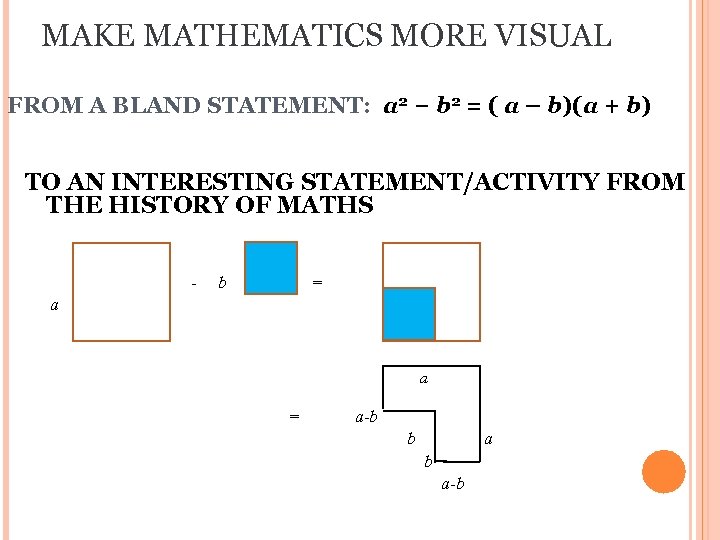MAKE MATHEMATICS MORE VISUAL FROM A BLAND STATEMENT: a 2 − b 2 = ( a – b)(a + b) TO AN INTERESTING STATEMENT/ACTIVITY FROM THE HISTORY OF MATHS - b = a a = a-b b a-b

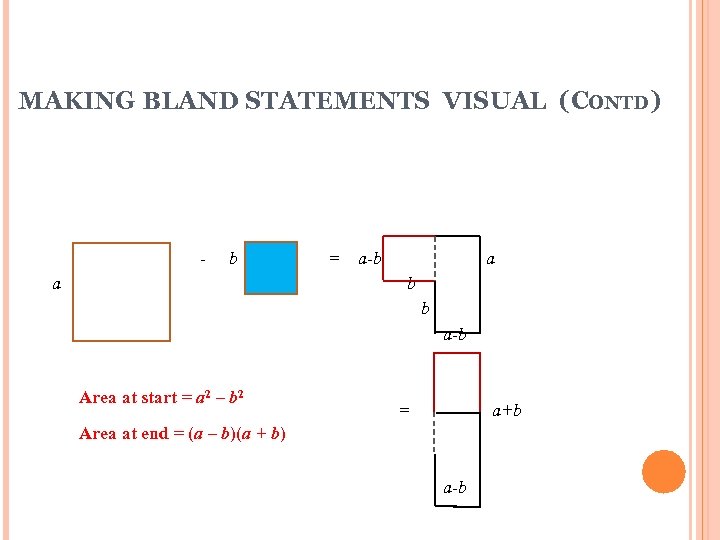MAKING BLAND STATEMENTS VISUAL (CONTD) - b a = a-b a b b a-b Area at start = a 2 – b 2 = a+b Area at end = (a – b)(a + b) a-b

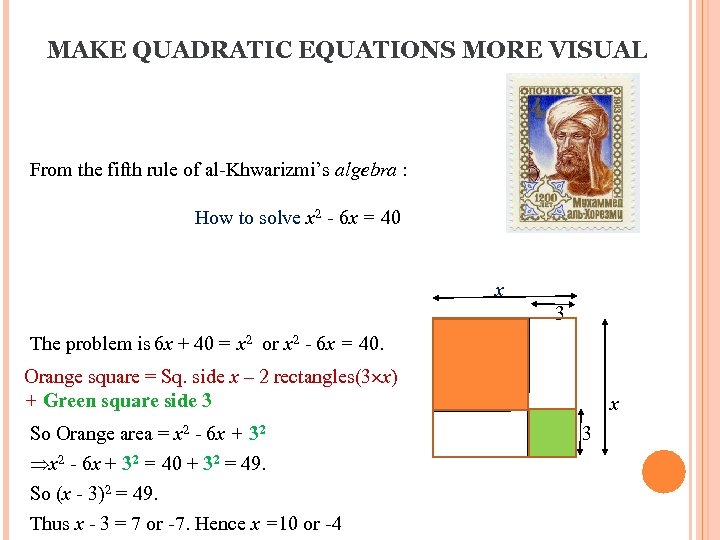MAKE QUADRATIC EQUATIONS MORE VISUAL From the fifth rule of al-Khwarizmi’s algebra : How to solve x 2 - 6 x = 40 x 3 The problem is 6 x + 40 = x 2 or x 2 - 6 x = 40. Orange square = Sq. side x – 2 rectangles(3 x) + Green square side 3 So Orange area = x 2 - 6 x + 32 = 40 + 32 = 49. So (x - 3)2 = 49. Thus x - 3 = 7 or -7. Hence x =10 or -4 x 3

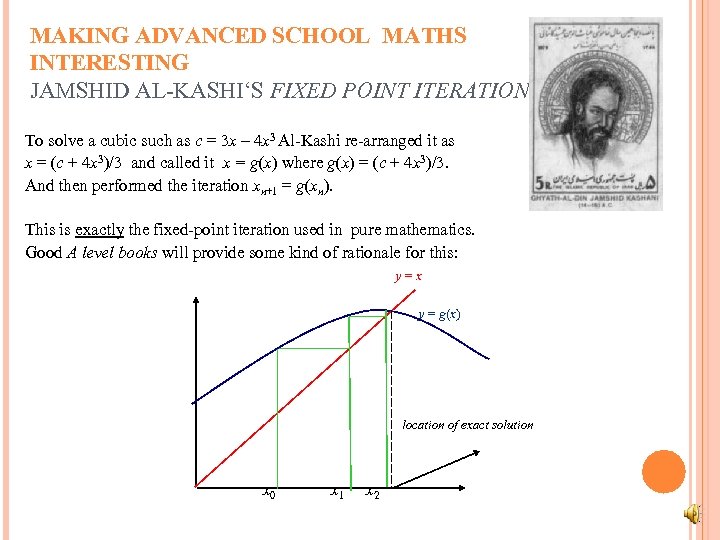MAKING ADVANCED SCHOOL MATHS INTERESTING JAMSHID AL-KASHI‘S FIXED POINT ITERATION To solve a cubic such as c = 3 x – 4 x 3 Al-Kashi re-arranged it as x = (c + 4 x 3)/3 and called it x = g(x) where g(x) = (c + 4 x 3)/3. And then performed the iteration xn+1 = g(xn). This is exactly the fixed-point iteration used in pure mathematics. Good A level books will provide some kind of rationale for this: y=x y = g(x) location of exact solution x 0 x 1 x 2

WHY INCLUDE HISTORY OF MATHEMATICS IN TEACHING? It provides cross-curricular links Art, Spanish It presents mathematics as a global endeavour rather than a monopoly of any single culture. Spread of Indian Numerals It locates mathematics in a cultural context Ishango Bone . . all this should increase interest in learning mathematics in our multi-ethnic world

BRAINSTORMING: REASONS FOR USING HISTORY IN MATHEMATICS EDUCATION 1. Increase motivation for learning 2. Humanizes mathematics 3. Helps to order the presentation of topics in the curriculum 4. Showing how concepts have developed and helps understanding 5. Changes students' perceptions of mathematics

REASONS FOR USING HISTORY IN MATHEMATICS EDUCATION (CONTINUED) 6. Comparing ancient and modern helps in understanding the value of the latter 7. Helps develop a multicultural approach 8. Provides opportunities for investigation 9. Past difficulties a good indication of present pitfalls 10. Students derive comfort from realizing that they are not the only ones with problems.

REASONS FOR USING HISTORY IN MATHEMATICS EDUCATION (CONTINUED) 11. Encourages quicker learners to look further 12. Helps to explain the role of mathematics in society 13. Makes mathematics less frightening 14. Exploring history helps to sustain a teacher’s own interest and excitement 15. Provides opportunities for cross-curricular work with other teachers or subjects