Using Random Forests Language Models in IBM RT-04

Using Random Forests Language Models in IBM RT-04 CTS Peng Xu 1 and Lidia Mangu 2 1. 2. 1. CLSP, the Johns Hopkins University 2. IBM T. J. Waston Research Center March 24, 2005 IBM T. J. Waston CLSP, The Johns Hopkins University 1

n-gram Smoothing: take out some probability mass from seen n-grams and distribute among unseen n-grams n n Over 10 different smoothing techniques were proposed in the literature. Interpolated Kneser-Ney: consistently the best performance [Chen & Goodman, 1998] IBM T. J. Waston CLSP, The Johns Hopkins University

More Data… There’s no data like more data n n n [Berger & Miller, 1998] Just-in-time language model. [Zhu & Rosenfeld, 2001] Estimate n-gram counts from web. [Banko & Brill, 2001] Efforts should be directed toward data collection, instead of learning algorithms. [Keller et. al. , 2002] n-gram counts from the web correlates reasonably well with BNC data. [Bulyko et. al. , 2003] Web text sources are used for language modeling. [RT-04] U. of Washington web data for language modeling. IBM T. J. Waston CLSP, The Johns Hopkins University

More Data more data solution to data sparseness n n The web has “everything”: web data is noisy. The web does NOT have everything: language models using web data still have data sparseness problem. w [Zhu & Rosenfeld, 2001] In 24 random web news sentences, 46 out of 453 trigrams were not covered by Altavista. n In domain training data is not always easy to get. Do better smoothing techniques matter when training data is of millions of words? IBM T. J. Waston CLSP, The Johns Hopkins University

Outline Motivation Random Forests for Language Modeling n n Decision Tree Language Models Random Forests Language Models Experiments n n Perplexity Speech Recognition: IBM RT-04 CTS Limitations Conclusions IBM T. J. Waston CLSP, The Johns Hopkins University

Dealing With Sparseness in n-gram Clustering: combine words into groups of words n All components need to use smoothing. [Goodman, 2001] Decision trees: cluster histories into equivalence classes n Appealing idea, but negative results were reported. [Potamianos & Jelinek, 1997] Maximum entropy: use n-grams as features in an exponential model n There is almost no difference in performance from interpolated Kneser-Ney models. [Chen & Rosenfeld, 1999] Neural networks: represent words with real vectors n The models rely on interpolation with Kneser-Ney models in order to get superior performance. [Bengio, 1999] IBM T. J. Waston CLSP, The Johns Hopkins University

Our Motivation Better smoothing technique is desirable. n n Better use of available data is often important! Improvements in smoothing should help other means of dealing with data sparseness problem. IBM T. J. Waston CLSP, The Johns Hopkins University

Our Approach Extend the appealing idea of history clustering from decision trees. n Overcome problems in decision tree construction …by using Random Forests! IBM T. J. Waston CLSP, The Johns Hopkins University

Decision Trees Language Models Decision trees: equivalence classification of histories n n Each leaf is specified by the answers to a series of questions which lead to the leaf from the root. Each leaf corresponds to a subset of the histories. Thus histories are partitioned (i. e. , classified). IBM T. J. Waston CLSP, The Johns Hopkins University

Construction of Decision Trees Data Driven: decision trees are constructed on the basis of training data The construction requires: 1. 2. 3. The set of possible questions A criterion evaluating the desirability of questions A construction stopping rule or post-pruning rule IBM T. J. Waston CLSP, The Johns Hopkins University

Decision Tree Language Models: An Example: trigrams (w-2, w-1, w 0) Questions about positions: “Is w-i 2 S? ” and “Is w-i 2 Sc? ” There are two positions for trigram. Each pair, S and Sc, defines a possible split of a node, and therefore, training data. § S and Sc are complements with respect to training data A node gets less data than its ancestors. (S, Sc) are obtained by an exchange algorithm. IBM T. J. Waston CLSP, The Johns Hopkins University

Decision Tree Language Models: An Example Training data: aba, aca, bcb, bbb, ada {ab, ac, bb, ad} a: 3 b: 2 Is the first word in {a}? New event ‘adb’ in test {ab, ac, ad} a: 3 b: 0 IBM T. J. Waston New event ‘cba’ in test: Stuck! Is the first word in {b}? New event ‘bdb’ in test {bc, bb} a: 0 b: 2 CLSP, The Johns Hopkins University

Construction of Decision Trees: Our Approach Grow a decision tree until maximum depth using training data n n n Questions are automatically obtained as a tree is constructed Use training data likelihood to evaluate questions Perform no smoothing during growing Prune fully grown decision tree to maximize heldout data likelihood n Incorporate KN smoothing during pruning IBM T. J. Waston CLSP, The Johns Hopkins University

Smoothing Decision Trees Using similar ideas as interpolated Kneser-Ney smoothing: Note: n n All histories in one node are not smoothed in the same way. Only leaves are used as equivalence classes. IBM T. J. Waston CLSP, The Johns Hopkins University

Problems with Decision Trees Training data fragmentation: n As tree is developed, the questions are selected on the basis of less and less data. Optimality: § The exchange algorithm is a greedy algorithm. § So is the tree growing algorithm. Overtraining and undertraining: n n Deep trees: fit the training data well, will not generalize well to new test data. Shallow trees: not sufficiently refined. IBM T. J. Waston CLSP, The Johns Hopkins University

Amelioration: Random Forests Breiman applied the idea of random forests to relatively small problems. [Breiman 2001] § Using different random samples of data and randomly chosen subsets of questions, construct K decision trees. § Apply test datum x to all the different decision trees. • Produce classes y 1, y 2, …, y. K. § Accept plurality decision: IBM T. J. Waston CLSP, The Johns Hopkins University

Example of a Random Forest T 1 T 2 a T 3 a a a An example x will be classified as a according to this random forest. IBM T. J. Waston CLSP, The Johns Hopkins University

Random Forests for Language Modeling Two kinds of randomness: n Selection of positions to ask about w Alternatives: position 1 or 2 or the better of the two. n Random initialization of the exchange algorithm 100 decision trees: ith tree estimates PDT(i)(w 0|w-2, w-1) The final estimate is the average of all trees IBM T. J. Waston CLSP, The Johns Hopkins University

Experiments Perplexity (PPL): n n UPenn Treebank part of WSJ: about 1 million words for training and heldout (90%/10%), 82 thousand words for test Normalized text IBM T. J. Waston CLSP, The Johns Hopkins University

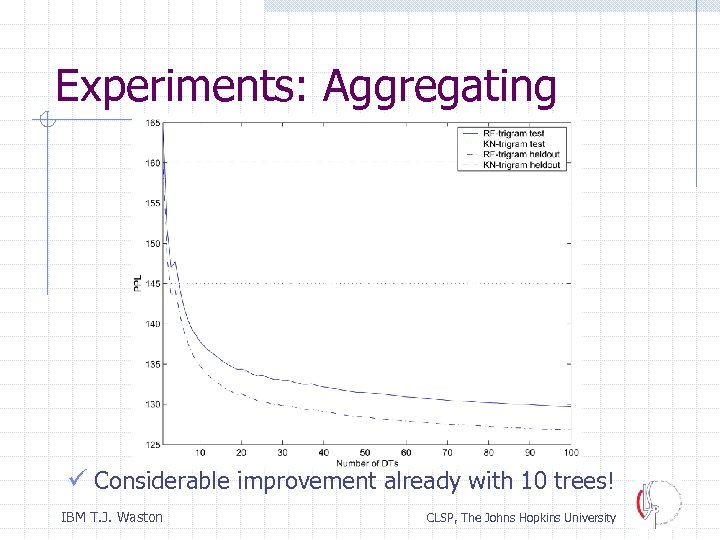
Experiments: Aggregating ü Considerable improvement already with 10 trees! IBM T. J. Waston CLSP, The Johns Hopkins University

Embedded Random Forests Smoothing a decision tree: Better smoothing: embedding! IBM T. J. Waston CLSP, The Johns Hopkins University

Speech Recognition Experiments Word Error Rate by Lattice Rescoring n IBM 2004 Conversational Telephony System for Rich Transcription w Fisher data: 22 million words w WEB data: 525 million words, using frequent Fisher ngrams as queries w Other data: Switchboard, Broadcast News, etc. n n Lattice language model: 4 -gram with interpolated Kneser-Ney smoothing, pruned to have 3. 2 million unique n-grams Test set: DEV 04 IBM T. J. Waston CLSP, The Johns Hopkins University

Speech Recognition Experiments Baseline: KN 4 -gram 110 random DTs Sampling data without replacement Fisher+WEB: linear interpolation Embedding in Fisher RF, no embedding in WEB RF Fisher 4 -gram KN 14. 1% 13. 7% RF 13. 5% 13. 1% p-value IBM T. J. Waston Fisher+WEB 4 -gram <0. 001 CLSP, The Johns Hopkins University

Practical Limitations of the RF Approach Memory: n n Decision tree construction uses much more memory. It is not easy to realize performance gain when training data is really large. Because we have over 100 trees, the final model becomes too large to fit into memory. Computing probabilities in parallel incurs extra cost in online computation. Effective language model compression or pruning remains an open question. IBM T. J. Waston CLSP, The Johns Hopkins University

Conclusions: Random Forests New RF language modeling approach More general LM: RF DT n-gram Randomized history clustering Good generalization: better n-gram coverage, less biased to training data Significant improvements in IBM RT-04 CTS on DEV 04 IBM T. J. Waston CLSP, The Johns Hopkins University

Thank you! IBM T. J. Waston CLSP, The Johns Hopkins University