Using Markov Chain Monte Carlo To Play Trivia

Using Markov Chain Monte Carlo To Play Trivia Daniel Deutch ICDE ‘ 11 [Deutch, Greenshpan, Kostenko , Milo] PODS ‘ 10 [Deutch, Koch, Milo] Web. DAM meeting March 2011

Our goal • Answering trivia questions automatically • Based on knowledge collected from a crowd of users (human Trivia Players) • Some of this knowledge is erroneous – But we don’t know which • Some of the users are more credible than others – But we don’t know in advance the credibility of all users 2

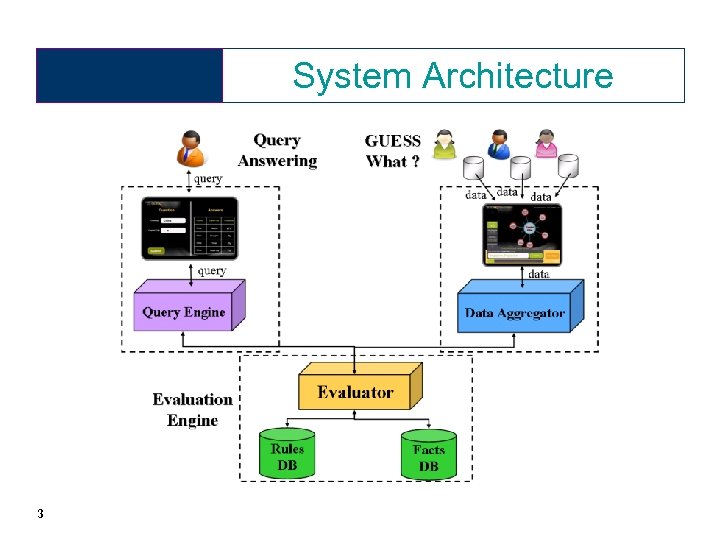System Architecture 3

Trivia Game 4

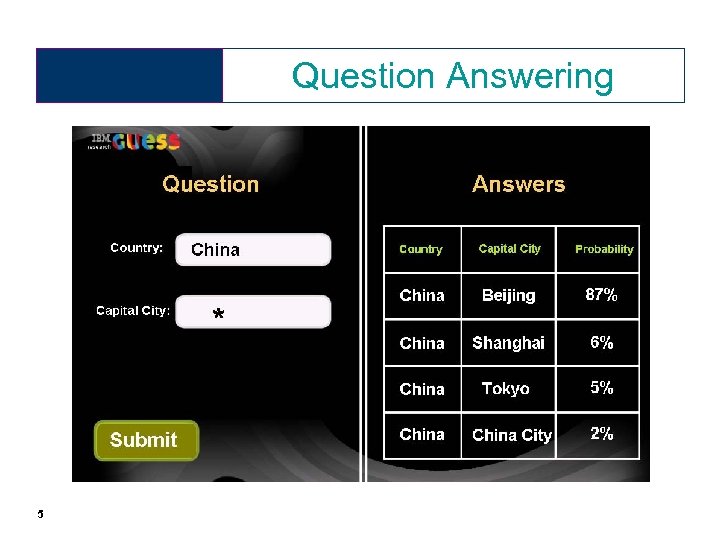Question Answering 5

Motivating Example Say that we collect information on Basketball players and their teams Player Team Support Gasol Memphis 300 Gasol Lakers 100 Duncan San Antonio 50 Duncan New Jersey 50 [Support is the number of people who claimed the fact to be true] Now we want to answer questions • • 6 Simple ones: “Where does Gasol play? ” Or more complex, involving additional information: “Which team has the greatest number of players taller than 7 ft? ”

How would we answer? • By majority vote? • But some people know NBA basketball better than others. . • So maybe a “biased vote”? • But how to bias? • A “chicken or the egg” problem: To know what is true we need to know who to believe. But to know who to believe we need to know who is usually right (and in particular, what is true. . ) 7

So what can we do? • Start with some estimation on the trust in users • Gain confidence in facts based on the opinion of users that supported them – Give more weight to users that we trust • Then update the trust level in users, based on how many of the facts which they submitted, we believe • Iterate until convergence Trusted players give us confidence in facts, and players that supported these facts gain our trust… 8

(One possible) Probabilistic Algorithm Start with some prior belief in every user do { Probabilistically choose a correct team for every player based on popular support (biased by the belief in users) Evaluate the query, add a point to every obtained query result Increase your belief in every user that supported the chosen assertion } until (convergence of the ratio of results) 9

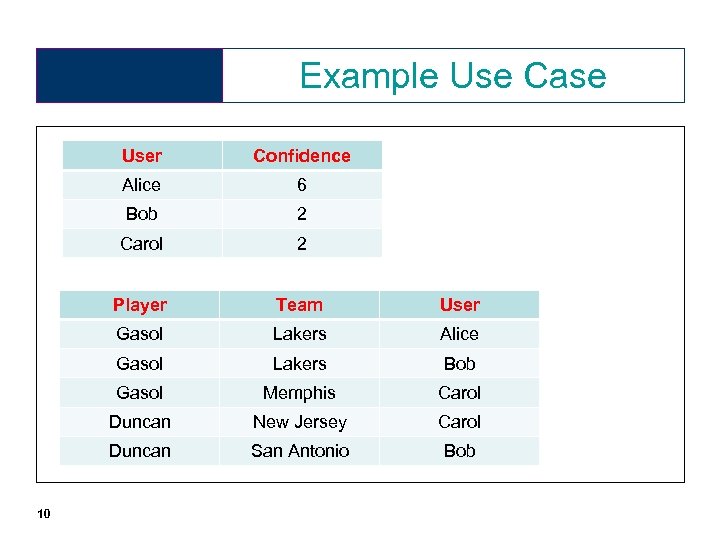Example Use Case User Alice 6 Bob 2 Carol 2 Player Team User Gasol Lakers Alice Gasol Lakers Bob Gasol Memphis Carol Duncan New Jersey Carol Duncan 10 Confidence San Antonio Bob

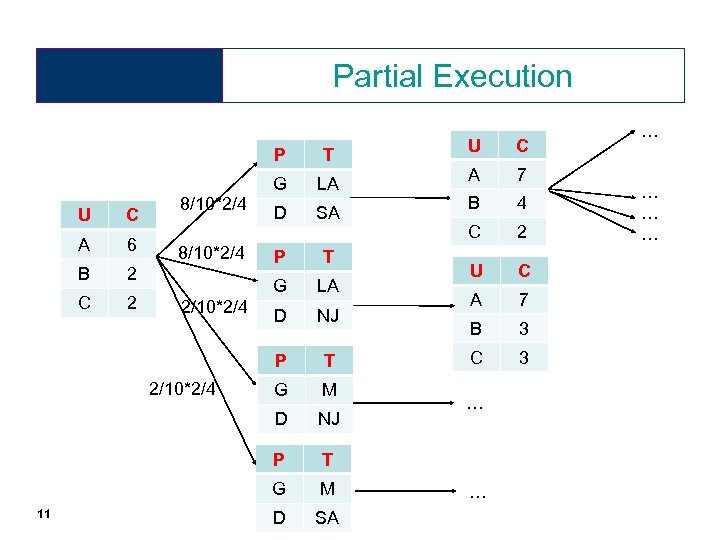Partial Execution P B C 2 2/10*2/4 11 P T G 2 8/10*2/4 SA LA D NJ T G M NJ M D SA C A 7 B 4 C 2 U C A 7 B 3 C 3 T G 6 D P A LA D C G P U 8/10*2/4 T U … … …

What’s going on? • We believe Alice, But we don’t know whether to believe Bob or Carol Hence don’t know if Duncan plays for NJ or SA [Note that (weighted) majority vote won’t help us in deciding this] • We have some reason to believe Bob more: We think he was correct saying that Gasol plays for LA [We think this because we believe Alice] [Therefore Bob may have better Basketball knowledge] • In general things are more complex(more users, facts. . ) 12

What’s going on? (cont. ) With high probability, Bob will eventually gain a significant advantage (over Carol) in his confidence level – At the first step there’s • 40% chance of him getting a two points gain over Carol, • 40% chance of them having the same confidence level, • 20% chance for Carol to win a one point gain over Bob – If Bob (eventually) wins an advantage, his chances of winning an extra advantage become even higher in the following steps – With good chance, we will eventually get “almost certain” that Alice and Bob are both more credible than Carol • And will conclude that Duncan Plays for San Antonio 13

Sampling • We can repeat the algorithm N times, each time restarting the confidence levels to their original ones • In our example, almost 80% of the executions will result in believing that Duncan plays for SA • Our automated Trivia query engine can answer “SA” to “Where does Duncan play? ”, with good confidence • This kind of algorithm is called Markov Chain Monte Carlo 14

Markov Chain • Markov Chain: – Finite State Machine with probabilities on its transitions – Markovian Property: the next state is independent of the past states (given the current state) • In our case the states correspond to database instances • The probabilities on the transitions are determined by the algorithm 15

Monte Carlo • A Monte Carlo algorithm – A general term for an algorithm that relies on sampling [We sample here over multiple traversals on the Markov Chain] • Monte Carlo algorithms are by nature approximation algorithms • But they approximate pretty well in practice 16

General Policies • The algorithm we have presented is useful by itself • We could implement it in Java and use it – But this may be complex for large datasets… • Also, there are many other algorithms in the literature • Conclusion: – We want to have easy control on the employed policy – We really don’t want to rewrite Java code for each tiny change! – We want (seamless) optimization, update propagation. , , , 17

General Policies (cont. ) • Database approach: define a declarative language for specifying policies • We defined a new language [PODS ‘ 10] which combines datalog (for recursion) with a way of making probabilistic choices • Using this language we can define MCMC algorithms! • Declarative specifications are robust, generic, and allow optimizations. 18

General Policies (cont. ) • Add to datalog a REPAIR-KEY (RK) [Koch ‘ 09] construct • REPAIR-KEY “repairs” key violations (=contradictions) in the database, choosing one possible option, probabilistically, according to the sum of support in this option, relative to the other options 19

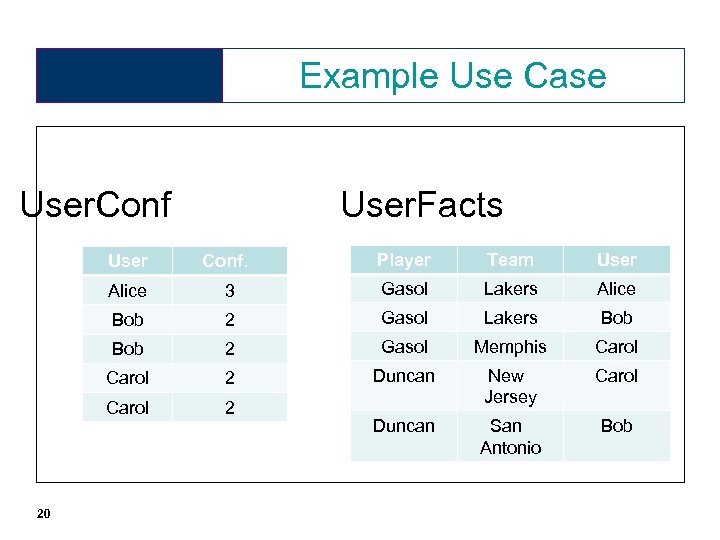Example Use Case User. Conf User. Facts User Player Team User Alice 3 Gasol Lakers Alice Bob 2 Gasol Lakers Bob 2 Gasol Memphis Carol 2 Duncan 2 New Jersey Carol 20 Conf. Duncan San Antonio Bob

Implementation in probabilistic datalog DROP Believed. Facts; INSERT INTO Believed. Facts REPAIR-KEY[Player @ Confidence] ON User. Facts INNER JOIN Users. Conf; 21

Implementation in probabilistic datalog UPDATE Users. Conf, Q 1 SET Users. Conf. confidence = Q 1. Correct. Facts + Users. Conf. confidence WHERE Users. Conf. user = Q 1. user; Q 1 = SELECT user, COUNT(DISTINCT player) As Correct. Facts FROM Q 2 GROUP BY user; Q 2 = SELECT user, team, player FROM User. Facts UF WHERE EXIST (SELECT * FROM Believed. Facts BF WHERE BF. player = UF. player AND BC. team = UF. team) 22

Semantics • The prob. of a query result is the probability that it appears in the evaluation on the database, at an arbitrary point of the walk • More formally: – The probability of observing a sequence seq = [s 1, …, sn] is the multiplication of transition probabilities – Let |seq| denote the length of seq – Given a database state s, Pr(s)= | – The prob. of a tuple t is the sum of Pr(s) over all s for which t appears in Q(s) |

Some Complexity Results Problem: Given a “probabilistic datalog” program and an SQL query on the database (“where does Duncan play”), compute the probabilities of the different answers to appear at a random time of the walk. • Theorem: Exact computation is NP-hard • Theorem: If the MC is ergodic, then computable in EXPTIME in number of states • • Compute the stochastic matrix of transitions Compute its fixpoint For ergodic Markov Chain corresponds to correct probabilities Sum up probabilities of states where the query event holds • Theorem: In general, 2 -EXPTIME • Apply the above to each connected component of the Markov Chain • Factor by probability of being in each component 24

Approximation Algorithms Approximations: – Absolute approximation: approximates correct probability ±ε – Relative approximation: approximates correct probability up to a factor in-between (1 - ε), (1+ ε). [Relative is harder to achieve] • Theorem: No PTIME (randomized) approximation exists unless P=NP • • • 25 Reduction from 3 -SAT Construct a MC that probabilistically chooses assignments Query event asks whether the given assignment is satisfying Such assignment will be found with prob. > 0 iff exists Consequently deciding if the probability is 0 or not is hard

Approximation Algorithms (cont. ) • Theorem: For ergodic underlying MC, randomized absolute approximation possible in PTIME w. r. t. DB size and MC mixing time • The PTIME algorithm is a sampling algorithm [In the spirit of the algorithm demonstrated earlier. ] 26

Other important issues • How (and when) can we evaluate things fast enough? • How to store the vast amount of data? • Distributed Databases? Map-reduce? • How to motivate users to contribute useful facts? • • • First need to find what data is needed/missing… Give user points, based on answers novelty & correctness ? But we do not know which answers are correct ! Well, we can use our estimation algorithm… Other possible techniques? • The data keeps changing. How to handle updates? 27