Using Efficiency Analysis to Measure Individual Well-Being with

Using Efficiency Analysis to Measure Individual Well-Being with an illustration for Catalonia Xavi Ramos UAB & IZA 1

Outline § Explain how distance functions can be adapted to measure multidimensional wellbeing, and thus poverty (Lovell et al. 1994) § Apply the methodology to data for Catalonia, 2000. § Draw some policy implications and conclude. 2

Distance Functions and Well-Being § Distance functions measure the distance between a given (output or input) vector and a benchmark vector as the (inverse) of the factor by which the vector has to be scaled (up or down) to be on the benchmark vector. § To measure well-being the benchmark is taken to be the individual with highest/lowest well-being. § Then, the distance function measures by how much individual’s attributes have to be expanded or contracted to have the same level of well-being as the benchmark. This is our measure of well-being. 3

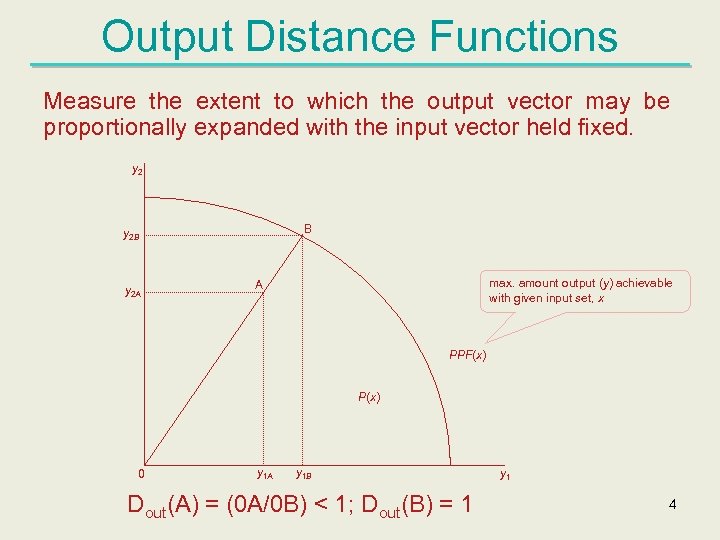
Output Distance Functions Measure the extent to which the output vector may be proportionally expanded with the input vector held fixed. y 2 B y 2 A max. amount output (y) achievable with given input set, x A PPF(x) P(x) 0 y 1 A y 1 B Dout(A) = (0 A/0 B) < 1; Dout(B) = 1 y 1 4

Output Distance Functions Dout(x, y) = min { : (y/ ) P(x)} Properties § § Non-decreasing, linearly homogeneous in y Decreasing in x Dout(x, y) ≤ 1 if y P(x) Dout(x, y) = 1 if y PPF(x) 5

Input Distance Functions Measure the extent to which the input vector may be proportionally contracted given an output vector. x 2 A x 2 A L(y) x 2 B min. amount inputs (x) required to produce given output set, y B IQ(y) 0 x 1 B x 1 A Din(A) = (0 A/0 B) > 1; Din(B) = 1 x 1 6

Input Distance Functions Din(x, y) = max { : (x/ ) L(y)} Properties § § Non-decreasing, linearly homogeneous in x Decreasing in y Dout(x, y) ≥ 1 if y L(y) Dout(x, y) = 1 if y IQ(y) 7

Two stage method Assume well-being stems from achievement in many dimensions of life, which in turn may be captured by a set of indicators Indicators Dimensions Input DF Output DF Dimensions Well-Being 8

Level of Achievement in a Dimension • Empirical Problem: Din(∙) depends on y § Suppose all individuals have the same minimum level of achievement, i. e. one unit. § Reference set becomes IQ(e), bounds input vector from below. § Individuals with input vector on IQ(e) share the lowest level of achievement (=1) § The radially farther away from IQ(e) the higher the level of achievement (> 1) 9

Level of Achievement in a Dimension Estimation procedure: § Normalize using one of the inputs, x. N, § use a trans-log for the resource frontier, and § estimate by COLS: Din(xi, e) = exp{max(ε)- εi} ≥ 1, § which guarantees that all input vectors lie on or above the resource frontier IQ(e) § Warning: if Din(∙) is not homothetic in inputs, Warning results will depend on normalising variable, i. e. x. N. 10

Overall Level of Well-Being Empirical Problem: WB(∙) depends on x § Suppose all individuals have the same minimum level of inputs, i. e. one unit. § Reference set becomes PPF(e), bounds achievement vector from above. § Individuals with achievement vector on PPF(e) share the highest level of well-being (=1) § The radially farther away from PPF(e) the lower the level of achievement (< 1) 11

Overall Level of Well-Being Estimation procedure: As before. Now, § OLS: ln(1/ y. M) = TL(e, y/y. M, β)+ ε § Then, Dout(e, yi) = exp{min(ε)- εi} ≤ 1 § Which guarantees that all dimension vectors lie on or below the achievement frontier PPF(e) § Warning: if Dout(∙) is not homothetic in outputs, results will Warning depend on normalising variable, i. e. y. M. 12

The Data: Pa. D 2000 6 dimensions of Well-being § Health related § Provide Good Education § Work-Life Balance § Housing Conditions § Social Life and Network § Economic Status 13

Correlations § Not doing well in any one dimensions does not imply doing bad in another one [r(dmi, dmj) = low] § More economic resources do not necessarily lead to higher achievement levels in a dimensions [r(dm, y) = low & expected sign] § Any Well-being analysis should take its many dimensions into account –not only income [r(wb, y) = low] § Very low levels of inequality !! [G(wb) = 0. 06; 0. 02 ≤ G(dmi) ≤ 0. 15] 14

Multivariate analysis: Main findings POSITIVE effect § Age up to 41 § Education § Retired § Living near relatives § National Identity: Catalan NEGATIVE effect § Age from 41 § Female § Renting flat § Life shaking event NO effect § Marital status § Labour mkt relation § # employed in HH 15

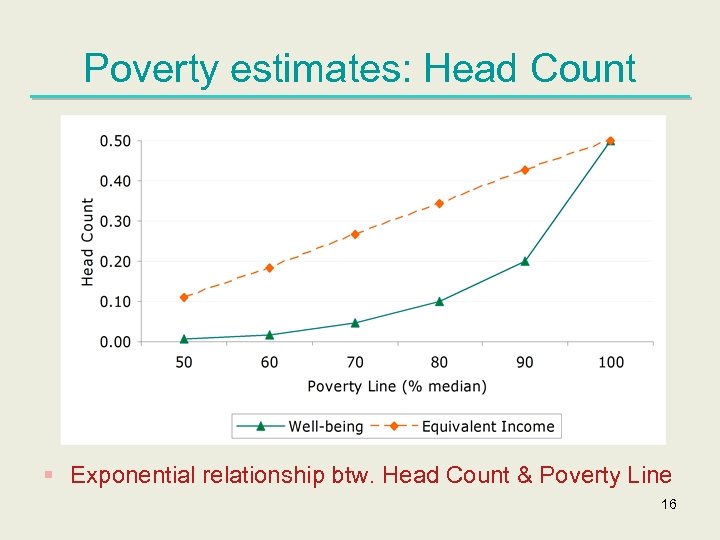
Poverty estimates: Head Count § Exponential relationship btw. Head Count & Poverty Line 16

Well-Being and Income Poverty WB-poor if belongs to the bottom 18. 4% of the WB distribution § Only 5% are Well-Being and Income poor § Two thirds of income poor manage to escape wellbeing poverty § Logit estimates on Well-Being poverty in line with OLS results. But two differences: ü Gender does not condition poverty risk ü Divorced face higher well-being poverty 17

Policy Implications and Conclusions § Our analysis vindicates the necessity to take due account of as many of the many dimensions of well-being as possible. § Well-Being cannot be proxied by happiness or life satisfaction questions § Multivariate analysis seems to indicate that our multidimensional well-being index makes sense. . . … but suffers from one major drawback … 18

Policy Implications and Conclusions § Derived indices display exceedingly equal distributions and very low levels of poverty … probably due to (i) qualitative data (ii) two aggregating stages employed to estimate the overall index of Well-Being. § This should be further investigated if distance function based multidimensional indices are to become widely employed. 19

Using Efficiency Analysis to Measure Individual Well-Being with an illustration for Catalonia Xavi Ramos UAB & IZA 20

Health Related § § Health hinders certain activities Physical disability Psychological disability Self-assessed health status 21

Provide Good Education § Satisfaction with children’s education § Good neighbourhood to bring up children? § School discarded because of its cost? 22

Work-Life Balance § Had to quit job to care for relatives § Satisfaction with amount of leisure time § Satisfaction with amount of time spent with children 23

Housing Conditions § Crowding index (m 2/equivalence scale) § Housing deficiencies which cannot afford repairing § Live in desired dwelling § Reside in desired neighbourhood § Can afford living in a comfortable house? 24

Social Life and Network § Satisfaction with social life § Is there someone who can help if personal problems? § Is there someone who can help if financial problems? § Anyone to help if in need to care for relatives or sick? 25

Economic Status § § Possibility of making ends meet Financial difficulties Amount saved last year Deprivation index 26

Level of Achievement in a Dimension Estimation procedure: § By homogeneity: Din(x/x. N, e) = Din(x, e)/x. N § Since Din(x, e) ≥ 1, then (1/ x. N) ≤ Din(x/x. N, e) § Then (1/ x. N) = Din(x/x. N, e)∙exp(ε), ε ≤ 0 § Assume ln[Din(x/x. N, e)] has a TL(x/x. N, e, β). § OLS: ln(1/ x. N) = TL(x/x. N, e, β)+ ε § Finally, Din(xi, e) = exp{max(ε)- εi} ≥ 1 § Which guarantees that all input vectors lie on or above the resource frontier IQ(e) § Warning: if Din(∙) is not homothetic in inputs, results will depend on Warning normalising variable, i. e. x. N. 27