Using Artificial Markets to Teach Computer Science Through

Using Artificial Markets to Teach Computer Science Through Trading Robots How to get students interested in algorithms, combinatorial optimization and software development Karl Lieberherr, Northeastern University, Boston SDG Mittagsseminar 1

Outline • Specker Derivative Game (SDG) – history – example, bottom up – top-down • derivatives, raw materials, finished products • • Risk analysis for a derivative Problem reductions – noise elimination SDG(MAX-SAT): risk analysis using polynomials Conclusions SDG Mittagsseminar 2

History • Around 1975: working on non-chronological backtracking for MAX-SAT for my Ph. D with Erwin Engeler. • Ernst Specker analyzed MAX-SAT which lead to the Golden Ratio Result: joint FOCS 79 and JACM 1981 paper. Ideas applicable to MAX-CSP. • 2006: sabbatical at Novartis reactivated my interest in MAX-SAT. • 2007: Turned Golden Ratio Result into a game SDG(Max) parameterized by a maximization problem Max. • 2007/2008: Taught SDG to students who had a lot of fun trying to produce a winning robot (class size 30). SDG Mittagsseminar 3

SDG Example • • derivative(CNF{(2, 0), (1, 1)}, 0. 70) 4 variables maximum would you like to buy it? you will get two rights – you will receive a CNF R of the given type. – if you can satisfy fraction q of clauses in R, I will pay back q to you. CNF = SEQUENCE of clauses SDG Mittagsseminar 4

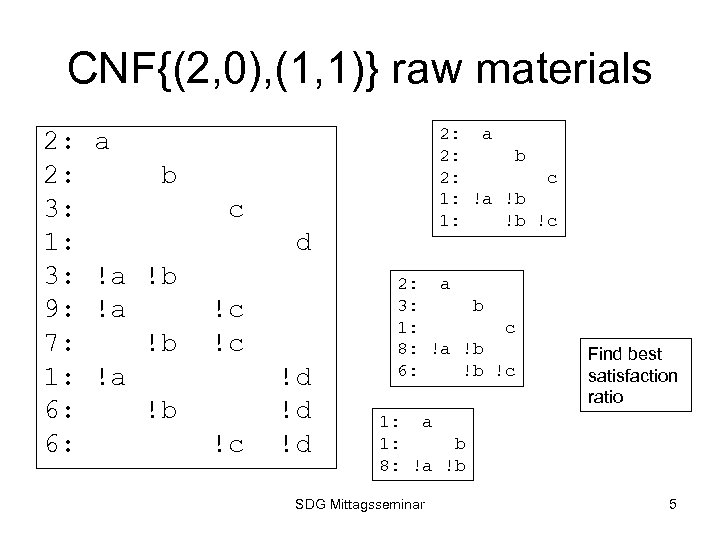CNF{(2, 0), (1, 1)} raw materials 2: 2: 3: 1: 3: 9: 7: 1: 6: 6: 2: a 2: b 2: c 1: !a !b 1: !b !c a b c d !a !b !c !c !c !d !d !d 2: a 3: b 1: c 8: !a !b 6: !b !c Find best satisfaction ratio 1: a 1: b 8: !a !b SDG Mittagsseminar 5

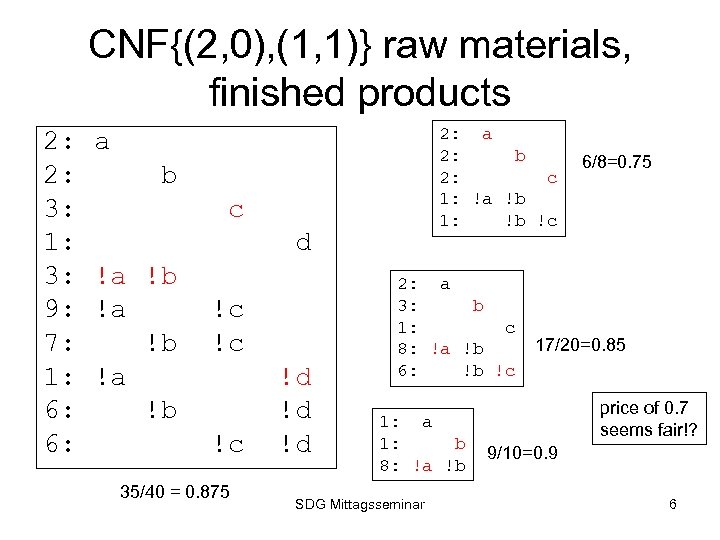CNF{(2, 0), (1, 1)} raw materials, finished products 2: 2: 3: 1: 3: 9: 7: 1: 6: 6: 2: a 2: b 2: c 1: !a !b 1: !b !c a b c d !a !b !c !c !c 35/40 = 0. 875 !d !d !d 2: a 3: b 1: c 8: !a !b 6: !b !c 1: a 1: b 8: !a !b SDG Mittagsseminar 6/8=0. 75 17/20=0. 85 price of 0. 7 seems fair!? 9/10=0. 9 6

Oops • Our analysis was not thorough enough! • 2 kinds of uncertainty: – worst formula? – best assignment? SDG Mittagsseminar 7

Playing with the weights x: x: y: y: y: a b c d !a !b x = 2, y=1 best assignment a=1, b=1, c=0, d=0: (4+5)/14=9/14=0. 64 !c !c !c x =1, y=1 best assignment a=1, b=0, c=0, d=0: (1+6)/10=7/10=0. 7 !d !d !d derivative(CNF{(2, 0), (1, 1)}, 0. 70) LOSS: 0. 06 SDG Mittagsseminar 8

The SDG Game: Two high level views • Financial: Implement trading robots that survive in an artificial derivative market through offering derivatives, and buying and processing derivatives produced by other trading robots. • Biological: Implement organisms that survive in an artificial world through offering outsourced services, and consuming and processing outsourced services produced by other organisms. SDG Mittagsseminar 9

Derivative: (pred, p, s) bought by b • Max is an NP-hard combinatorial maximization problem with objective function range [0, 1]. • Buyer b buys derivative at price p. • Seller s delivers raw material R (instance of Max) satisfying predicate pred. • Raw material R is finished by buyer with outcome O of quality q and seller pays q to buyer. • Buyer only buys if she thinks q > p. • Uncertainty for buyer: which raw material R will I get? Only know the predicate! What is the quality of the solution of Max I can achieve for R? SDG Mittagsseminar 10

Buyer b Seller s (pi, p, s) SDG Mittagsseminar 11

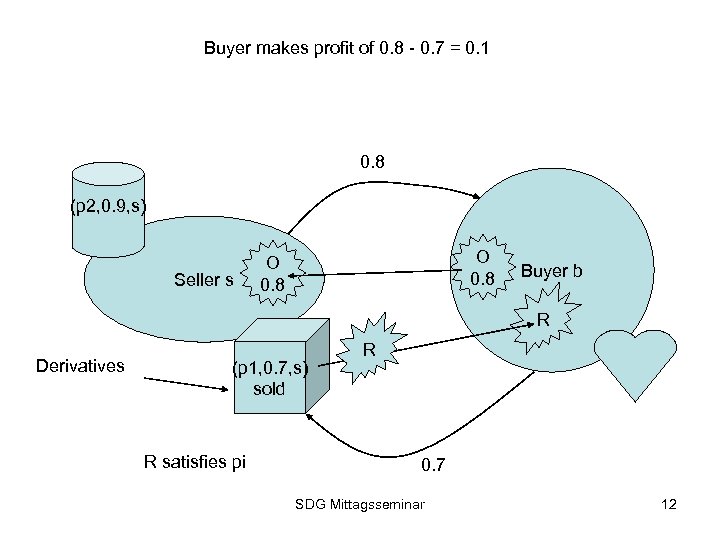Buyer makes profit of 0. 8 - 0. 7 = 0. 1 0. 8 (p 2, 0. 9, s) Seller s O 0. 8 Buyer b R Derivatives (p 1, 0. 7, s) sold R satisfies pi R 0. 7 SDG Mittagsseminar 12

Artificial markets • Trading Robots that survive in a virtual world of an artificial market of financial derivatives. – Trading Robots that don’t follow the world rules don’t survive. – Trading Robots are ranked based on their bank account. – Teaches students about problem solving, software development, analyzing and approximating combinatorial maximization problems, game design and financial derivatives. SDG Mittagsseminar 13

Survive in an artificial market • Each robot contains a: – – Derivative buying agent Derivative offering agent Raw material production agent Finished product agent (solves Max) • Winning in robot competitions strongly influences the final grade. • Game is interesting even if robots are far from perfect. • Focus today: how to play the game perfectly (never losing) SDG Mittagsseminar 14

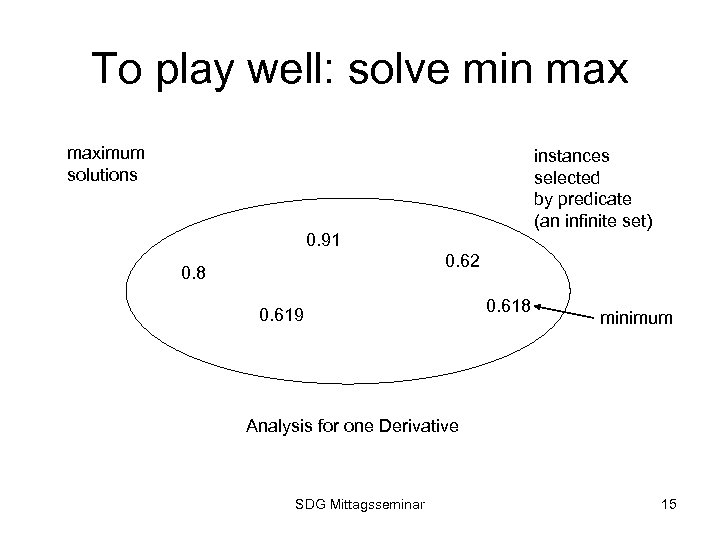To play well: solve min maximum solutions instances selected by predicate (an infinite set) 0. 91 0. 62 0. 8 0. 619 0. 618 minimum Analysis for one Derivative SDG Mittagsseminar 15

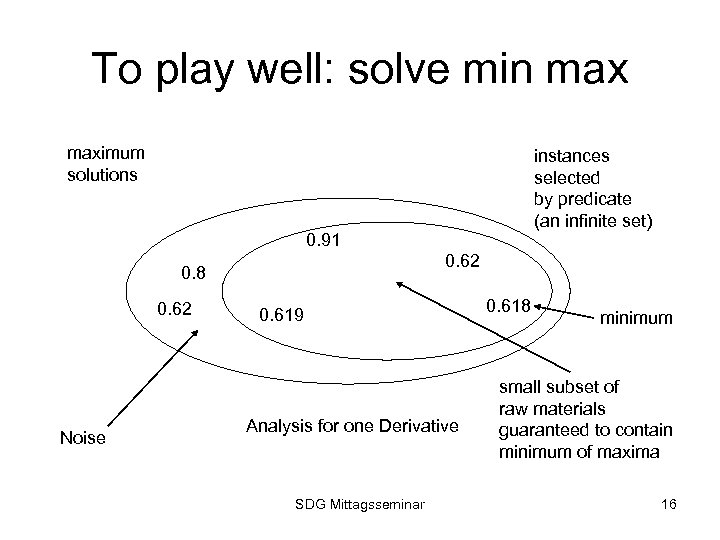To play well: solve min maximum solutions instances selected by predicate (an infinite set) 0. 91 0. 62 0. 8 0. 62 Noise 0. 619 Analysis for one Derivative SDG Mittagsseminar 0. 618 minimum small subset of raw materials guaranteed to contain minimum of maxima 16

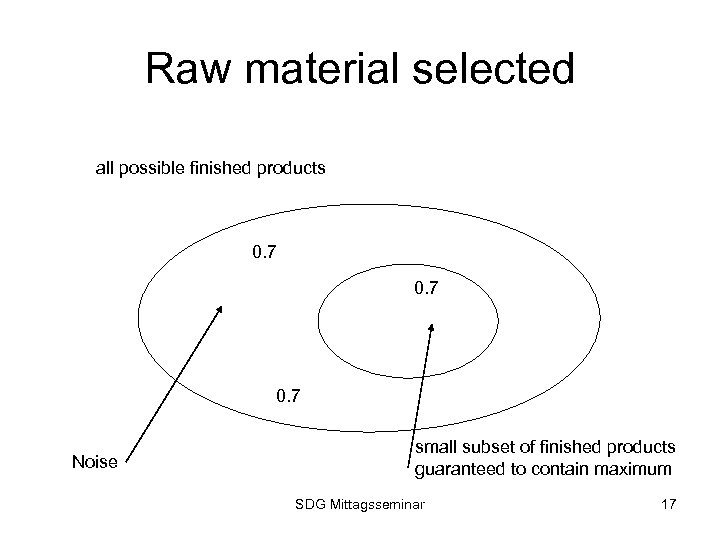Raw material selected all possible finished products 0. 7 Noise small subset of finished products guaranteed to contain maximum SDG Mittagsseminar 17

Risk analysis • Life cycle of a derivative (pred, p) – offer • risk high if I can find rm and fp with q(fp) > p – buy • risk high if I can find rm and fp with q(fp) < p – raw material (rm) – finished product (fp , quality q(fp)) • Two uncertainties – raw material is not the worst (uncertainty_rm) – finished product is not the best (uncertainty_fp) SDG Mittagsseminar 18

To play SDG perfectly eliminate risk • buy – break-even price • sell – break-even price • produce – efficiently find worst case example • process – efficiently achieve break-even quality SDG Mittagsseminar 19

Goal: never lose with offer/buy • Choose algorithms RM and FP SDG Mittagsseminar 20

Concerns for SDG(Max) • Robot communication – exchange language for derivatives, raw material, finished product – centralized game with administrator managing store of derivatives – decentralized game • Winning in the market – clever algorithm design SDG Mittagsseminar 21

Analysis of SDG(Max) tpred = inf all raw materials rm satisfying predicate pred max all finished products fp produced for rm q(fp) SDG Mittagsseminar 22

Analysis of SDG(Max) tpred = lim n -> ∞ min all raw materials rm of size n satisfying predicate pred max all finished products fp produced for rm q(fp) SDG Mittagsseminar 23

Spec for RM and FP tpred = lim n -> ∞ min all raw materials rm of size n satisfying predicate pred and having property WORST(rm) max small subset of all finished products fp produced for rm q(fp) SDG Mittagsseminar 24

Analysis of SDG(Max) tpred = lim n -> ∞ min all raw materials rm of size n produced by RM satisfying predicate pred max all finished products fp produced for rm by FP q(fp) SDG Mittagsseminar 25

Hope • Max is NP-hard • SDG(Max) simplifies Max if our goal is to never lose. SDG Mittagsseminar 26

SDG(MAX-SAT) • Predicates using clause types. • Example predicate Pair. Sat = All CNFs with clauses of any length but clauses of length 1 must contain one positive literal. • What is the right price p for derivative (Pair. Sat, p, Specker) SDG Mittagsseminar 27

SDG(MAX-SAT) • Predicate space: any subset of clause types of Pair. Sat • t all Pair. Sat = (√ 5 -1)/2 • t {(2, 0), (1, 1)} = (√ 5 -1)/2 • t {(100, 50), (3, 2), (2, 0), (1, 1)} = (√ 5 -1)/2 Noise for the purpose of constructing raw material. SDG Mittagsseminar 28

SDG(MAX-SAT) • t {(2, 0), (1, 1)} = t SYM{(2, 0), (1, 1)} = (√ 5 -1)/2 • SYM stands for Symmetrization: Idea: if you give me a CNF with a satisfaction ratio f, I give you a symmetric CNF with a satisfaction ratio <= f. • For a CNF in SYM{(2, 0), (1, 1)}, the MAXSAT problem reduces to maximizing a polynomial. SDG Mittagsseminar 29

Students implement trading robots • Fall semester (undergraduates): SDG(MAX-SAT) • Spring semester (graduates): SDG(MAXCSP) – Predicate space: Any subset of Boolean relations of rank 3 • CSP({22}, 4/9, robot 1) • CSP({17, 22}, 1/2, robot 2) SDG Mittagsseminar 30

Opportunities for learning Example SDG(MAX-SAT) • Abstraction: What is important to play the game well. – Game reductions: To play game SDG(MAXSAT) well, it is sufficient to play game SDG(X) well, where X is simpler than MAX-SAT. SDG Mittagsseminar 31

Complexity theory connection • Break-even prices are not only interesting for the SDG game. • They also have complexity-theoretic significance: they are critical transition points separating P from NP (for “most” predicates). SDG Mittagsseminar 32

General Dichotomy Theorem MAX-CSP(G, f): For each finite set G of relations there exists an algebraic number t. G 1 For f ≤ t. G: MAX-CSP(G, f) has polynomial solution For f ≥ t. G+ e: MAX-CSP(G, f) is NP-complete, e>0. hard (solid) NP-complete t. G = critical transition point 0 polynomial solution: Use optimally biased coin. Derandomize. P-Optimal. easy (fluid) Polynomial due to Lieberherr/Specker (1979, 1982) SDG Mittagsseminar 33

Other break-even prices (Lieberherr/Specker (1982)) • G = {R 0, R 1, R 2, R 3}; Rj : rank 3, exactly j of 3 variables are true. t. G= ¼ SDG Mittagsseminar 34

Other break-even prices (Lieberherr/Specker (1982)) • G(p, q) = {Rp, q = disjunctions containing at least p positive or q negative literals (p, q≥ 1)} – Let a be the solution of (1 -x)p=xq in (0, 1). t. G(p, q)=1 -aq SDG Mittagsseminar 35

Lessons learned from SDG • Developing trading robots and make them survive in an artificial market is very motivating to students • Students learn experientially about many important topics driven by the single goal of making their robots competitive – – – software development problem solving by reduction (noise reduction) combinatorial optimization game design sub-optimal playing is very educational too! SDG Mittagsseminar 36

Noise reduction: important topic • seen in solving minimization and maximization problems • To implement trading robots, we use a tool called Demeter. F which is good at noise reduction during programming process: focus on important classes and eliminate noise classes SDG Mittagsseminar 37

Conclusions • SDG(Max) is an interesting tool for teaching a wide variety of topics. • It helps if you give your students a robot that knows the basic rules. Then the students can focus on improving the robots rather than getting all robots to communicate properly. SDG Mittagsseminar 38

Conclusions • SDG(Max) is an interesting tool for research. • Does it always turn an NP-hard maximization problem into a polynomial time approximation algorithm? SDG Mittagsseminar 39

References • Lieberherr/Specker (1979, 1981) FOCS and Journal of the ACM • Lieberherr (1982) Journal of Algorithms • Recent Workshop paper: – Christine D. Hang and Ahmed Abdelmeged and Daniel Rinehart and Karl J. Lieberherr, The Promise of Polynomial-based Local Search to Boost Boolean MAX-CSP Solvers, 2007, Proceedings of Fourth International Workshop on Local Search Techniques in Constraint Satisfaction, CP 2007, Providence, Rhode Island. • Demeter. F home page: http: //www. ccs. neu. edu/research/demeter/Demeter. F/ • SDG home page: http: //www. ccs. neu. edu/home/lieber/evergreen/specker/s dg-home. html SDG Mittagsseminar 40

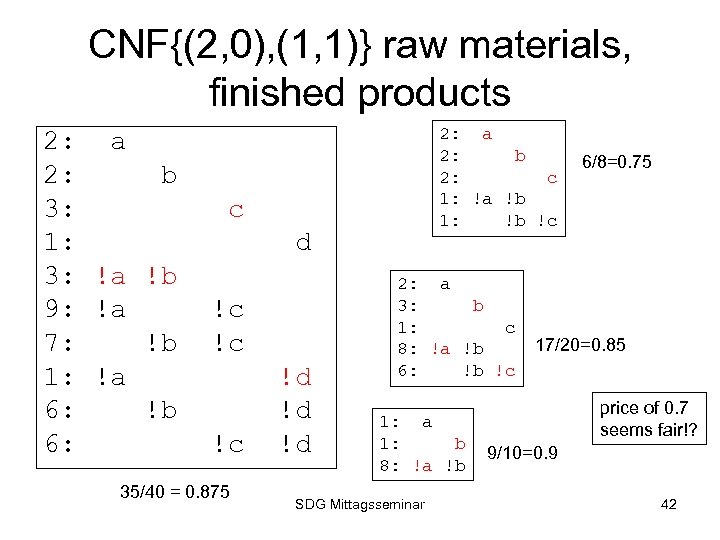
Obstacles to finding p • Try to find a CNF satisfying Pair. Sat in which only a small percentage of the clauses can be satisfied. – Challenge of finding the worst case. – Even if we find the worst case, we might not find the maximum assignment for that case. SDG Mittagsseminar 41

CNF{(2, 0), (1, 1)} raw materials, finished products 2: a 2: b 3: 1: 3: !a !b 9: !a 7: !b 1: !a 6: !b 6: 2: a 2: b 2: c 1: !a !b 1: !b !c c d !c !c !c 35/40 = 0. 875 !d !d !d 2: a 3: b 1: c 8: !a !b 6: !b !c 1: a 1: b 8: !a !b SDG Mittagsseminar 6/8=0. 75 17/20=0. 85 price of 0. 7 seems fair!? 9/10=0. 9 42

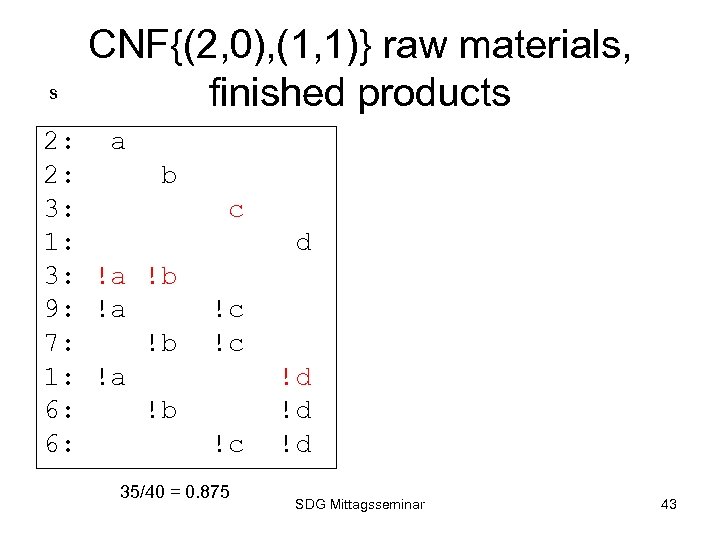s CNF{(2, 0), (1, 1)} raw materials, finished products 2: a 2: b 3: 1: 3: !a !b 9: !a 7: !b 1: !a 6: !b 6: c d !c !c !c 35/40 = 0. 875 !d !d !d SDG Mittagsseminar 43

T(s) 2: 2: 3: 1: 3: 9: 7: 1: 6: 6: CNF{(2, 0), (1, 1)} reduction a !b !a b a !a !b !b no new variables !c !d c c !c !c 35/40 = 0. 875 d !d To each interpretation I 1 of T(s) corresponds an interpretation I of s which satisfies at least as many clauses in s as I 1 in T(s). !d !d !d SDG Mittagsseminar 44

CNF{(2, 0), (1, 1)} reduction 2: 2: 3: 1: 3: 9: 7: 1: 6: 6: a !b !a b a !a !b !b no new variables !c !d c c !c !c 35/40 = 0. 875 d !d To each interpretation I 1 of T(s) corresponds an interpretation I of s which satisfies at least as many clauses in s as I 1 in T(s). !d !d !d SDG Mittagsseminar 45

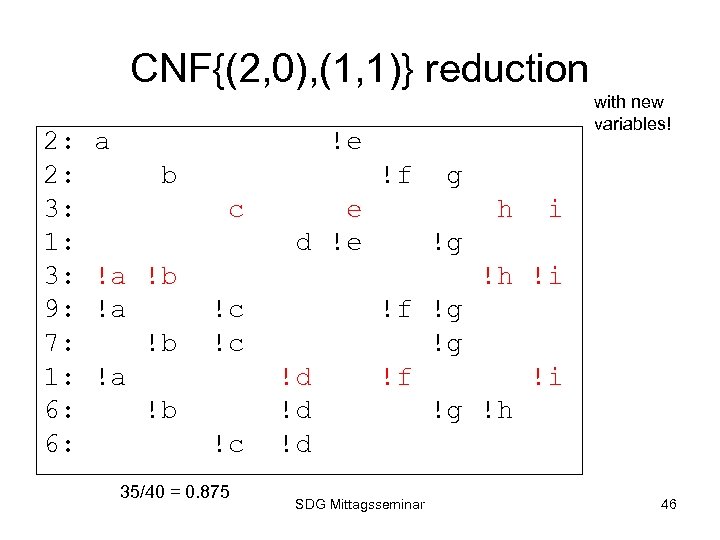CNF{(2, 0), (1, 1)} reduction 2: 2: 3: 1: 3: 9: 7: 1: 6: 6: a with new variables! !e b !f c !a !b e d !e g h i !g !h !i !c !c !c 35/40 = 0. 875 !d !d !d !f !g !g !f !i !g !h SDG Mittagsseminar 46

SDG(Max) • Derivative = (Predicate, Price in [0, 1], Player). • Players offer and buy derivatives. • Buying a derivative gives you the rights: – to receive raw material R satisfying the predicate. – upon finishing the raw material R at quality q (trying to find the maximum solution), you receive q in [0, 1]. SDG Mittagsseminar 47

• 18. Juli 18. 00 Steinbruechelstr. 45 • Edi Zehnder SDG Mittagsseminar 48

After talk • Discussion with Emo • break-even price as Nash equilibrium • 2 person zero sum game – distribution on clauses – distribution on assignments SDG Mittagsseminar 49

SDG(Max) • not percentage of all but percentage of maximum. • approximation: seller knows a good solution for raw material. If buyer achieves SDG Mittagsseminar 50

• derivative = (predicate, p, robot) • p = price = estimate how close I can get to the maximum • problem = knowing exact maximum is hard • approximation: p = price = estimate how close I can get to the outcome the seller knows for an instance satisfying the predicate. SDG Mittagsseminar 51

• payoff: seller achieves with outcome O quality q(O). • I achieve • seller: 18, price 15/18 • I: 15: paid back 15/18 • I: 16: paid back 14/18 • I: 100: paid back 100/18 SDG Mittagsseminar 52

• still flavor of derivatives • (pred, p, r) p is estimate how well I can solve an instance satisfying pred compared to how well r can solve it. r has more time available. Here don’t need assumption that objective function in [0, 1]. • now: p is an estimate how well I can solve an instance satisfying pred compared to 1. SDG Mittagsseminar 53

cryptography • Emo’s satisfiability class: 4 algorithms for 2 -Sat. For my algorithms class? • r knows good solution. If I would know this good solution, could break system. • any approximation would not be useful. Price would have to be 1 SDG Mittagsseminar 54

• SDG(CNF-ALL) • SDG(CNF-MAX) uninteresting: eval is exponential • SDG(CNF-SECRET) – owner delivers with rm a number f. – seller, after receiving fp, delivers outcome satisfying f – if buyer achieves f * price or higher, buyer receives 1, otherwise 0. all-or-nothing. Can buyer discover the secret that was put into instance by seller? – problem: price of 1 not interesting. Discount? Buyer only pays 0. 9 * f. SDG Mittagsseminar 55

discount idea • works also with SDG(CNF-ALL) • price is p, but pay only 0. 9*p. More realistic. Pay only 0. 9, 0. 1 is for effort. • Use all or nothing. discount = d SDG Mittagsseminar 56

ABB • Trading Robot development for artificial markets (to illustrate good separation of concerns from design to implementation using a traversalbased, functional implicit invocation architecture) – why trading robot: industrial IT – why good separation of concerns: always helps. – why traversal-based, functional implicit invocation architecture: built-in variability (class graph generic), support for parallelism: exploiting multi-core architecture • Example: Shannon decomposition, testing history of generic SDG game. SDG Mittagsseminar 57

derivative[CSP] = (pred, approx (all, max, secret), robot) price = (1 -d)*approx • global discount d: pay only (1 -d)*approx. • if achieve approx of (all, max, secret): receive 1 otherwise 0. • secret requires extra protocol step. SDG Mittagsseminar 58

derivative[CSP] = (pred, approx (all, secret), robot) price = (1 -d)*approx • global discount d: pay only (1 -d)*approx. • if achieve approx of (all, secret): receive 1 otherwise 0. • secret requires extra protocol step. • (delete max, because evaluation is costly. Game becomes less interesting. ) • good for variant of SDG game SDG Mittagsseminar 59

derivative[Boolean. CSP] = (pred, approx, robot) price = (1 -d)*approx • global discount d: pay only (1 -d)*approx. • d is compensation for effort to produce finished product • if achieve approx of all or more: receive 1 otherwise 0. • good for talk: quick intro. • Use Boolean. CSP because it is clear what all means. SDG Mittagsseminar 60