Усеченный конус Усеченный конус — часть полного

Усеченный конус.

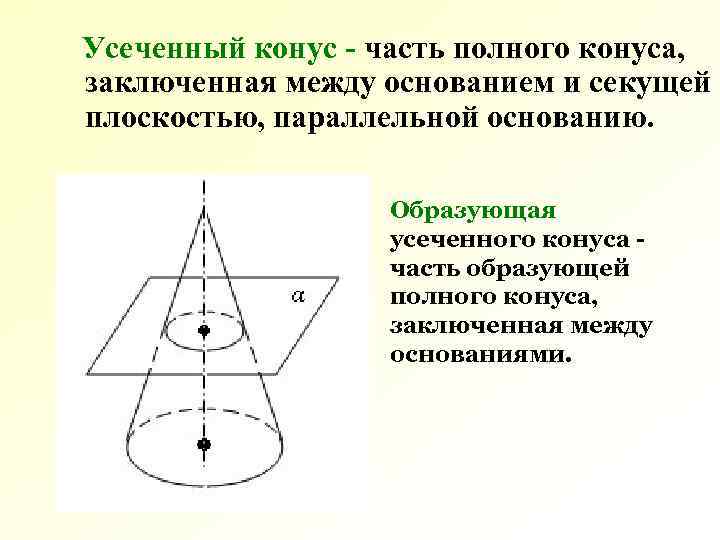Усеченный конус - часть полного конуса, заключенная между основанием и секущей плоскостью, параллельной основанию. Образующая усеченного конуса часть образующей полного конуса, заключенная между основаниями.

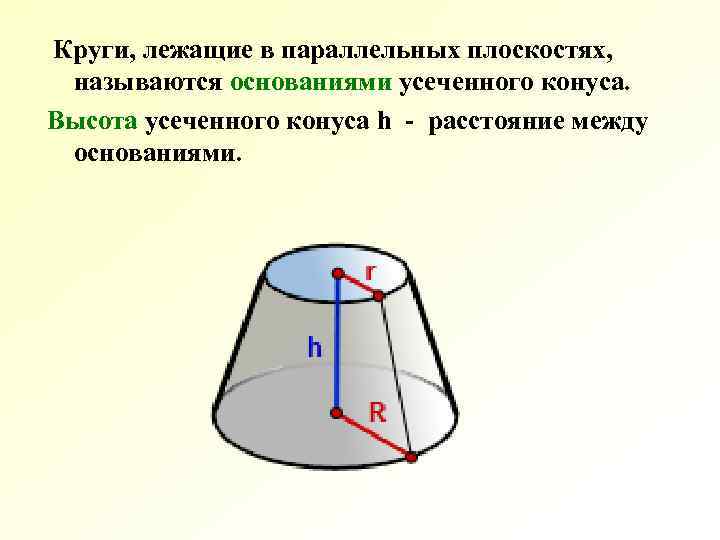Круги, лежащие в параллельных плоскостях, называются основаниями усеченного конуса. Высота усеченного конуса h - расстояние между основаниями.

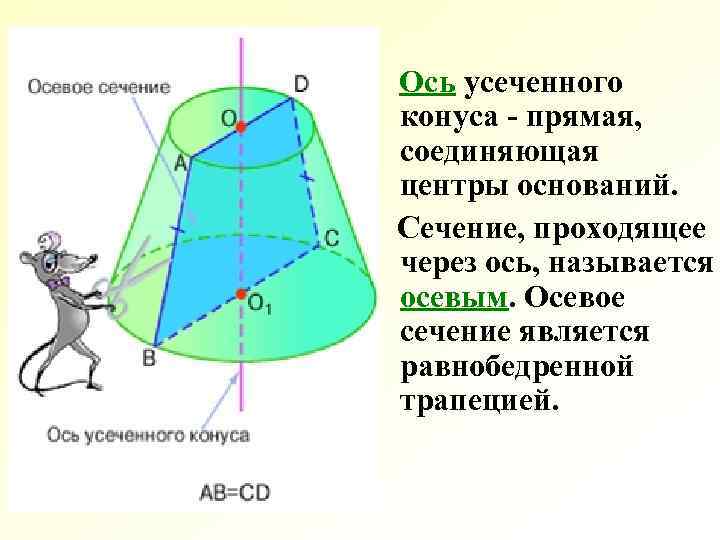Ось усеченного конуса - прямая, соединяющая центры оснований. Сечение, проходящее через ось, называется осевым. Осевое сечение является равнобедренной трапецией.

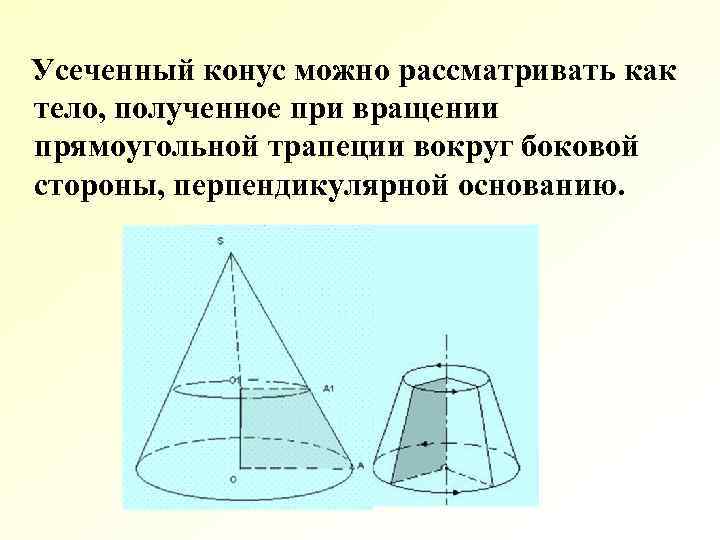Усеченный конус можно рассматривать как тело, полученное при вращении прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию.

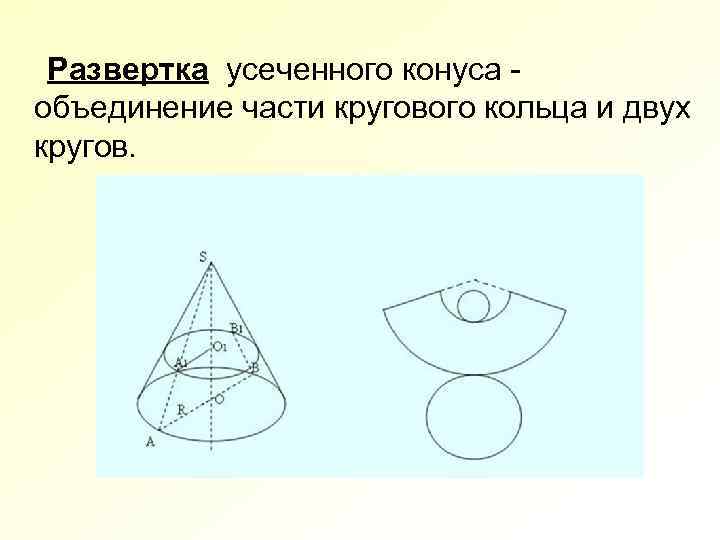Развертка усеченного конуса - объединение части кругового кольца и двух кругов.

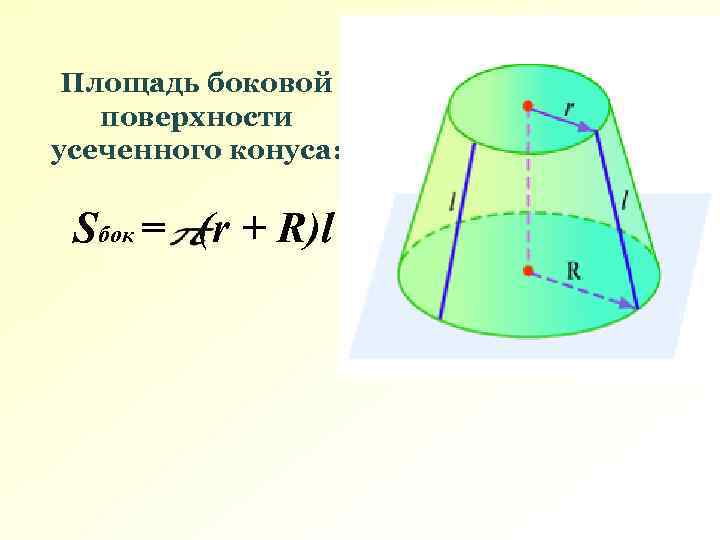Площадь боковой поверхности усеченного конуса: Sбок = (r + R)l

Дано: r – радиус меньшего основания R - радиус большего основания l - образующая Доказать: Sбок= (r + R)l

Доказательство: Впишем в конус правильную пирамиду. Ее боковая поверхность состоит из трапеций.

Площадь полной поверхности усеченного конуса называется сумма площадей его боковой поверхности и основания.

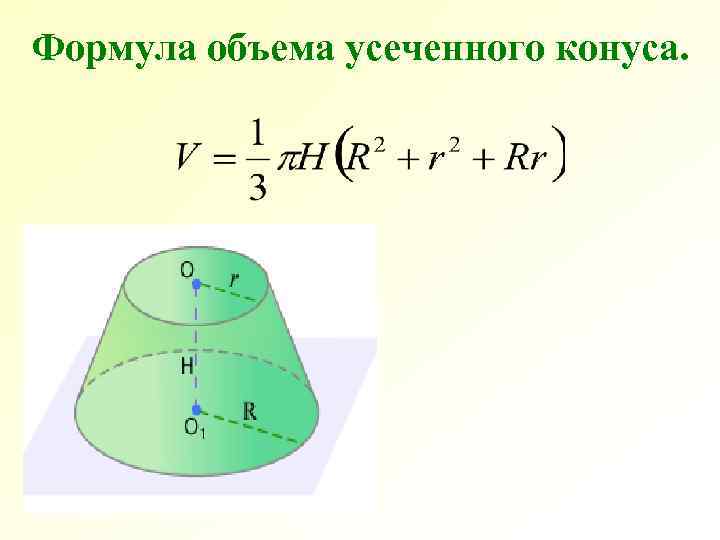Формула объема усеченного конуса.

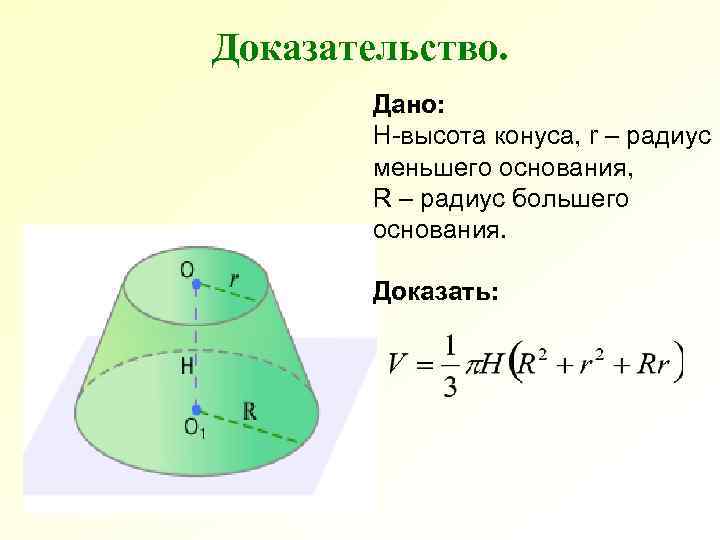Доказательство. Дано: H-высота конуса, r – радиус меньшего основания, R – радиус большего основания. Доказать:

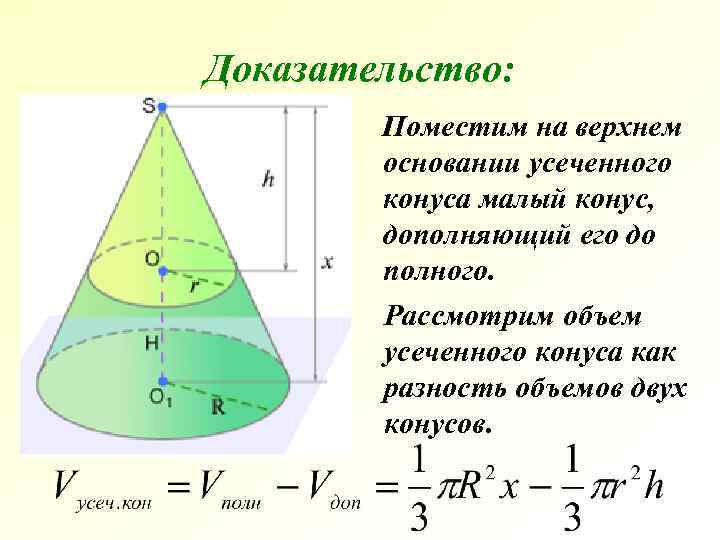Доказательство: Поместим на верхнем основании усеченного конуса малый конус, дополняющий его до полного. Рассмотрим объем усеченного конуса как разность объемов двух конусов.

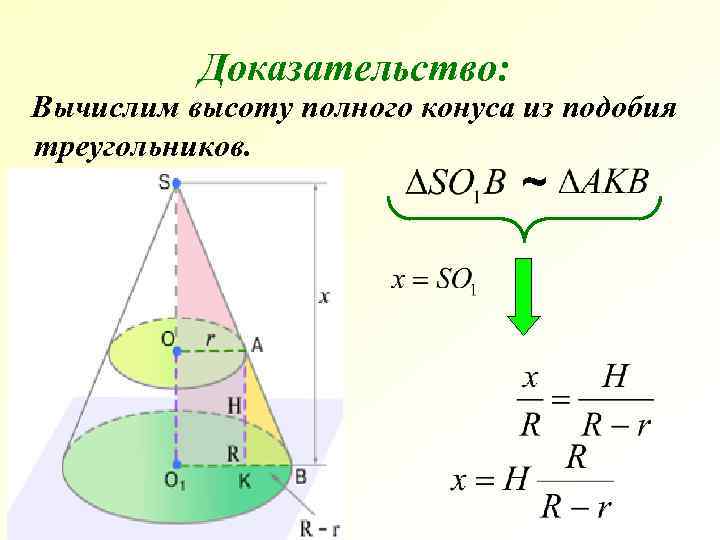Доказательство: Вычислим высоту полного конуса из подобия треугольников. ~

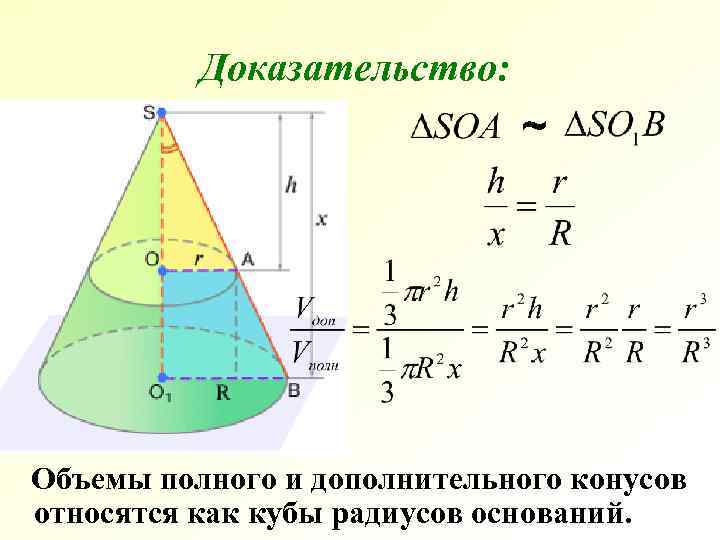Доказательство: ~ Объемы полного и дополнительного конусов относятся как кубы радиусов оснований.

Доказательство: Вычтем из объема большого конуса объем малого конуса.

Площадь сферы радиуса R: Объем шара радиуса R:

Спасибо за внимание.