
Урок з теми “Об’єм конуса” 11 клас

Об’єм конуса Конус— тіло, отримане шляхом об'єднання всіх променів, що виходять з однієї точки — вершини конуса, і таких що проходять через довільну плоску поверхню.
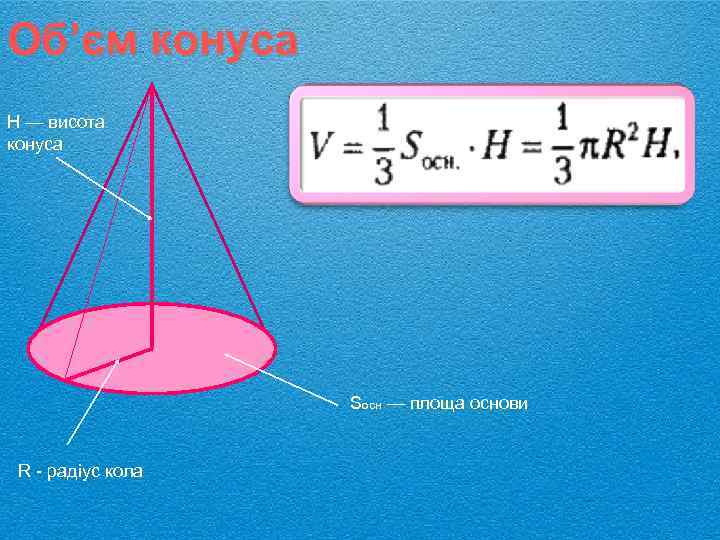
Об’єм конуса Н — висота конуса Sосн — площа основи R - радіус кола

Теорема 31. Об’єм конуса дорівнює одній третині добутку площі його основи на висоту. Н R Основи конуса та зрізаного конуса – круги, а площа куга радіуса r дорівнює πR². Тому об’єм конуса можна обчислити за формулою: де Н - його висота, а R - радіус основи.

Розв’язування задач
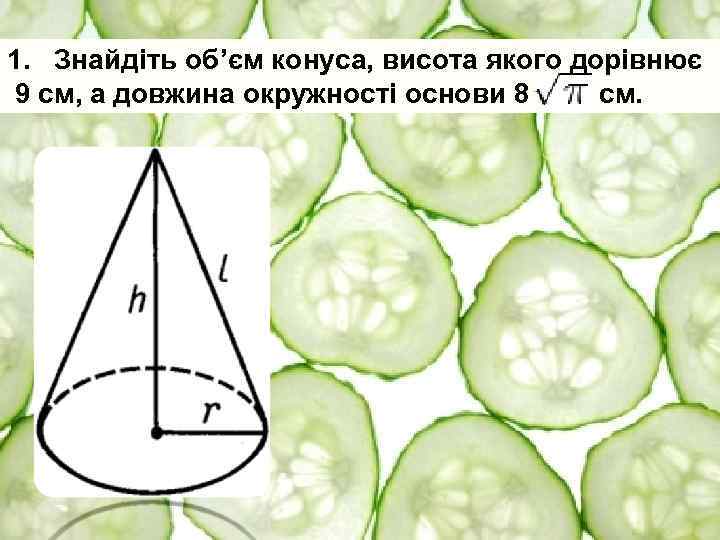
1. Знайдіть об’єм конуса, висота якого дорівнює 9 см, а довжина окружності основи 8 см.

2. Через вершину конуса проведена площина перерізу під кутом 45 до основи. Ця площина перетинає основу по хорді, яка видна із центра основи конуса під кутом 60. Знайдіть об’єм конуса, якщо відстань від центра основи до хорди дорівнює 6 см.
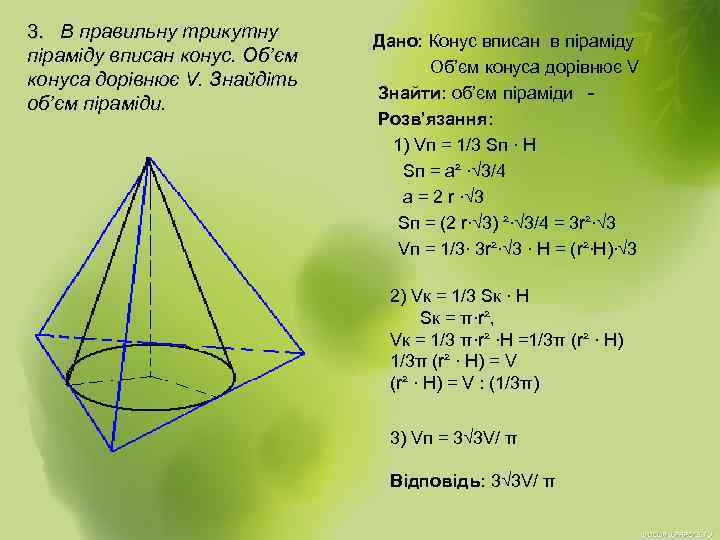
3. В правильну трикутну піраміду вписан конус. Об’єм конуса дорівнює V. Знайдіть об’єм піраміди. Дано: Конус вписан в піраміду Об’єм конуса дорівнює V Знайти: об’єм піраміди Розв’язання: 1) Vп = 1/3 Sп ∙ H Sп = а² ∙√ 3/4 а = 2 r ∙√ 3 Sп = (2 r∙√ 3) ²∙√ 3/4 = 3 r²∙√ 3 Vп = 1/3∙ 3 r²∙√ 3 ∙ H = (r²∙H)∙√ 3 2) Vк = 1/3 Sк ∙ H Sк = π∙r², Vк = 1/3 π∙r² ∙H =1/3π (r² ∙ Н) = V : (1/3π) 3) Vп = 3√ 3 V/ π Відповідь: 3√ 3 V/ π

4. В конус вписана правильна трикутна піраміда. Об’єм конуса дорівнює V. Знайдіть об’єм піраміди. Дано: Пирамида вписана в конус Об’єм конуса равен V Знайти: об’єм піраміди Розв’язання: 1) Vп = 1/3 Sп ∙ H Sп = а² ∙√ 3/4 а = R ∙√ 3 Sп = (R∙√ 3) ²∙√ 3/4 = 3 R²∙√ 3/4 Vп = 1/3∙ 3 R²∙√ 3/4 ∙ H = (R²∙H)∙√ 3/4 2) Vк = 1/3 Sк ∙ H Sк = π∙R², Vк = 1/3 π∙R² ∙H =1/3π (R²∙ Н) 1/3π (R² ∙ Н) = V : (1/3π) 3) Vп = 3√ 3 V/ 4π Відповідь: 3√ 3 V/ 4π