Урок-практикум по теме Нестандартные методы решения уравнений и

Урок-практикум по теме "Нестандартные методы решения уравнений и неравенств"

Цель – обучение учащихся решению уравнений и неравенств за счет глубокого понимания теоретических основ, применяемых в математике. Задачи, решаемые в процессе обучения: развить нестандартное мышление учащихся; сформировать умение строить математические модели; отработать навыки прохождения тестирования при подготовке к ЕГЭ (решение задач повышенной сложности); повысить интерес к математике; привить уверенность учащимся при решении задач

Повторение 1. Как решаются уравнения вида? 2. Как решаются уравнения вида? 3. Как решаются логарифмические уравнения с разными основаниями? 4. Как решаются уравнения, в которых фигурирует функция вида ?

Повторение 1. Как решаются уравнения вида? f(x)=(g(x))^2 g(x)>=0 2. Как решаются уравнения вида? 3. Как решаются логарифмические уравнения с разными основаниями? 4. Как решаются уравнения, в которых фигурирует функция вида ?

Повторение 1. Как решаются уравнения вида? f(x)=(g(x))^2 g(x)>=0 2. Как решаются уравнения вида? f(x)=g(x) или f(x)=g(x) f(x)>=0 3. Как решаются логарифмические уравнения с разными основаниями? 4. Как решаются уравнения, в которых фигурирует функция вида ? g(x)>=0

Повторение 3. Как решаются логарифмические уравнения с разными основаниями? 4. Как решаются уравнения, в которых фигурирует функция вида ?

Повторение 3. Как решаются логарифмические уравнения с разными основаниями? 4. Как решаются уравнения, в которых фигурирует функция вида ? F(x)= y F(x)≠y y>0 F(x)≠y y≤ 0 g(x) =logf(x)y Решений нет g(x) = 1

Проблемное задание (работа в группах), задание лежит на каждой парте на листочках. 1. Решите уравнение Решение уже на этом этапе понятно, что решение будет очень громоздко. Возникла проблема - решать это уравнение дальше или искать другой способ решения?

- т. к. логарифмируемые выражения для всех х больше 1, то каждый логарифм – положительное или равное 0 число. - чтобы сумма была равна 0, необходимо складывать нули или числа противоположные, поэтому каждый логарифм может принимать только значение равное нулю, т. е. : Итак, делаем вывод, что уравнения можно решить с помощью использования свойств функции.

Для самостоятельного решения: Решите уравнение: Решение: левая часть уравнения – функция монотонно убывающая, а правая – постоянная, следовательно, уравнение имеет единственный корень х=1 (легко подбирается).

Для решения большинства уравнений и неравенств, встречающихся на экзаменах, в частности на ЕГЭ, достаточно владеть школьным курсом математики, но при этом необходимо уметь их решать не только с помощью стандартных приемов, но и с помощью “нестандартных приемов и методов”. Вот мы с вами на следующих пяти уроках и будем отрабатывать такие методы и приемы. Вы уже при решении некоторых уравнений умеете применять метод подстановки. Сегодня мы уже узнали, что при решении уравнений можно применять свойства функций.

Теперь мне хочется показать применение свойства ограниченности. 1. Теорема 1. Если и , то уравнение Решите уравнение Перепишем уравнение в виде: Так как равносильно системе: и и , следовательно, данное уравнение Ответ. -1.

Метод оценки Иногда уравнение (неравенство) вида устроено так, что левая и правая части представляют из себя ограниченные функции. В этом случае можно (а иногда и единственно возможно) применить метод «оценивания» правой и левой частей. Особенно этот метод полезен при решении так называемых «смешанных» уравнений и неравенств. Метод оценки основывается на утверждении: если некоторое число n является наибольшим значением функции f(x) и одновременно наименьшим значением функции g(x), то уравнение f(x) = g(x) равносильно системе двух уравнений

Решите уравнение log Стандартным путем решить это уравнение невозможно. Обратим внимание на то, что в левой части под логарифмом выражение всегда больше либо равно единицы, логарифмическая функция с основанием 1/3 - убывает, стало быть –. То есть – левая часть всегда меньше или равна нулю. В правой же части – арифметический квадратный корень, который всегда больше или равен нулю. Отсюда получаем, что равенство возможно только когда обе части уравнения обращаются в нуль. Левая часть равна нулю при x=1 и при x=2, а правая – при x=2 и x=4. Отсюда – единственное решение x=2. При решении подобных задач особенно стоит отметить выделение квадрата двучлена в одной или в обеих частях уравнения (неравенства).

Метод монотонности Если y=f(x) - монотонная функция, то уравнение f(x) = c имеет не более одного корня Пусть функция y=f(x) возрастает на промежутке М, а функция y=g(x) убывает на этом промежутке. Тогда уравнение f(x)=g(x) имеет на промежутке М не более одного корня. Пусть область определения функции f(t) есть промежуток М, и пусть эта функция непрерывна и строго монотонна (т. е. возрастает или убывает) на этом промежутке. Тогда уравнение равносильно системе: При решении уравнений вида f(f(x))=x полезна следующая теорема: Если y=f(x)-монотонно возрастающая (убывающая) функция, уравнения f(x) и f(f(x)) эквивалентны.

Метод монотонности Решите уравнение Решение функций). - возрастающая функция (как сумма двух возрастающих В правой части уравнения – постоянное число. В силу теоремы о корне, уравнение имеет не более одного решения. Очевидно, что х=2 – корень. Ответ: х=2.

Использование области определения функций при решении уравнений и неравенств Рассматривается метод, когда при рассмотрении уравнения или неравенства выясняется, что обе его части определены на некотором множестве, состоящем из одного или нескольких чисел. Этот метод наиболее результативен при решении уравнений и неравенств, в состав которых входят функции: у= у=

Использование области определения функций при решении уравнений и неравенств При решении уравнения или неравенства перенести все члены в левую часть и рассмотреть функцию f (x). Найти её область определения Д (f). При этом: 1). Если Д (f) = , то уравнение или неравенство решений не имеют. 2). Если Д (f) = {а 1; а 2; а 3…. . аn}, то действительные решения данного уравнения и неравенства находятся среди чисел а 1; а 2; а 3…. . аn. Теперь необходимо проверить, какие из данных чисел являются решениями уравнения или неравенства. 3). Если Д (f) = [а; в], то нужно проверить верно ли уравнение или неравенство на концах промежутка и в каждом промежутке, причём, если a < 0, а в > 0, то необходима проверка на промежутках (а; 0) и [0; в).

Пример. Решите уравнение: Решение. Выпишем условия, при которых выражения, входящие в левую часть данного уравнения, имеют смысл: Система решений не имеет. Поэтому и исходное уравнение не имеет решений. Ответ: решений нет.

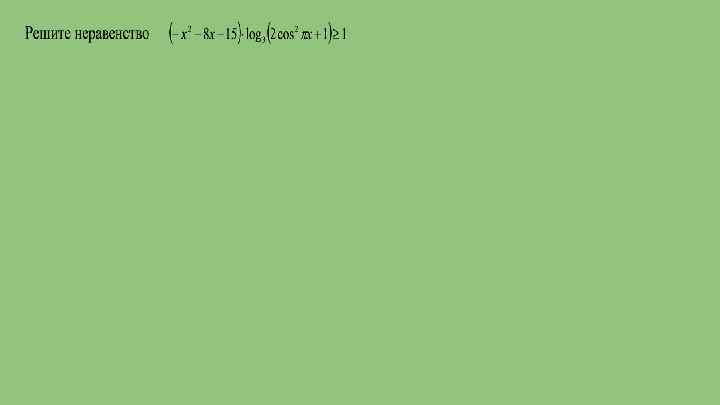
Домашнее задание Решите уравнения и неравенства 1. 2. 3. 4.