Урок геометрии «Вписанный угол»
Устная работа В А О С N М О О K E Дано: АВ : ВС : АС=2: 3: 4 Найти: АОВ, ВОС, АОС Дано: МОN= EOK, MON : NOK : MOE= 3: 4: 5 Найти: МЕ, NK, КЕ.
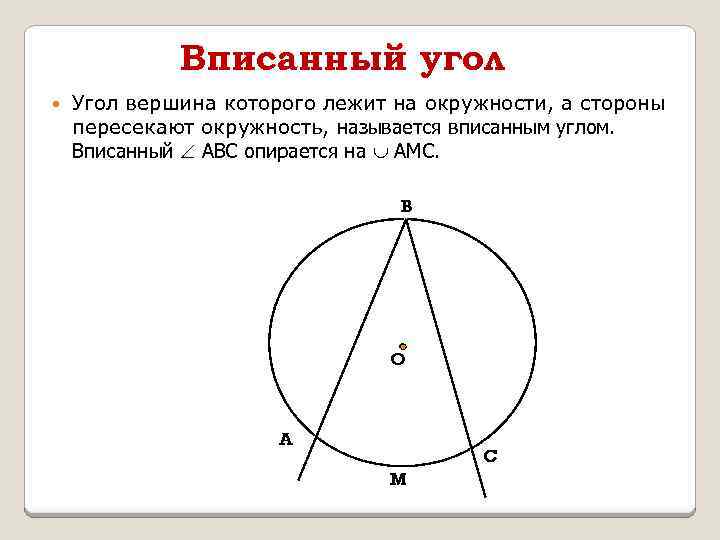
Вписанный угол Угол вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. Вписанный АВС опирается на АМС. B O A C M
ТЕОРЕМА Вписанный угол измеряется половиной дуги на которую он опирается. Пусть АВС – вписанный угол окружности с центром О, опирающийся на АС. Докажем, что АВС = ½ АС. Существует 3 возможных случая расположения луча ВО относительно АВС. Рассмотрим их.
ТЕОРЕМА Вписанный угол измеряется половиной дуги на которую он опирается. B 1 2 Рассмотрим 1 случай: луч ВО совпадает с одной из сторон АВС. O A C АОС= АС, т. к. АОС-центральный. Так как АОС внешний угол р/б АВО, и 1 = 2, то АОС = 1+ 2 = 2 1. Отсюда следует, что 2 1 = АС или 1
ТЕОРЕМА Вписанный угол измеряется половиной дуги на которую он опирается. B O Рассмотрим 2 случай: луч ВО делит АВС на два угла. A C D В этом случае луч ВО пересекает АС в некоторой точке D. Точка D разделяет АС на две дуги: АD и DC. По доказанному в п. 1 АВD = 1/2 AD и DBC= 1/2 DC. Складывая эти равенства попарно, получаем: ABD + DBC = ½ АD + ½ DC = ½ (АD + DC), или
Рассмотрим 3 случай: луч ВО лежит вне АВС В этом случае луч ВС пересекает АD в точке С. Точка С разделяет АD на две дуги: АС и СD. По доказанному в п. 1 АВD = 1/2 AD и СВD= 1/2 СD. Вычитая эти равенства, получаем: АВС= ABD - СВD = ½ АD - ½ СD = ½ (АD - СD) = ½ АС , или B O A C D
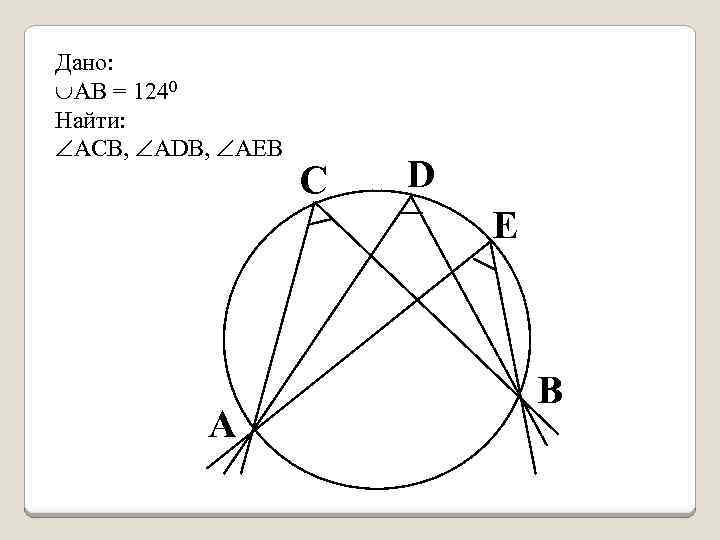
Дано: АВ = 1240 Найти: АCВ, ADВ, АEB С D E А В
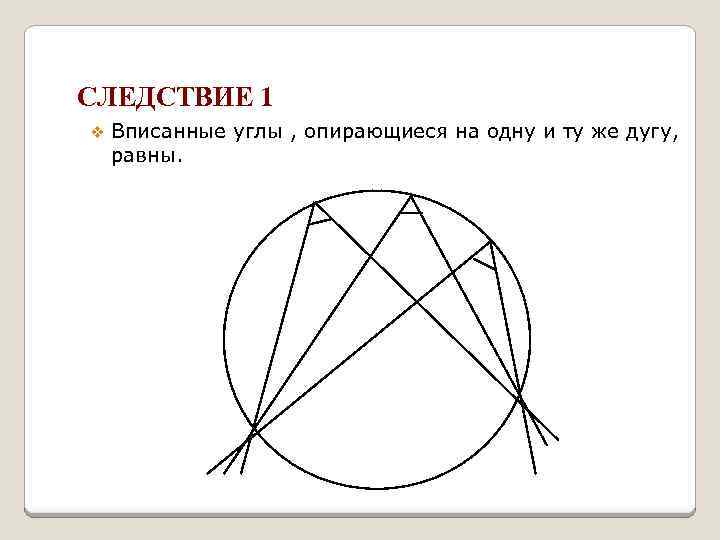
СЛЕДСТВИЕ 1 v Вписанные углы , опирающиеся на одну и ту же дугу, равны.
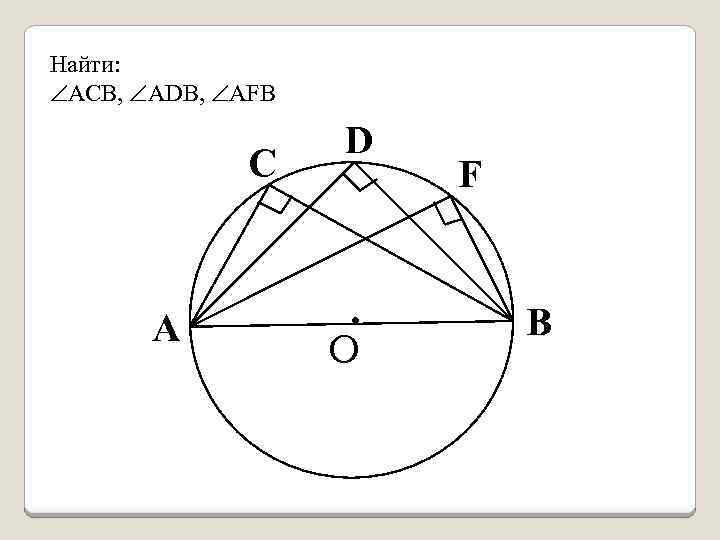
Найти: АCВ, ADВ, АFB C А D . О F B
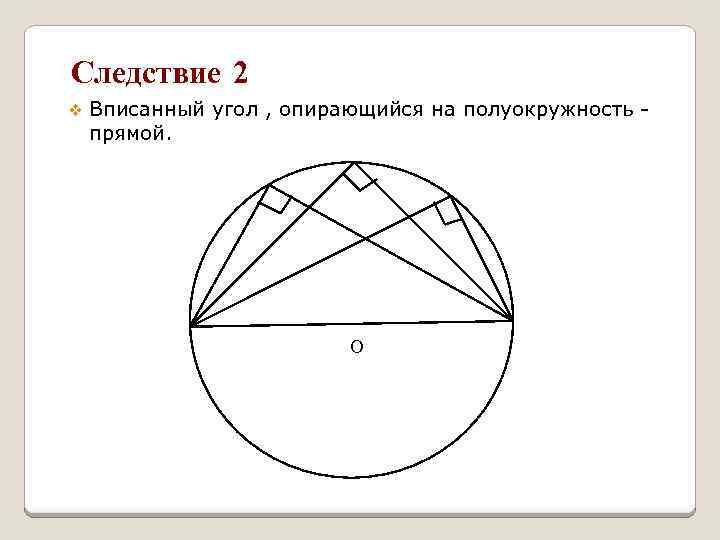
Следствие 2 v Вписанный угол , опирающийся на полуокружность прямой. О
Домашнее задание п. 70, 71, № 653, 654 СПАСИБО за УРОК!
Скачать презентацию Урок геометрии Вписанный угол Устная работа В
17 Вписанный угол.ppt