Урок геометрии в 8 классе по теме Средняя

Урок геометрии в 8 классе по теме «Средняя линия треугольника»

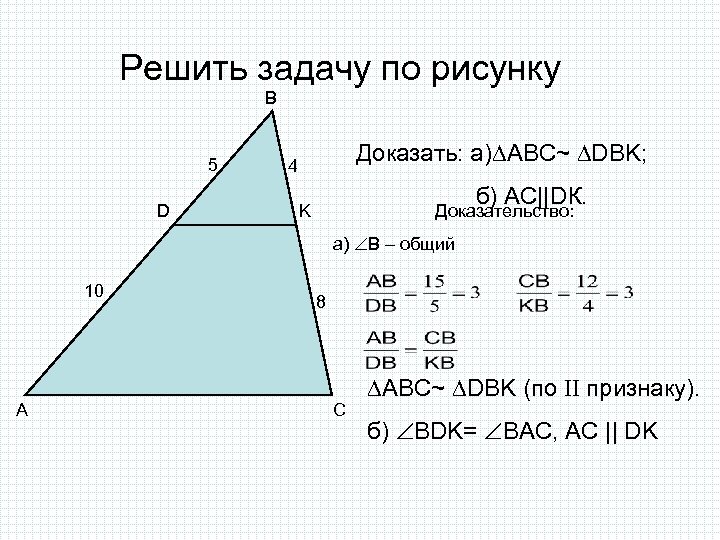Решить задачу по рисунку B 5 D Доказать: а) ABC~ DBK; 4 б) АС||DК. K Доказательство: а) B – общий 10 A 8 C ABC~ DBK (по II признаку). б) BDK= BAC, AC || DK

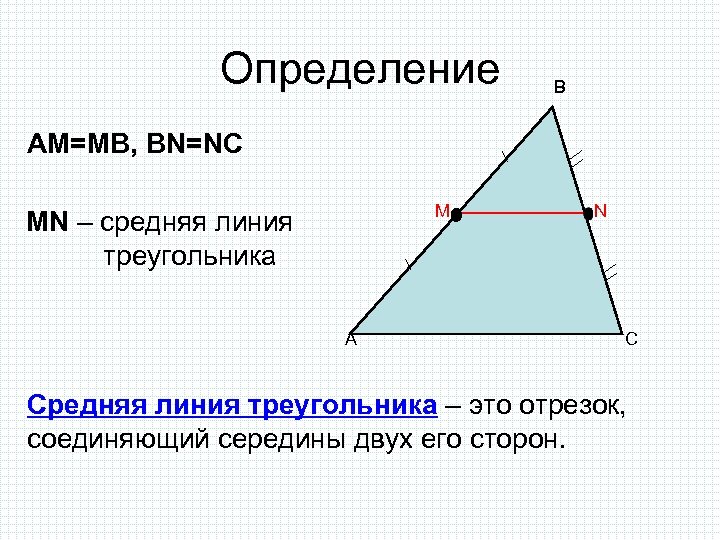Определение B AM=MB, BN=NC M MN – средняя линия треугольника A N C Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.

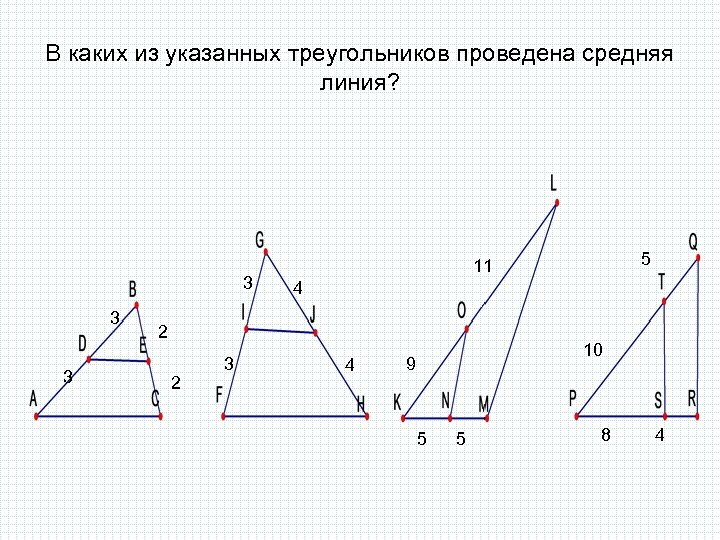В каких из указанных треугольников проведена средняя линия? 3 3 3 4 2 2 3 5 11 4 10 9 5 5 8 4

Теорема о средней линии треугольника B АВС Дано: MN – средняя линия M N Доказать: MN AC, 1 2 MN= AC A C Доказательство: MB NB 1 = = МN – средняя линия АВС AM=MB, BN=NC AB CB 2 B – общий АВС ~ МВN (по II признаку подобия) MN 1 MN = 1 AC = 2 AC 2 BMN= BAC(соответственные) MN AC

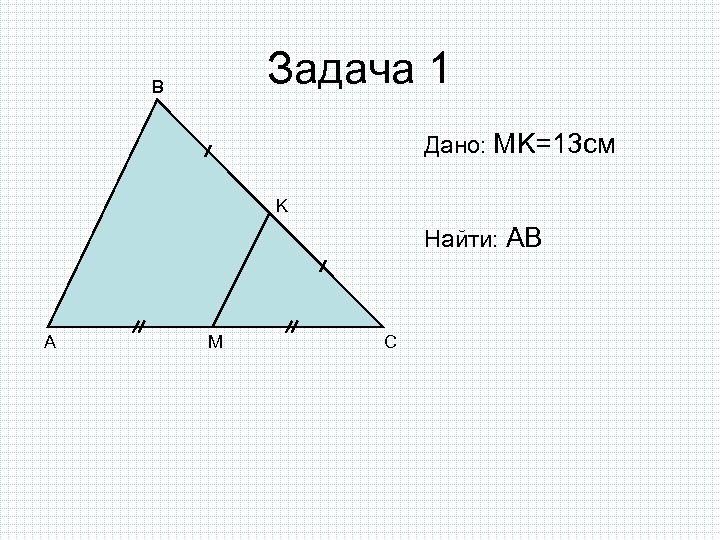Задача 1 B Дано: MK=13 см K Найти: AB A M C

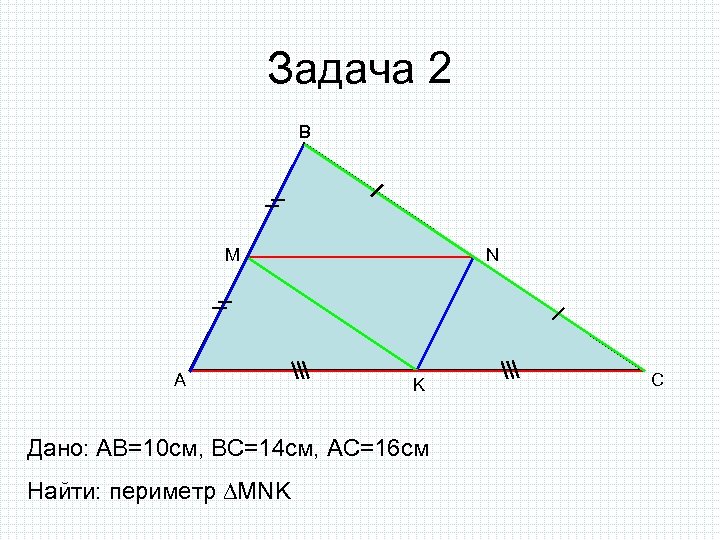Задача 2 B M A N K Дано: AB=10 cм, ВС=14 см, АС=16 см Найти: периметр MNK C

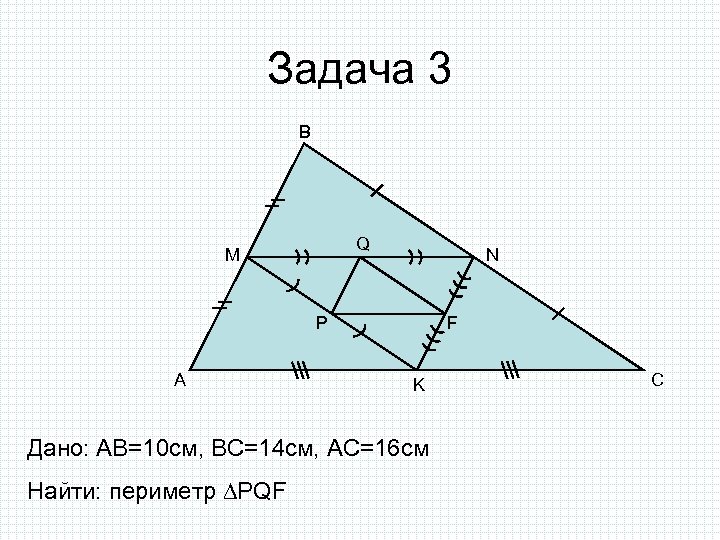Задача 3 B Q M N P A F K Дано: AB=10 cм, ВС=14 см, АС=16 см Найти: периметр PQF C

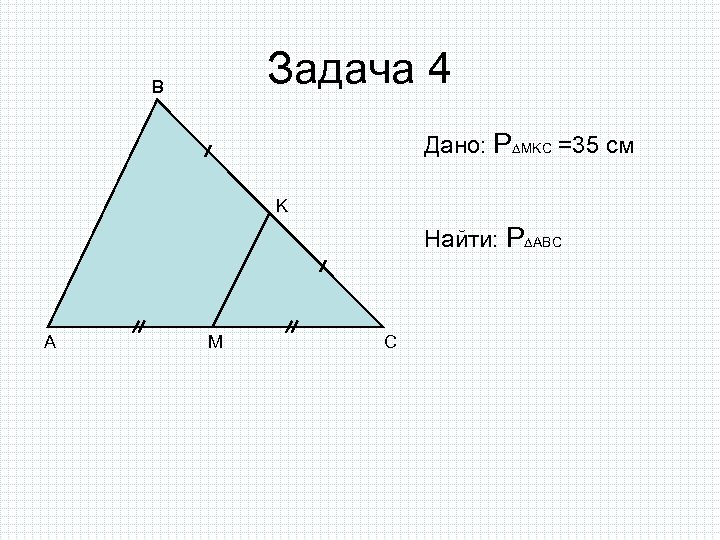Задача 4 B Дано: P MKC =35 см K Найти: P ABC A M C

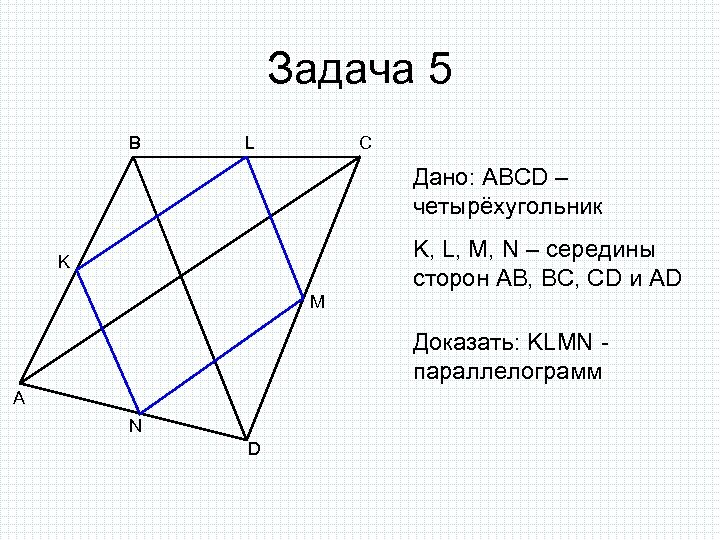Задача 5 B L C Дано: ABCD – четырёхугольник K, L, M, N – середины сторон AB, BC, CD и AD K M Доказать: KLMN параллелограмм A N D

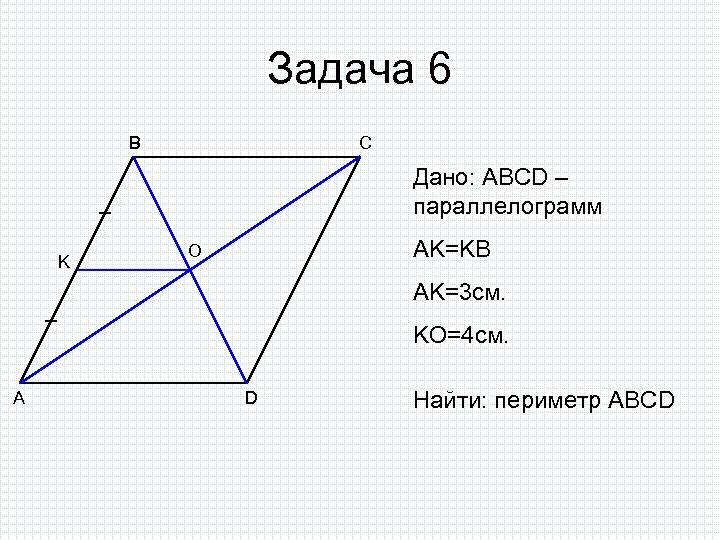Задача 6 B C Дано: ABCD – параллелограмм K AK=KB O AK=3 см. KO=4 см. A D Найти: периметр ABCD

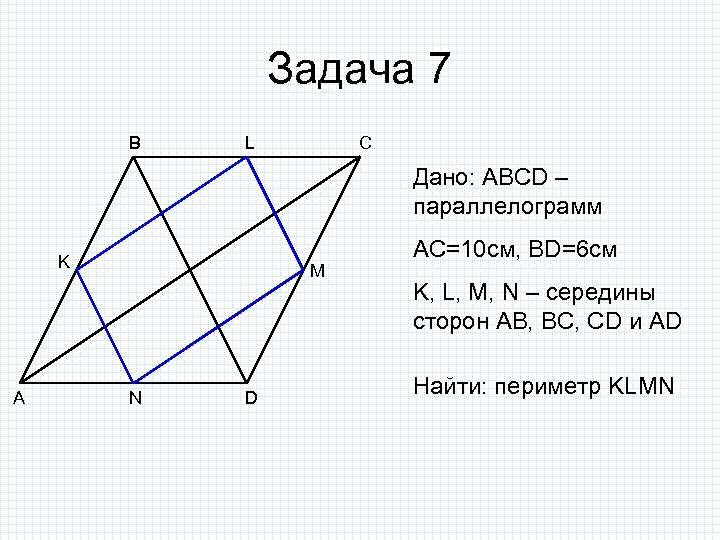Задача 7 B L C Дано: ABCD – параллелограмм K A M N D AC=10 см, BD=6 см K, L, M, N – середины сторон AB, BC, CD и AD Найти: периметр KLMN

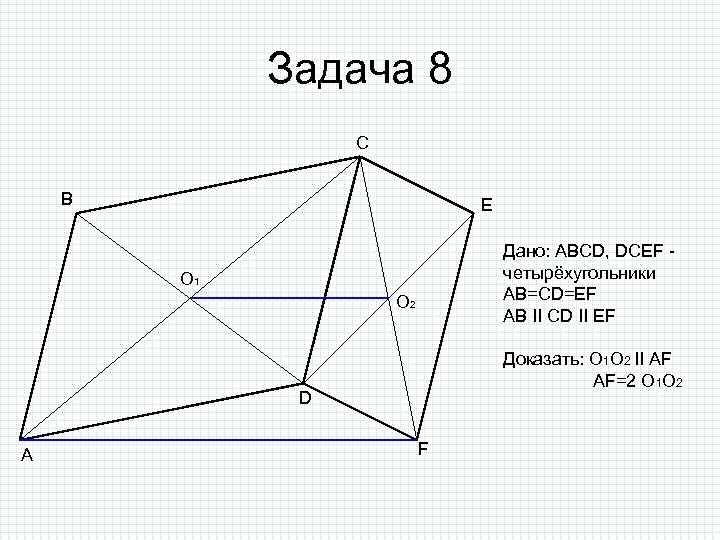Задача 8 C B E Дано: ABCD, DCEF четырёхугольники AB=CD=EF AB II CD II EF O 1 O 2 Доказать: O 1 O 2 II AF AF=2 O 1 O 2 D A F

Тест 1. Периметр треугольника, образованного средними линиями данного треугольника. , равен 14 см. Найти периметр данного треугольника А) 42 В) 7 С) 28 Д) 30 2. Стороны треугольника равны 6, 9, 13 м. Найдите стороны треугольника, образованного средними линиями данного треугольника. А) 2, 3, 3. 5 В) 18, 27, 39 С) 12, 18, 26 Д) 3, 4, 5, 6. 5 3. Периметр равностороннего треугольника равен 24 см. Найдите периметр треугольника, образованного средними линиями данного треугольника А) 48 В) 12 С) 6 Д) 18

Задание на дом П. 62, № 564, 566, 568.

ЖЕЛАЮ УДАЧИ!