Урок геометрии «Признаки подобия треугольников» 900 igr. net
Цель урока: Обобщение по теме «Признаки подобия треугольников» Задачи урока: 1. Обобщить и систематизировать теоретические знания ; 2. воспитание культуры личности, отношения к геометрии, как к части общечеловеческой культуры, играющей огромную роль в общественном развитии; 3. Повысить интерес к предмету.
Подобные фигуры В повседневной жизни встречаются предметы одинаковой формы, но разных размеров. В геометрии фигуры одинаковой формы называют подобными. Например:
Подобные треугольники A 1 A C B C 1 B Мы видим что соответственные углы не меняются т. е. A= A 1, B= B 1, C= C 1. Стороны изменились по длине. AB и A 1 B 1, BC и B 1 C 1, CA и C 1 A 1 называют сходственными. Два треугольника называются подобными, если их углы соответственно 1 равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Другими словами, два треугольника подобны, если можно обозначить буквами ABC и A 1 B 1 C 1 так, что A= A 1; B= B 1; C= C 1, AB: A 1 B 1=BC: B 1 C 1=CA: C 1 A 1=k. Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия.
ники оль еуг Тр бны? одо п В А С В 1 когда А 1 С 1
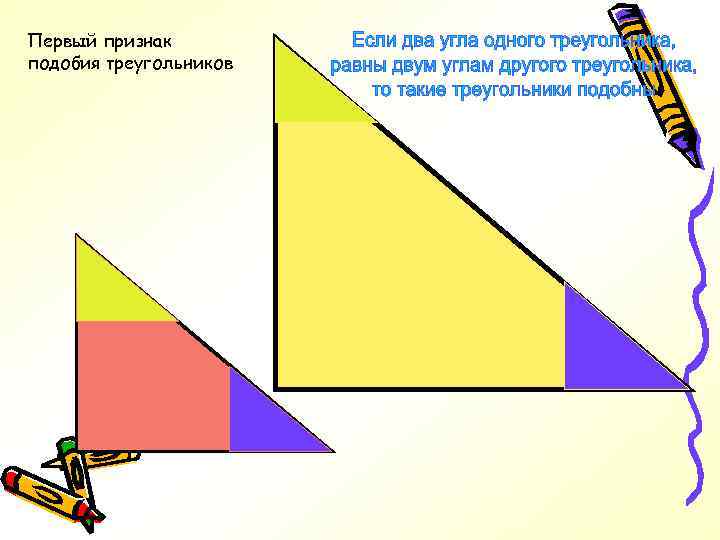
Первый признак подобия треугольников
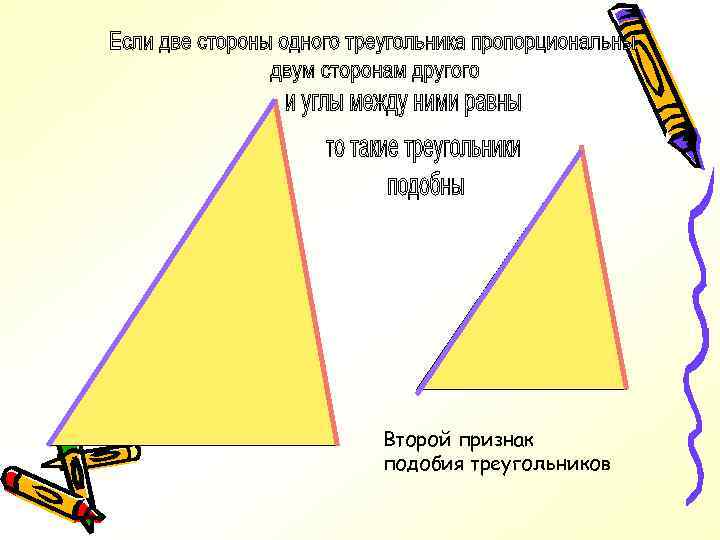
Второй признак подобия треугольников
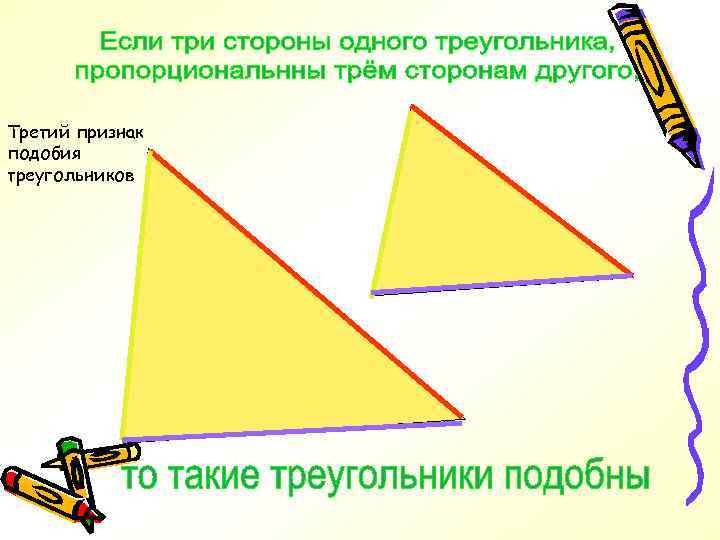
Третий признак подобия треугольников
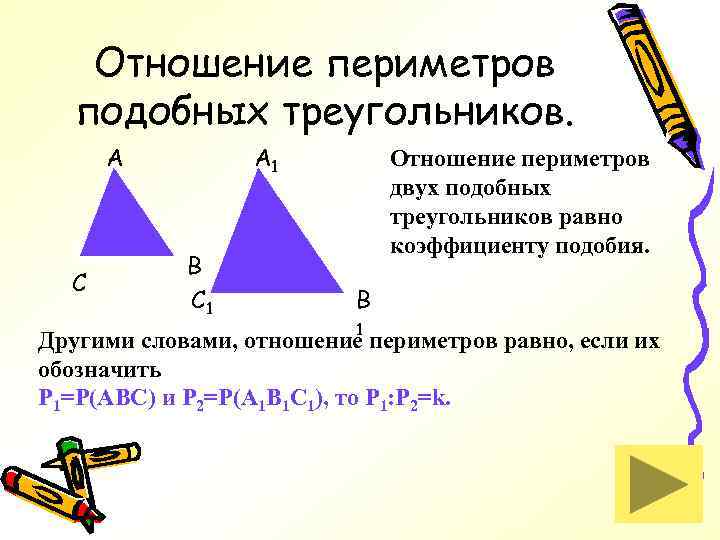
Отношение периметров подобных треугольников. A C A 1 B C 1 Отношение периметров двух подобных треугольников равно коэффициенту подобия. B 1 Другими словами, отношение периметров равно, если их обозначить P 1=P(ABC) и P 2=P(A 1 B 1 C 1), то P 1: P 2=k.
Отношение площадей подобных треугольников. S S 1 Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Другими словами, отношение площадей равно, если их площади обозначить S и S 1, то S: S 1=k 2. Конец
Используемая литература: Геометрия 7 -9/Л. С. Атанасян
Скачать презентацию Урок геометрии Признаки подобия треугольников 900 igr net
Признаки подобия треугольников.ppt