b567cae93462a169ae165ca9984fb646.ppt
- Количество слайдов: 26

Урок 54 -55 Подбор параметра

Решение алгебраических уравнений в Excel Дана функция 2 x - 4/x = y. Нам нужно, чтобы результат этой функции, т. е. y, был равен 7, выполним это командой Подбор параметра: В ячейку B 1, введём произвольное значение переменной x, например 1, а в B 3, функцию в виде формулы: • Вызываем окно Подбор параметра • В окне Подбор параметра вводим данные, и нажимаем ОК: значение в 3 -м поле команда подберёт такое, чтобы функция указанная в 1 -м параметре имела результат равный значению указанному во 2 -м параметре окна Подбор параметра. Результат работы команды:
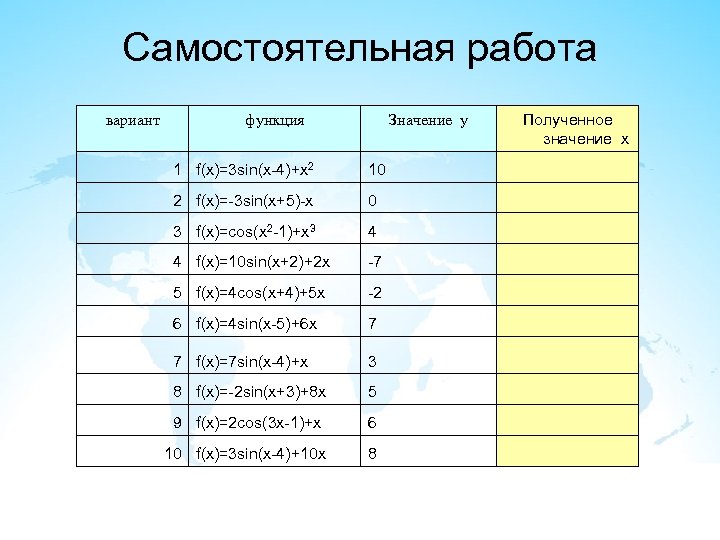
Самостоятельная работа вариант функция Значение у 1 f(x)=3 sin(x-4)+x 2 10 2 f(x)=-3 sin(x+5)-x 0 3 f(x)=cos(x 2 -1)+x 3 4 4 f(x)=10 sin(x+2)+2 x -7 5 f(x)=4 cos(x+4)+5 x -2 6 f(x)=4 sin(x-5)+6 x 7 7 f(x)=7 sin(x-4)+x 3 8 f(x)=-2 sin(x+3)+8 x 5 9 f(x)=2 cos(3 x-1)+x 6 10 f(x)=3 sin(x-4)+10 x 8 Полученное значение х

Решение экономических задач Нам нужно взять в банке кредит 10000 гривен под 20% на 1 год. Выплачивать мы хотим ежемесячно и одинаковую сумму. Рассчитывается он по разному, вот одна из формул: Арифметически формула записана в ячейке A 4:
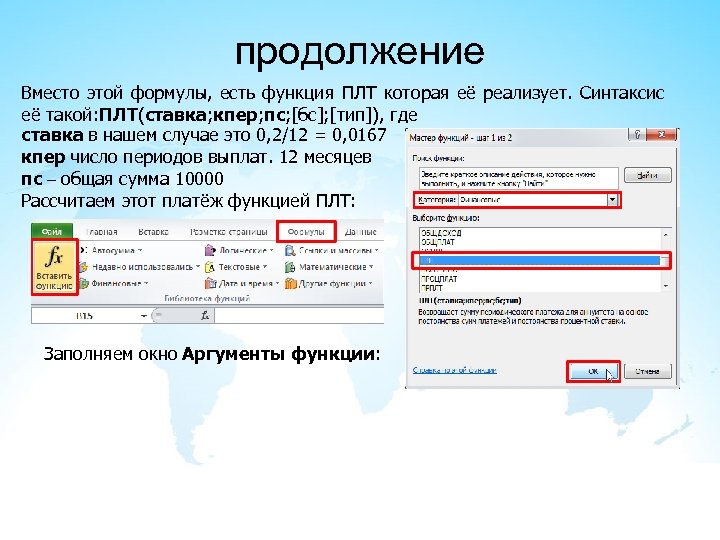
продолжение Вместо этой формулы, есть функция ПЛТ которая её реализует. Синтаксис её такой: ПЛТ(ставка; кпер; пс; [бс]; [тип]), где ставка в нашем случае это 0, 2/12 = 0, 0167 кпер число периодов выплат. 12 месяцев пс – общая сумма 10000 Рассчитаем этот платёж функцией ПЛТ: Заполняем окно Аргументы функции:
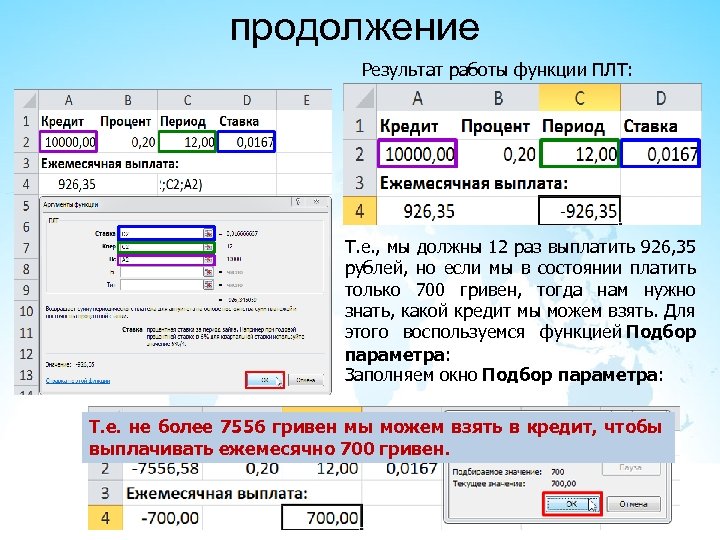
продолжение Результат работы функции ПЛТ: Т. е. , мы должны 12 раз выплатить 926, 35 рублей, но если мы в состоянии платить только 700 гривен, тогда нам нужно знать, какой кредит мы можем взять. Для этого воспользуемся функцией Подбор параметра: Заполняем окно Подбор параметра: Т. е. не более 7556 гривен мы можем взять в кредит, чтобы выплачивать ежемесячно 700 гривен.

Практическая работа 27 Тема Решение задач на подбор параметра Цель научиться решать задач на подбор параметра. Ход работы Выберите вариант задания по номеру компьютера. Решите задачу с помощью средства Подбор параметра. Подготовьте отчет по результатам в тетради.

Задания 1. 2. 3. 4. 5. Какую сумму кредита предстоит выплачивать клиенту ежемесячно, если взять в банке кредит 20000 гривен под 25% на 1 год? Как изменится сумма кредита, если клиент ежемесячно сможет выплачивать только _____ гривен? Какую сумму кредита предстоит выплачивать клиенту ежемесячно, если взять в банке кредит 15000 гривен под 22% на 2 года? Как изменится сумма кредита, если клиент ежемесячно сможет выплачивать только _____ гривен? Какую сумму кредита предстоит выплачивать клиенту ежемесячно, если взять в банке кредит 20000 гривен под 20% на 3 года? Как изменится сумма кредита, если клиент ежемесячно сможет выплачивать только _____ гривен? Какую сумму кредита предстоит выплачивать клиенту ежемесячно, если взять в банке кредит 50000 гривен под 26% на 2 года? Как изменится сумма кредита, если клиент ежемесячно сможет выплачивать только _____ гривен? Какую сумму кредита предстоит выплачивать клиенту ежемесячно, если взять в банке кредит 20000 гривен под 25% на 1 год? Как изменится сумма кредита, если клиент ежемесячно сможет выплачивать только _____ гривен?

Задания 6. Какую сумму кредита предстоит выплачивать клиенту ежемесячно, если взять в банке кредит 20000 гривен под 18% на 2 года? Как изменится сумма кредита, если клиент ежемесячно сможет выплачивать только _____ гривен? 7. Какую сумму кредита предстоит выплачивать клиенту ежемесячно, если взять в банке кредит 30000 гривен под 18% на 1 год? Как изменится сумма кредита, если клиент ежемесячно сможет выплачивать только _____ гривен? 8. Какую сумму кредита предстоит выплачивать клиенту ежемесячно, если взять в банке кредит 60000 гривен под 20% на 4 года? Как изменится сумма кредита, если клиент ежемесячно сможет выплачивать только _____ гривен? 9. Какую сумму кредита предстоит выплачивать клиенту ежемесячно, если взять в банке кредит 25000 гривен под 22% на 3 года? Как изменится сумма кредита, если клиент ежемесячно сможет выплачивать только _____ гривен? 10. Какую сумму кредита предстоит выплачивать клиенту ежемесячно, если взять в банке кредит 55000 гривен под 19% на 2 года? Как изменится сумма кредита, если клиент ежемесячно сможет выплачивать только _____ гривен?

Домашнее задание 1. Выучить конспект. 2. Решить задачу на подбор параметра с помощью математических расчётов (формулы) и с помощью средства Excel Подбор параметра. Какую сумму кредита предстоит выплачивать клиенту ежемесячно, если взять в банке кредит 50000 гривен под 20% на 2 года? Как изменится сумма кредита, если клиент ежемесячно сможет выплачивать только _____ гривен?

Оптимизационные задачи Урок 56

Что такое оптимизация? ОПТИМИЗАЦИЯ (от лат. Optimus-лучший) Под оптимизацией обычно понимают целенаправленную деятельность, которая заключается в получении наилучших результатов при соответствующих условиях. Постановка задачи оптимизации предполагает: • наличие ее объекта; • набора независимых параметров (переменных), описывающих данную задачу; • условий (ограничений), которые характеризуют приемлемые значения независимых переменных. • критерия оптимизации, (целевая функция), которая зависит от переменных оптимизации. Решение оптимизационной задачи - это поиск определенного набора значений переменных, которому соответствует оптимальное значение критерия оптимизации.

Примеры оптимизационных задач (ОЗ) • Штатное расписание, т. е. вы можете составить штатное расписание, для достижения наилучших результатов, при соответствии наименьших затратах. • Планирование перевозок, так называемая Транспортная задача. • Составление смесей, и так далее. Задачи, лучше решаются с помощью этого средства и имеют два свойства, во-первых, у них цель максимизировать или минимизировать что-то, т. е. максимизировать прибыль, либо минимизировать расходы, во-вторых, есть ограничения, которые обычно выражаются в виде неравенств.

Основные понятия Переменные - неизвестные величины, значения которых нужно найти в результате решения задачи. Целевая функция - величина, которая зависит от переменных и значение которой нужно максимизировать или минимизировать. Критерий - требование минимизации или максимизации целевой функции. Ограничения - условия, которым должны удовлетворять переменные.

Алгоритм решения ОЗ: 1. Введение обозначений. (что и как будем обозначать) 2. Создание целевой функции и критерия (что будем максимизировать или минимизировать и записать формулу зависимости этой величины от переменных) 3. Составление системы ограничений. (Неравенства или равенства) 4. Решение задачи средствами Excel.
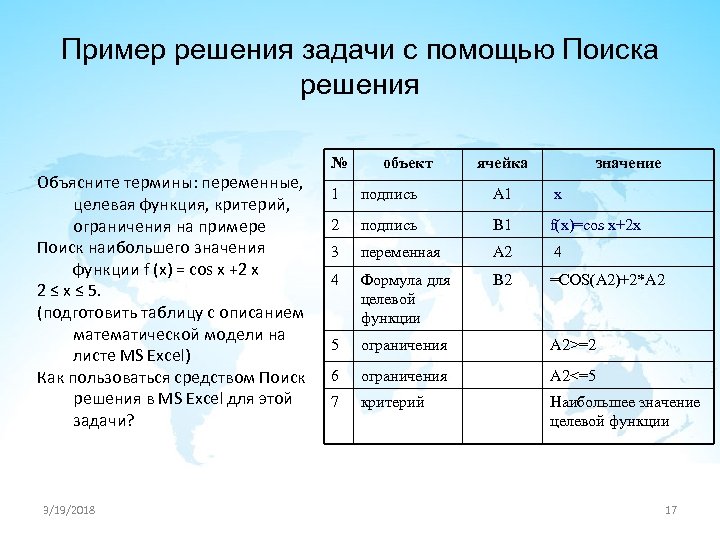
Пример решения задачи с помощью Поиска решения Объясните термины: переменные, целевая функция, критерий, ограничения на примере Поиск наибольшего значения функции f (x) = cos x +2 x 2 ≤ x ≤ 5. (подготовить таблицу с описанием математической модели на листе MS Excel) Как пользоваться средством Поиск решения в MS Excel для этой задачи? 3/19/2018 № объект ячейка значение 1 подпись А 1 х 2 подпись В 1 f(x)=cos x+2 x 3 переменная А 2 4 4 Формула для целевой функции В 2 =COS(A 2)+2*A 2 5 ограничения А 2>=2 6 ограничения A 2<=5 7 критерий Наибольшее значение целевой функции 17

Поиск решения в MS Excel 3/19/2018 18

Отчет по результатам 3/19/2018 19
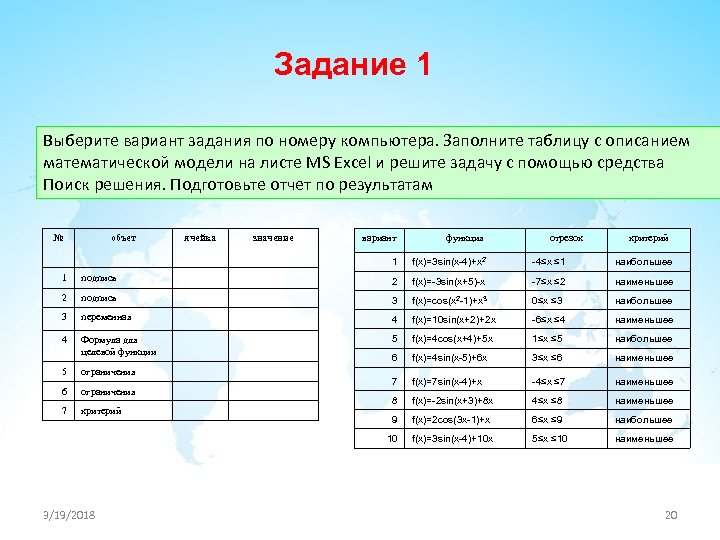
Задание 1 Выберите вариант задания по номеру компьютера. Заполните таблицу с описанием математической модели на листе MS Excel и решите задачу с помощью средства Поиск решения. Подготовьте отчет по результатам № объет ячейка значение вариант функция отрезок критерий 1 f(x)=3 sin(x-4)+x 2 -4≤x ≤ 1 наибольшее 1 подпись 2 f(x)=-3 sin(x+5)-x -7≤x ≤ 2 наименьшее 2 подпись 3 f(x)=cos(x 2 -1)+x 3 0≤x ≤ 3 наибольшее 3 переменная 4 f(x)=10 sin(x+2)+2 x -6≤x ≤ 4 наименьшее 4 Формула для целевой функции 5 f(x)=4 cos(x+4)+5 x 1≤x ≤ 5 наибольшее 6 f(x)=4 sin(x-5)+6 x 3≤x ≤ 6 наименьшее 5 ограничения 6 ограничения 7 f(x)=7 sin(x-4)+x -4≤x ≤ 7 наименьшее 7 критерий 8 f(x)=-2 sin(x+3)+8 x 4≤x ≤ 8 наименьшее 9 f(x)=2 cos(3 x-1)+x 6≤x ≤ 9 наибольшее 10 f(x)=3 sin(x-4)+10 x 5≤x ≤ 10 наименьшее 3/19/2018 20

Задание 2. Старинная русская задача Пошла баба на базар на людей посмотреть и что-то продать. Сколько нужно бабе на базар для продажи живых гусей, уток и кур, чтобы выручить побольше денег, если она может взять товара массой не более Р килограмм? Причем известно, что: Масса одной курицы - В 2, стоимость - С 2 Масса одной утки - В 3, стоимость - С 3 Масса одного гуся - В 4, стоимость - С 4

Математическая модель задачи масса одной курицы - В 2, стоимость - С 2 масса одной утки - В 3, стоимость - С 3 масса одного гуся - В 4, стоимость - С 4 D 2, D 3, D 4 - число кур, уток и гусей соответственно, взятых бабой для продажи. Задача бабы - выручить побольше денег - описывается целевой функцией: С 2 * D 2 + C 3 * D 3 + C 4 * D 4 → max. Так как баба может взять не более Р кг товара, то должно выполняться условие: В 2 * D 2 + В 3 * D 3 + В 4 * D 4 ≤ Р Кроме того, имеют место ограничения: D 2 ≥ 0, D 3 ≥ 0, D 4 ≥ 0, D 2, D 3, D 4 - целые.
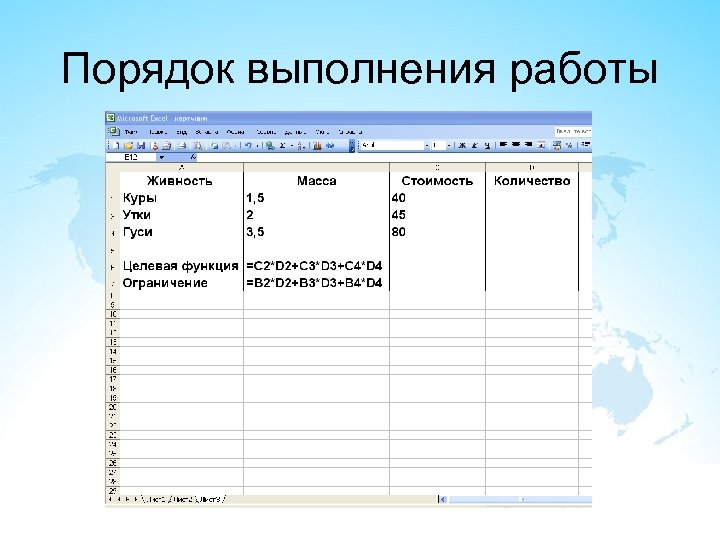
Порядок выполнения работы
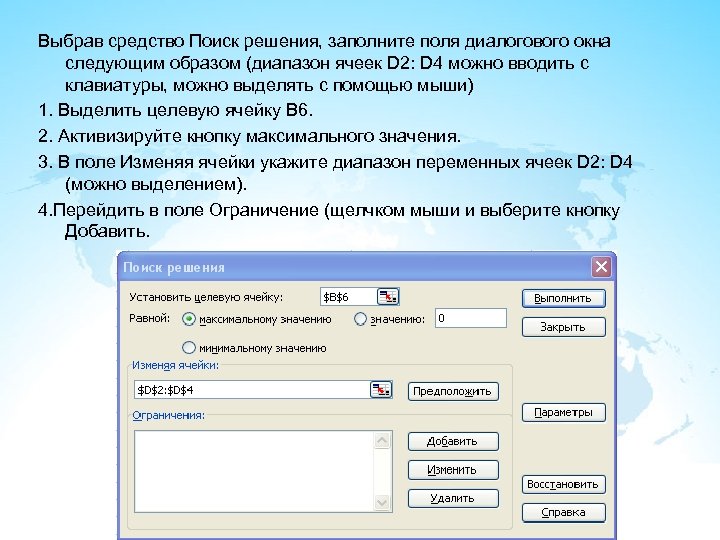
Выбрав средство Поиск решения, заполните поля диалогового окна следующим образом (диапазон ячеек D 2: D 4 можно вводить с клавиатуры, можно выделять с помощью мыши) 1. Выделить целевую ячейку В 6. 2. Активизируйте кнопку максимального значения. 3. В поле Изменяя ячейки укажите диапазон переменных ячеек D 2: D 4 (можно выделением). 4. Перейдить в поле Ограничение (щелчком мыши и выберите кнопку Добавить.
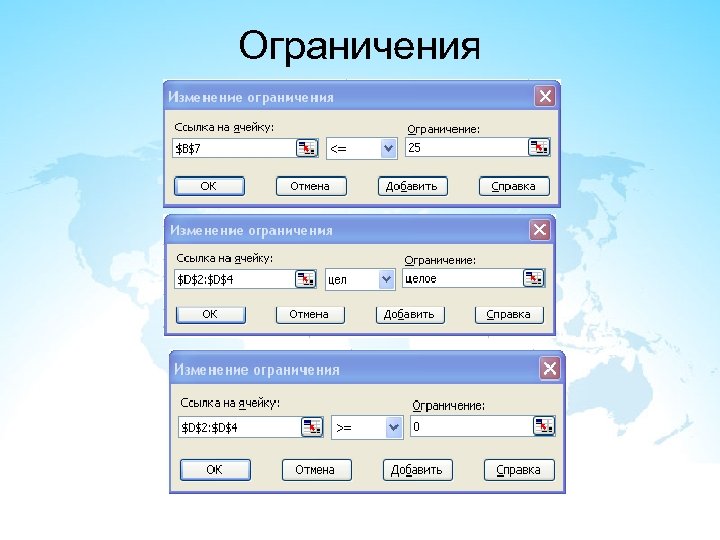
Ограничения
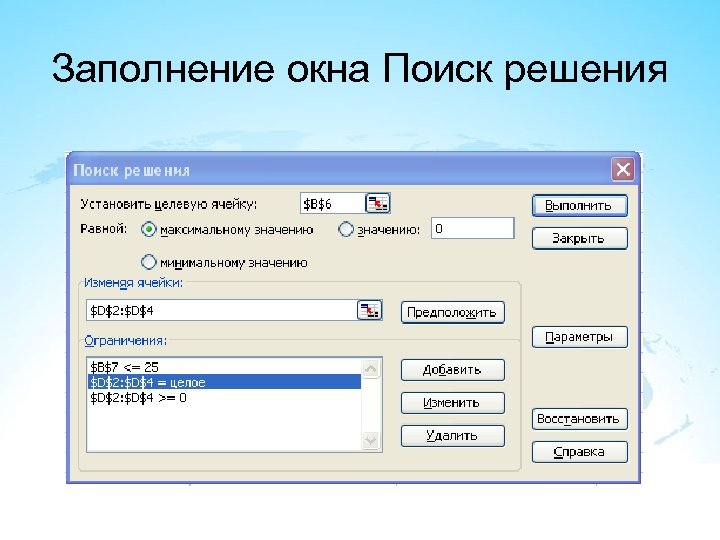
Заполнение окна Поиск решения

Домашнее задание Выучить конспект.
b567cae93462a169ae165ca9984fb646.ppt