 Урок № 4 ПОВТОРЕНИЕ Выражения с логарифмами log – знак логарифма, a – основание логарифма, b – выражение под логарифмом И не пытайся понять мою душу: там такие, сударь ты мой, логарифмы! Авессалом Подводный. Отдельные мысли
Урок № 4 ПОВТОРЕНИЕ Выражения с логарифмами log – знак логарифма, a – основание логарифма, b – выражение под логарифмом И не пытайся понять мою душу: там такие, сударь ты мой, логарифмы! Авессалом Подводный. Отдельные мысли
 ОПРЕДЕЛЕНИЕ Теория ОСНОВНОЕ ЛОГАРИФМИЧЕСКОЕ ТОЖДЕСТВО ДЕСЯТИЧНЫЕ И НАТУРАЛЬНЫЕ ЛОГАРИФМЫ СВОЙСТВА ЛОГАРИФМОВ
ОПРЕДЕЛЕНИЕ Теория ОСНОВНОЕ ЛОГАРИФМИЧЕСКОЕ ТОЖДЕСТВО ДЕСЯТИЧНЫЕ И НАТУРАЛЬНЫЕ ЛОГАРИФМЫ СВОЙСТВА ЛОГАРИФМОВ
 =х Устно Логарифмом положительного числа b по основанию a, где называется показатель степени в которую нужно возвести a, чтобы получить b.
=х Устно Логарифмом положительного числа b по основанию a, где называется показатель степени в которую нужно возвести a, чтобы получить b.
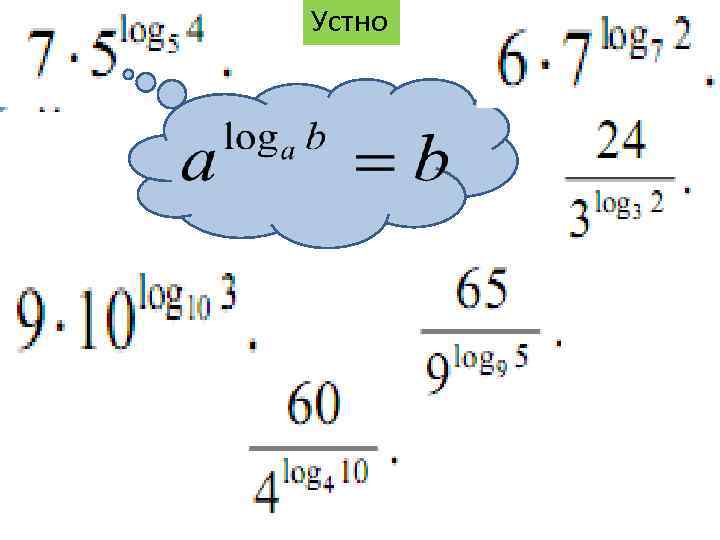 Устно
Устно
 Устно логарифм единицы равен нулю логарифм a по основанию a равен единице
Устно логарифм единицы равен нулю логарифм a по основанию a равен единице
 Устно логарифм произведения положительных множителей равен сумме логарифмов этих множителей логарифм частного положительных числителя и знаменателя равен разности логарифма числителя и логарифма знаменателя
Устно логарифм произведения положительных множителей равен сумме логарифмов этих множителей логарифм частного положительных числителя и знаменателя равен разности логарифма числителя и логарифма знаменателя
 Устно Вычислите
Устно Вычислите
 Предложите, как лучше запомнить данные две формулы? логарифм степени равен произведению показателя степени на логарифм основания Устно
Предложите, как лучше запомнить данные две формулы? логарифм степени равен произведению показателя степени на логарифм основания Устно
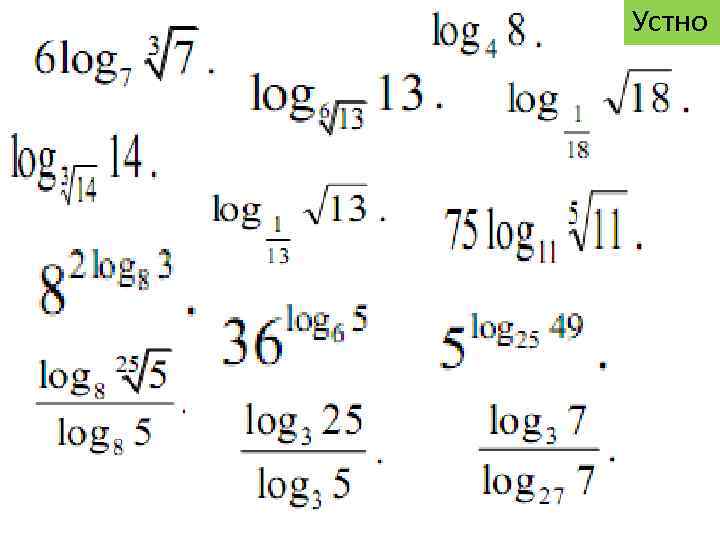 Устно
Устно
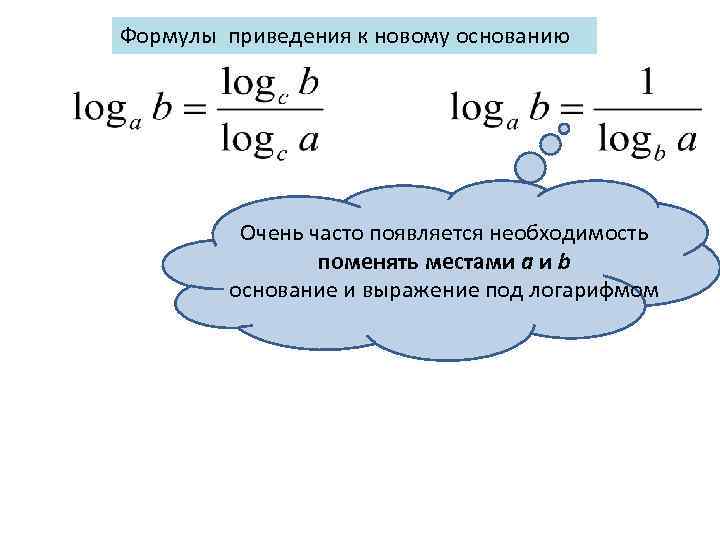 Формулы приведения к новому основанию Очень часто появляется необходимость поменять местами a и b основание и выражение под логарифмом
Формулы приведения к новому основанию Очень часто появляется необходимость поменять местами a и b основание и выражение под логарифмом
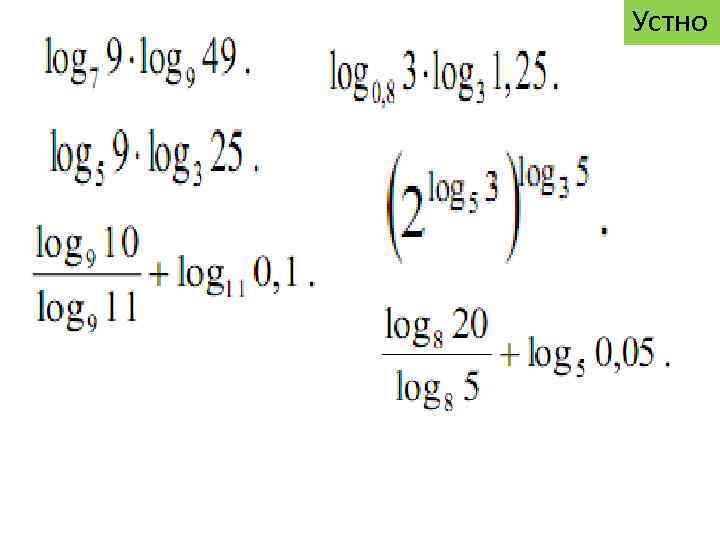 Устно
Устно
 Письменно В классе нечётные номера, дома – чётные. 1 6 2 7 3 4 5 8 9
Письменно В классе нечётные номера, дома – чётные. 1 6 2 7 3 4 5 8 9
 Письменно 10 16 11 17 12 13 14 15 18 19
Письменно 10 16 11 17 12 13 14 15 18 19
 Письменно 20 21 Дополнительная задачка Домашнее задание № 4 В классе нечётные номера, дома – чётные.
Письменно 20 21 Дополнительная задачка Домашнее задание № 4 В классе нечётные номера, дома – чётные.
 Дробь равна нулю, если числитель равен нулю, а знаменатель нулю не равен. Уравнение будет иметь ровно один корень, если 1) дискриминант квадратного уравнения равен нулю и корни не совпадают с числами 3 и -3; 2) дискриминант положителен и один из корней равен 3 или -3. { 1) D=(3 -a)²+4(2 a²-3 a)=0 -9+3(3 -a)+2 a²-3 a≠ 0 -9 -3(3 -a)+2 a²-3 a≠ 0 { 2) D=(3 -a)²+4(2 a²-3 a)>0 -9+3(3 -a)+2 a²-3 a=0 -9 -3(3 -a)+2 a²-3 a=0
Дробь равна нулю, если числитель равен нулю, а знаменатель нулю не равен. Уравнение будет иметь ровно один корень, если 1) дискриминант квадратного уравнения равен нулю и корни не совпадают с числами 3 и -3; 2) дискриминант положителен и один из корней равен 3 или -3. { 1) D=(3 -a)²+4(2 a²-3 a)=0 -9+3(3 -a)+2 a²-3 a≠ 0 -9 -3(3 -a)+2 a²-3 a≠ 0 { 2) D=(3 -a)²+4(2 a²-3 a)>0 -9+3(3 -a)+2 a²-3 a=0 -9 -3(3 -a)+2 a²-3 a=0
 1 { D=(3 -a)²+4(2 a²-3 a)=0 -9+3(3 -a)+2 a²-3 a≠ 0 -9 -3(3 -a)+2 a²-3 a≠ 0 2 { D=(3 -a)²+4(2 a²-3 a)>0 -9+3(3 -a)+2 a²-3 a=0 -9 -3(3 -a)+2 a²-3 a=0 1 D=(3 -a)²+4(2 a²-3 a)=0 -9+3(3 -a)+2 a²-3 a≠ 0 -9 -3(3 -a)+2 a²-3 a≠ 0 9 -6 a+a²+8 a²-12 a=0 2 a²-6 a≠ 0 2 a²≠ 18 9 a²-18 a+9=0 |: 9 a≠ 0 a≠ 3 a≠-3 a≠ 3 a²-2 a+1=0 (a-1)²=0 При a=1 уравнение имеет ровно одно решение. a=1 2 D=(3 -a)²+4(2 a²-3 a)>0 -9+3(3 -a)+2 a²-3 a=0 -9 -3(3 -a)+2 a²-3 a=0 (a-1)²>0 a=3 a=-3 a=3 a≠ 1 При a=0 и a=-3 уравнение имеет ровно одно решение. Ответ: при a=0, a=1, a=3 исходное уравнение имеет ровно одно решение.
1 { D=(3 -a)²+4(2 a²-3 a)=0 -9+3(3 -a)+2 a²-3 a≠ 0 -9 -3(3 -a)+2 a²-3 a≠ 0 2 { D=(3 -a)²+4(2 a²-3 a)>0 -9+3(3 -a)+2 a²-3 a=0 -9 -3(3 -a)+2 a²-3 a=0 1 D=(3 -a)²+4(2 a²-3 a)=0 -9+3(3 -a)+2 a²-3 a≠ 0 -9 -3(3 -a)+2 a²-3 a≠ 0 9 -6 a+a²+8 a²-12 a=0 2 a²-6 a≠ 0 2 a²≠ 18 9 a²-18 a+9=0 |: 9 a≠ 0 a≠ 3 a≠-3 a≠ 3 a²-2 a+1=0 (a-1)²=0 При a=1 уравнение имеет ровно одно решение. a=1 2 D=(3 -a)²+4(2 a²-3 a)>0 -9+3(3 -a)+2 a²-3 a=0 -9 -3(3 -a)+2 a²-3 a=0 (a-1)²>0 a=3 a=-3 a=3 a≠ 1 При a=0 и a=-3 уравнение имеет ровно одно решение. Ответ: при a=0, a=1, a=3 исходное уравнение имеет ровно одно решение.