Урок 3 МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ Декартовы

Урок № 3 МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ Декартовы координаты в пространстве Рене Дека рт, французский философ, математик, механик, физик и физиолог Высь, ширь, глубь. Лишь три координаты. Мимо них где путь? Засов закрыт. С Пифагором слушай сфер сонаты, Атомам дли счёт, как Демокрит. В. Брюсов.

План урока 1 Введение прямоугольной системы координат в пространстве. 2 Расположение точек в системе координат. 3 Нахождение координат точек в пространстве. 4 Построение точки в пространстве по её координатам. 5 Понятие радиус-вектора. 6 Разложение вектора по координатным векторам. 7 Нахождение координат вектора суммы векторов, вектора разности векторов, вектора умноженного на данное число. 8 Решение задач. 9 Запись ДЗ.

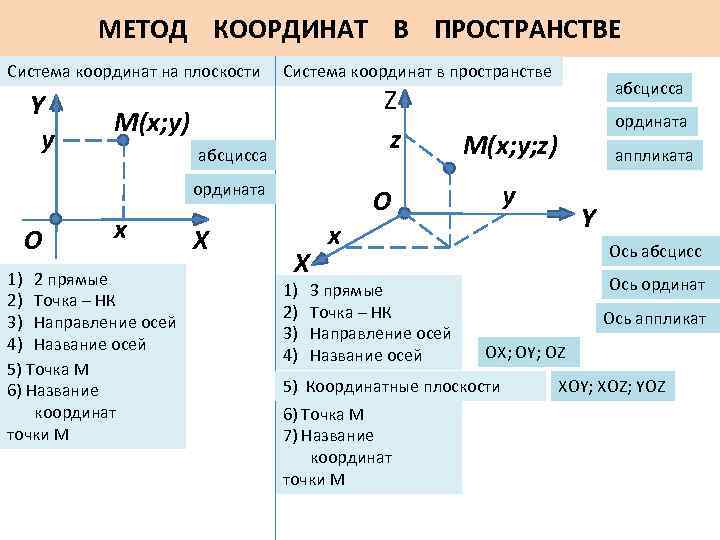МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ Система координат на плоскости Y y Система координат в пространстве Z z M(x; y) абсцисса ордината О x 1) 2 прямые 2) Точка – НК 3) Направление осей 4) Название осей 5) Точка М 6) Название координат точки М X X 1) 2) 3) 4) x аппликата y Y Ось абсцисс Ось ординат Ось аппликат OX; OY; OZ 5) Координатные плоскости 6) Точка М 7) Название координат точки М ордината M(x; y; z) О 3 прямые Точка – НК Направление осей Название осей абсцисса XOY; XOZ; YOZ

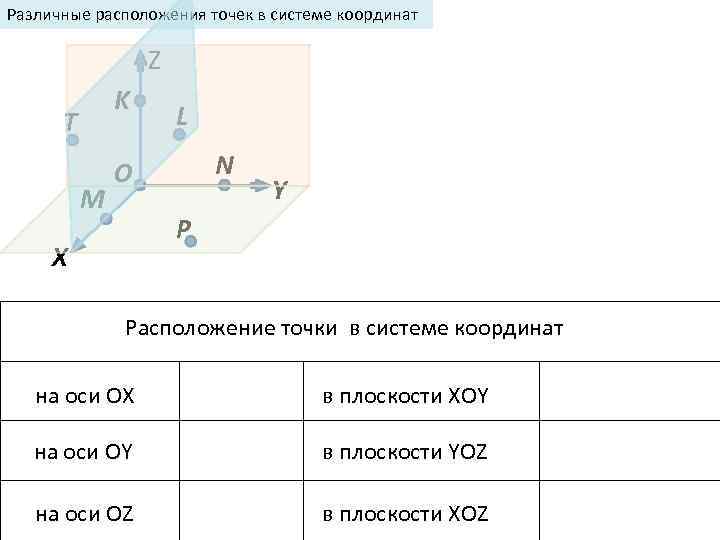Различные расположения точек в системе координат Z K T M L N О Y P X Расположение точки в системе координат на оси ОХ в плоскости ХOY на оси ОY в плоскости YOZ на оси ОZ в плоскости ХOZ

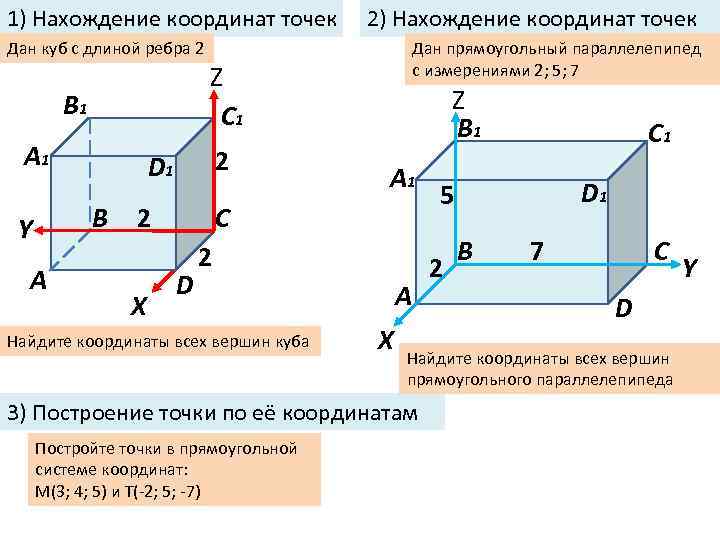1) Нахождение координат точек 2) Нахождение координат точек Дан куб с длиной ребра 2 Z C 1 B 1 A 2 D 1 B Y Дан прямоугольный параллелепипед с измерениями 2; 5; 7 2 X Z B 1 A 1 C D 2 Найдите координаты всех вершин куба A X D 1 5 2 B 7 C D Найдите координаты всех вершин прямоугольного параллелепипеда 3) Построение точки по её координатам Постройте точки в прямоугольной системе координат: М(3; 4; 5) и Т(-2; 5; -7) C 1 Y

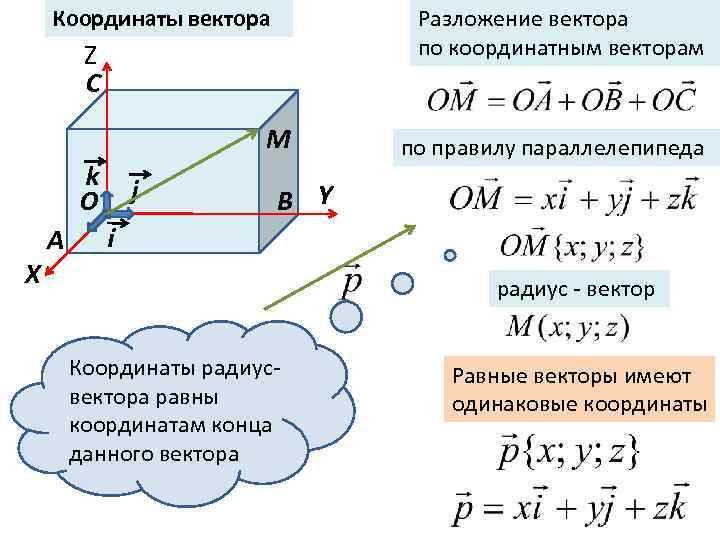Координаты вектора Разложение вектора по координатным векторам Z С М k О X А j по правилу параллелепипеда В Y i радиус - вектор Координаты радиусвектора равны координатам конца данного вектора Равные векторы имеют одинаковые координаты

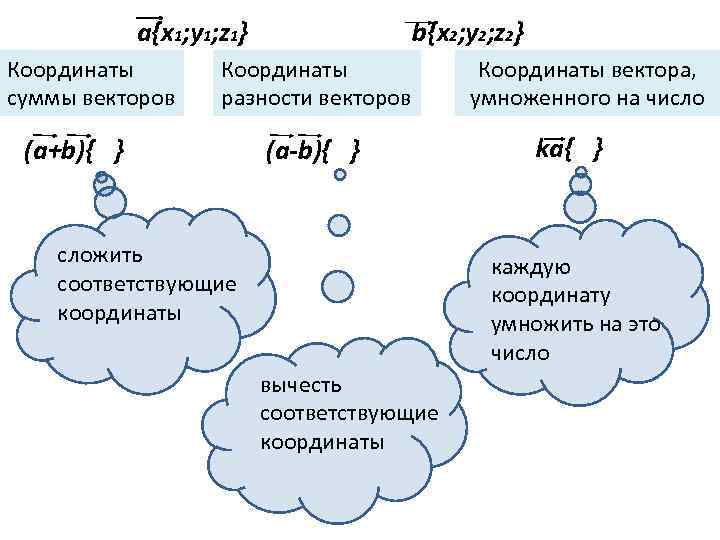a{x 1; y 1; z 1} Координаты суммы векторов b{x 2; y 2; z 2} Координаты разности векторов (a+b){ } (a-b){ } сложить соответствующие координаты Координаты вектора, умноженного на число ka{ } каждую координату умножить на это число вычесть соответствующие координаты

4) Дано разложение вектора по единичным векторам, запишите координаты вектора. 5) Даны координаты вектора, запишите разложение вектора по единичным векторам.

Домашнее задание с урока 3: п. 46, 47 и конспект, уметь составить грамотный рассказ, № 400, 402, 403, 404, 410 на следующем уроке простейшая СР