Урок 20 1 зад а Намерете

Урок № 20

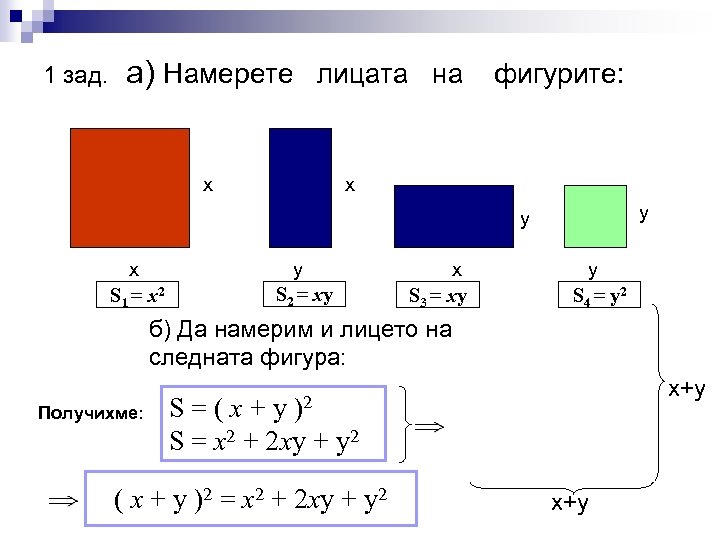1 зад. а) Намерете лицата на фигурите: x x y y x S 1 = x 2 y S 2 = xy x S 3 = xy y S 4 = y 2 б) Да намерим и лицето на следната фигура: Получихме: x+y )2 S=(x+y S = x 2 + 2 xy + y 2 ( x + y )2 = x 2 + 2 xy + y 2 x+y

2 зад. Да пресметнем по познатият ни начин (х + у)2 , Разлагаме на множители: (х + у)2 = (х + у) = = х2 + х. у + у2 = = х2 + 2 ху + у2 Отново получихме : (х + у)2 = х2 + 2 ху + у2

ІІІ раздел ФОРМУЛИ ЗА СЪКРАТЕНО УМНОЖЕНИЕ Формулите (u ± v)2 = u 2 ± 2 uv + v 2 1. Представяне на сбор на квадрат с нормален многочлен.

И в двата примера ние получихме един и същ резултат : първо второ (х + у)2 = х2 + 2 х у + у2 първото на квадрат два пъти първото по второто на квадрат Можем да запишем формулата: (u + v)2 = u 2 + 2 uv + v 2 Квадратът на сбор от два израза u и v е равен на квадрата на първия израз плюс удвоеното произведение на първия и втория, плюс квадрата на втория израз.

Да приложим формулата : (u + v)2 = u 2 + 2 uv + v 2 ( u + v )2 = u 2 + 2 u v + v 2 1. 2. ( a + b )2 = 3 x 5 ( + )2 = a 4 2

Да приложим формулата : (u + v)2 = u 2 + 2 uv + v 2 ( a + b )2 = u 2 + 2 u v + v 2 1. 2. ( a + b )2 = 3 x 5 ( + )2 = a 4 2 a 2 + 2 a b + b 2

Да приложим формулата : (u + v)2 = u 2 + 2 uv + v 2 ( u + v )2 = 1. 2. ( a + b )2 = 3 x 5 ( + )2 = a 4 2 u 2 + 2 u v + v 2 a 2 + 2 a b + b 2

Да приложим формулата : (u + v)2 = u 2 + 2 uv + v 2 ( 3 x + 5 )2 = ( u)2 + 2. u. v + v 2 1. 2. ( a + b )2 = a 2 + 2 a b + b 2 3 x 5 ( + )2 = 9 x 2 + 30 x + 25 a 2 + 8 a + 16 a 4 2

2. Представяне на разлика на квадрат с нормален многочлен. Знаем формулата (u + v)2 = u 2 + 2 uv + v 2 Да пресметнем : (u – v)2 =[u + (-v)]2 = = u 2 + 2. u. (-v) + (-v)2 = = u 2 – 2 uv + v 2 Или получихме формулата: (u – v)2 = u 2 – 2 uv + v 2

Да използваме формулата (u – v)2 = u 2 – 2 uv + v 2 в няколко примера: 3)2 1. 2. 3. (a – = a 2 – 2. a. 3 + 32 = = a 2 – 6 a + 9 (5 – 3 x)2 = 52 – 2. 5. 3 x + (3 x)2 = = 25 – 30 x + 9 x 2 = = 9 x 2 – 30 x + 25 (4 x – 7 y 2)2 = (4 x)2 – 2. 4 x. 7 y 2 + (7 y 2)2 = = 16 x 2 – 56 xy 2 + 49 y 4

Двете формули се записват за по–кратко : (u ± 2 v) = 2 u ± 2 uv + 2 v и са известни като формули за сбор и разлика на квадрат n А от свойствата на степените получаваме тъждествата : n (х + у)2 = (– x – y)2 ; n n (aх + aу)2 = a 2( x + y)2 n (aх – aу)2 = a 2( x – y)2 (х – у)2 = (y – x)2 ;

(u ± v)2 = u 2 ± 2 uv + v 2 3. Приложение. 1) Да се представи с нормален многочлен изразът: (2 x – 1)2 – ( x – 3)(2 + x ) – 5 x = = (2 x)2 – 2. 2 x. 1 + 12– (2 x + x 2– 6 – 3 x) – 5 x = = 4 x 2 – 4 x + 1 – 2 x – x 2 + 6 + 3 x – 5 x = = 3 x 2 – 8 x + 7

(u ± v)2 = u 2 ± 2 uv + v 2 Стр. 58 / 6 а) Решете уравнението: (x – 3)2 – x 2 = 5 x 2 – 2. x. 3 + 32 – x 2 = 5 – 6 x + 9 = 5 – 6 x = 5 – 9 – 6 x = – 4 / : (– 6) x=

(u ± v)2 = u 2 ± 2 uv + v 2 2) Да се пресметне 992 = (100 – 1)2 = = 1002 – 2. 100. 1 + 12 = = 10 000 – 200 +1 = = 9 801

(u ± v)2 = u 2 ± 2 uv + v 2 3) Да пресметнем: (x + y + z)2 = = [(x + y) + z]2 = = (x + y)2 + 2(x + y)z + z 2 = = x 2 + 2 xy + y 2 + 2 xz + 2 yz + z 2 = = x 2 + y 2 + z 2 + 2 xy + 2 xz + 2 yz Получихме : (x + y + z)2 = x 2 + y 2 + z 2 + 2 xy + 2 xz + 2 yz

(u ± v)2 = u 2 ± 2 uv + v 2 стр. 58/ 1 a) 1. а) (x + 5)2 = x 2 +2. x. 5 + 52 = = x 2 +10 x + 25 = 42 + 2. 4. x + x 2 = (4 + x)2 = x 2 + 8 x + 16 = x 2 – 2. x. 5 +52 = (x – 5)2 = x 2 – 10 x +25 = x 2 – 8 x + 16 (4 – x)2

1) (х + у)2 = (– x – y)2 2) (х – у)2 = (y – x)2 стр. 58/ 2. а)б) (u ± v)2 = u 2 ± 2 uv + v 2 3) (aх + aу)2 = a 2( x + y)2 4) (aх – aу)2 = a 2( x – y)2 – първите два примера от всеки ред 2. а) (–x +4)2 = (4 – x )2 = 16 – 8 x + x 2 = = x 2 – 8 x + 16 (–y – 3)2 = (y + 3)2 = = y 2 + 6 y + 9 б) (3 x – 3 y)2 = 32. (x – y)2 = = 9(х2 – 2 ху + у2)= = 9 х2 – 18 ху + 9 у2 (– 2 x– 2 y)2 = (– 2)2. (x + y)2= = 4(х2 + 2 ху + у2) = = 4 х2 + 8 ху + 4 у2

(u ± v)2 = u 2 ± 2 uv + v 2 стр. 58/5 а)б) – първите два примера 5. а) 2 (5 x + 1)2 – = 25 x 2 + 10 x + 1 – 2 = = 25 x 2 + 10 x – 1 = – 48 + x 2 – 14 x + 49 = – 48 + (x – 7)2= x 2 – 14 x + 1 = x 2 – 12 x + 36 – x 2 + 12 x = б) (x – 6)2 – x(x – 12) = 36 = 4 x 2 +20 x +25 + 4 x 2 – 20 x +25= (2 x + 5)2 + (2 x – 5)2 = 8 x 2 + 50

Стр. 58 / 6 а) (2 y + 1)2 – 4 y 2 = 7 (2 y)2 + 2. 2 y. 1 + 12 – 4 y 2 = 7 4 y 2 + 4 y + 1 – 4 y 2 = 7 4 y + 1 = 7 4 y = 7 – 1 4 y = 6 /: 4 y = 1, 5

Да обобщим: Формулите за сбор и разлика на квадрат са : (u ± 2 v) = 2 u ± 2 uv + 2 v

За домашна работа: стр. 58 / 1 б), 5 в), 6 в) ДОВИЖДАНЕ!