 Урок № 1 Векторы на плоскости и в пространстве «В огромном саду геометрии каждый найдет букет себе по вкусу» Давид Гильберт Ве ктор (от лат. vector, «несущий» ) — в простейшем случае математический объект, характеризующийся величиной и направлением.
Урок № 1 Векторы на плоскости и в пространстве «В огромном саду геометрии каждый найдет букет себе по вкусу» Давид Гильберт Ве ктор (от лат. vector, «несущий» ) — в простейшем случае математический объект, характеризующийся величиной и направлением.
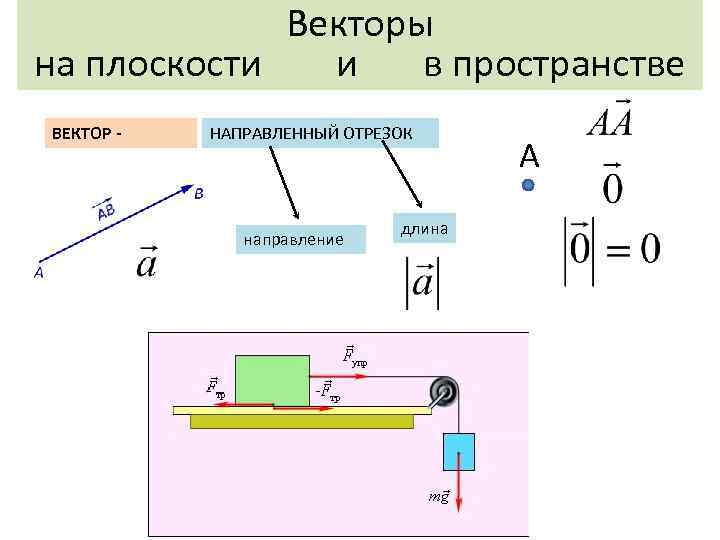 Векторы на плоскости и в пространстве ВЕКТОР - НАПРАВЛЕННЫЙ ОТРЕЗОК направление длина А
Векторы на плоскости и в пространстве ВЕКТОР - НАПРАВЛЕННЫЙ ОТРЕЗОК направление длина А
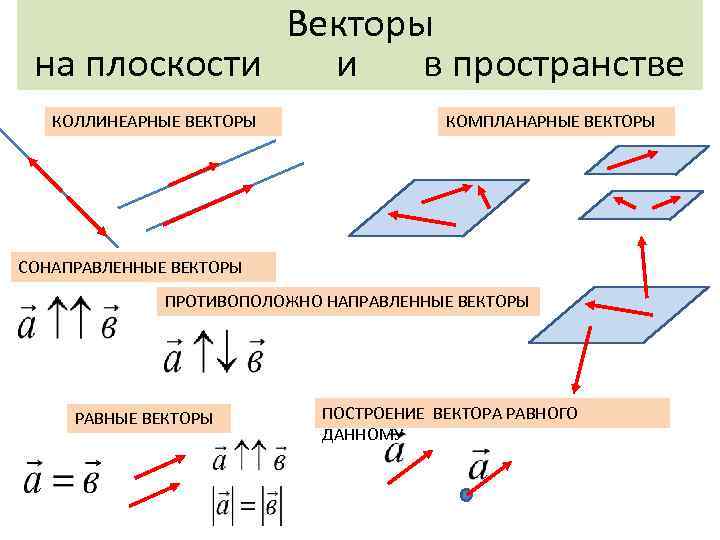 Векторы на плоскости и в пространстве КОЛЛИНЕАРНЫЕ ВЕКТОРЫ КОМПЛАНАРНЫЕ ВЕКТОРЫ СОНАПРАВЛЕННЫЕ ВЕКТОРЫ ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫЕ ВЕКТОРЫ РАВНЫЕ ВЕКТОРЫ ПОСТРОЕНИЕ ВЕКТОРА РАВНОГО ДАННОМУ
Векторы на плоскости и в пространстве КОЛЛИНЕАРНЫЕ ВЕКТОРЫ КОМПЛАНАРНЫЕ ВЕКТОРЫ СОНАПРАВЛЕННЫЕ ВЕКТОРЫ ПРОТИВОПОЛОЖНО НАПРАВЛЕННЫЕ ВЕКТОРЫ РАВНЫЕ ВЕКТОРЫ ПОСТРОЕНИЕ ВЕКТОРА РАВНОГО ДАННОМУ
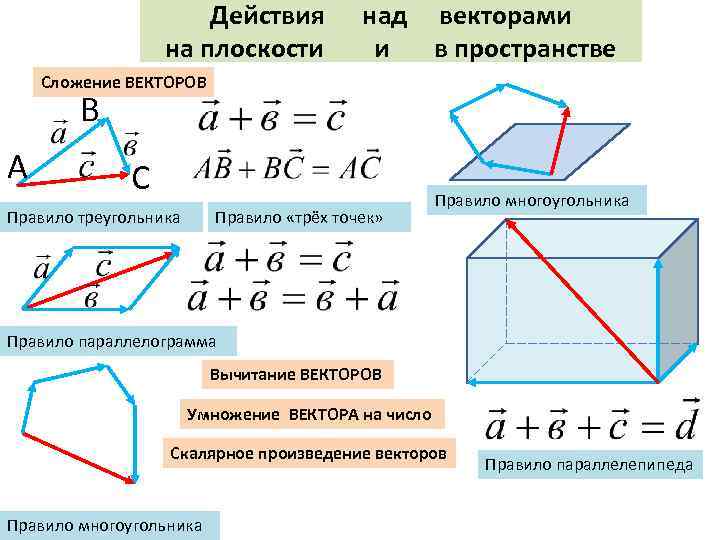 Действия над векторами на плоскости и в пространстве Сложение ВЕКТОРОВ В А С Правило треугольника Правило «трёх точек» Правило многоугольника Правило параллелограмма Вычитание ВЕКТОРОВ Умножение ВЕКТОРА на число Скалярное произведение векторов Правило многоугольника Правило параллелепипеда
Действия над векторами на плоскости и в пространстве Сложение ВЕКТОРОВ В А С Правило треугольника Правило «трёх точек» Правило многоугольника Правило параллелограмма Вычитание ВЕКТОРОВ Умножение ВЕКТОРА на число Скалярное произведение векторов Правило многоугольника Правило параллелепипеда
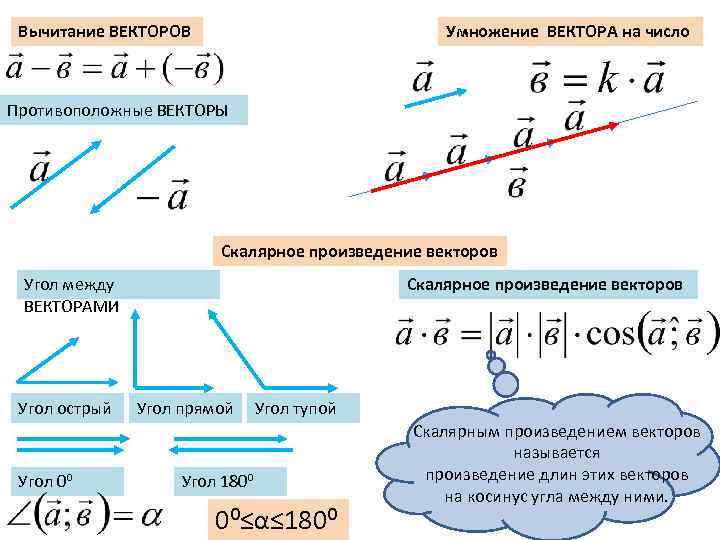 Вычитание ВЕКТОРОВ Умножение ВЕКТОРА на число Противоположные ВЕКТОРЫ Скалярное произведение векторов Угол между ВЕКТОРАМИ Угол острый Угол 0⁰ Скалярное произведение векторов Угол прямой Угол тупой Угол 180⁰ 0⁰≤α≤ 180⁰ Скалярным произведением векторов называется произведение длин этих векторов на косинус угла между ними.
Вычитание ВЕКТОРОВ Умножение ВЕКТОРА на число Противоположные ВЕКТОРЫ Скалярное произведение векторов Угол между ВЕКТОРАМИ Угол острый Угол 0⁰ Скалярное произведение векторов Угол прямой Угол тупой Угол 180⁰ 0⁰≤α≤ 180⁰ Скалярным произведением векторов называется произведение длин этих векторов на косинус угла между ними.
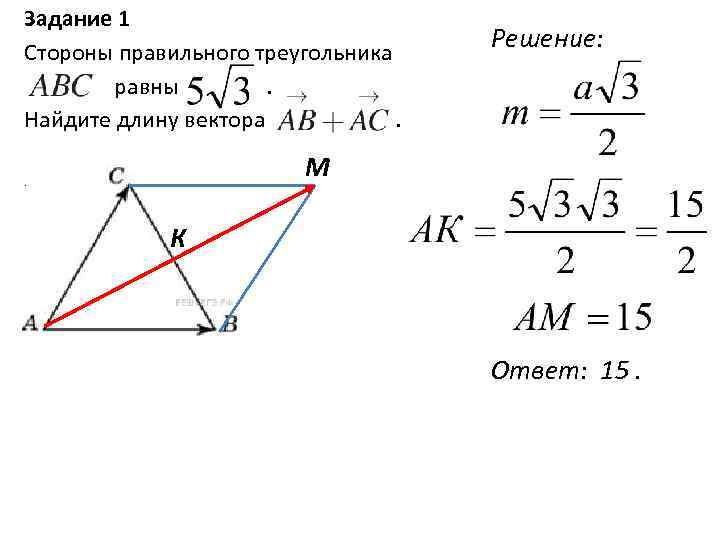 Задание 1 Стороны правильного треугольника равны . Найдите длину вектора . Решение: М . К Ответ: 15.
Задание 1 Стороны правильного треугольника равны . Найдите длину вектора . Решение: М . К Ответ: 15.
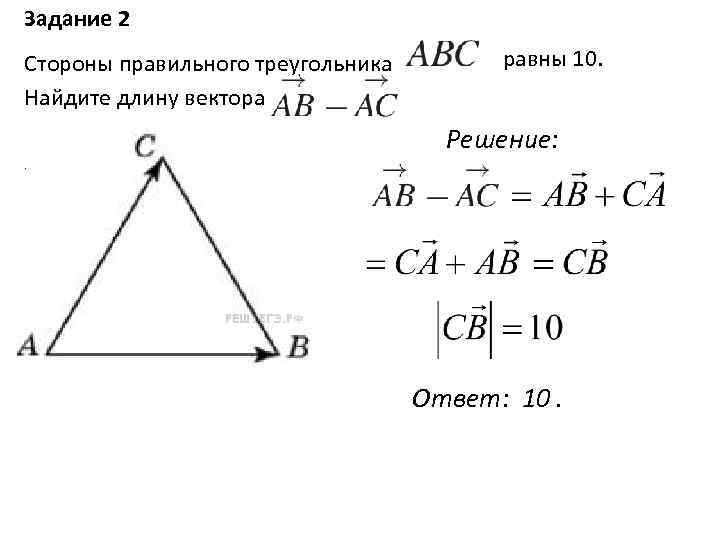 Задание 2 Стороны правильного треугольника Найдите длину вектора равны 10. Решение: . Ответ: 10.
Задание 2 Стороны правильного треугольника Найдите длину вектора равны 10. Решение: . Ответ: 10.
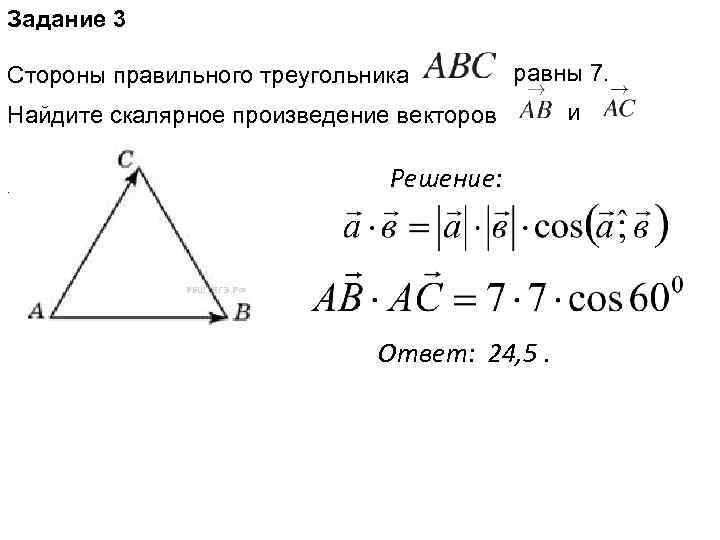 Задание 3 Стороны правильного треугольника равны 7. Найдите скалярное произведение векторов . Решение: Ответ: 24, 5. и
Задание 3 Стороны правильного треугольника равны 7. Найдите скалярное произведение векторов . Решение: Ответ: 24, 5. и
 Домашнее задание с урока 1: Учебник Геометрия 10 -11 кл. , п. 38 -45 (прочитать, составить краткую запись-конспект) Сайт «Решу ЕГЭ» позиция 3: № 27720, № 27721, № 27722.
Домашнее задание с урока 1: Учебник Геометрия 10 -11 кл. , п. 38 -45 (прочитать, составить краткую запись-конспект) Сайт «Решу ЕГЭ» позиция 3: № 27720, № 27721, № 27722.