7bc937196fecb12d6616f20fef07995e.ppt
- Количество слайдов: 54

Urban Freight Tour Models: State of the Art and Practice José Holguín-Veras, Ellen Thorson, Qian Wang, Ning Xu, Carlos González-Calderón, Iván Sánchez. Díaz, John Mitchell Center for Infrastructure, Transportation, and the Environment (CITE)

Outline v Introduction, Basic Concepts v Urban Freight Tours: Empirical Evidence v Urban Freight Tour Models v. Simulation Based Models v. Hybrid Models v. Analytical Models v Analytical Tour Models v Conclusions 2

3 Introduction and Basic Concepts
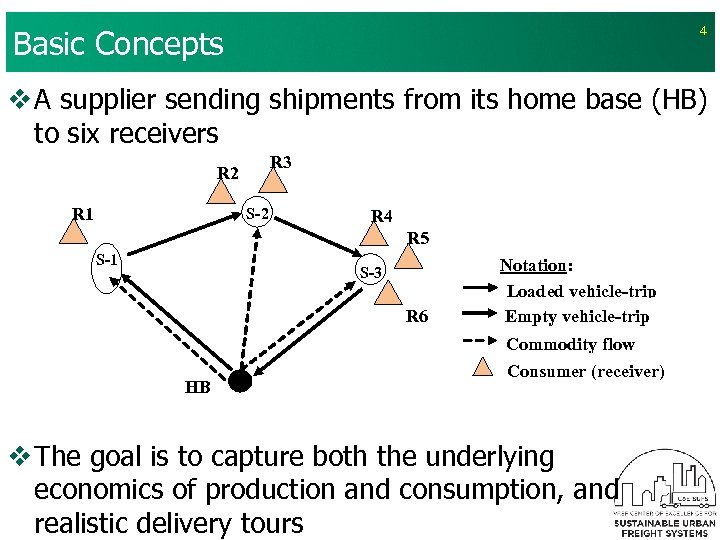
Basic Concepts 4 v A supplier sending shipments from its home base (HB) to six receivers R 2 R 1 R 3 S-2 R 4 R 5 S-1 Notation: Loaded vehicle-trip Empty vehicle-trip S-3 R 6 Commodity flow HB Consumer (receiver) v The goal is to capture both the underlying economics of production and consumption, and realistic delivery tours

5 Empirical Evidence on Urban Freight Tours
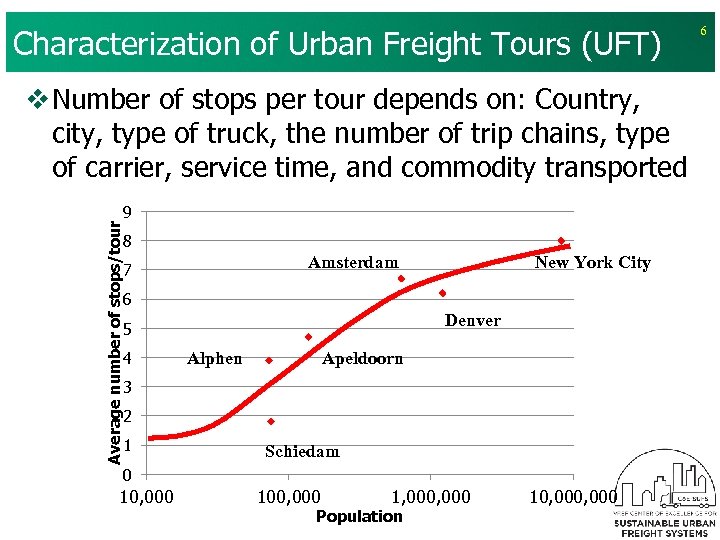
Characterization of Urban Freight Tours (UFT) Average number of stops/tour v Number of stops per tour depends on: Country, city, type of truck, the number of trip chains, type of carrier, service time, and commodity transported 9 8 New York City Amsterdam 7 6 Denver 5 4 Alphen Apeldoorn 3 2 1 Schiedam 0 10, 000 100, 000 1, 000 Population 10, 000 6
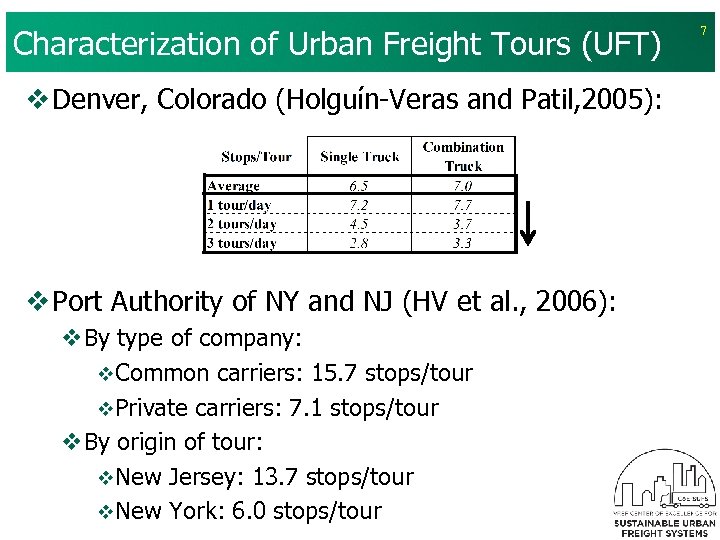
Characterization of Urban Freight Tours (UFT) v Denver, Colorado (Holguín-Veras and Patil, 2005): v Port Authority of NY and NJ (HV et al. , 2006): v. By type of company: v. Common carriers: 15. 7 stops/tour v. Private carriers: 7. 1 stops/tour v. By origin of tour: v. New Jersey: 13. 7 stops/tour v. New York: 6. 0 stops/tour 7
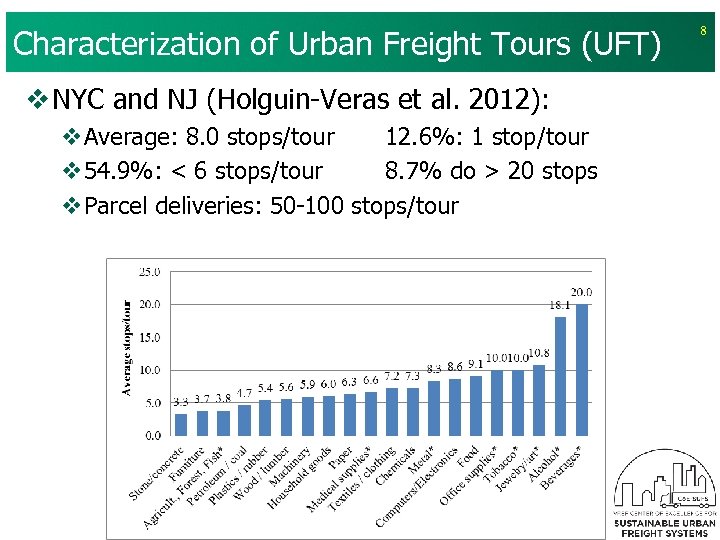
Characterization of Urban Freight Tours (UFT) v NYC and NJ (Holguin-Veras et al. 2012): v. Average: 8. 0 stops/tour 12. 6%: 1 stop/tour v 54. 9%: < 6 stops/tour 8. 7% do > 20 stops v. Parcel deliveries: 50 -100 stops/tour 8

9 Urban Freight Tour Models
Urban Freight Tour Models v The UFT models could be subdivided into: v. Simulation models v. Hybrid models v. Analytical models 10

11 Simulation Models

Simulation Models v Simulation models attempt to create the needed isomorphic relation between model and reality by imitating observed behaviors in a computer program v Examples include: v. Tavasszy et al. (1998) (SMILE) v. Boerkamps and van Binsbergen (1999) (Good. Trip) v. Ambrosini et al. , (2004) (FRETURB) v. Liedtke (2006) and Liedtke (2009) (INTERLOG) 12

13 Hybrid Models

Hybrid Models 14 v Hybrid models incorporate features of both simulation and analytical models (e. g. , using a gravity model to estimate commodity flows, and a simulation model to estimate the UFTs) v Examples include: vvan Duin et al. (2007) v. Wisetjindawat et al. (2007) v. Donnelly (2007)

15 Analytical Models

Analytical Models 16 v Analytical models attend to achieve isomorphism using formal mathematic representations based on behavioral, economic, or statistical axioms v Two main branches: v. Spatial Price equilibrium models (disaggregate) v. Entropy Maximization models (aggregate) v Examples include: v. Holguín-Veras (2000), Thorson (2005) v. Xu (2008), Xu and Holguín-Veras (2008) v. Holguín-Veras et al. (2012) v. Wang and Holguín-Veras (2009), Sanchez and Holguín-Veras (2012)

17 Entropy Maximization Tour Flow Model

Entropy Maximization Tour Flow Models 18 v Based on entropy maximization theory (Wilson, 1969; Wilson, 1970; Wilson, 1970) v Computes most likely solution given constraints v Key concepts: v. Tour sequence: An ordered listing of nodes visited v. Tour flow: The flow of vehicle-trips that follow a sequence v The problem is decomposed in two processes: v. A tour choice generation process v. A tour flow model
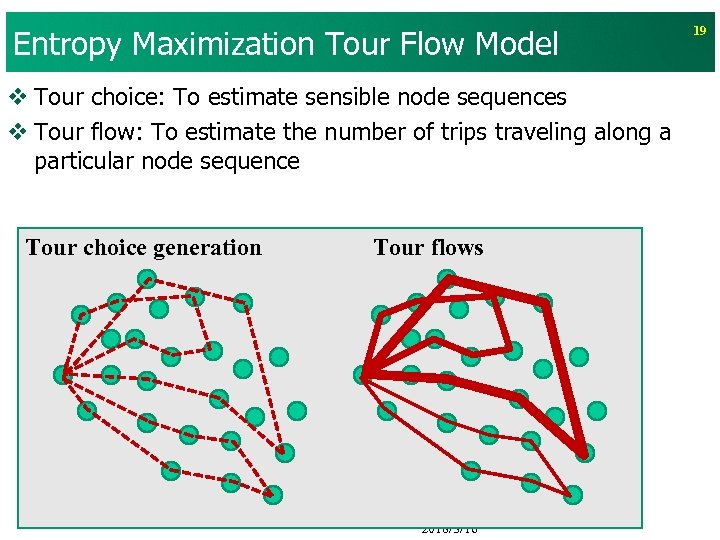
Entropy Maximization Tour Flow Model v Tour choice: To estimate sensible node sequences v Tour flow: To estimate the number of trips traveling along a particular node sequence Tour choice generation Tour flows 2018/3/16 19
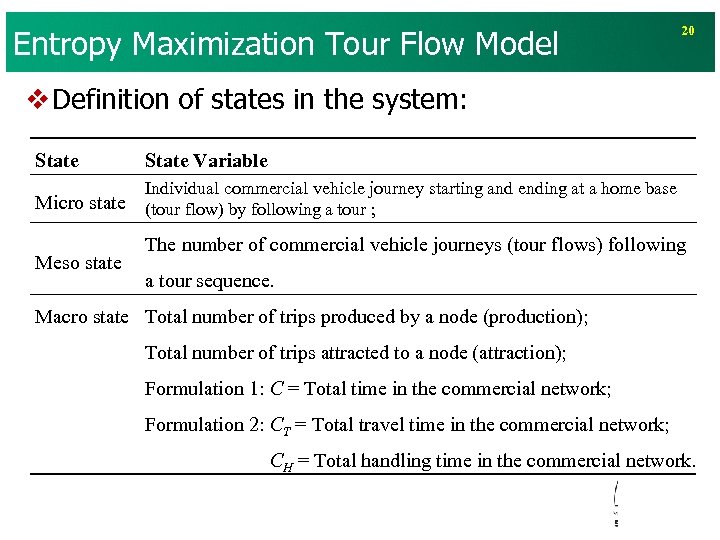
Entropy Maximization Tour Flow Model 20 v Definition of states in the system: State Variable Micro state Individual commercial vehicle journey starting and ending at a home base (tour flow) by following a tour ; Meso state The number of commercial vehicle journeys (tour flows) following a tour sequence. Macro state Total number of trips produced by a node (production); Total number of trips attracted to a node (attraction); Formulation 1: C = Total time in the commercial network; Formulation 2: CT = Total travel time in the commercial network; CH = Total handling time in the commercial network.

21 Static version of EM Tour Flow Model
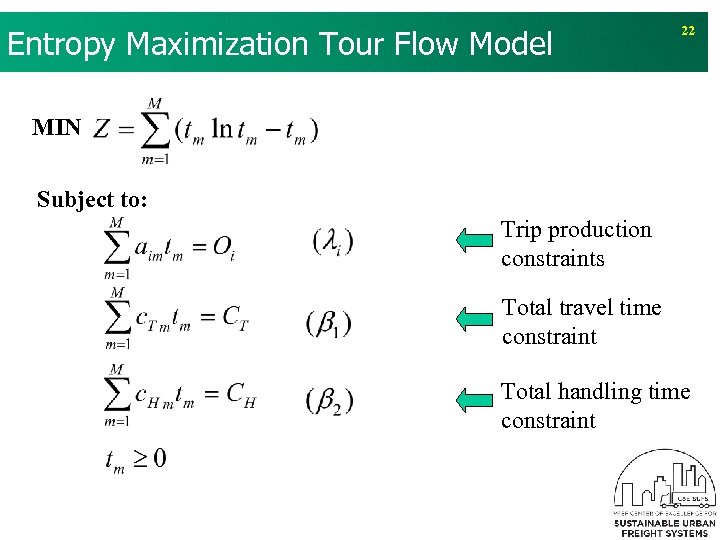
v The equivalent model of formulation 2: Entropy Maximization Tour Flow Model 22 MIN Subject to: Trip production constraints Total travel time constraint Total handling time constraint
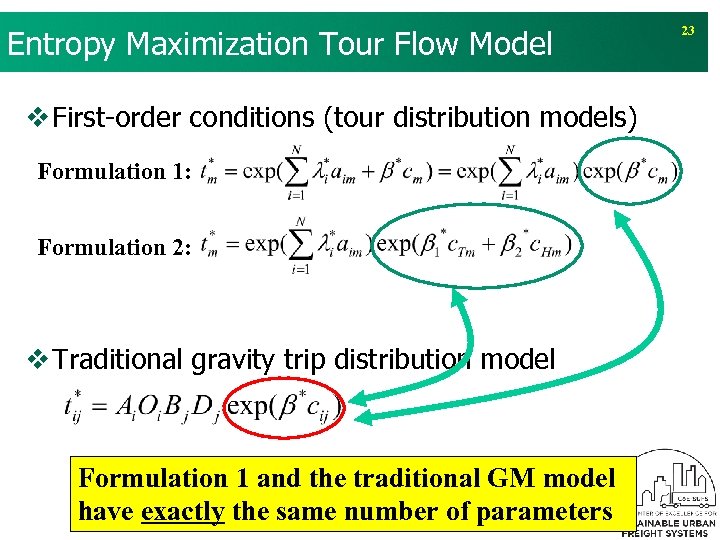
Entropy Maximization Tour Flow Model v First-order conditions (tour distribution models) Formulation 1: Formulation 2: v Traditional gravity trip distribution model Formulation 1 and the traditional GM model have exactly the same number of parameters 23

Entropy Maximization Tour Flow Model 24 v The optimal tour flows are found under the objective of maximizing the entropy for the system v The tour flows are a function of tour impedance and Lagrange multipliers associated with the trip productions and attractions along that tour v Successfully tested with Denver, Colorado, data: v. The MAPE of the estimated tour flows is less than 6. 7% given the observed tours are used v. Much better than the traditional GM

Case Study: Denver Metropolitan Area v Test network v 919 TAZs among which 182 TAZs contain home bases of commercial vehicles v 613 tours, representing a total of 65, 385 tour flows / day v. Calibration done with 17, 000 tours (from heuristics) v Estimation procedure v. Sorting input data: aggregate the observed tour flows to obtain trip productions and total impedance v. Estimation: estimate the tour flows distributed on these tours using the entropy maximization formulations v. Assessing performance: compare the estimated tour flows with the observed tour flows 25
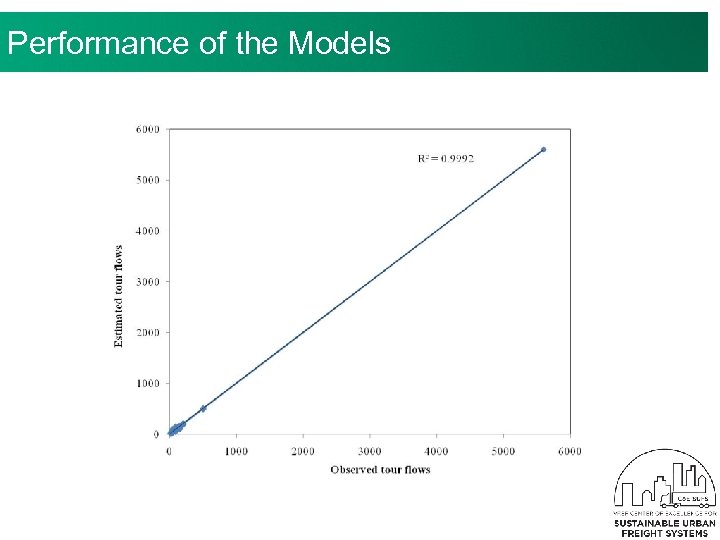
v Estimated vs. observed tour flows Performance of the Models

27 Time-Dependent Freight Tour Synthesis Model

TD-FTS Model 28 v Bi-objective Program: Possible combinations of flow Function to replicate TD traffic counts Trip Production Constraint I can drop Trip Attraction Constraint Impedance Constraint

TD-FTS Model 29 v Multi-attribute Value formulation: Utility function from DM Trip Production Constraint per Industry Impedance Constraint
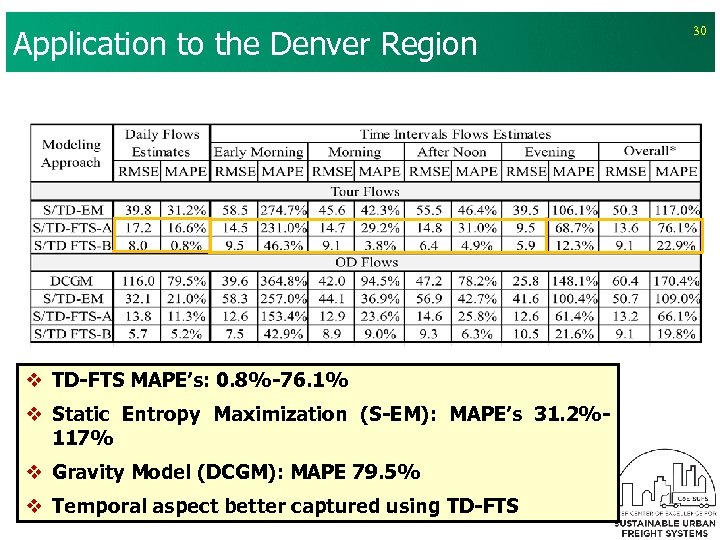
Application to the Denver Region v TD-FTS MAPE’s: 0. 8%-76. 1% v Static Entropy Maximization (S-EM): MAPE’s 31. 2%117% v Gravity Model (DCGM): MAPE 79. 5% v Temporal aspect better captured using TD-FTS 30
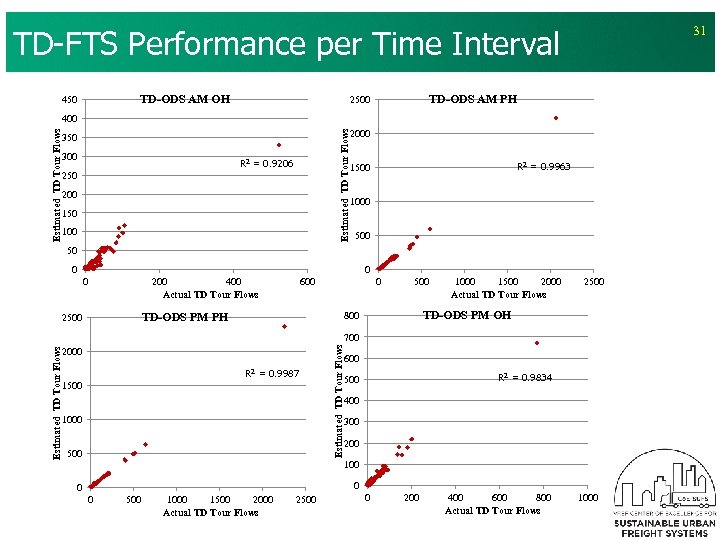
TD-FTS Performance per Time Interval TD-ODS AM OH 450 31 TD-ODS AM PH 2500 Estimated TD Tour Flows 400 350 300 R 2 = 0. 9206 250 200 150 100 2000 R 2 = 0. 9963 1500 1000 50 0 200 400 Actual TD Tour Flows 0 TD-ODS PM PH 500 2000 R 2 = 0. 9987 1500 1000 1500 2000 Actual TD Tour Flows 2500 TD-ODS PM OH 800 Estimated TD Tour Flows 2500 Estimated TD Tour Flows 600 700 600 R 2 = 0. 9834 500 400 300 200 100 0 500 1000 1500 2000 Actual TD Tour Flows 2500 0 200 400 600 800 Actual TD Tour Flows 1000

32 Multiclass Equilibrium Demand Synthesis

Multiclass traffic 33 v Multiclass: two or more classes of travelers with different behavioral or choice characteristics v Vehicle classes are related under the same objective function v Multiclass equilibrium demand synthesis (MEDS)

Link Travel Cost 34 v Travel time function depends on the vector of traffic flows for passenger cars and trucks v The travel cost is affected by the value of time of each one of the classes v The formula is a second order Taylor expansion of a general link-performance function Where: Xt: Vector of truck traffic flow Xc: Vector of passenger cars traffic flow

Multiclass Equilibrium 35 v In a multiclass equilibrium, the cost functions of the modes are asymmetric, traffic flows interact v The user optimal assignment cannot be written as an optimization problem v The User Equilibrium (UE) problem could be addressed using a Variational Inequality (VI) Problem

Link Travel Cost 36 v Although the vehicles share the transportation network and the travel time is the same (in equilibrium), the travel cost will be affected by the value of time of each one of the parties value of time v Considering paths, the cost functions for truck tours and passenger cars will be given by: In a multiclass equilibrium, the cost functions of modes are asymmetric, traffic flows interact. UE Variational Inequality Where: : A binary variable indicating whether tour m uses link a : A binary variable indicating whether trip from i to j uses link a

Multiclass EM Formulations v The multiclass EM formulations is given by: Where: W: System entropy that represents the number of ways of distributing commercial vehicles tour flows and passenger cars flows Tt: Total number of commercial vehicle tour flows in the network; Tc: Total number of passenger cars flows in the network; tm : Number of commercial vehicle journeys (tour flows) following tour m; Tij : Number of car trips between i and j 37

Multiclass Equilibrium ODS Formulations Min Subject to 38 The objective is to find the most likely ways to distribute tours considering congestion VI problem to obtain a UE condition for cars and trucks

39 Spatial Price Equilibrium Tour Models

General principles 40 v The models estimate commodity flows and vehicle trips that arise under competitive market equilibrium v Conceptual advantages: v. Account for tours v. Provide a coherent framework to jointly model the joint formation of commodity flows and vehicle trips v Based on the seminal work of Samuelson (1952), as it seeks to maximize the economic welfare associated with the consumption and transportation of the cargo, taking into account the formation of UFTs

Two flavors v Independent Shipper-Carrier Operations: v. Carrier and Shipper are independent companies v. Carrier travels empty from its base to pick up cargo at shipper’s location(s) v. Carrier delivers cargo to shipper’s customers v. Carrier travels empty back to its base v Integrated Shipper-Carrier Operations: v. Carrier and Shipper are part of the same company v. Carrier is loaded at shipper’s location(s) v. Carrier delivers cargo to shipper’s customers v. Carrier travels empty back to its base 41
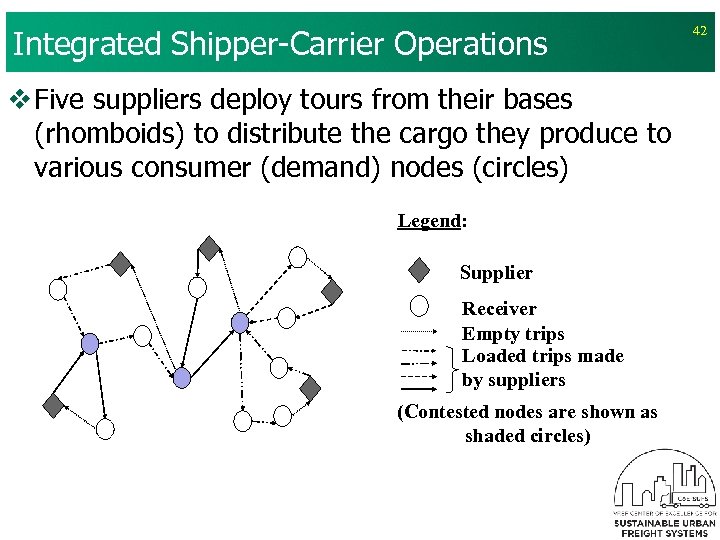
Integrated Shipper-Carrier Operations v Five suppliers deploy tours from their bases (rhomboids) to distribute the cargo they produce to various consumer (demand) nodes (circles) Legend: Supplier Receiver Empty trips Loaded trips made by suppliers (Contested nodes are shown as shaded circles) 42
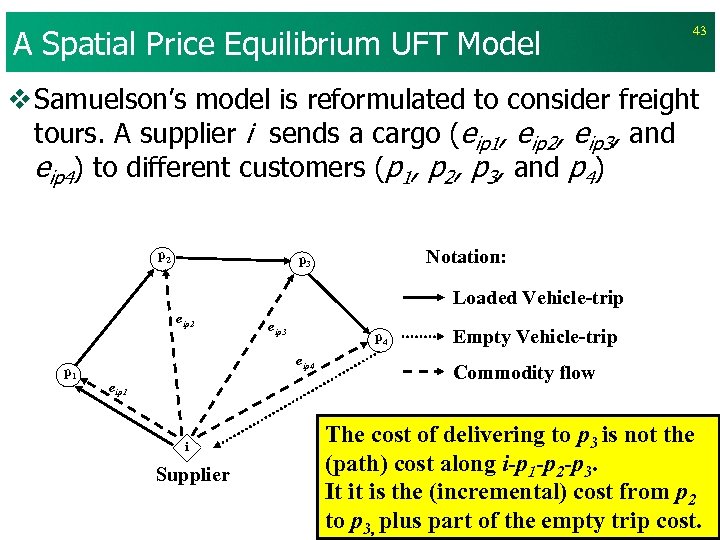
A Spatial Price Equilibrium UFT Model 43 v Samuelson’s model is reformulated to consider freight tours. A supplier i sends a cargo (eip 1, eip 2, eip 3, and eip 4) to different customers (p 1, p 2, p 3, and p 4) p 2 Notation: p 3 Loaded Vehicle-trip eip 2 p 1 eip 3 p 4 eip 1 i Supplier Empty Vehicle-trip Commodity flow The cost of delivering to p 3 is not the (path) cost along i-p 1 -p 2 -p 3. It it is the (incremental) cost from p 2 to p 3, plus part of the empty trip cost.

A Spatial Price Equilibrium UFT Model (P 1) 44 MAX (Social Welfare) Subject to: (Area under excess supply function) (Excess supply) (Delivery cost to demand node) (Linking flows to vehicle-trips) (Tour length constraint) This term is equal to the summation of tour costs. (Capacity constraint) Thus, it could be replaced by (Conservation of flow) the summation of tour costs, which allows to eliminate the (Integrality) delivery cost constraint (Non-negativity)

A Spatial Price Equilibrium UFT Model (P 2) 45 MAX (Net Social Payoff) Subject to: (Area under excess supply function) (Excess supply) (Linking flows to vehicle-trips) (Tour length constraint) (Capacity constraint) (Conservation of flow) (Integrality) (Non-negativity)

However… v P 2 is a nasty combinatorial and non-linear problem that is notoriously difficult to solve v To solve it, frame it as: v. A dispersed SPE problem v. A problem of profit maximization subject to competition (which is equivalent to the NSP formulation produced by Samuelson) v. A dynamic problem in which competitors adjust decisions based on the market competition results v Use heuristics 46
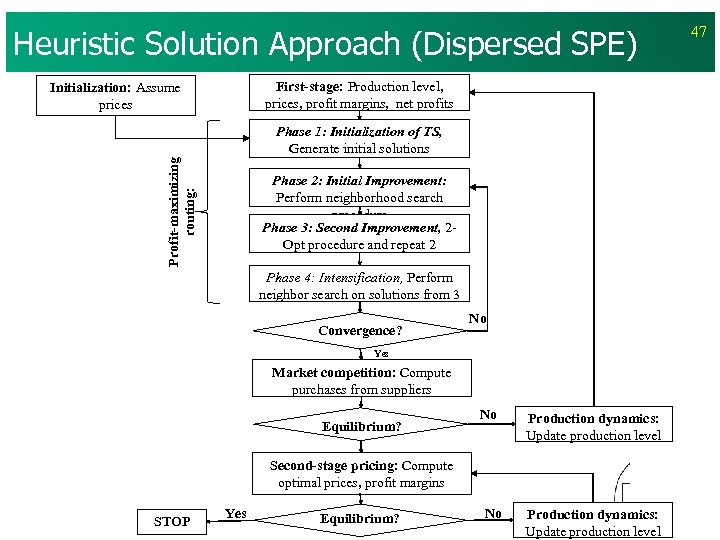
Heuristic Solution Approach (Dispersed SPE) First-stage: Production level, prices, profit margins, net profits Initialization: Assume prices Profit-maximizing routing: Phase 1: Initialization of TS, Generate initial solutions Phase 2: Initial Improvement: Perform neighborhood search procedure Phase 3: Second Improvement, 2 Opt procedure and repeat 2 Phase 4: Intensification, Perform neighbor search on solutions from 3 Convergence? No Yes Market competition: Compute purchases from suppliers Equilibrium? No Production dynamics: Update production level Second-stage pricing: Compute optimal prices, profit margins STOP Yes Equilibrium? No Production dynamics: Update production level 47
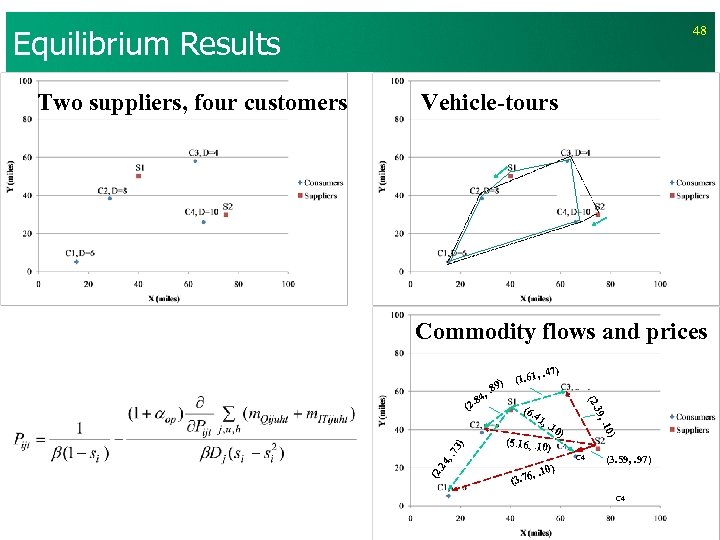
Equilibrium Results Vehicle-tours Commodity flows and prices 9) 41 , . 1 0) (5. 16, . 10 ) 0) 6, . 1 ) , . 7 3) (6. . 10 39, . 24 , . 47) (1. 61 (2. , . 8 84 (2. (2 Two suppliers, four customers 48 C 4 (3. 59, . 97) (3. 7 C 4

49 Concluding Remarks

Conclusions 50 v There are reasons to be optimistic: v. The community is cognizant of the need to model tours v. Collecting data and developing tour models v. However: v. The models developed are still in need of improvements v. The data collected are small and not comprehensive v Simulations and hybrid models require better behavioral foundations that are not always validated v The most theoretically appealing models present significant computational challenges to be overcome v Entropy Maximization models offer an interesting avenue, though disregarding commodity flows

51 References

References v v v v v 52 Ambrosini, C. , J. L. Routhier and F. Toilier (2004). How do urban policies work on the urban goods transport flows? WCTR, Istanbul. Boerkamps, J. and A. van Binsbergen (1999). Goodtrip - A New Approach for Modelling and Evaluation of Urban Goods Distribution. City Logistics I, Cairns, Australia. Donnelly, R. (2007). A hybrid microsimulation model of freight flows. Proceedings of the 4 th International Conference on City Logistics, July 11 -13, 2007. E. Taniguchi and R. G. Thompson. Crete, Greece, Institute for City Logistics: 235 -246. Figliozzi, M. A. (2007). "Analysis of the efficiency of urban commercial vehicle tours: Data collection, methodology, and policy implications. " ransportation Research Part T B: Methodological 41(9): 1014 -1032. Figliozzi, M. A. (2010). "The impacts of congestion on commercial vehicle tour characteristics and costs. " Transportation Research Part E: Logistics and Transportation Review 46(4): 496 -506. Holguín-Veras, J. (2000). A Framework for an Integrative Freight Market Simulation. IEEE 3 rd Annual Intelligent Transportation Systems Conference ITSC-2000, Dearborn Michigan, IEEE Holguín-Veras, J. (2002). "Revealed Preference Analysis of Commercial Vehicle Choice Process. " Journal of Transportation Engineering 128(4): 336. Holguín-Veras, J. (2008). "Necessary Conditions for Off-Hour Deliveries and the Effectiveness of Urban Freight Road Pricing and Alternative Financial Policies. " Transportation Research Part A: Policy and Practice 42 A(2): 392 -413. Holguín-Veras, J. (2011). "Urban Delivery Industry Response to Cordon Pricing, Time-Distance Pricing, and Carrier-Receiver Policies " Transportation Research Part A 45: 802 -824. Holguín-Veras, J. and G. Patil (2005). "Observed Trip Chain Behavior of Commercial Vehicles. " Transportation Research Record 1906: 74 -80. Holguín-Veras, J. and G. Patil (2007). "Integrated Origin-Destination Synthesis Model for Freight with Commodity-Based and Empty Trip Models. " Transportation Research Record 2008: 60 -66. Holguín-Veras, J. and G. Patil (2008). "A Multicommodity Integrated Freight Origin–destination Synthesis Model. " Networks and Spatial Economics 8(2): 309 -326. Holguín-Veras, J. , M. Silas and J. Polimeni (2008). An Investigation on the Attitudinal Factors Determining Participation in Cooperative Multi-Carrier Delivery Systems. Innovations in City Logistics IV. E. Taniguchi and R. Thomson, Nova Science Publishers: 55 -68. Holguín-Veras, J. , M. A. Silas, J. Polimeni and B. Cruz (2007). "An Investigation on the Effectiveness of Joint Receiver-Carrier Policies to Increase Truck Traffic in the Off. Peak Hours: Part I: The Behaviors of Receivers. " Networks and Spatial Economics 7(3): 277 -295. Holguín-Veras, J. , M. A. Silas, J. Polimeni and B. Cruz (2008). "An Investigation on the Effectiveness of Joint Receiver-Carrier Policies to Increase Truck Traffic in the Off. Peak Hours: Part II: The Behaviors of Carriers. " Networks and Spatial Economics 8(4): 327 -354. Holguín-Veras, J. , E. Thorson and J. Mitchell (2012). "Spatial Price Equilibrium Model of Independent Shipper-Carrier Operations with Explicit Consideration of Trip Chains. " Transportation Research Part B (in review). Holguín-Veras, J. , E. Thorson and K. Ozbay (2004). "Preliminary Results of Experimental Economics Application to Urban Goods Modeling Research. " Transportation Research Record: Journal of the Transportation Research Board 1873(-1): 9 -16. Holguín-Veras, J. and Q. Wang (2011). "Behavioral Investigation on the Factors that Determine Adoption of an Electronic Toll Collection System: Freight Carriers. " Transportation Research Part C 19(4): 593 -605. Holguín-Veras, J. , Q. Wang, N. Xu, K. Ozbay, M. Cetin and J. Polimeni (2006). "Impacts of Time of Day Pricing on the Behavior of Freight Carriers in a Congested Urban Area: Implications to Road Pricing. " Transportation Research Part A: Policy and Practice 40 (9): 744 -766.

References v v v v v 53 Holguín-Veras, J. , N. Xu and J. Mitchell (2012). "A Dynamic Spatial Price Equilibrium Model of Integrated Production-Transportation Operations Considering Freight Tours. " (in review). Hunt, J. D. and K. J. Stefan (2007). "Tour-based microsimulation of urban commercial movements. " Transportation Research Part B: Methodological 41(9): 981 -1013. Liedtke, G. (2006). An actor-based approach to commodity transport modelling. Ph. D. , Karlsruhe Universita t. Liedtke, G. (2009). "Principles of micro-behavior commodity transport modeling. " Transportation Research Part E: Logistics and Transportation Review 45(5): 795 -809. Mc. Fadden, D. , C. Winston and A. Boersch-Supan (1986). Joint Estimation of Freight Transportation Decisions Under Non-Random Sampling. Discussion Paper, Harvard University. Ruan, M. , J. Lin and K. Kawamura (2012). "Modeling urban commercial vehicle daily tour chaining. " Transportation Research Part E: Logistics and Transportation Review 48(6): 1169 -1184. Samuelson, P. A. (1952). "Spatial Price Equilibrium and Linear Programming. " American Economic Review 42(3): 283 -303. Samuelson, R. D. (1977). Modeling the Freight Rate Structure. Cambridge MA, Center for Transportation Studies, Massachusetts Institute of Technology. Stefan, K. , J. Mc. Millan and J. Hunt (2005). "Urban Commercial Vehicle Movement Model for Calgary, Alberta, Canada. " Transportation Research Record: Journal of the Transportation Research Board 1921: 1 -10. Tavasszy, L. A. , B. Smeenk and C. J. Ruijgrok (1998). "A DSS for Modelling Logistics Chains in Freight Transport Systems Analysis. " International Transactions in Operational Research 5(6): 447 -459. Thorson, E. (2005). The Integrative Freight Market Simulation: An Application of Experimental Economics and Algorithmic Solutions. Ph. D. , Rensselaer Polytechnic Institute. van Duin, J. H. R. , L. A. Tavasszy and E. Taniguchi (2007). "Real time simulation of auctioning and re-scheduling processes in hybrid freight markets. " Transportation Research Part B: Methodological 41(9): 1050 -1066. Vleugel, J. and M. Janic (2004). Route choice and the impact of ‘logistic routes’. Logistics Systems for Sustainable Cities. E. Taniguchi and R. Thompson, Elsevier. Wang, Q. (2008). Tour Based Urban Freight Travel Demand Models. Ph. D, Rensselaer Polytechnic Institute. Wang, Q. and J. Holguín-Veras (2008). "Investigation of Attributes Determining Trip Chaining Behavior in Hybrid Microsimulation Urban Freight Models. " Transportation Research Record: Journal of the Transportation Research Board 2066: 1 -8. Wang, Q. and J. Holguín-Veras (2009). Tour-based Entropy Maximization Formulations of Urban Commercial Vehicle Movements. 2009 Annual Meeting of the Transportation Research Board. CDROM. Wilson, A. G. (1969). "The use of entropy maximising models in theory of trip distribution, mode split " Journal of Transport Economics and Policy 108 -126. Wilson, A. G. (1970). Entropy in Urban and Regional Modelling. London, Pion. Wilson, A. G. (1970). "The use of the concept of entropy in system modelling. " Operational Research Quarterly 21(2): 247 -265. Wisetjindawat, W. , K. Sano, S. Matsumoto and P. Raothanachonkun (2007). Micro-Simulation Model for Modeling Freight Agents Interactions in Urban Freight Movement. 86 th Annual Meeting of the Transportation Research Board

54 Thanks! Questions?
7bc937196fecb12d6616f20fef07995e.ppt