УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА Простейшим представителем уравнения этого типа является уравнение теплопроводности 1
Уравнение теплопроводности для нестационарного случая 2
3
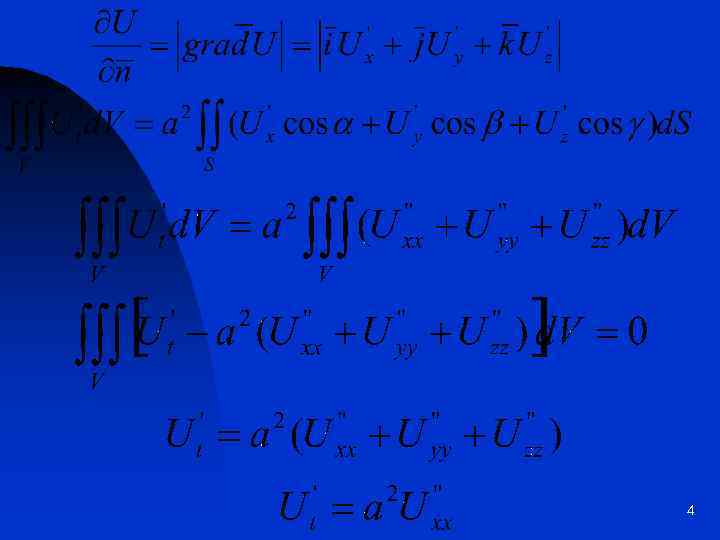
4
Закон Фурье для теплового потока: Закон Нернста для концентрации: 5
1. Первая краевая задача Найти решение уравнения, удовлетворяющее начальному условию U(x, 0) = f(x), в начальный момент времени (t = 0) задано распределение температуры по всей длине стержня (0 < x < l); и граничным условиям: U(0, t) = U 1, U(l, t) = U 2, на концах стержня (x = 0, x = l) и в любой момент времени известна температура U 1 и U 2. 6
2. Вторая краевая задача Найти решение уравнения, удовлетворяющее начальному условию U(x, 0) = f(x), в начальный момент времени (t = 0) задано распределение температуры по всей длине стержня (0 < x < l); и граничным условиям: U’x(0, t) = 0, U’x(l, t) = 0, концы стержня (x = 0, x = l) теплоизолированы. 7
3. Смешанная краевая задача Найти решение уравнения, удовлетворяющее начальному условию U(x, 0) = f(x), в начальный момент времени (t = 0) задано распределение температуры по всей длине стержня (0 < x < l); и граничным условиям: U’x(0, t) + h|Uc – U(0, t)| = 0, U’x(0, t) + h|Uc – U(l, t)| = 0, на концах стержня (x = 0, x = l) задан теплообмен со средой (температура среды Uс, h – коэффициент теплообмена. 8
4. Задача Коши Найти решение уравнения для бесконечного стержня, если известно начальное распределение температуры: U(x, 0) = f(x), -∞ < x < +∞, граничные условия отсутствуют. Можно рассматривать полубесконечный стержень x ≥ 0. Тогда на конце задается граничное условие (задача с одним граничным условием). Возможно ставить краевую задачу с условиями на разных концах (на одном конце задана температура, 9
Решение первой краевой задачи 10
Решение первой краевой задачи методом Фурье Для начала рассмотрим нулевые граничные условия 11
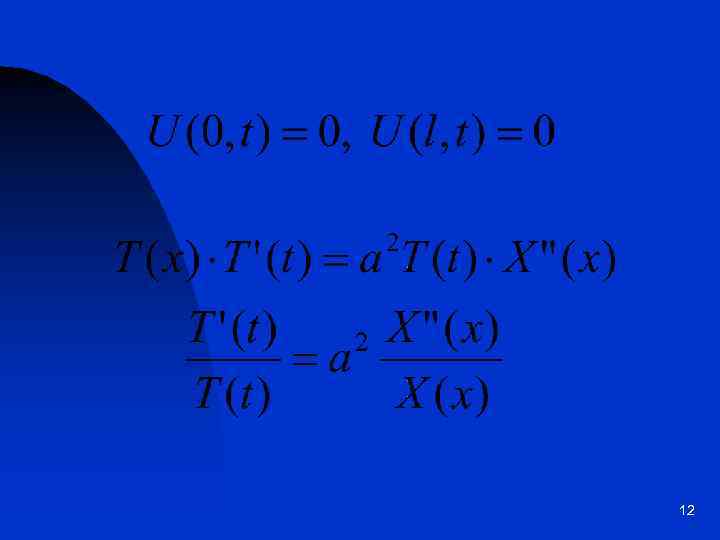
12
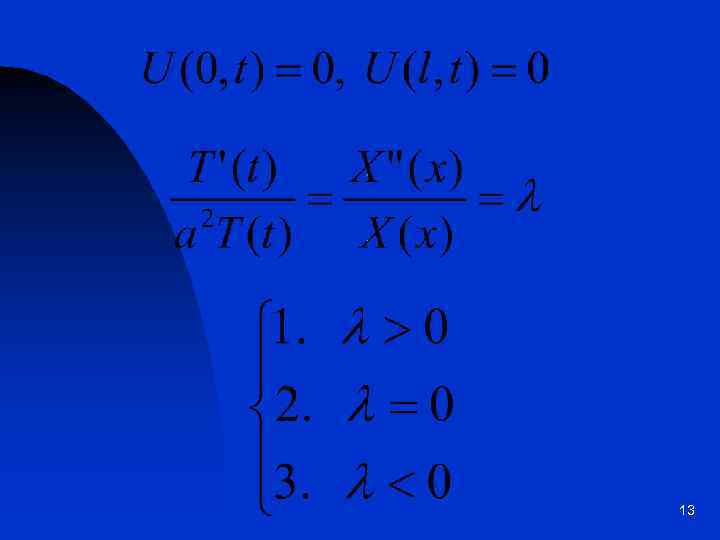
13
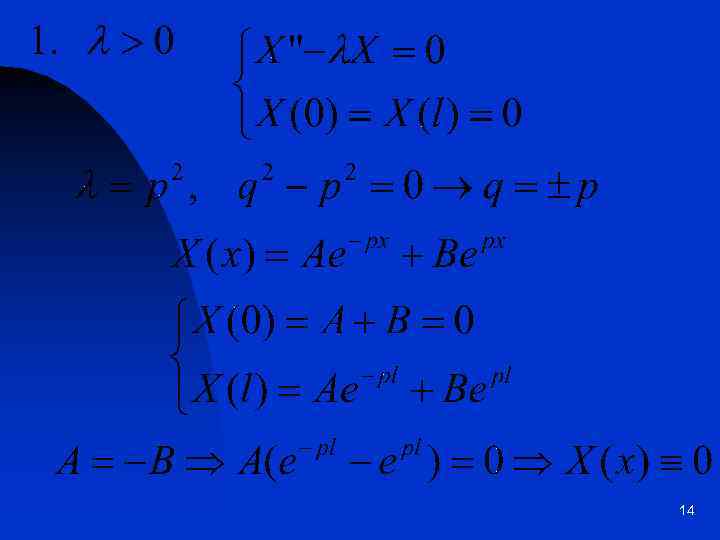
14
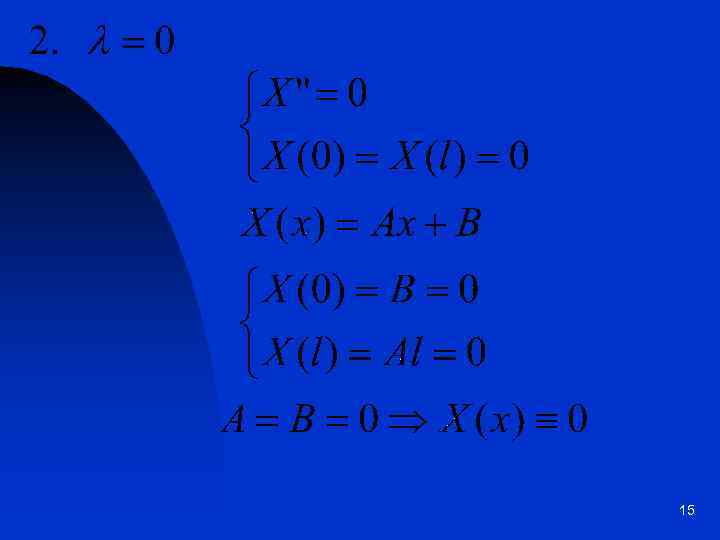
15
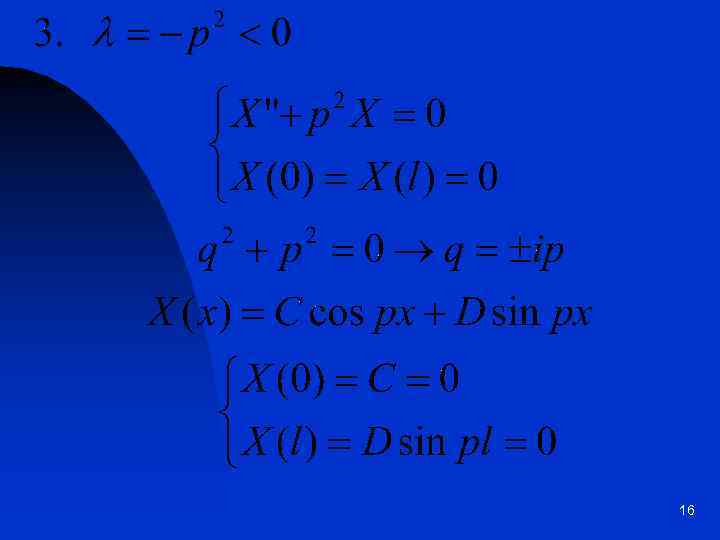
16
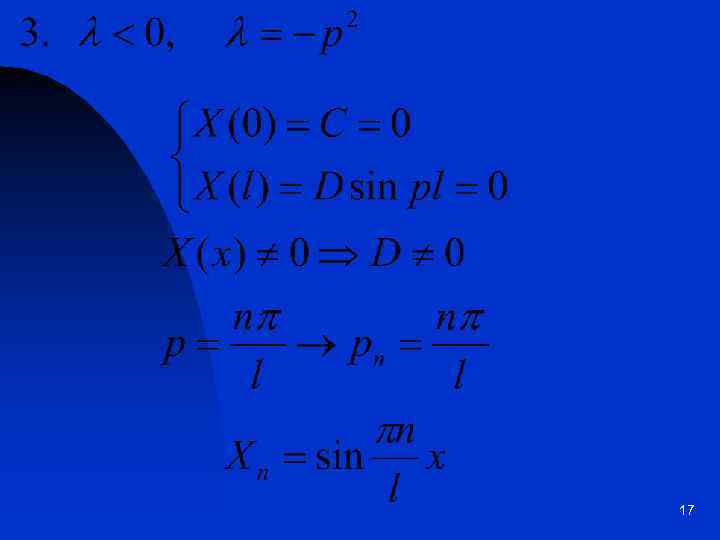
17
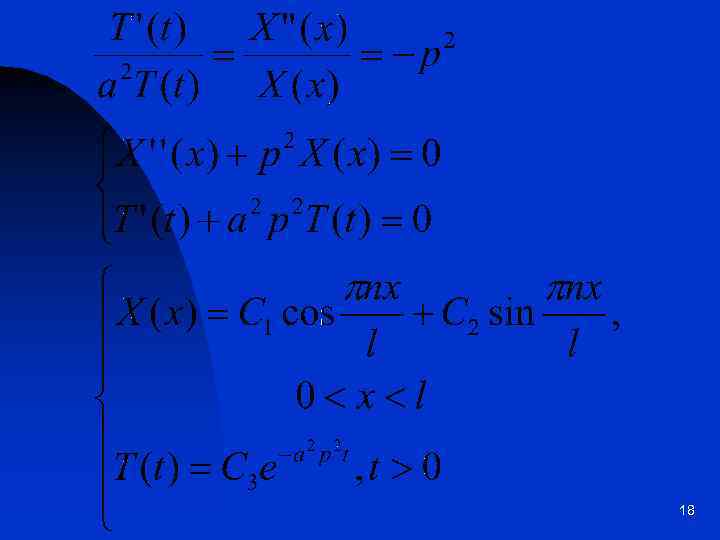
18
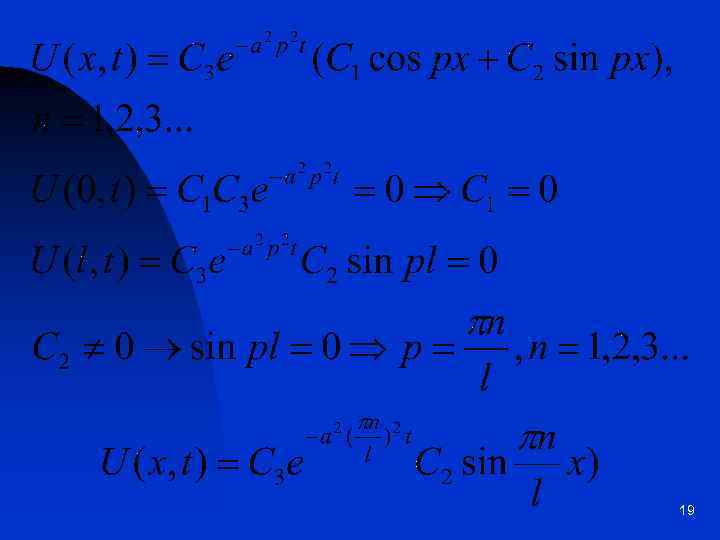
19
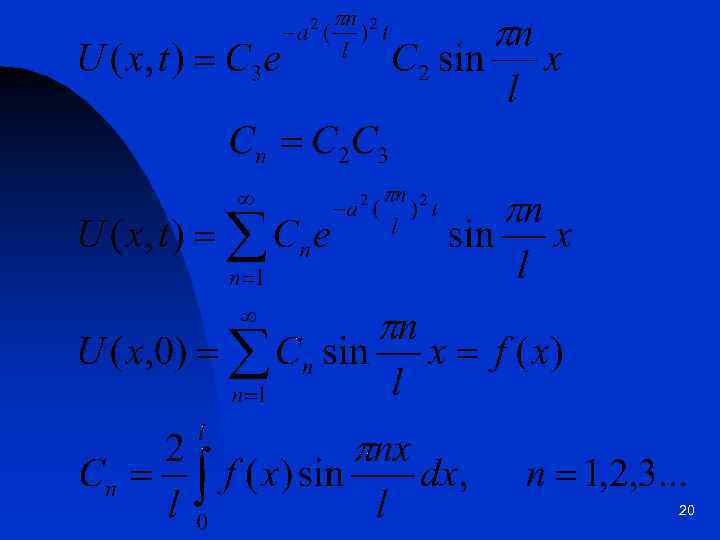
20
Найдем решение первой краевой задачи с ненулевыми граничными условиями, т. е. решение начальной задачи где n(x, t) – решение уравнения теплопроводности с нулевыми граничными условиями, а второе слагаемое – решение стационарного уравнения: называемое стационарной температурой, соответствующее ненулевым граничным условиям U(0, t) = U 1, U(l, t) = U 2. 21
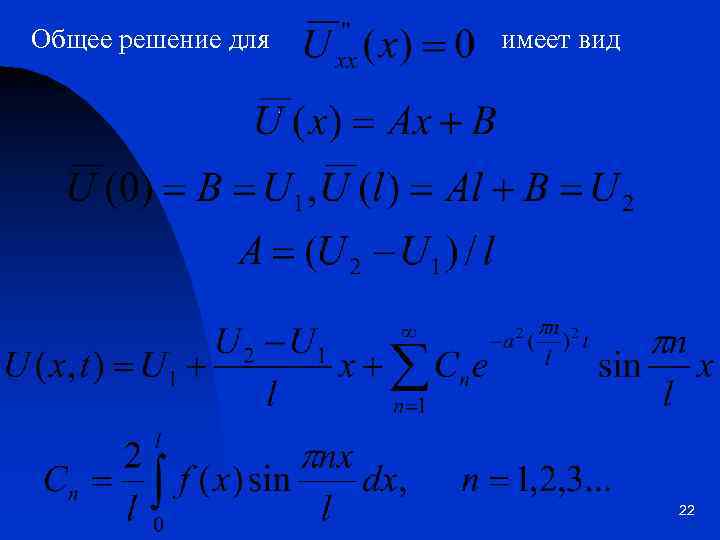
Общее решение для имеет вид 22
23
2. Вторая краевая задача Найти решение уравнения, удовлетворяющее началь-ному условию и граничным условиям 24
Метод Фурье для решения второй краевой задачи 25
26
27
![Рассматривая последнее равенство как разложение в ряд Фурье четной на отрезке [-l, l] периодической](https://present5.com/presentation/96839059_150881132/image-28.jpg "Рассматривая последнее равенство как разложение в ряд Фурье четной на отрезке [-l, l] периодической")
Рассматривая последнее равенство как разложение в ряд Фурье четной на отрезке [-l, l] периодической функции f(x), найдем коэффициенты разложения в виде: 28
Скачать презентацию УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА Простейшим представителем уравнения этого типа
UMF_L4N.ppt