Уравнение неразрывности непрерывности или закон сохранения массы 1

Уравнение неразрывности (непрерывности) или закон сохранения массы 1

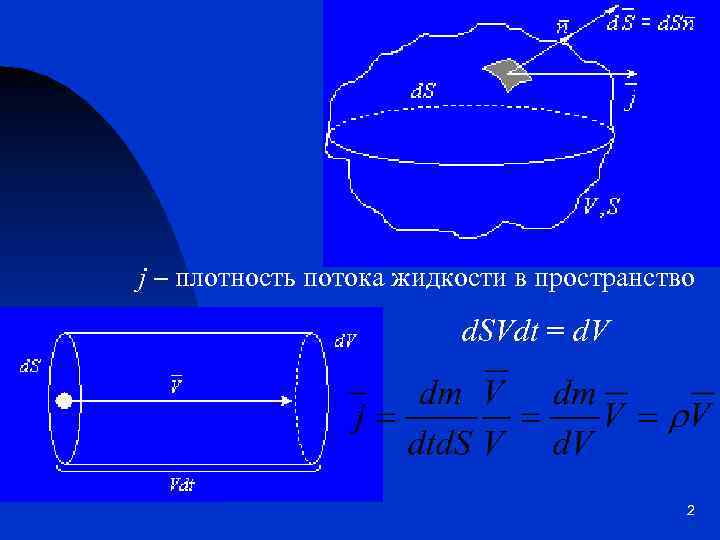j – плотность потока жидкости в пространство d. SVdt = d. V 2

- переход по формуле Остроградского-Гаусса. 3

Пусть t → 0, тогда 4

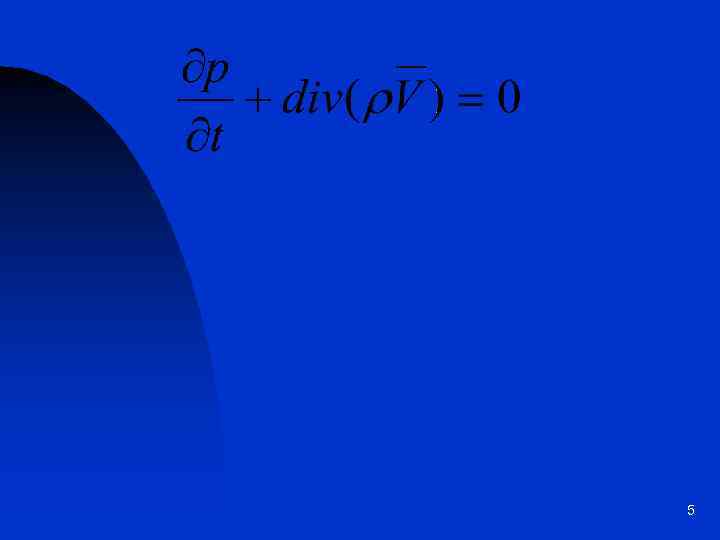5

Колебания круглой мембраны (двумерное волновое уравнение в круге) 6

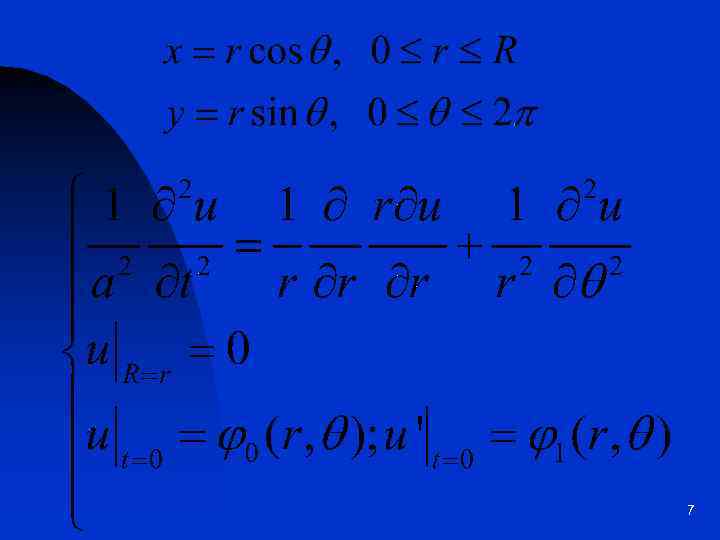7

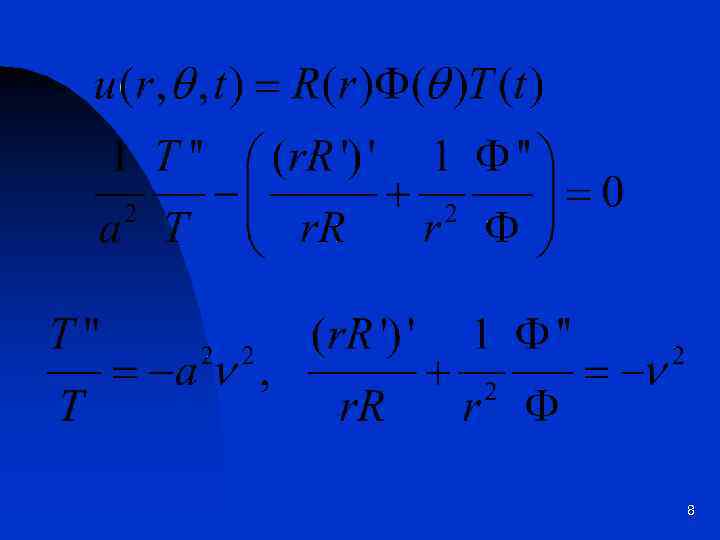8

Постоянная с не может быть произвольной, в силу того, что Ф – функция периодическая. Необходимо потребовать, чтобы с = -k 2. 9

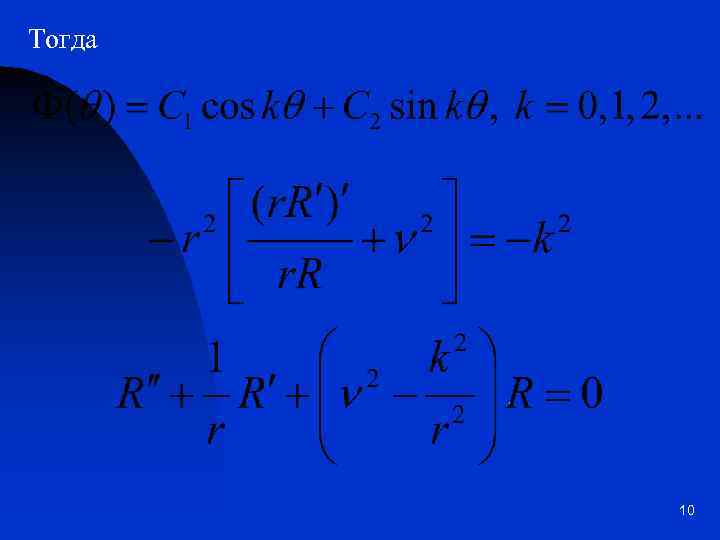Тогда 10

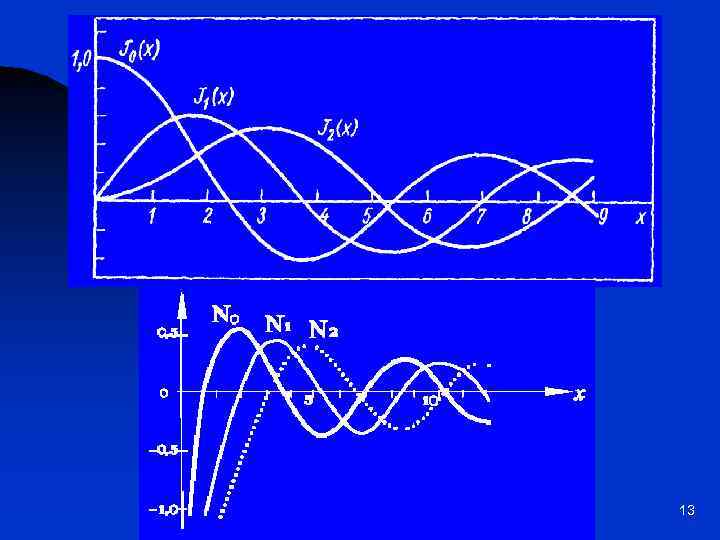
Специальные функции. Функции Бесселя 11

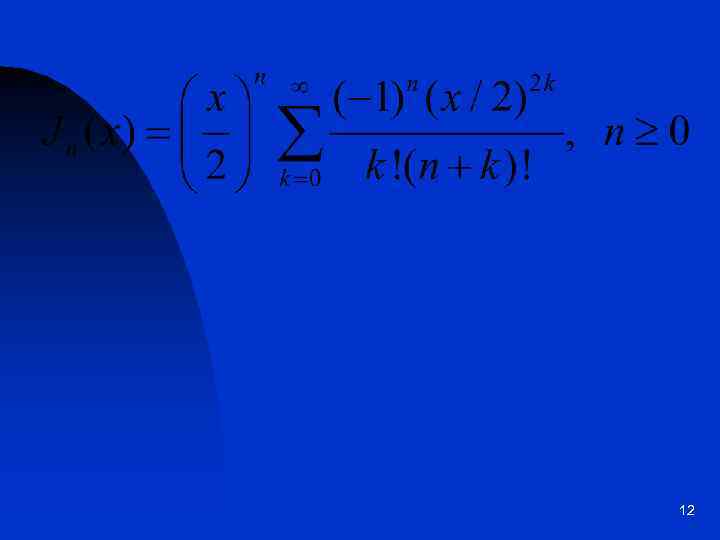12

13

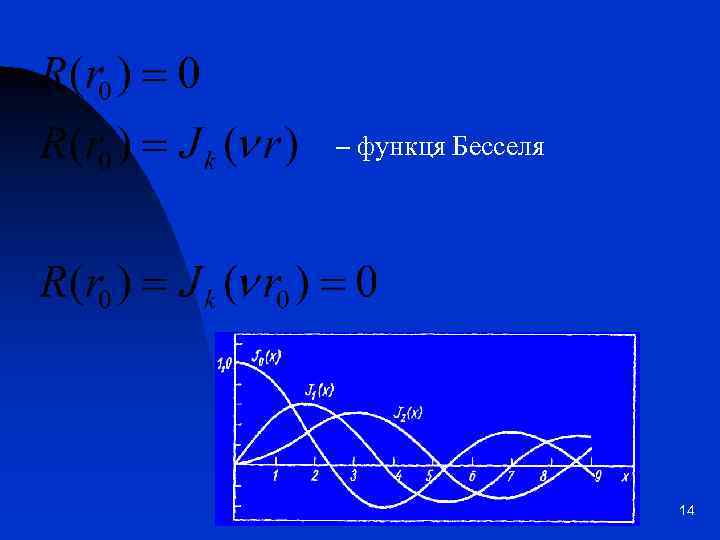– функця Бесселя 14

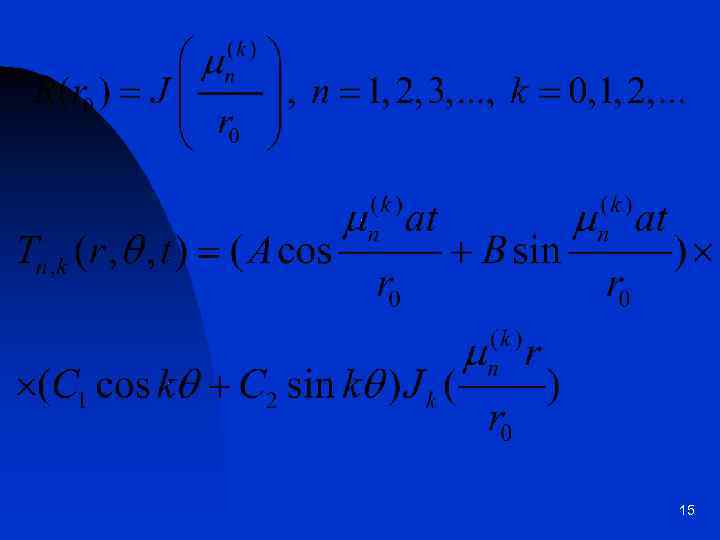15

16

Уравнение теплопроводности и диффузии – поле температуры [концентрации] Закон Фурье для теплового потока: Закон Нернста для концентрации: Поток тепла через S за время Dt: 17

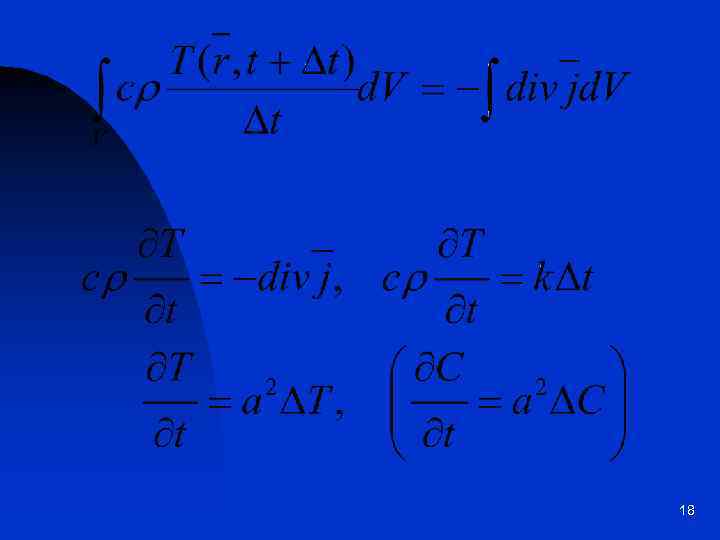18

Стационарный случай, когда Т = const: Это неоднородное и однородное уравнения Лапласа 19

20

УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ (для нестационарного случая) – производная функции U по направлению внешней нормали к поверхности S Так как теплота распространяется в направлении понижения температуры, то 21

Вычислим Q другим способом. Выделим элемент объема V, ограниченного поверхностью S. Количество теплоты d. Q, получаемой элементом d. V за время dt, пропорционально повышению температуры в этом элементе и массе самого элемента, т. е. 22

23

1. Первая краевая задача Найти решение уравнения, удовлетворяющее началь-ному условию и граничным условиям 24

Решение первой краевой задачи методом Фурье Вначале рассмотрим нулевые граничные условия: 25

26

Из краевых условия имеем: 27

Коэффициенты Сn для каждого n определим из начального условия: 28

Рассматривая как разложение в ряд Фурье нечетной на отрезке [-l, l] периодической функции f(x), найдем коэффициенты разложения в виде: 29

Найдем решение первой краевой задачи с ненулевыми граничными условиями, т. е. решение начальной задачи где n(x, t) – решение уравнения теплопроводности с нулевыми граничными условиями, а второе слагаемое – решение стационарного уравнения: называемое стационарной температурой, соответствующее ненулевым граничным условиям T(0, t) = T 1, T(l, t) = T 2. 30

Общее решение для имеет вид 31

2. Вторая краевая задача Найти решение уравнения, удовлетворяющее началь-ному условию и граничным условиям 32

Метод Фурье для решения второй краевой задачи 33

34

35

Рассматривая последнее равенство как разложение в ряд Фурье четной на отрезке [-l, l] периодической функции f(x), найдем коэффициенты разложения в виде: 36