2- Продольные и поперечные эффекты..ppt
- Количество слайдов: 34
 Уравнение Ландау-Лифшица. Тензор магнитной проницаемости и восприимчивости. • • • Из каких соображений было получено уравнение Ландау. Лифшица? Что следует из этого уравнения? Что описывает это уравнение? Что мы получили с помощью этого уравнения? Зачем уравнение Ландау-Лифшица вводят релаксационный член? Что такое ферромагнитный резонанс? Какова структура тензора магнитной восприимчивости? Как зависят от частоты действительная и мнимая компоненты тензора магнитной восприимчивости? Какова величина диагональной компоненты тензора μ на оптических частотах?
Уравнение Ландау-Лифшица. Тензор магнитной проницаемости и восприимчивости. • • • Из каких соображений было получено уравнение Ландау. Лифшица? Что следует из этого уравнения? Что описывает это уравнение? Что мы получили с помощью этого уравнения? Зачем уравнение Ландау-Лифшица вводят релаксационный член? Что такое ферромагнитный резонанс? Какова структура тензора магнитной восприимчивости? Как зависят от частоты действительная и мнимая компоненты тензора магнитной восприимчивости? Какова величина диагональной компоненты тензора μ на оптических частотах?
 Продольные и поперечные магнитооптические эффекты. • Распространение электромагнитной волны в среде. Уравнения Максвелла • Показатель преломления при продольном распространении волны üГироэлектрическая, гиромагнитная и бигиротропная среды ü Частотно независимый эффект Фарадея • Показатель преломления при поперечном распространении волны
Продольные и поперечные магнитооптические эффекты. • Распространение электромагнитной волны в среде. Уравнения Максвелла • Показатель преломления при продольном распространении волны üГироэлектрическая, гиромагнитная и бигиротропная среды ü Частотно независимый эффект Фарадея • Показатель преломления при поперечном распространении волны
 Тензор магнитной проницаемости Поправка к 1 в диагональной компоненте Недиагональная компонента
Тензор магнитной проницаемости Поправка к 1 в диагональной компоненте Недиагональная компонента
 Уравнения Максвелла
Уравнения Максвелла
 Электромагнитная волна ; α, β и γ – направляющие косинусы электромагнитной волны. n – комплексный показатель преломления.
Электромагнитная волна ; α, β и γ – направляющие косинусы электромагнитной волны. n – комплексный показатель преломления.
 Вектор
Вектор
 Вектор
Вектор

 Компоненты
Компоненты
 Имеем уравнения
Имеем уравнения
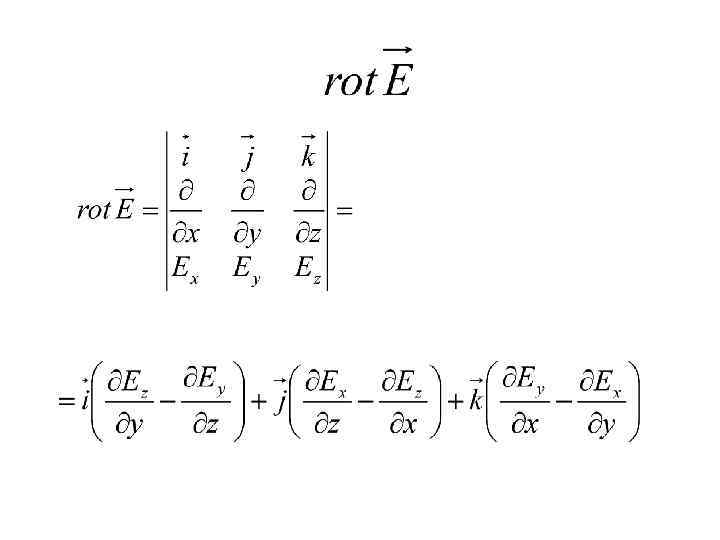
 Компоненты
Компоненты
 Имеем уравнения
Имеем уравнения
 Система уравнений для компонент векторов и
Система уравнений для компонент векторов и
 Расположим компоненты векторов и по порядку
Расположим компоненты векторов и по порядку
 Однородная система имеет решение, если ее определитель равен нулю
Однородная система имеет решение, если ее определитель равен нулю
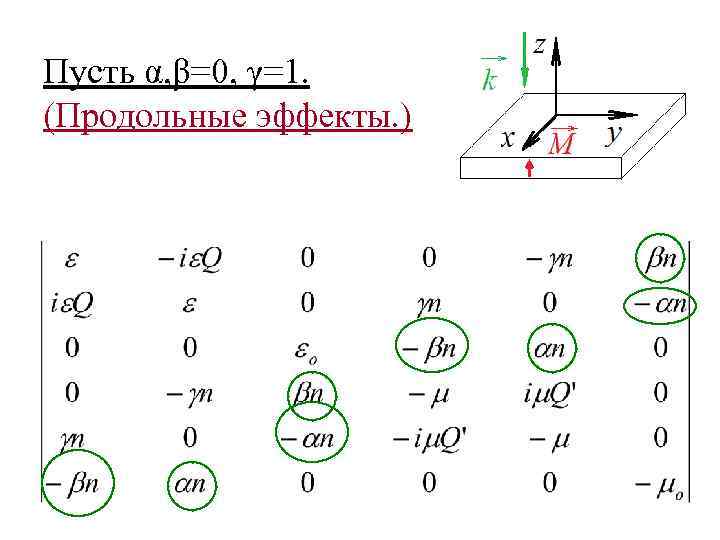 Пусть α, β=0, γ=1. (Продольные эффекты. )
Пусть α, β=0, γ=1. (Продольные эффекты. )
 Пусть α, β=0, γ=1. (Продольные эффекты. ) По шестой строке и шестому столбцу
Пусть α, β=0, γ=1. (Продольные эффекты. ) По шестой строке и шестому столбцу
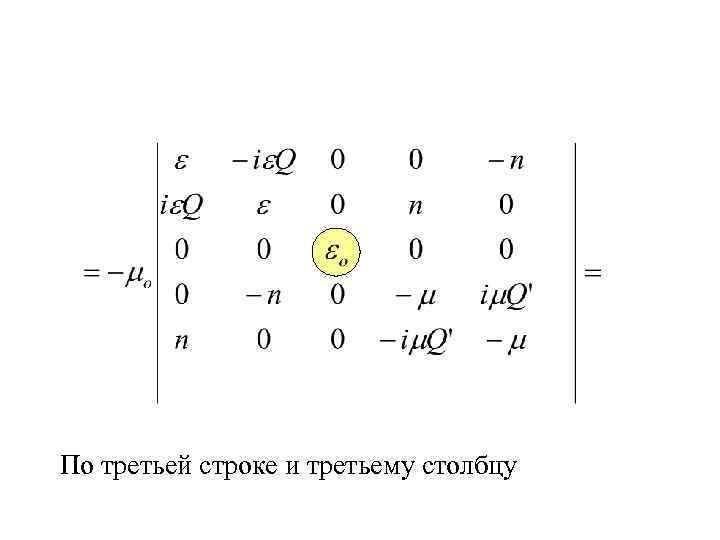 По третьей строке и третьему столбцу
По третьей строке и третьему столбцу
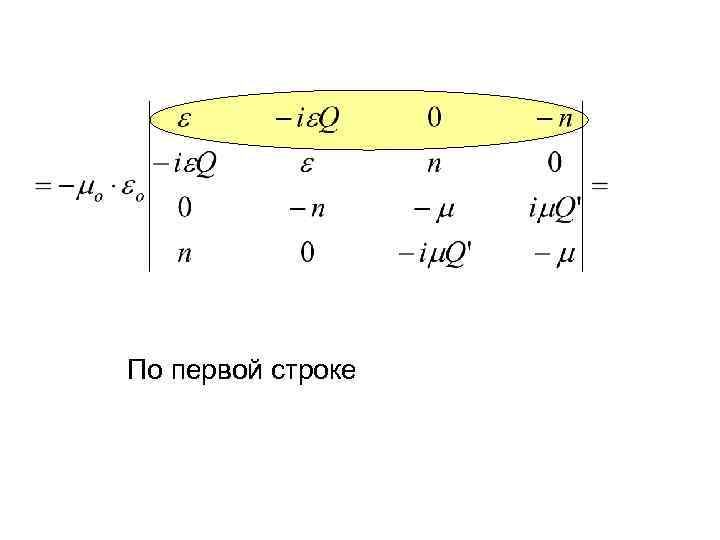 По первой строке
По первой строке
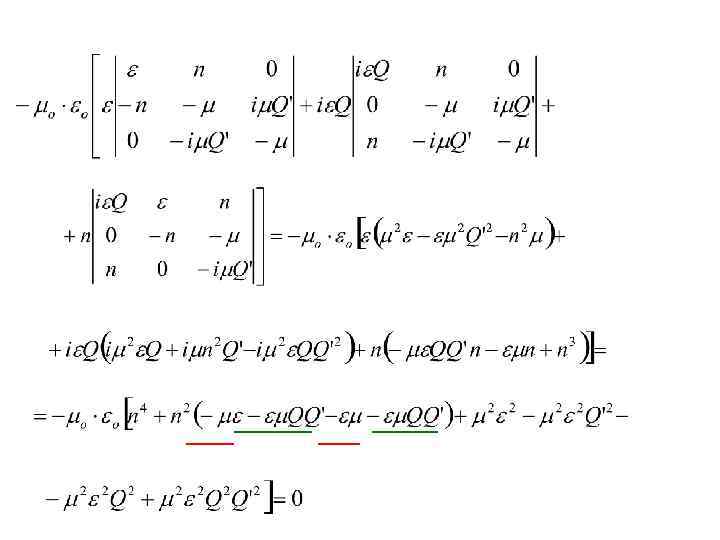
 Имеем биквадратное уравнение относительно n 0
Имеем биквадратное уравнение относительно n 0
 Поворот плоскости поляризации d – толщина пластинки, n – показатель преломления Учтем, что
Поворот плоскости поляризации d – толщина пластинки, n – показатель преломления Учтем, что
 Поворот плоскости поляризации Для бигиротропной среды Для гироэлектрической среды Для гиромагнитной среды Напомним, что
Поворот плоскости поляризации Для бигиротропной среды Для гироэлектрической среды Для гиромагнитной среды Напомним, что
 Вращение плоскости поляризации в гиромагнитной среде Учитывая, что следовательно При ω>>ωo Вращение плоскости поляризации в гиромагнитной среде не зависит от длины волны
Вращение плоскости поляризации в гиромагнитной среде Учитывая, что следовательно При ω>>ωo Вращение плоскости поляризации в гиромагнитной среде не зависит от длины волны
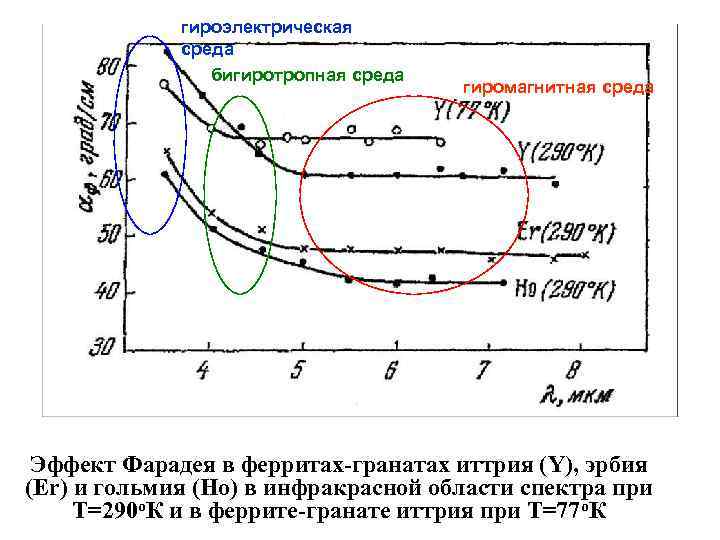 гироэлектрическая среда бигиротропная среда гиромагнитная среда Эффект Фарадея в ферритах-гранатах иттрия (Y), эрбия (Er) и гольмия (Ho) в инфракрасной области спектра при Т=290 о. К и в феррите-гранате иттрия при Т=77 о. К
гироэлектрическая среда бигиротропная среда гиромагнитная среда Эффект Фарадея в ферритах-гранатах иттрия (Y), эрбия (Er) и гольмия (Ho) в инфракрасной области спектра при Т=290 о. К и в феррите-гранате иттрия при Т=77 о. К
![Продольные эффекты. Нельзя разделить вклады тензоров [ε] и [μ] Продольные эффекты. Нельзя разделить вклады тензоров [ε] и [μ]](https://present5.com/presentation/138833089_336275805/image-27.jpg) Продольные эффекты. Нельзя разделить вклады тензоров [ε] и [μ]
Продольные эффекты. Нельзя разделить вклады тензоров [ε] и [μ]
 Однородная система имеет решение, если ее определитель равен нулю
Однородная система имеет решение, если ее определитель равен нулю
 Пусть α, β≠ 0, γ=0. (Поперечные эффекты. )
Пусть α, β≠ 0, γ=0. (Поперечные эффекты. )
 α, β≠ 0, γ=0. (Поперечные эффекты. )
α, β≠ 0, γ=0. (Поперечные эффекты. )
 Учитывая, что получим уравнение: S – волна (Hz=0, Hx, Hy≠ 0); вектор Е ┴ плоскости падения света P – волна (Hz≠ 0, Hx, Hy=0), Е ║ плоскости падения света Вклад в эффект Керра для гироэлектрической среды – 10 -3, для гиромагнитной – 10 -5.
Учитывая, что получим уравнение: S – волна (Hz=0, Hx, Hy≠ 0); вектор Е ┴ плоскости падения света P – волна (Hz≠ 0, Hx, Hy=0), Е ║ плоскости падения света Вклад в эффект Керра для гироэлектрической среды – 10 -3, для гиромагнитной – 10 -5.
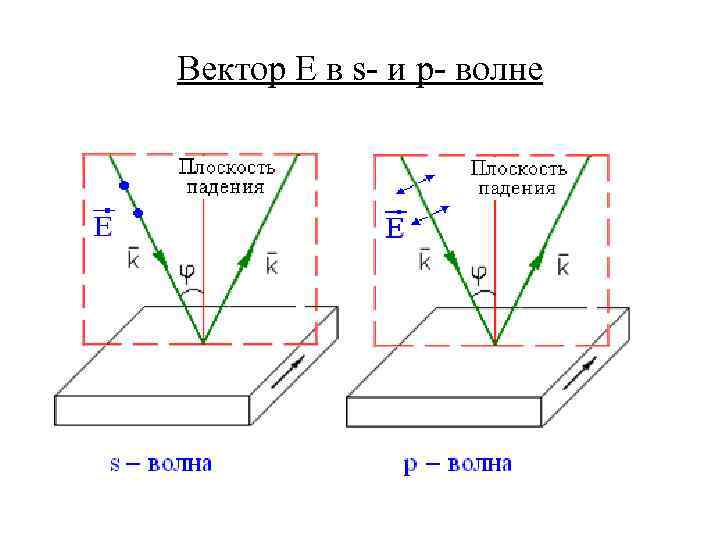 Вектор Е в s- и p- волне
Вектор Е в s- и p- волне
 Показатели преломления Для продольных эффектов Для поперечных эффектов
Показатели преломления Для продольных эффектов Для поперечных эффектов
 Продольные и поперечные магнитооптические эффекты. • Распространение электромагнитной волны в среде. Уравнения Максвелла • Показатель преломления при продольном распространении волны üГироэлектрическая, гиромагнитная и бигиротропная среды ü Частотно независимый эффект Фарадея • Показатель преломления при поперечном распространении волны
Продольные и поперечные магнитооптические эффекты. • Распространение электромагнитной волны в среде. Уравнения Максвелла • Показатель преломления при продольном распространении волны üГироэлектрическая, гиромагнитная и бигиротропная среды ü Частотно независимый эффект Фарадея • Показатель преломления при поперечном распространении волны


