Уравнение касательной к графику функции Повторение: вычисление

Уравнение касательной к графику функции

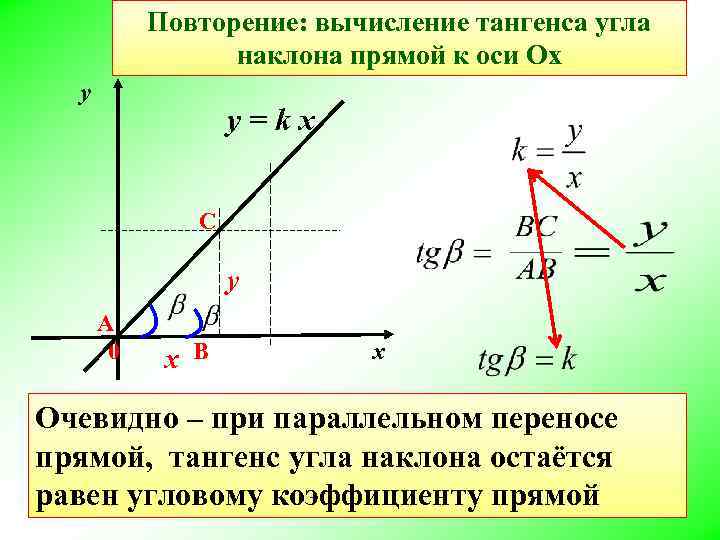Повторение: вычисление тангенса угла наклона прямой к оси Ох у y = k x С у А 0 х В х Очевидно – при параллельном переносе прямой, тангенс угла наклона остаётся равен угловому коэффициенту прямой

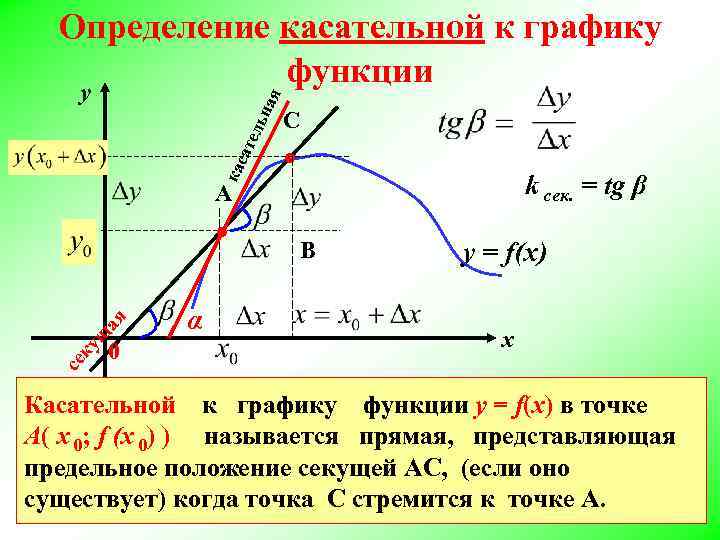Определение касательной к графику функции кас ате льн а я у С ● k сек. = tg β A се ку щ ая ● 0 α В у = f(x) х Касательной к графику функции y = f(x) в точке А( х 0; f (х 0) ) называется прямая, представляющая предельное положение секущей АС, (если оно существует) когда точка С стремится к точке А.

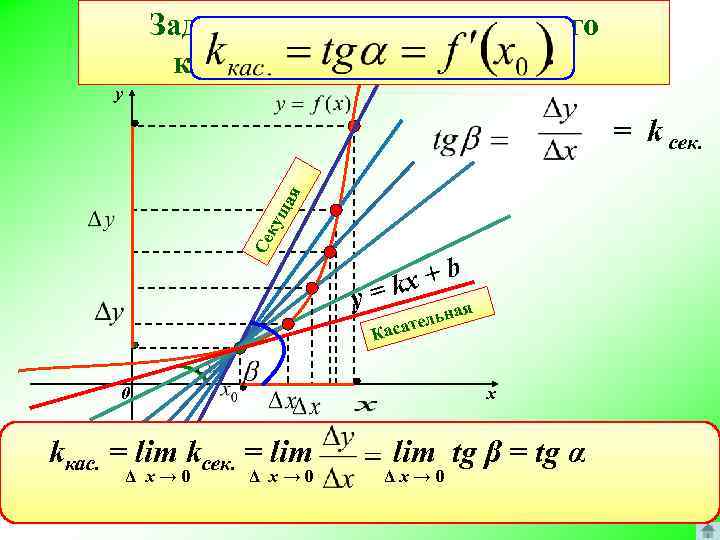Задача о нахождении углового коэффициента касательной y Се ку ща я = k сек. y x + b = k ая льн сате Ка 0 х kкас. = lim kсек. = lim tg β = tg α Секущая стремится занять положение касательной. Δ х → 0 То есть, касательная есть предельное положение секущей.

Уравнение касательной y = kx + b k = f / (x 0) y = f / (x 0) · x + b f(x 0) = f / (x 0) · x 0 + b b = f(x 0) − f / (x 0) · x 0 y = f / (x 0) · x + f(x 0) − f / (x 0) · x 0 y = f(x 0) + f / (x 0) · (x − x 0)

Итак: Уравнение касательной имеет вид: y = f(xo) + f '(xo)( x – xo)

Алгоритм • Найти значение функции в точке хо • Вычислить производную функции • Найти значение производной функции в точке хо • Подставить полученные числа в формулу y = f(xo) + f '(xo)( x – xo) • Привести уравнение к стандартному виду y = kx + b

Решение задачи. Составьте уравнение касательной к графику функции в точке M( 3; – 2). y = f(xo) + f '(xo)( x – xo)

Решение задачи. Написать уравнения всех касательных к графику функции у = х 3 − 3 х 2 + 3 параллельных прямой у = 9 х + 1 Решение. 1. Найдём х0. k = 9 = у'(х0 ). Ответ: Пусть х0 = а. 2. у'(х ) = 3 х 2 − 6 х; 3. у'(х0 ) = у'(a ) = 3 a 2 − 6 a; 4. 3 a 2 − 6 a = 9; a 2 − 2 a = 3; a 2 − 2 a − 3 = 0; a 1 = − 1; a 2 = 3. 5. х0 = − 1; х0 = 3. Дальше – по алгоритму.

Геометрический смысл производной. Производная функции в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.