Уравнение движения маятника (по II закону Ньютона) или

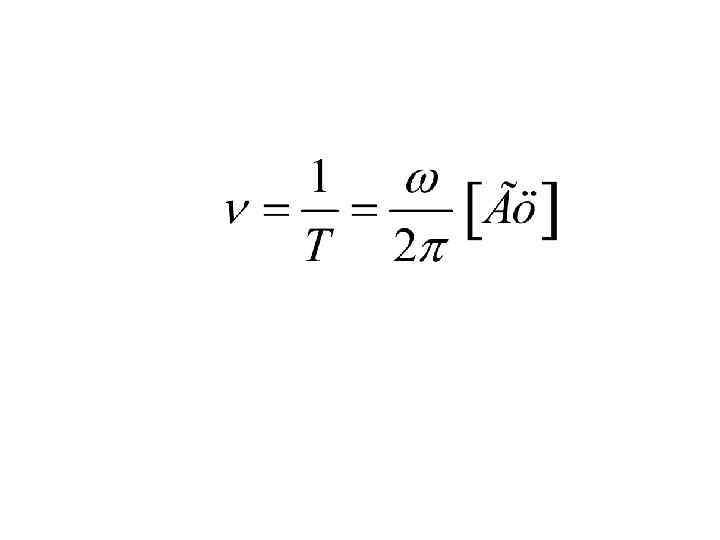
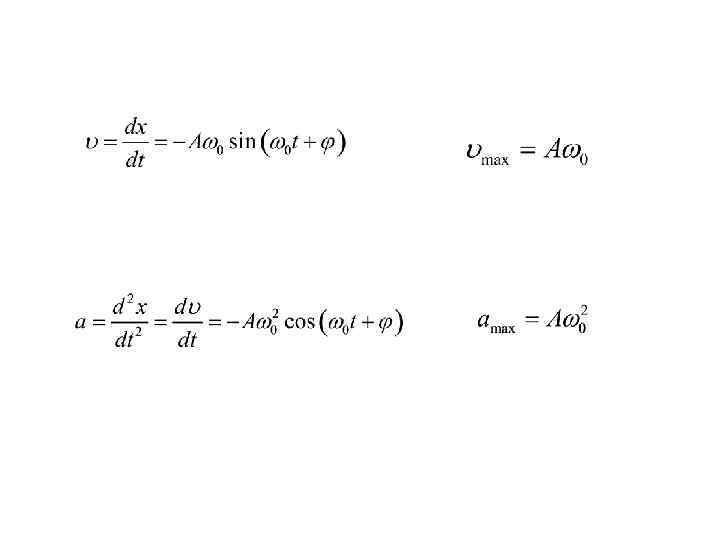
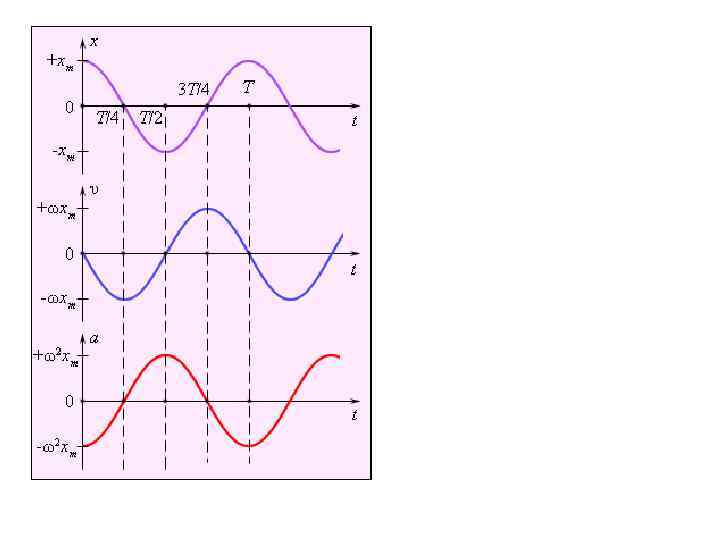
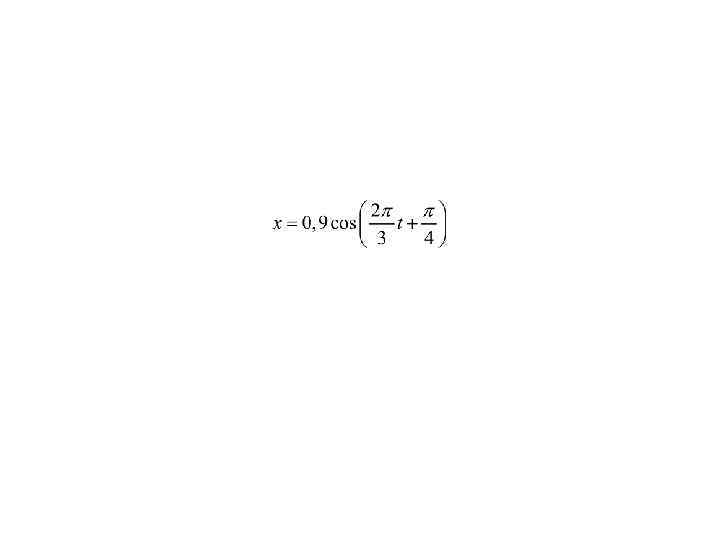
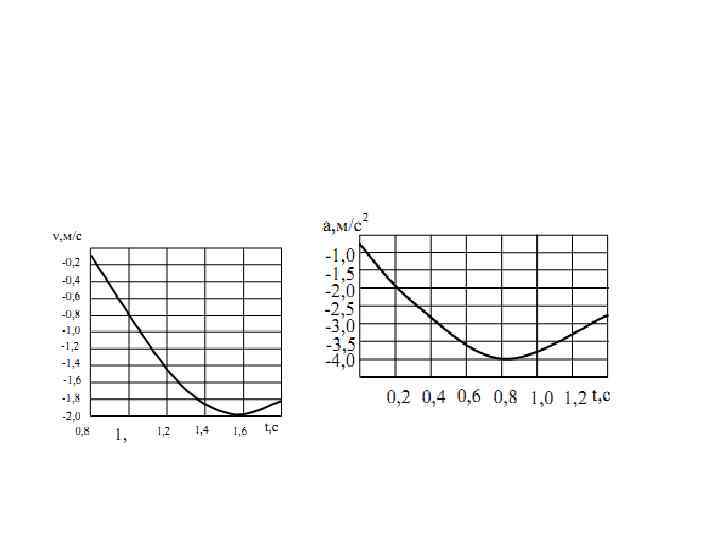
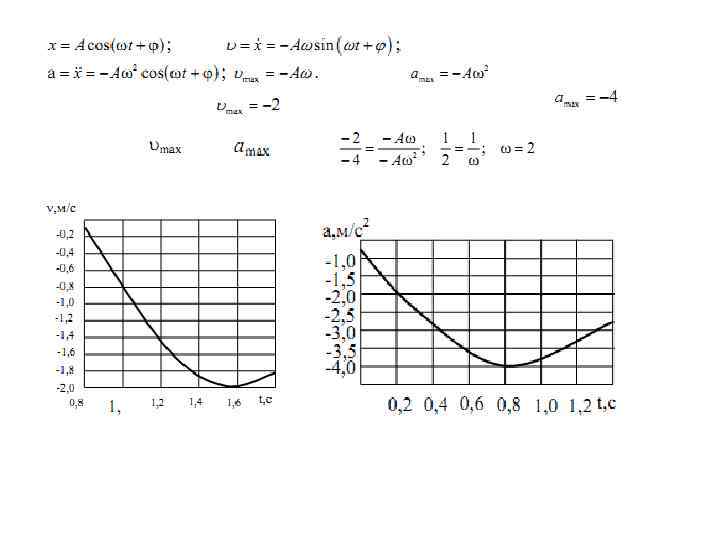
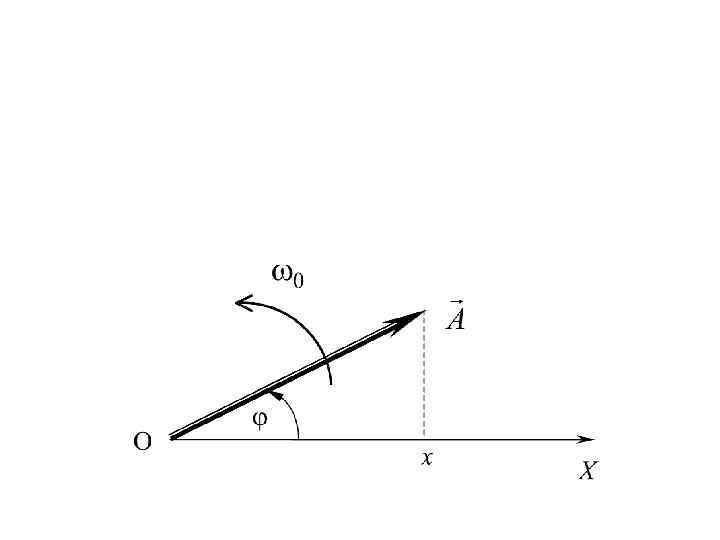
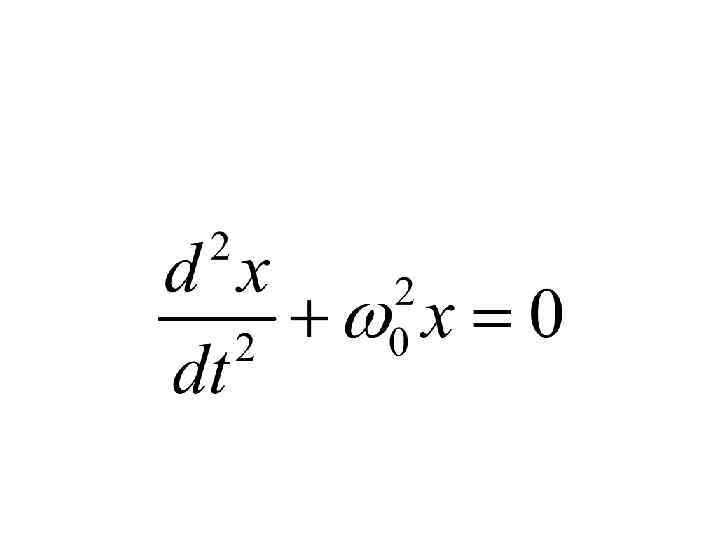
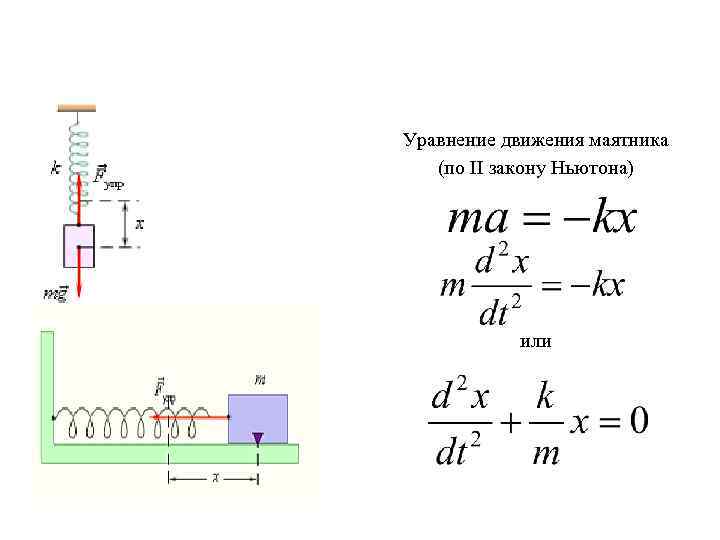Уравнение движения маятника (по II закону Ньютона) или

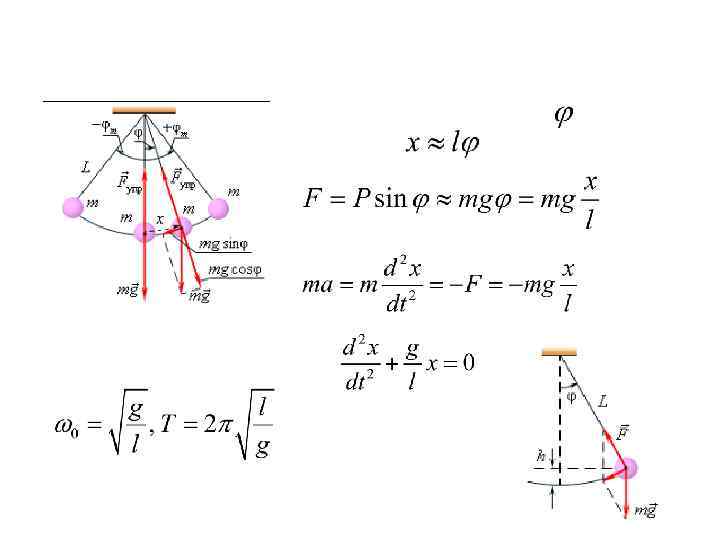
Сравним это уравнение с уравнением движения гармонического осциллятора. Получим значение циклической частоты и периода.

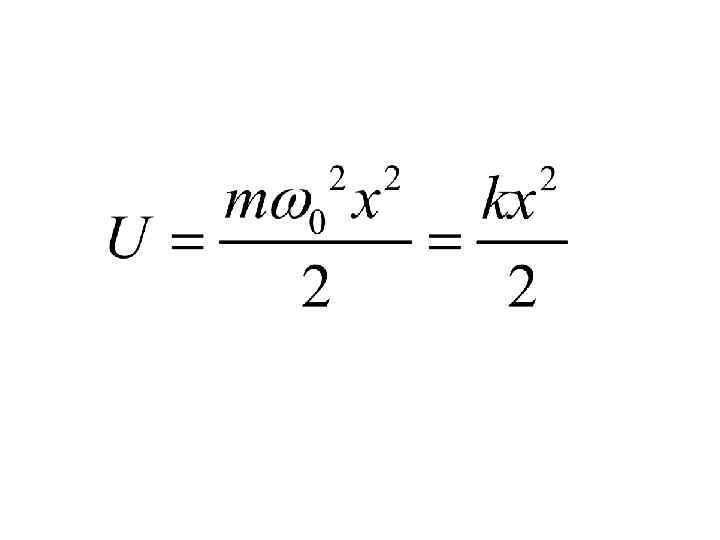
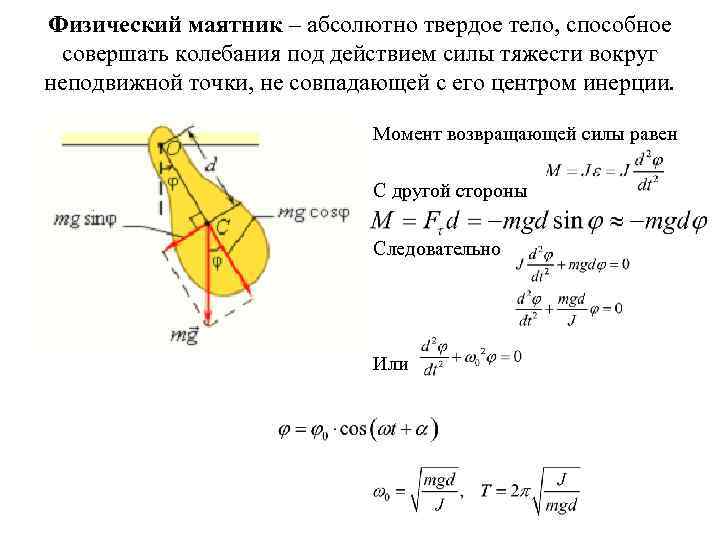Физический маятник – абсолютно твердое тело, способное совершать колебания под действием силы тяжести вокруг неподвижной точки, не совпадающей с его центром инерции. Момент возвращающей силы равен С другой стороны Следовательно Или

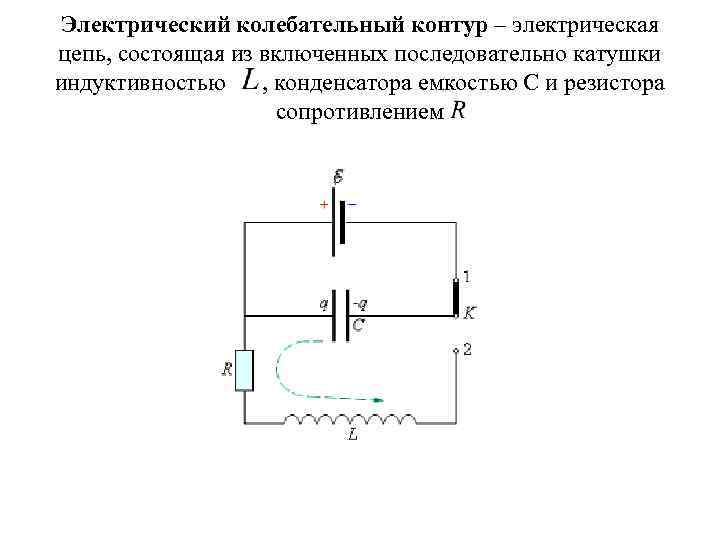Электрический колебательный контур – электрическая цепь, состоящая из включенных последовательно катушки индуктивностью , конденсатора емкостью С и резистора сопротивлением

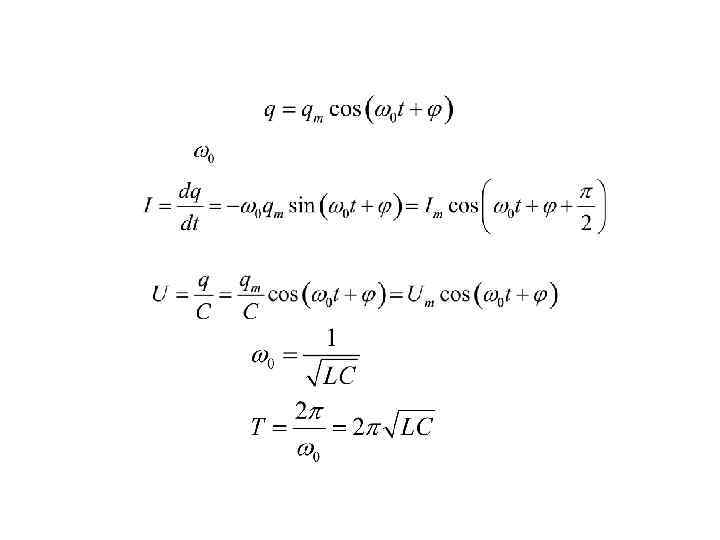
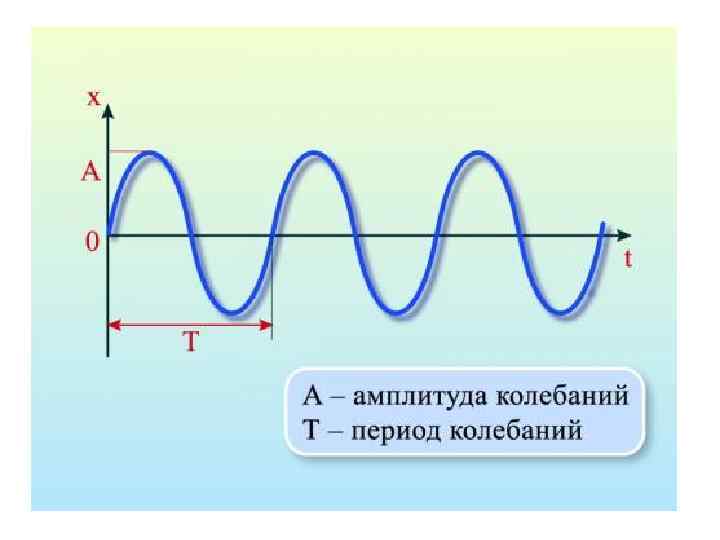
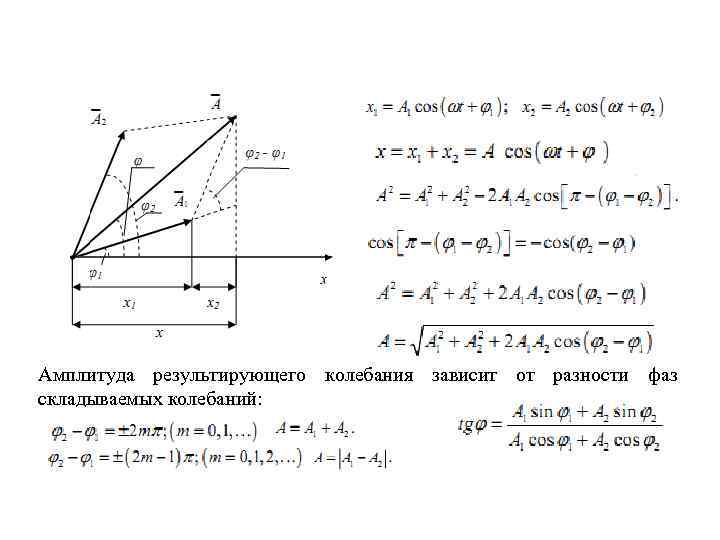Амплитуда результирующего колебания зависит от разности фаз складываемых колебаний:

РЕШЕНИЕ: Графически амплитуды складываемых колебаний можно изобразить так: Амплитуда результирующего колебания: Вычисления проводим по теореме косинусов: по условию тогда Ответ: .

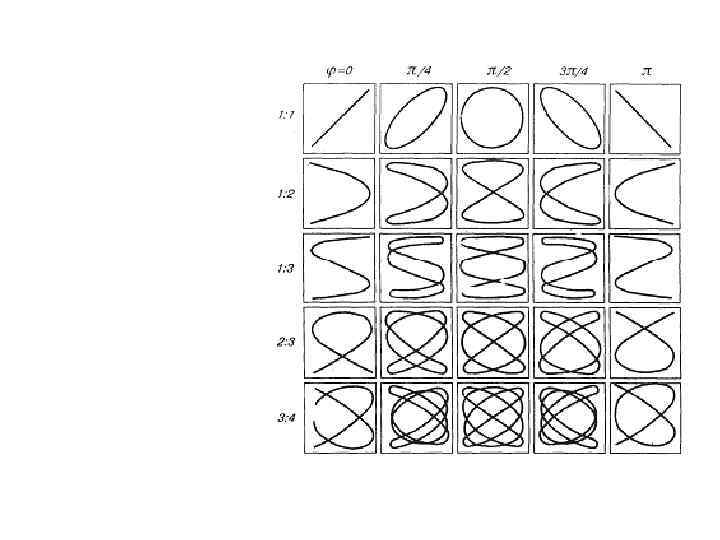
Сложение взаимно-перпендикулярных гармонических колебаний одинаковой частоты. Эллиптически поляризованные колебания Складываемые колебания Уравнение траектории результирующего колебания Это – уравнение эллипса. Эллиптически-поляризованные колебания – колебания, в которых траектория результирующего колебания имеет форму эллипса. Ориентация эллипса и его размеры зависят от амплитуд складываемых колебаний и разности фаз α.

Рассмотрим некоторые частные случаи, представляющие физический интерес: 1. Линейно поляризованные колебания

2. Циркулярно поляризованные колебания или колебания, поляризованные по кругу. Если разность фаз , то уравнение примет вид. Это уравнение эллипса, оси которого совпадают с осями координат, а его полуоси равны соответствующим амплитудам. Кроме того, если А=В, то эллипс вырождается в окружность.

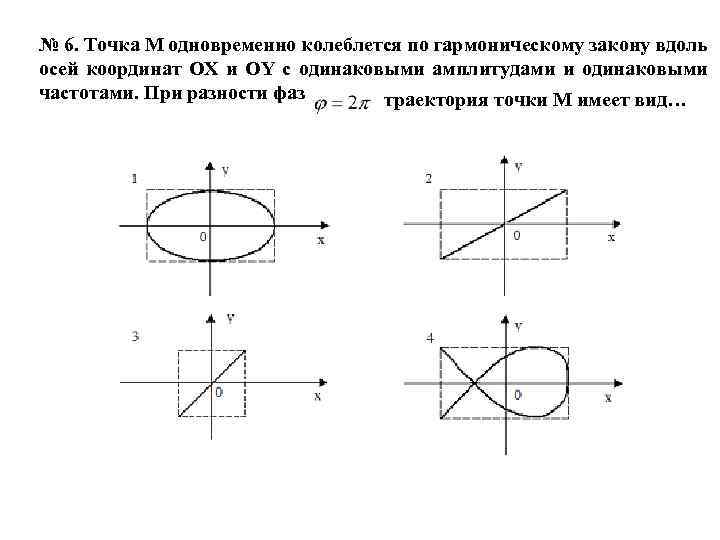№ 6. Точка М одновременно колеблется по гармоническому закону вдоль осей координат ОХ и OY с одинаковыми амплитудами и одинаковыми частотами. При разности фаз траектория точки М имеет вид…

- амплитуда затухающих колебаний - период затухающих колебаний

временя релаксации логарифмический декремент затухания добротность колебательной системы

Свободные затухающие колебания в электрическом колебательном контуре

Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся э. д. с. , называются соответственно вынужденными механическими и вынужденными электромагнитными колебаниями. В общем виде дифференциальное уравнение вынужденных колебаний имеет вид:

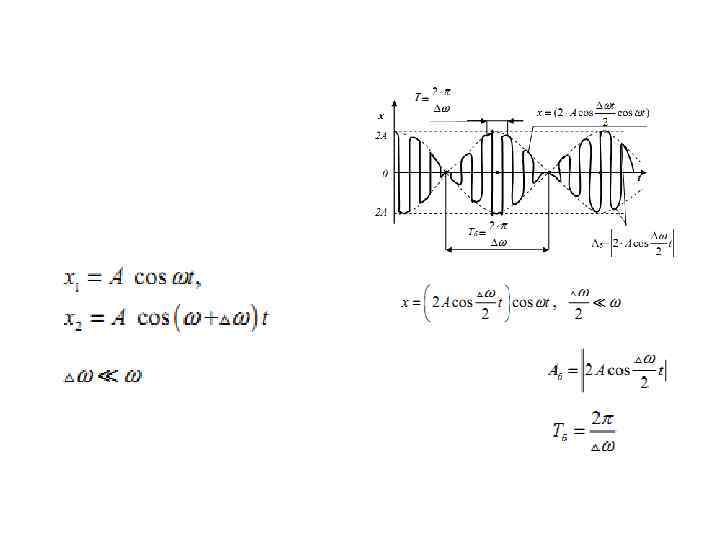
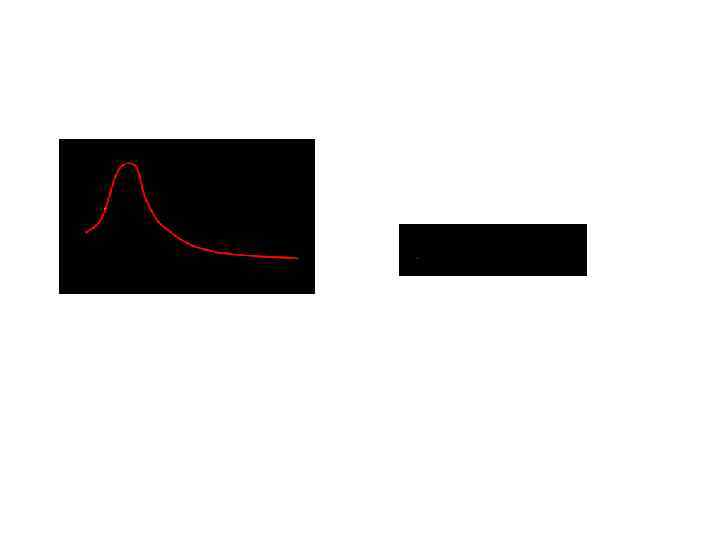
Процесс установления вынужденных незатухающих колебаний можно представить как процесс сложения двух колебаний: 1. затухающих колебаний 2. вынужденных колебаний

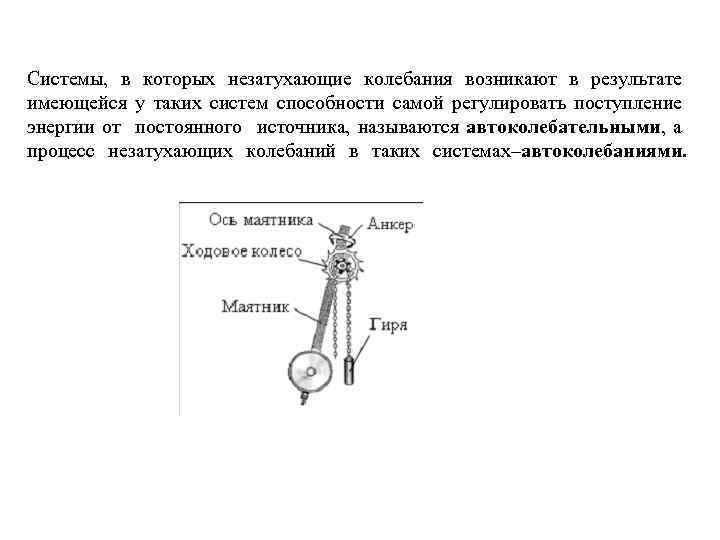Системы, в которых незатухающие колебания возникают в результате имеющейся у таких систем способности самой регулировать поступление энергии от постоянного источника, называются автоколебательными, а процесс незатухающих колебаний в таких системах–автоколебаниями.