УРАВНЕНИЕ ДИНАМИЧЕСКОГО РАВНОВЕСИЯ И ВОЛНОВОЕ УРАВНЕНИЕ СКАЛЯРНЫЙ И

УРАВНЕНИЕ ДИНАМИЧЕСКОГО РАВНОВЕСИЯ И ВОЛНОВОЕ УРАВНЕНИЕ. СКАЛЯРНЫЙ И ВЕКТОРНЫЙ ПОТЕНЦИАЛ

Уравнение динамического равновесия • Уравнения, получаемые из закона Ньютона, верны для изотропной среды (не обязательно однородной). • Результирующие силы на единицу объема по осям X, Y и Z можно выразить в виде • Полная сила в направлении X:

Уравнение динамического равновесия • Согласно второму закону Ньютона, несбалансированная сила равна массе на ускорение, т. е. уравнение движения по осям имеет вид: (1) Где И. т. д. (2)

Уравнение динамического равновесия • Если подставить выражение (2) в (1), то получим два уравнения динамического равновесия Ламе в векторной форме, которые верны для абсолютно упругих однородных изотропных сред: I. где ρ – плотность, λ и μ – постоянные Ламе, λ – коэффициент сжатия, μ – коэффициент сдвига, смещение частиц относительно положения равновесия, - изменение объема под действием нагрузок, внешние силы, под действием которой отдельные части тела движутся, возникают силы инерции.

Уравнение динамического равновесия • Т. к. , то подставив это выражение в первое уравнение движения, получим второй вариант написания уравнения: • II. - определяет изменение объема, – обусловлен неравномерным изменением объема, вследствие этого возникают упругие силы, если .

Понятие потенциалов. Волновые уравнения • Ввиду сложности уравнения Ламе, его упрощают. Вектор смещения определен в каждой точке среды и образует векторное поле смещений. Всякое векторное поле может быть представлено в виде суммы двух векторных полей – потенциального и вихревого (соленоидального) (разложение Гельмгольца)

Понятие потенциалов. Волновые уравнения • Потенциальное поле обладает скалярным потенциалом φ(x, y, z), а вихревое векторным потенциалом • Условие существования поля: • Аналогично, поле внешних возмущающих сил может быть представлено в виде суммы потенциальной и вихревой составляющих: Если в уравнение I подставить эти соотношения и опуская внешние силы:

Понятие потенциалов. Волновые уравнения • Применим к левой и правой частям уравнения операцию rot и обозначив Получим уравнение Лапласа Если среда безграничная, то функция гармоническая во всем пространстве и из этого следует равенство , и следует (векторное волновое уравнение).

Понятие потенциалов. Волновые уравнения • Подставим разложение Гельмгольца в уравнение II. Применим к обеим частям операцию div. Получаем волновое уравнение • При наличии внешних сил получим следующие уравнения для потенциалов поля Это неоднородные волновые уравнения

Понятие потенциалов. Волновые уравнения • Эти уравнения различаются только постоянными коэффициентами , и переменными величинами, кроме этого, второе уравнение является векторным и может быть представлено в виде совокупности трех скалярных уравнений. • Наличие независимых одно от другого уравнений указывает на существование в безграничной среде двух независимых возмущений. Одно из них - продольные волны P, другое – поперечные волны S.

Понятие потенциалов. Волновые уравнения • Каждому типу волн соответствуют определенные типы деформации. • Для P волн – это изменение элементарных объемов вещества – его сжатие и растяжение. Они описываются следующим выражением: как известно, • Для S-волн это малые повороты элементарных объемов. Они описываются вектором вращения т. к. в продольной волне повороты частиц отсутствуют, то При распространении волн эти деформации не зависят одна от другой, и каждая создает характерные движения.

Понятие потенциалов. Волновые уравнения • В области среды, где отсутствуют внешние источники (ξ 0, ), уравнения становятся однородными и принимают вид: (в однородной изотропной среде эти уравнения независимы) или

Понятие потенциалов. Волновые уравнения • Упругие процессы определяются тремя характеристиками: , и - независимыми параметрами. Для разных типов тел (сыпучих, кристаллических и пр. ) существует различная весьма сложная зависимость.

Понятие потенциалов. Волновые уравнения • В прямоугольных координатах

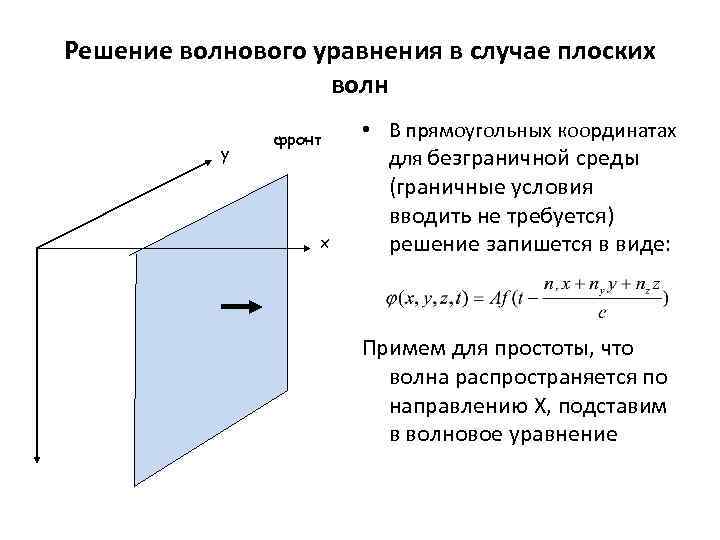Решение волнового уравнения в случае плоских волн y фронт x • В прямоугольных координатах для безграничной среды (граничные условия вводить не требуется) решение запишется в виде: Примем для простоты, что волна распространяется по направлению Х, подставим в волновое уравнение

Решение волнового уравнения в случае плоских волн • подставим решение в волновое уравнение • Учтем, что это выражение является решением волнового уравнения, если структура аргумента имеет вид где nx, ny, nz – направляющие косинусы нормали к поверхности волнового фронта.

Решение волнового уравнения в случае плоских волн Таким образом, любая функция с такой структурой и аргументом - 3 числа, являющиеся проекциями единичного вектора нормали к фронту волны на оси координат. является решением волнового уравнения. Будем считать, что некоторое возмущение распространяется как плоская волна в направлении l со скоростью c если: 1) в фиксированный момент времени эта величина неизменна в пространстве в каждой плоскости, нормальной к l , 2) плоскость, характеризуемая постоянным значением этой величины, перемещается со скоростью c в направлении l.

Решение волнового уравнения в случае плоских волн В другом виде можно записать - на такую величину будут отставать колебания в плоскости. Фронт такой волны - плоскость. В однородной изотропной среде возможно распространение плоской волны. Она представляет собой математическую абстракцию. Однако это понятие полезно, т. к. вдали от источника реальные волны, рассматриваемые в ограниченных областях пространства, по своим свойствам близки к плоским волнам. Поскольку изучение поведения плоских волн значительно проще сферических, многие задачи о распространении сферических волн решают, исходя из ее представления в виде совокупности плоских волн. Часто для упрощения полагают A равным 1.

Решение волнового уравнения в случае сферических волн • В сферических координатах волновое уравнение будет иметь вид где - коширота, т. е. дополнение до широты; - долгота. Для перевода в прямоугольные координаты можно использовать x=rsin cos , y=rsin , z=rcos. Напомним, что в выражении в числителе правой части стоит потенциал , а в знаменателе появляется долгота .

Решение волнового уравнения в случае сферических волн • Мы рассмотрим частный случай, когда характер волнового движения независим от потенциала и является функцией только r и t. Тогда мы получим упрощенный вид уравнения: • Это уравнение имеет решение для потенциала • Очевидно, что также является решением выражение для потенциала общее решение примет вид • • Первый член соответствует волне, которая распространяется наружу от центральной точки, а второй – волне, которая идет по направлению к этой центральной точке. Если r и t имеют фиксированные значения, то Vt и, следовательно, , постоянны. Таким образом, в момент времени t во всех точках на сферической поверхности радиуса r волна характеризуется одним и тем же значением.

Смещение для продольных волн Рассмотрим смещение для продольных волн Выберем координатные оси так, чтобы присутствовали компоненты смещения X, Z, а Y-компонента отсутствовала Решение волнового уравнения: Учтем, что Где Итак, в продольной волне смещение частиц идет вдоль одной линии, т. е. мы можем ввести понятие о линейно-поляризованных волнах. Смещение частиц идет по нормали к поверхности волнового фронта. Волны, для которых смещение идет вдоль одной линии, называются линейно-поляризованными.

Смещение поперечных волн. Поперечные волны горизонтальной и вертикальной поляризации Рассмотрим поперечные волны. Рассмотрим смещение S волн, . Для них волновое уравнение – векторное, распадается на три скалярных уравнения. Запишем смещение поперечных волн:

Смещение поперечных волн. Поперечные волны горизонтальной и вертикальной поляризации Поперечные волны можно Из ограничения для разделить на два типа: потенциала =0 следует, 1. SV - волны что вертикальной поляризации. Волны вертикальной поляризации (SV волны). Смещение таких волн происходит в вертикальной плоскости, и имеет компоненты X и Z: исходя из определения. Если волна поляризована только как SV, то Y – компонента смещения равна нулю и

Смещение поперечных волн. Поперечные волны горизонтальной и вертикальной поляризации В контексте ТФКП, эти оба уравнения являются уравнениями Коши-Римана, и из этого следует, что функция ψz+i ψx – аналитическая функция переменной x+iz. Функция, которая iz повсюду аналитична и ограничена является константой (согласно теореме Лиувилля). Для плоской волны ψz+iψx – ограничена, более того, если SV волна задается потенциалом rot только в ограниченном диапазоне глубин, то можно распространить это смещение на все глубины, так, что функция ψz+iψx будет аналитична повсюду. Из этого следует, что ψz+iψx – константа. Поскольку физический смысл имеют только градиенты, то константу можно принять за ноль. Получаем Таким образом векторный потенциал задается только одной компонентой и равны нулю.

Смещение поперечных волн. Поперечные волны горизонтальной и вертикальной поляризации Полное смещение для вертикально поляризованных волн запишется в виде:

Смещение поперечных волн. Поперечные волны горизонтальной и вертикальной поляризации 2. SH – волны горизонтальной поляризации. Смещения поляризации таких волн имеют только Y компоненту. В свою очередь, векторный потенциал имеет две компоненты, X и Z. Для плоской SH волны использование векторного потенциала не требуется, т. к. компонента горизонтального смещения сама является скалярной функцией, с которой можно работать. Запишем два волновых уравнения, найдем производные по z и по x, соответственно и вычтем одно из другого.

Смещение поперечных волн. Поперечные волны горизонтальной и вертикальной поляризации найдем производную от и вычтем из нее производную получим Т. е. от Имеем: волновое уравнение для SH волн выполняется для самих смещений

Волновое уравнение для жидкостей и газов В случае жидкой или газообразной среды волновое уравнение для потенциалов переходит в волновое уравнение для давления: Покажем это следующим образом: т. к. напряжение нормально площадке исходное волновое уравнение Таким образом, как мы и хотели доказать, волновое уравнение в случае жидкостей и газов выполняется для давления:

• Что такое уравнение динамического равновесия Ламе? • Что такое волновое уравнение? • Как записывается решение волнового уравнения в случае плоских волн? • Как записывается решение волнового уравнения в случае сферических волн? • Что такое SH и SV волны?