Уравнение Бернулли для потока реальной вязкой жидкости 1

Уравнение Бернулли для потока реальной (вязкой) жидкости (1. 57)

При переходе от элементарной струйки идеальной Ж к потоку реальной (вязкой) Ж, имеющему конечные размеры и ограниченному стенками, необходимо учесть неравномерность скоростей по сечению и потери энергии (напора), что является следствием вязкости жидкости.

При движении вязкой Ж вдоль твердой стенки (в трубе) происходит торможение потока вследствие влияния вязкости, а также из-за действия сил молекулярного сцепления между Ж и стенкой. Поэтому наибольшего значения скорость достигает в центральной части потока, а по мере приближения к стенке она уменьшается практически до нуля. Получается распределение скоростей подобное показанному на рис.

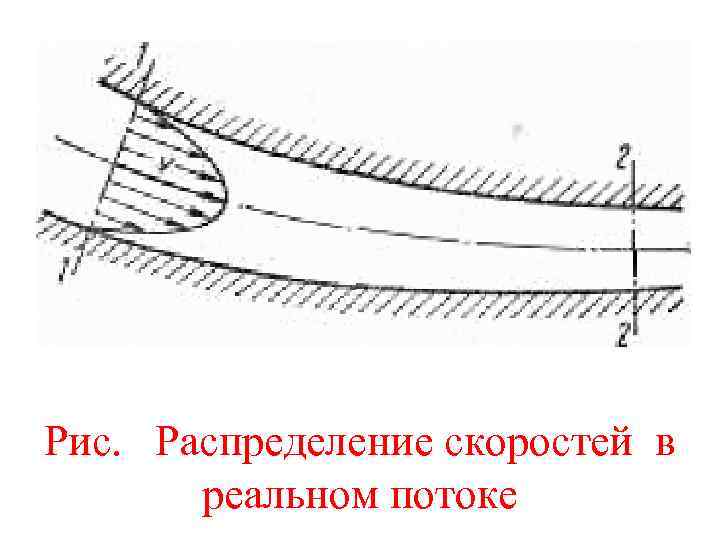
Рис. Распределение скоростей в реальном потоке

Неравномерное распределение скоростей означает скольжение (сдвиг) одних слоев или частей Ж по другим, вследствие чего возникают касательные напряжения (напряжения трения). Движение вязкой Ж часто сопровождается вращением частиц, вихреобразованием и перемешиванием.

На все это затрачивается энергия, поэтому удельная энергия движущейся вязкой Ж не остается постоянной, как в идеальной Ж, а постепенно расходуется на преодоление сопротивлений, поэтому уменьшается вдоль потока. Из-за неравномерного распределения скоростей в рассмотрение вводятся средние по сечению скорость υср, и значение удельной энергии жидкости в данном сечении.

Сделаем допущение: считаем, что в пределах рассматриваемых поперечных сечений потока справедлив основной закон гидростатики (гидростатический напор в пределах сечения есть величина, одинаковая для всех точек данного сечения: z + p/(ρg) = const, т. е. предполагаем, что при движении жидкости отдельные струйки оказывают одна на другую в поперечном направлении такое же давление, как и в неподвижном состоянии). Это может быть доказано теоретически в том случае, когда течение в данных поперечных сечениях является параллельноструйным. Именно такие (или близкие

в данном сечении: это полная энергия, которую проносит поток через это сечение в единицу времени. Так как в различных точках поперечного сечения потока частицы Ж обладают различной энергией, выразим сначала мощность элементарной струйки в виде произведения полной удельной энергии Ж в данной точке на элементарный массовый расход: d. N = g. H d. Qm=(gz + p/ρ+υ2/2)ρυ d. S.

Мощность всего потока найдется как интеграл от предыдущего выражения по всей площади S: или, учитывая сделанное допущение (z + p/(ρg) = =const),

Найдем среднее по сечению значение полной удельной энергии жидкости делением полной мощности потока на массовый расход. Используя выражение (1. 41 ), получаем Умножив и разделив последний член на получим (переходя к напорам) (1. 55) ,

где — безразмерный коэффициент Кориолиса, учитывающий неравномерность распределения скоростей: (1. 56) Если умножить числитель и знаменатель (1. 56) на ρ/2, то нетрудно убедиться, что коэффициент представляет собой отношение действительной кинетической энергии потока в данном сечении к кинетической энергии того же потока и в том же сечении, но при равномерном распределении скоростей.

Для обычного распределения скоростей (рис. ) > 1, а при равномерном распределении скоростей = 1. Возьмем два сечения реального потока и обозначим средние значения полного напора жидкости в этих сечениях соответственно Нср1 и Нср2, Тогда где hп - суммарная потеря полного напора на участке между рассматриваемыми сечениями. С использованием этой формулы для Нср, предыдущее уравнение (1. 55) перепишется так:

(1. 57) Это и есть уравнение Бернулли для потока вязкой жидкости. От аналогичного уравнения (1. 49 по форме записи) для элементарной струйки идеальной жидкости уравнение отличается членом, представляющим собой потерю полного напора, и коэффициентом α, учитывающим неравномерность распределения скоростей. Кроме того, скорости, входящие в это уравнение, являются средними по сечениям.

Умножение уравнения (1. 57) на g дает форму записи уравнения Бернулли для потока вязкой жидкости, соответствующую формуле (1. 50), где члены выражают виды энергии, отнесенной к единице массы, а член g hп представляет собой потерю удельной энергии жидкости. Умножение уравнения (1. 57) на ρg дает третью форму записи уравнения Бернулли для потока вязкой жидкости, соответствующую формуле (1. 51), но член ρg hп выражает потерю энергии, отнесенную к единице объема жидкости. Уравнение Бернулли (1. 57) и его формы применимы не только для жидкостей, но и для газов при условии, что скорость их движения значительно меньше скорости звука.

Графически это уравнение можно представить диаграммой, как для идеальной жидкости, но с учетом потерь напора, которые являются некоторой высотой, неуклонно возрастающей вдоль потока. Для струйки идеальной жидкости уравнение Бернулли представляет собой закон сохранения механической энергии, а для потока реальной жидкости оно является уравнением баланса энергии с учетом потерь.

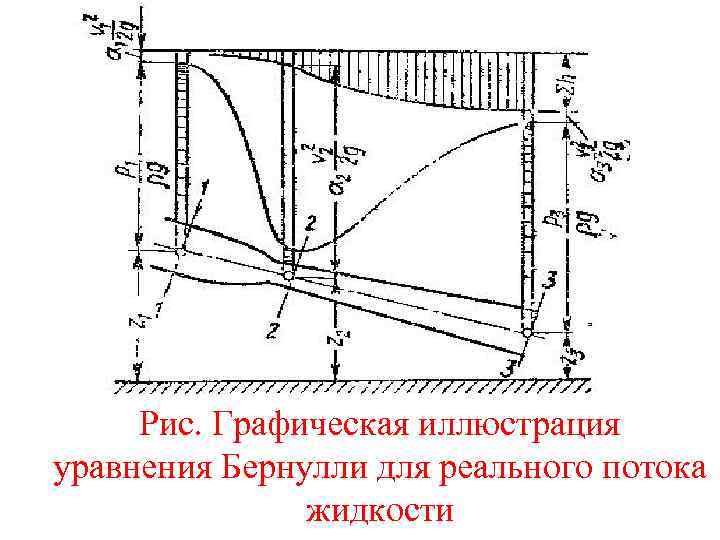
Рис. Графическая иллюстрация уравнения Бернулли для реального потока жидкости

Энергия, теряемая жидкостью на участке течения не исчезает бесследно, а превращается в другую форму тепловую. Ввиду того, что удельная теплоемкость жидкостей велика по сравнению с потерями удельной энергии, а тепловая энергия непрерывно рассеивается, повышение температуры часто бывает практически незаметным. Этот процесс преобразования механической энергии в тепловую является необратимым, т. е. таким, обратное течение которого (превращение тепловой энергии в механическую) невозможно.

Гидравлическим уклоном называется уменьшение среднего значения полной удельной энергии жидкости вдоль потока, отнесенное к единице его длины. Пьезометрическим уклоном называется изменение удельной потенциальной энергии жидкости, отнесенное к единице длины. В трубе постоянного диаметра с неизменным распределением скоростей указанные уклоны одинаковы.

Гидравлические потери (общие сведения) Потери удельной энергии (напора), или, гидравлические потери, зависят от формы, размеров русла, скорости течения и вязкости жидкости, а иногда и от абсолютного давления в ней. Вязкость жидкости является первопричиной всех потерь, но далеко не всегда оказывает существенное влияние на их величину.

Как показывают опыты, часто гидравлические потери ~ пропорциональны скорости течения жидкости в квадрате, поэтому в гидравлике принят общий способ выражения гидравлических потерь полного напора в линейных единицах: (1. 58) или в единицах давления

Это удобно тем, что включает в себя безразмерный коэффициент ζ, называемый коэффициентом потерь (коэффициентом сопротивления), значение которого для данного русла в первом приближении принимают постоянным. Коэффициент потерь ζ - это отношение потерянного напора к скоростному напору. Гидравлические потери обычно разделяют на местные потери и

Местные потери энергии обусловлены местными гидравлическими сопротивлениями, т. е. местными изменениями формы и размера русла, вызывающими деформацию потока. При протекании жидкости через местные сопротивления изменяется ее скорость и обычно возникают крупные вихри (образуются за местом отрыва потока от стенок и представляют собой области, в которых частицы жидкости движутся в основном по замкнутым кривым или близким к ним траекториям). 06 11 08

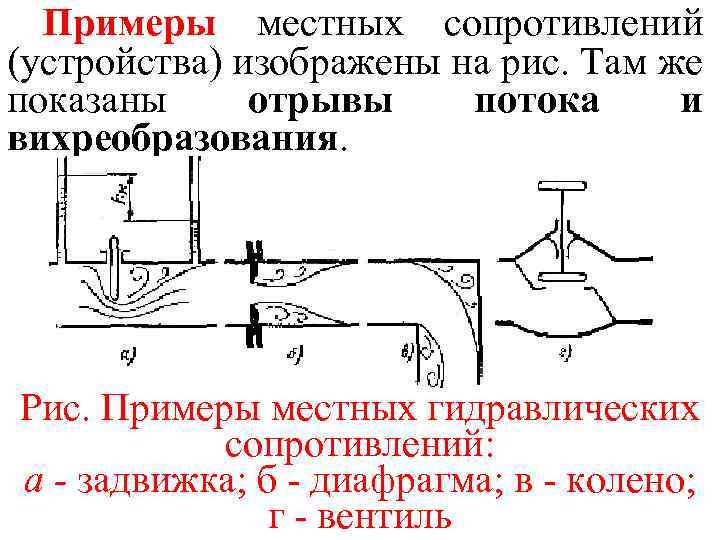
Примеры местных сопротивлений (устройства) изображены на рис. Там же показаны отрывы потока и вихреобразования. Рис. Примеры местных гидравлических сопротивлений: а - задвижка; б - диафрагма; в - колено; г - вентиль

Местные потери напора определяются по формуле (1. 58) следующим образом: (1. 59) или в единицах давления Выражение (1. 59) называют формулой Вейсбаха. В ней υ средняя по сечению скорость в трубе, в которой установлено местное сопротивление.

Если же диаметр трубы, а значит и скорость в ней изменяются по длине, то за расчетную скорость удобнее принимать большую из скоростей (в меньшем диаметре трубы). Каждое местное сопротивление характеризуется своим значением ζ, которое во многих случаях приближенно можно считать постоянным для данной формы местного сопротивления. 30 11 09 стэ 31

Потери на трение по длине, — это потери энергии, которые возникают в прямых трубах постоянного сечения, т. е. при равномерном течении, и возрастают пропорционально длине трубы (рис. ). Рассматриваемые потери обусловлены внутренним трением в жидкости, а потому имеют место не только в шероховатых, но и в гладких трубах. Рис. Потери на трение по длине трубы

Потерю напора на трение можно выразить по общей формуле (1. 58) для гидравлических потерь, т. е. (1. 60) однако удобнее коэффициент ζ связать с относительной длиной трубы l/d. Возьмем участок круглой трубы длиной, равной ее диаметру, и обозначим его коэффициент потерь, входящий в формулу (1. 60), через . Тогда для всей трубы длиной l и диаметром d коэффициент потерь будет в l/d раз больше:

В результате формула (1. 60) примет вид (1. 61) или в единицах давления (1. 62) Формулу (1. 61) обычно называют формулой Вейсбаха — Дарси. Эти формулы для основных режимов течения жидкости можно получить теоретически.

Безразмерный коэффициент называют коэффициентом потерь на трение по длине, или коэффициентом Дарси. Его можно рассматривать как коэффициент пропорциональности между потерей напора на трение, и произведением относительной длины трубы на скоростной напор. Физический смысл коэффициента можно выяснить, если рассмотреть условие равномерного движения в трубе цилиндрического объема длиной l и диаметром d (см. рис. ), т. е. равенство нулю суммы сил, действующих на объем: сил давления и силы трения. Это равенство имеет вид где 0 — напряжение трения на стенке трубы.

Если учесть формулу (1. 62), то легко получить (1. 63) т. е. коэффициент есть величина, пропорциональная отношению напряжения трения на стенке трубы к динамическому давлению, определенному по средней скорости. Ввиду постоянства объемного расхода несжимаемой жидкости вдоль трубы постоянного сечения скорость и удельная кинетическая энергия также остаются постоянными, несмотря на наличие гидравлических сопротивлений и потерь напора. Потери напора в этом случае определяются разностью показаний двух пьезометров (см. предыдущие рис. ).

Уравнение Бернулли для относительного движения (1. 64)

Уравнение Бернулли (формулы 1. 49 и 1. 57) справедливо для установившегося течения, когда из массовых сил на жидкость действует лишь сила тяжести. В некоторых течениях кроме силы тяжести следует учитывать силы инерции переносного движения (например, когда русло с движущейся жидкостью, перемещается в пространстве с ускорением).

Если инерционная сила постоянна по времени, то течение жидкости относительно стенок м. быть установившимся, и для него можно вывести уравнение Бернулли так же, как это делали ранее. Различие заключается в том, что в левую часть уравнения (1. 48') к работе сил давления и тяжести следует добавить работу силы инерции, действующую на элемент струйки весом d. G при его перемещении из сечения 1 -1 в сечение 2 -2 (см. рис. ). Эту работу, как и другие члены уравнения (1. 48') делим на d. G, т. е. относим к единице веса, и, получив некоторый напор, переносим

Получим уравнение Бернулли для относительного движения, которое в случае реального потока принимает вид (1. 64) где Нин - инерционный напор - представляет собой работу силы инерции, отнесенную к единице веса и взятую с обратным знаком (обратный знак обусловлен тем, что эта работа перенесена из левой части уравнения в правую).

Рассмотрим определение Нин для двух основных случаев относительного движения Ж. 1. Прямолинейное равноускоренное движение русла. Если русло, по которому течет Ж, движется прямолинейно с постоянным ускорением а (рис. а), то на все частицы Ж действует одинаковая и постоянная по времени сила инерции переносного движения, которая может способствовать или препятствовать

Рис. Схема для вывода уравнения Бернулли для относительного движения

силу отнести к единице массы, то она будет Если равна эту соответствующему ускорению а и направлена в сторону, обратную ему, а на каждую единицу веса жидкости будет действовать сила инерции a/g.

Работа этой силы при перемещении жидкости из сечения 1 -1 в сечение 22 (так же, как и работа силы тяжести) не зависит от формы пути, а определяется лишь разностью координат, отсчитываемых в направлении ускорения а, следовательно, Hин = ala/g, (1. 65) где 1 а - проекция рассматриваемого участка русла на направление ускорения а.

Знак, с которым величина Hин записывается в правой части уравнения Бернулли определяется правилом, вытекающим из физики явления. Если ускорение а направлено от сечения 1 -1 к сечению 2 -2, а сила инерции - наоборот, то эта сила препятствует течению жидкости, и инерционный напор имеет знак «+» (он уменьшает напор в сечении 2 -2 по сравнению с напором в сечении 1 -1 и аналогичен гидравлическим потерям hп, которые всегда входят в правую часть уравнения Бернулли со знаком «+» ).

Если же ускорение а направлено от сечения 2 -2 к сечению 1 -1, то сила инерции способствует течению и инерционный напор имеет знак «-» (инерционный напор увеличивает напор в сечения 2 -2, т. е. будет как бы уменьшать гидравлические потери).

2. Вращение русла вокруг вертикальной оси. Пусть русло, по которому движется Ж, вращается вокруг вертикальной оси с постоянной угловой скоростью (рис. б). Тогда на Ж действует сила инерции вращательного движения, являющаяся функцией радиуса. 10 11 08 Рис. б.

На единицу веса будет действовать сила инерции 2 r/g. Работа этой силы при перемещении вдоль радиуса на расстояние dr равна 2 rdr/g, а при перемещении от радиуса r 1 до радиуса r 2 (по любой кривой) работа найдется интегрированием этого выражения в пределах от r до r.

Выполнив интегрирование, найдем инерционный напор, только знак следует изменить на обратный (как указывалось выше): (1. 66) Знак инерционного напора, который получается при подсчете по этой формуле, соответствует указанному выше правилу знаков.