++НЕЧЕТКИЕ МНОЖЕСТВА 19112014.pptx
- Количество слайдов: 89

Уральский федеральный университет Институт фундаментального образования Кафедра Информационных систем и технологий Потанин Н. И. Лекция НЕЧЕТКИЕ МНОЖЕСТВА Екатеринбург, 2012

цель изучения материала . Перечень компетенций, формирующихся или получающих приращение в процессе знакомства с материалом.

СОДЕРЖАНИЕ 1. Нечеткие множества, история, основные операции, построение нечетких множеств.

Парадокс лысого • Человек, у которого на голове нет ни одного волоса — лыс. • Если у лысого вырастет еще один волосок, он останется лысым. • Значит, все люди лысые.

Парадокс кучи 1. Парадокс кучи Одно зерно – не куча. Добавим еще одно зерно – не куча и т. д. Вывод : кучи не существует. 1. Парадокс бороды (лысого) Разрешился с помощью нечетких множеств

История


Теорема о нечеткой аппроксимации

Следствие Коко • Любую практическую задачу можно решить с помощью нечетких множеств




• Как решить парадоксы кучи, бороды с помощью нечеткого множества?

Функции Принадлежности
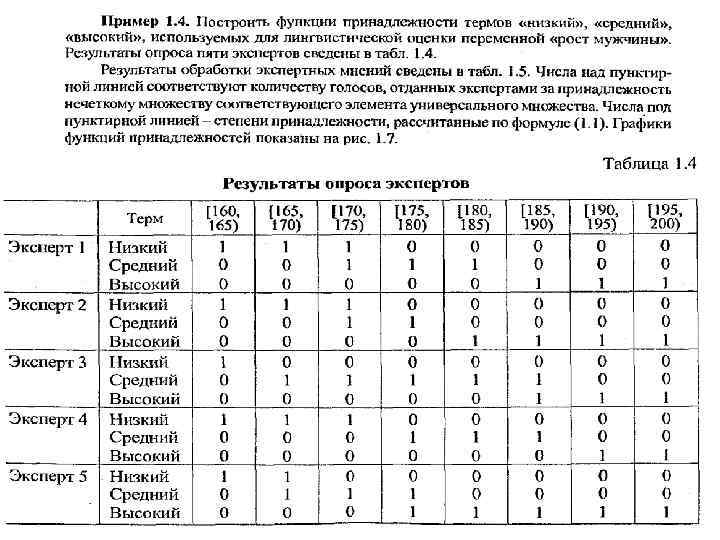
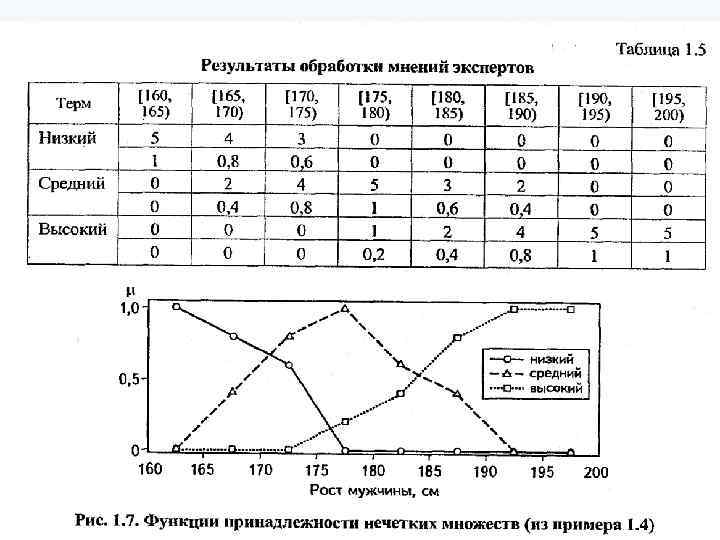


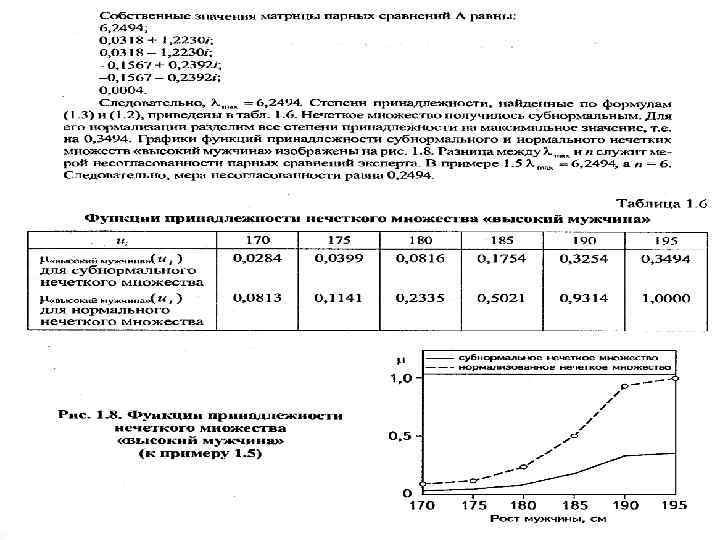
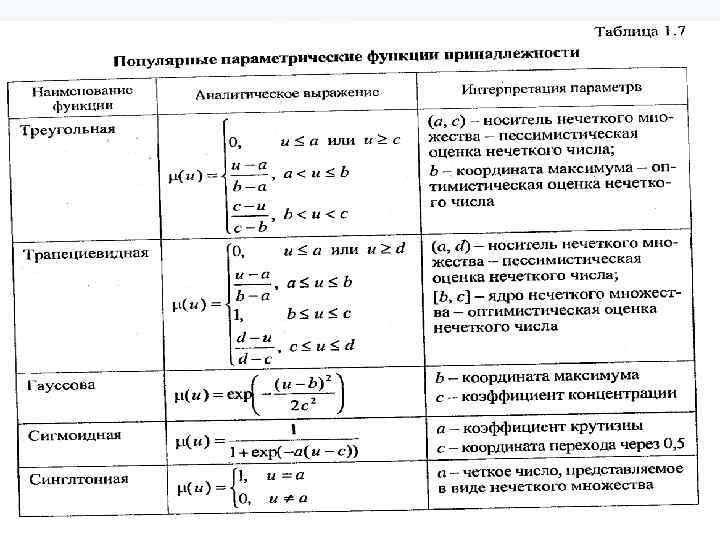


СВОЙСТВА НЕЧЕТКИХ МНОЖЕСТВ
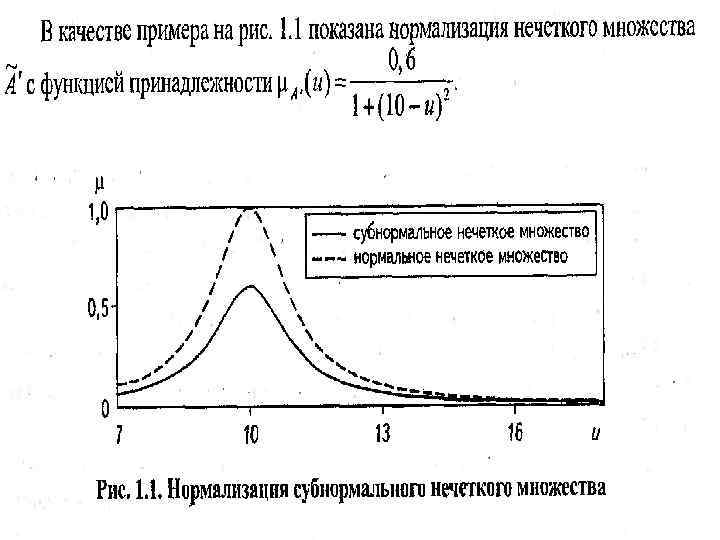

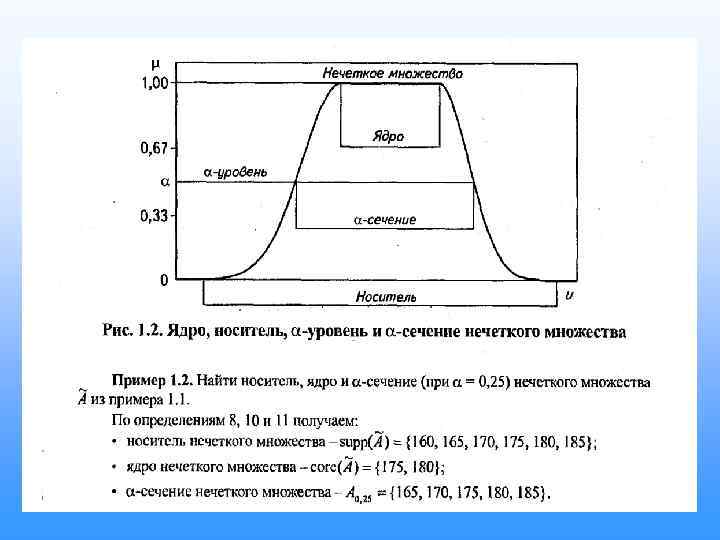

• Выпуклая область если через 2 любых точек из области провести отрезок, то все точки отрезка принадлежат области
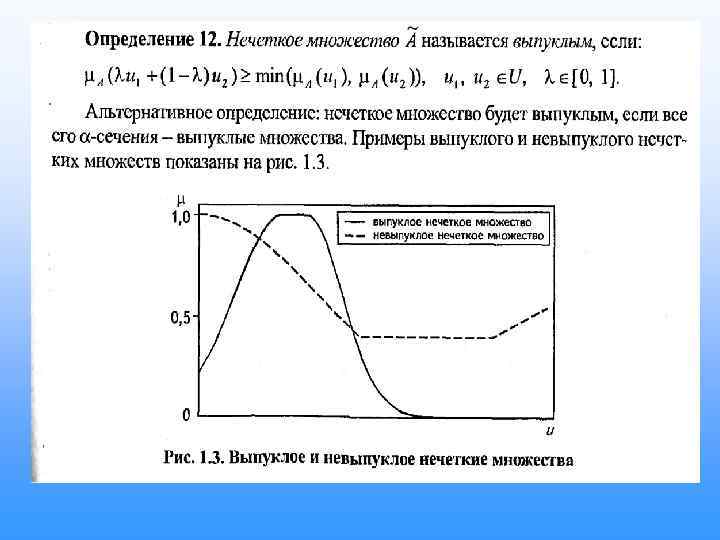

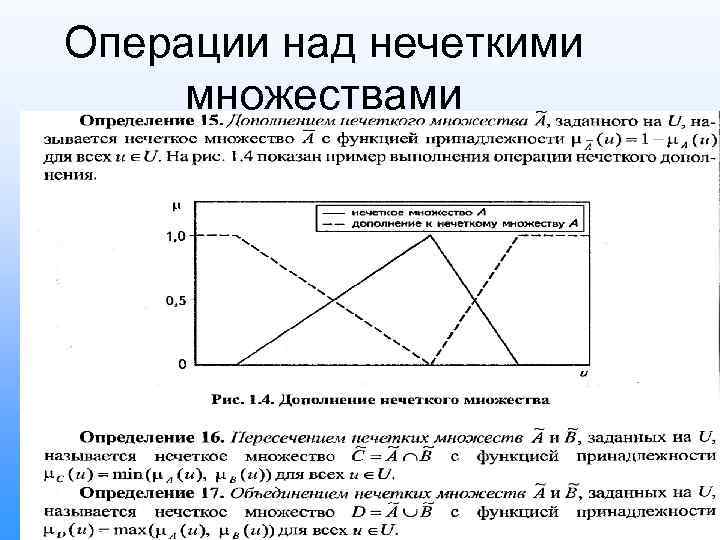
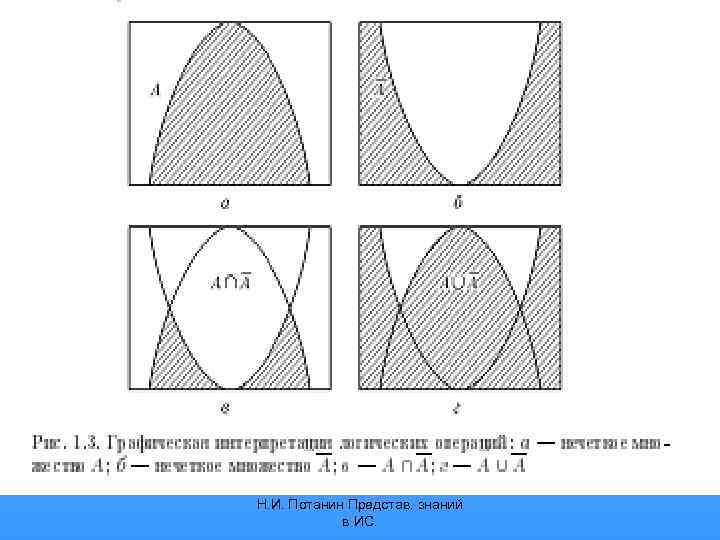
Операции над нечеткими множествами

Н. И. Потанин Представ. знаний в ИС.
Н. И. Потанин Представ. знаний в ИС.




Н. И. Потанин Представ. знаний в ИС.

Нечеткое множество "небольшое натуральное число" Например, возьмем в качестве универсума X={1, 2, 3, . . . } — множество натуральных чисел. Тогда нечеткое множество А, представляющее в некотором контексте "небольшое натуральное число", можно задать следующим образом: A={<1, 1. 0>, <2, 1. 0>, <3, 0. 9>, <4, 0. 8>, <5, 0. 6>, <6, 0. 5>, <7, 0. 4>, <8, 0. 2>, <9, 0. 1 >}. При этом элементы, для которых функция принадлежности равна нулю, отсутствуют в этом списке.

Нечеткое множество «Выходные дни» Обычное множество выходных дней А состоит из двух элементов: А = {суббота, воскресенье}. В определении соответствующего нечеткого множества A попытаемся субъективно оценить степень нашего эмоционального отношения к различным дням недели, рассматривая их с точки зрения выходных и психологии возможного отдыха: A={<понедельник, 0>, <вторник, 0>, <среда, 0>, <четверг, 0>, <пятница, 0. 5>, <суббота, 1. 0>, <воскресенье, 0. 8>}. Здесь в качестве универсума выступают все дни недели Х={понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}.

Графическое представление нечеткого множества Представим это нечеткое множество графически: изобразим графически функцию принадлежности этого нечеткого множества. Для этого на горизонтальной ос отметим отдельные значения элементов универсума (в нашем случае — элементы множества X), а на вертикальной оси — значения соответствующей функции принадлежности.
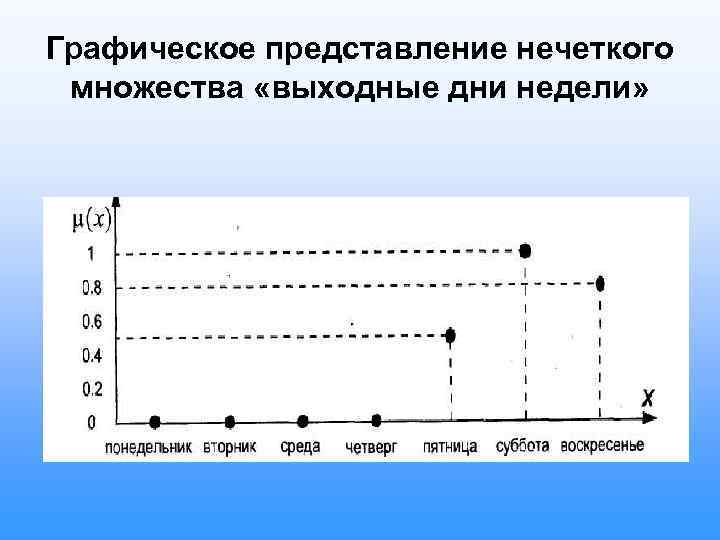
Графическое представление нечеткого множества «выходные дни недели»

Неоднозначность определения понятия нечетким множеством Оценка понятия «выходных дней» в высшей степени субъективна. В качестве нечеткого множества A также вполне могли бы выступать множества: А={<понедельник, 0>, <вторник, 0>, <среда, 0>, <четверг, 0. 1>, <пятница, 0. 6>, <суббота, 1. 0>, <воскресенье, 0. 7>} A={<понедельник, 0>, <вторник, 0>, <среда, 0>, <четверг, 0. 1 >, <пятница, 0. 5>, <суббота, 0. 9>, <воскресенье, 0. 8>}.
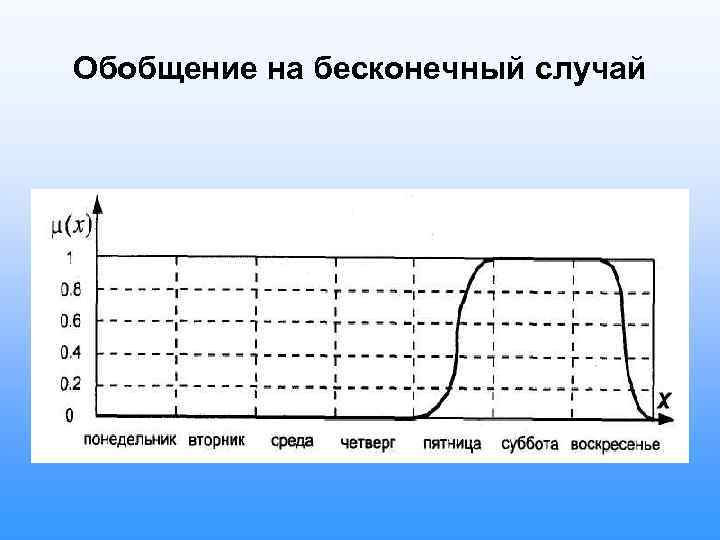
Обобщение на бесконечный случай

Нечеткое множество "горячий кофе". Универсум: Х={х | 0 °С <х< 100 °С}. Для остальных значений температуры между 20 и 80 градусами нет и не может быть единого мнения, горячий или нет напиток. Тем не менее, есть свойства функции принадлежности, с которыми согласны все, т. е. которые в какой-то степени можно считать объективными.
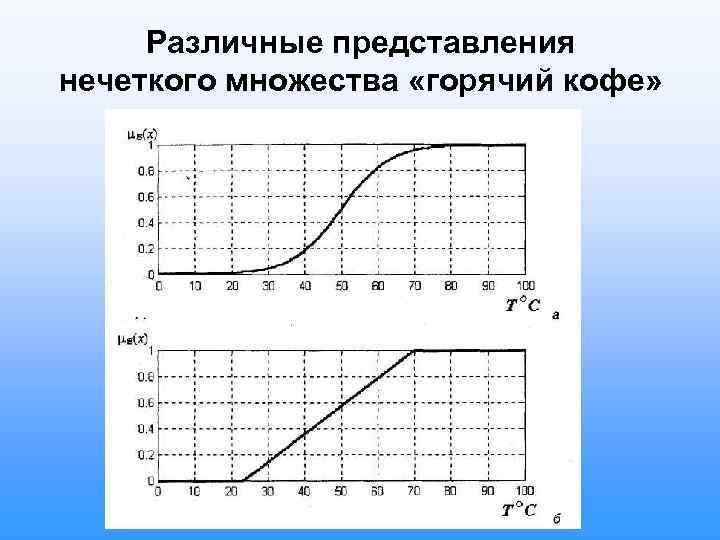
Различные представления нечеткого множества «горячий кофе»

Изоморфные понятия • Рассмотренный пример допускает обобщение на другие ситуации, связанные с представлением аналогичной нечеткой информации. В частности, целый ряд свойств технических устройств, бытовых приборов и социальных явлений могут инициировать похожие нечеткие множества. • Например, такие фразы, как "высокооплачиваемая работа", «дорогая квартира", "щедрые чаевые", «успевающий студент", «толстый учебник" порождают нечеткие множества, аналогичные рассмотренному. • Общий вид функций принадлежности таких множеств будет подобен изображенным на предыдущем рисунке.

Характерные аспекты неопределенности • Каждое из нечетких множеств допускает в общем случае неоднозначное представление, что отражает субъективную точку зрения на моделирование соответствующих практических ситуаций. • Адекватность различных представлений какого-либо понятия проверяется в последующем степенью успеха их практического использования для решения той или иной задачи. • Различие между теорией нечетких множеств и теорией вероятностей: рассмотренные варианты неопределенности имеют принципиально не стохастический характер. • Выбор аналитической функции или вида кривой для той или иной функции принадлежности с целью задания соответствующего нечеткого множества зачастую определяется соображениями удобства и простоты.

Нечеткое множество "небольшое натуральное число" : A= {<1, 1. 0>, <2, 1. 0>, <3, 0. 9>, <4, 0. 8>, <5, 0. 6>, <6, 0. 5>, <7, 0. 4>, <8, 0. 2>, <9, 0. 1>}.
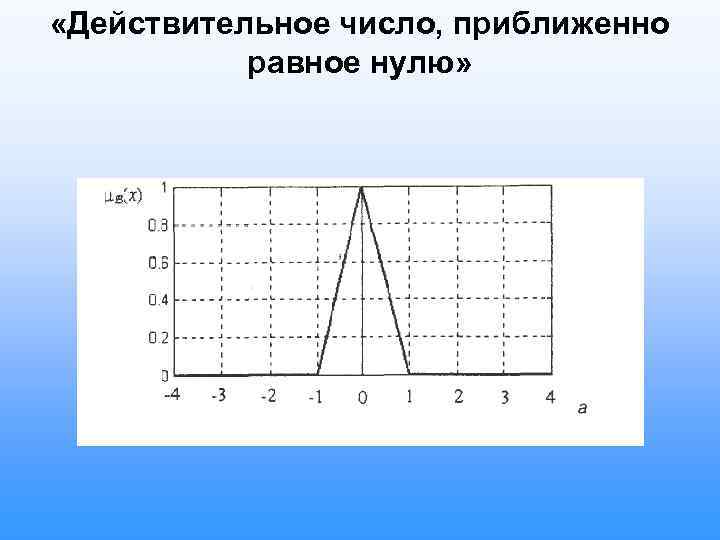
«Действительное число, приближенно равное нулю»
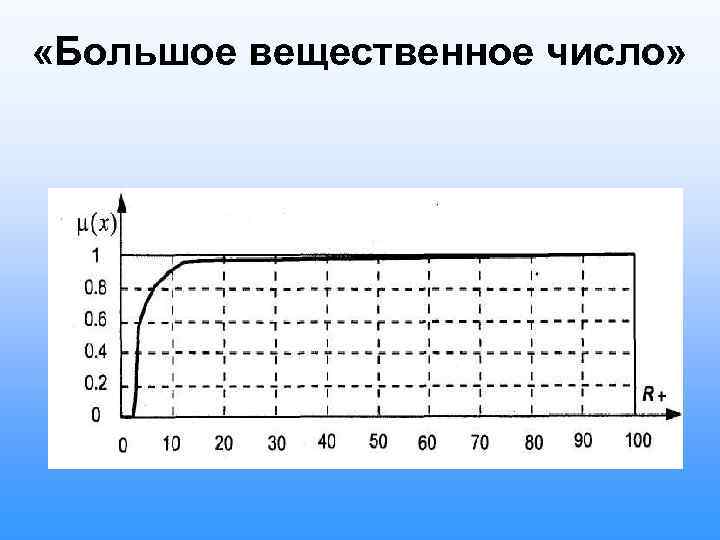
«Большое вещественное число»
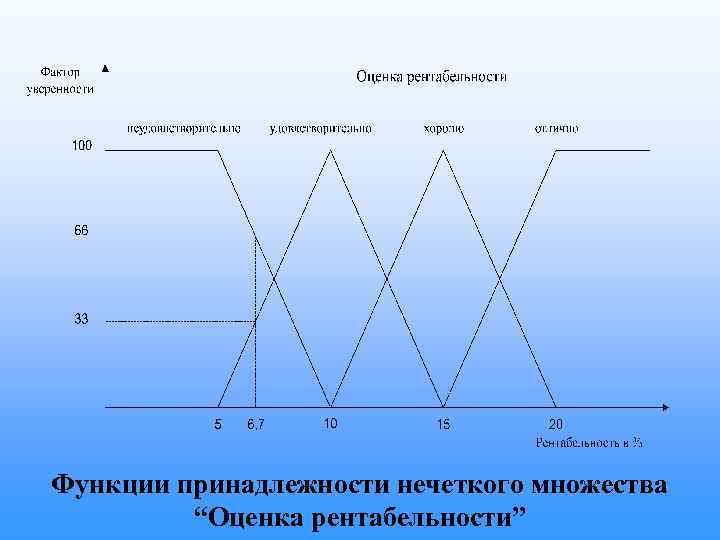
Функции принадлежности нечеткого множества “Оценка рентабельности”

Объединение факторов уверенности конъюнктивно или дизъюнктивно связанных аргументов: Конъюнкция: min (cf. A, cf. B), cf. A*cf. B/100 Дизъюнкция: max (cf. A, cf. B), cf. A+cf. B-cf. A*cf. B/100 Выбор метода объединения факторов уверенности: В посылках правил - "min/max", Левых и правых частей правил и одинаковых результатов нескольких правил – "произведение” и “сумма". Для объединения одинаковых результатов нескольких правил используется оператор “+=“, который означает не присваивание значения, а добавление значения (оператор “- =” удаляет значение).

06112014 • НЕЧЕТКАЯ АРИФМЕТИКА


Типы нечетких чисел



• Фальсификация(точного) числа представление точного числа нечетким множеством

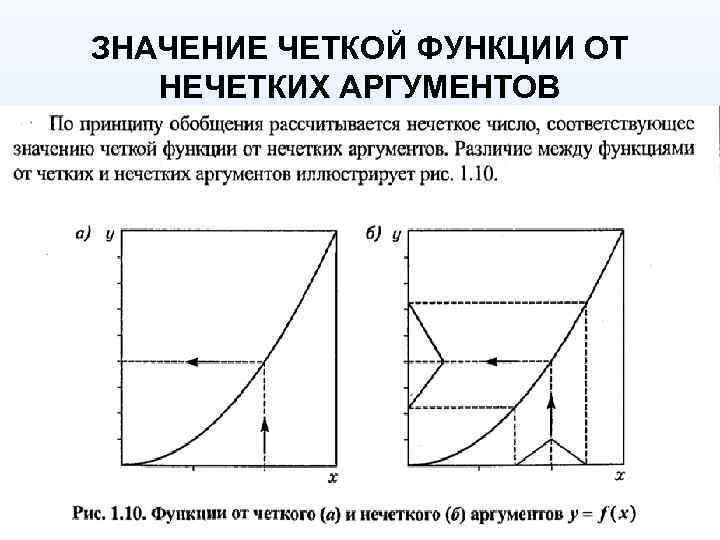
ЗНАЧЕНИЕ ЧЕТКОЙ ФУНКЦИИ ОТ НЕЧЕТКИХ АРГУМЕНТОВ

Алгоритм вычисления функции от нечетких аргументов

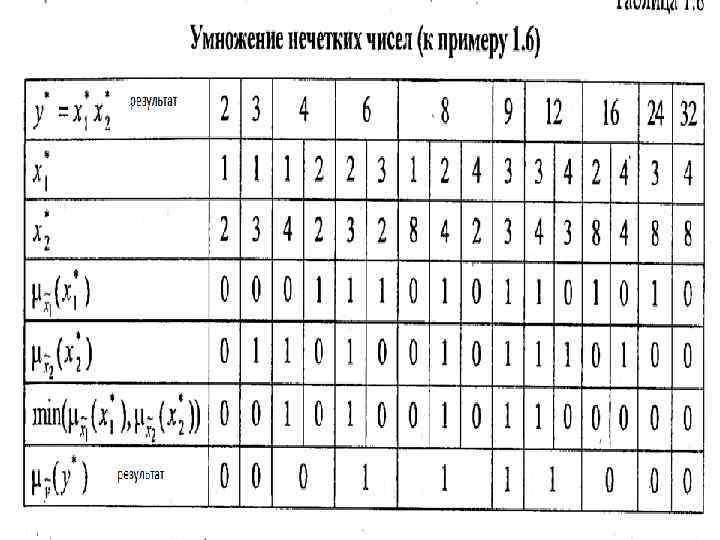

Н. И. Потанин Представ. знаний в ИС.

Н. И. Потанин Представ. знаний в ИС.

Н. И. Потанин Представ. знаний в ИС.




Нечеткие отношения операции

Четкие отношения • Отношение подмножество декартового произведения множеств. • Из определения следует, что любое отношение является множеством. Следовательно, к любому отношению применимы операции над множествами



Теоремы из линейной алгебры 1. Любая линейная функция представима матрицей. 2. Суперпозиция функций ( сложная функция) представима в виде «обратного» произведения соответствующих матриц


Вычисление матрицы нечеткого отношения

Примеры

Задания 1. Нечеткий прогноз погоды 2. Нечеткий прогноз оценки ИСи. Т

НЕЧЕТКИЕ ЗНАНИЯ

Нечеткая истинность

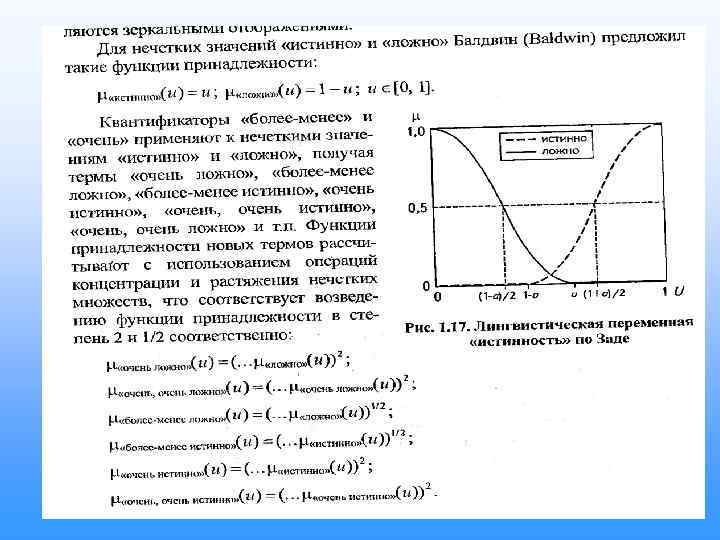
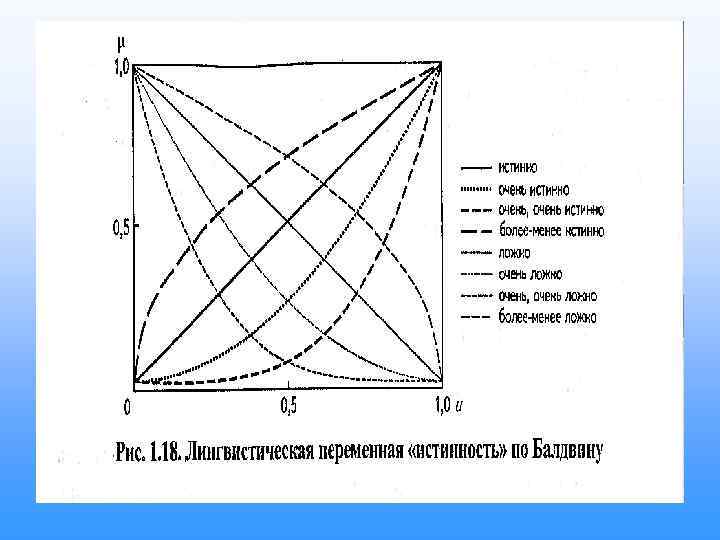

Нечеткие логические операции


Нечеткая логика


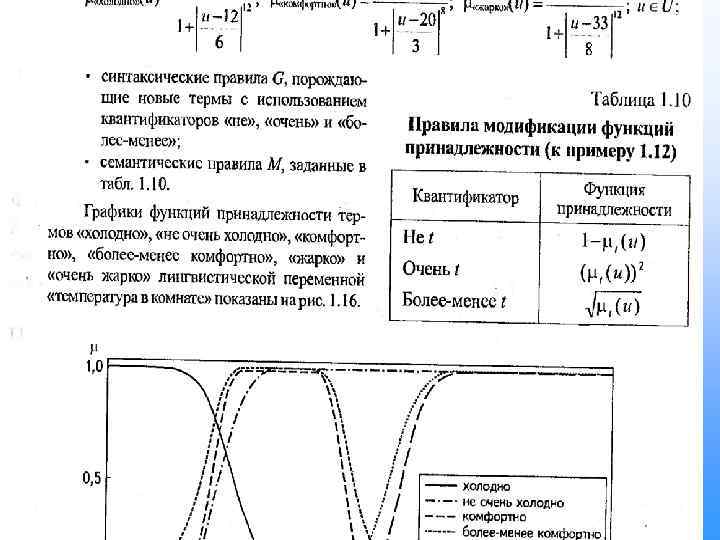

содержание • ВЫВОДЫ • СПИСОК ЛИТЕРАТУРЫ

список литературы 1.
++НЕЧЕТКИЕ МНОЖЕСТВА 19112014.pptx