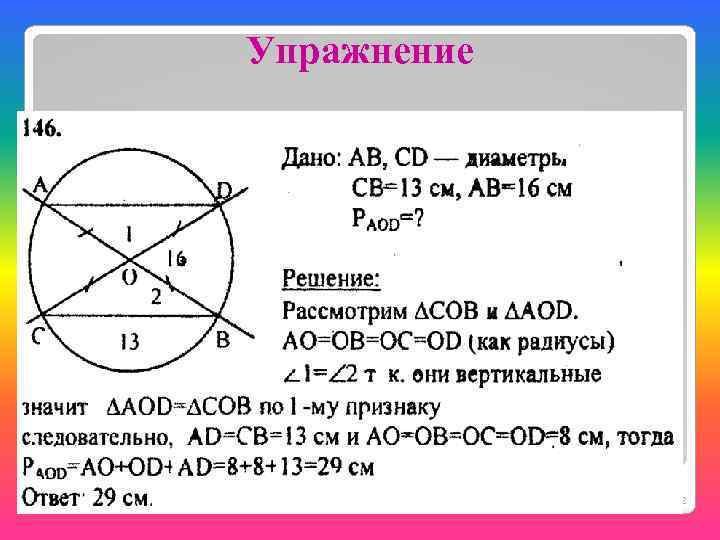
Упражнение 2 Кластер отрезок соединяющий центр с

Упражнение 2

Кластер отрезок, соединяющий центр с какой-либо точкой окружности хорда, проходящая через центр окружности геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. отрезок, соединяющий две точки окружности. Окружность Радиус окружности Диаметр Хорда

1. Построение середины отрезка. 2. Построение угла, равного данному углу. 3. Построение биссектрисы угла. 4. Построение перпендикуляра к прямой, проходящего через точку, лежащую на этой прямой. 5. Построение перпендикуляра к прямой, проходящего через точку, не лежащую на этой прямой.

В геометрии выделяют задачи на построение, которые можно решить только с помощью двух инструментов: с помощью которого можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку; 1) циркуля 2) линейки без масштабных делений, которая позволяет провести произвольную прямую, а также построить прямую, проходящую через две данные точки. IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Простейшие задачи на построение 4. Построение перпендикуляра к прямой, 5. Построение перпендикуляра к прямой, В А проходящего через точку, лежащую проходящего через точку, не лежащую О О на этой прямой. О 1. b Построение b середины отрезка. М 2. Построение угла, равного данному. М а 3. Построение биссектрисы угла. а

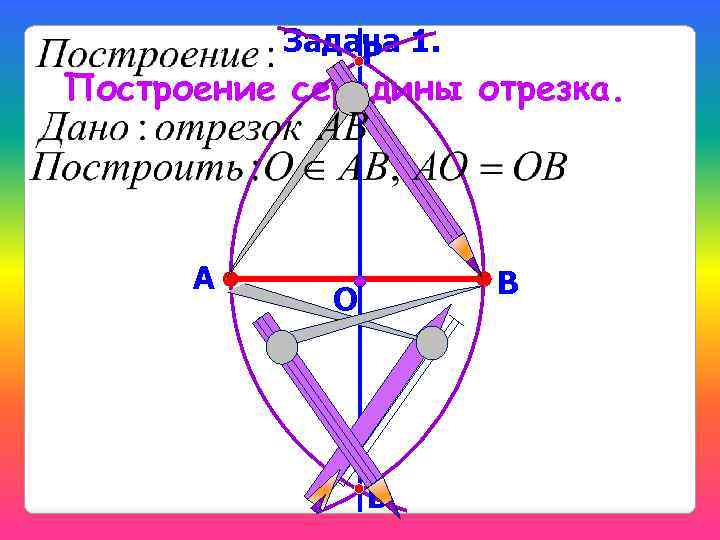Задача 1. P Построение середины отрезка. А В О D

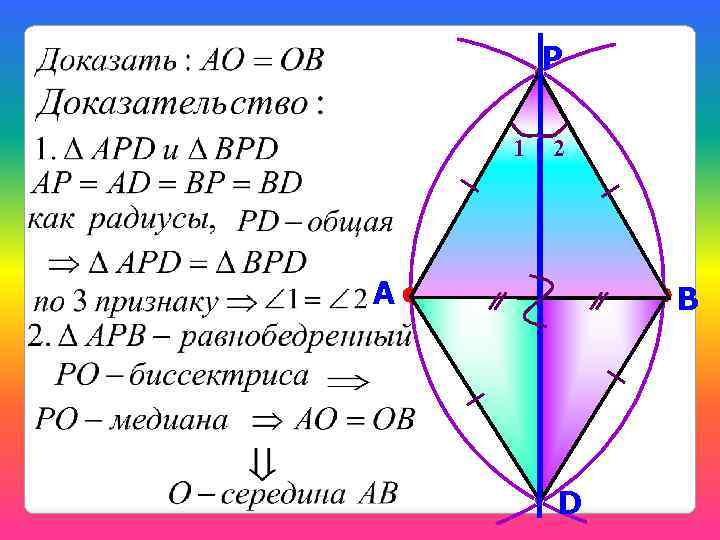P 1 А 2 В О D

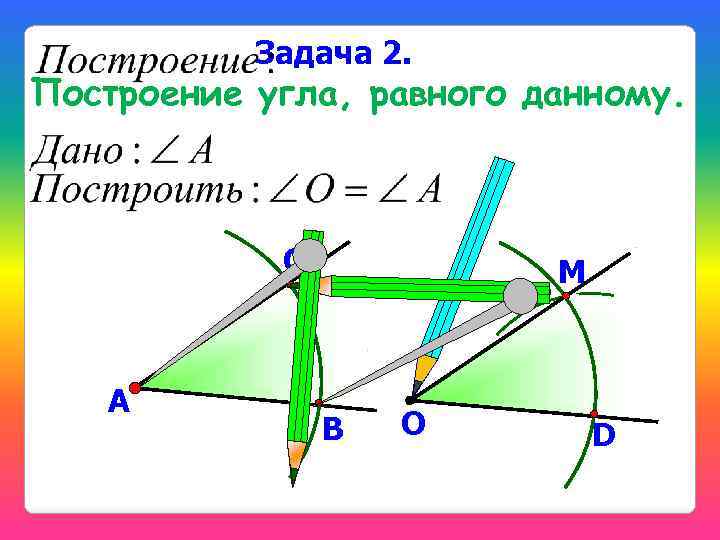Задача 2. Построение угла, равного данному. С А М В О D

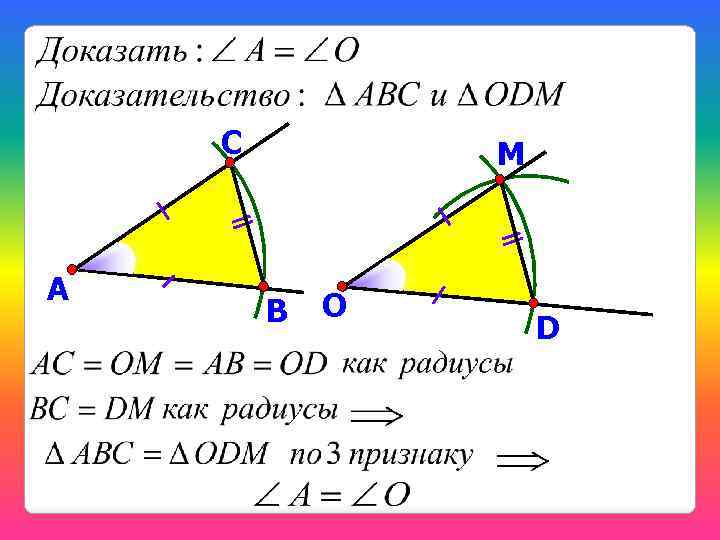С А М В О D

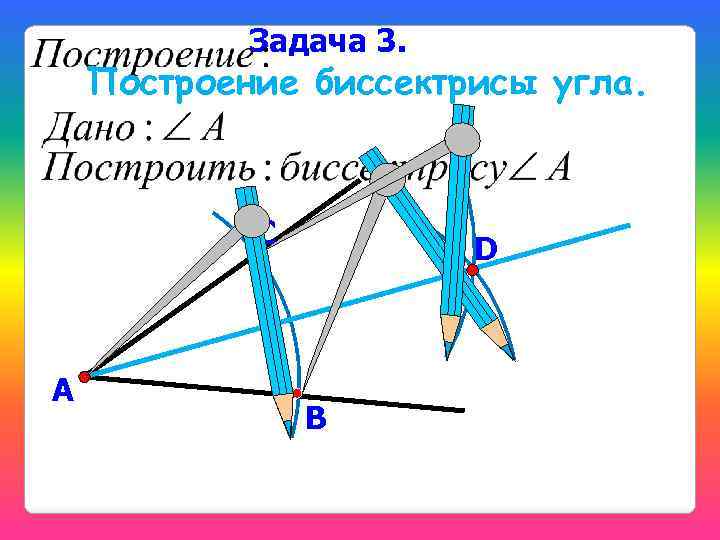Задача 3. Построение биссектрисы угла. С А D В

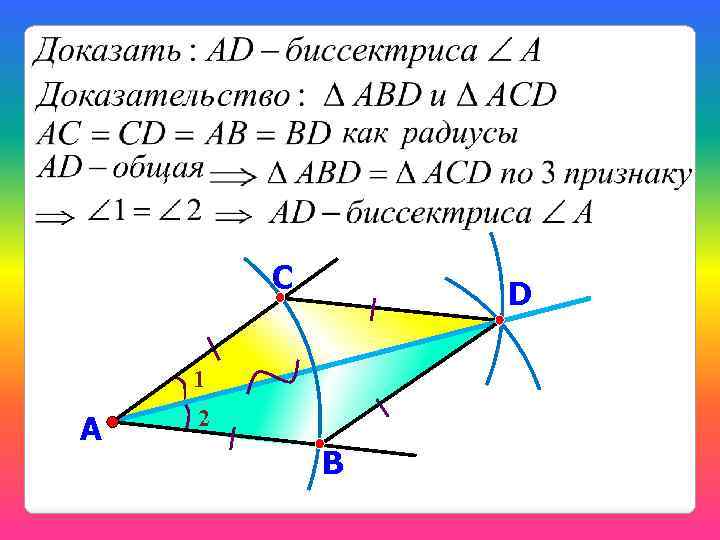С D 1 А 2 B

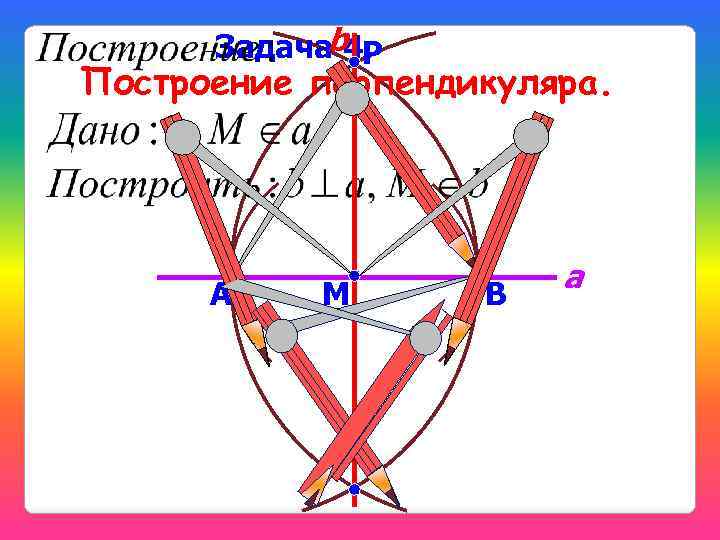b Р Задача 4. Построение перпендикуляра. А M В a

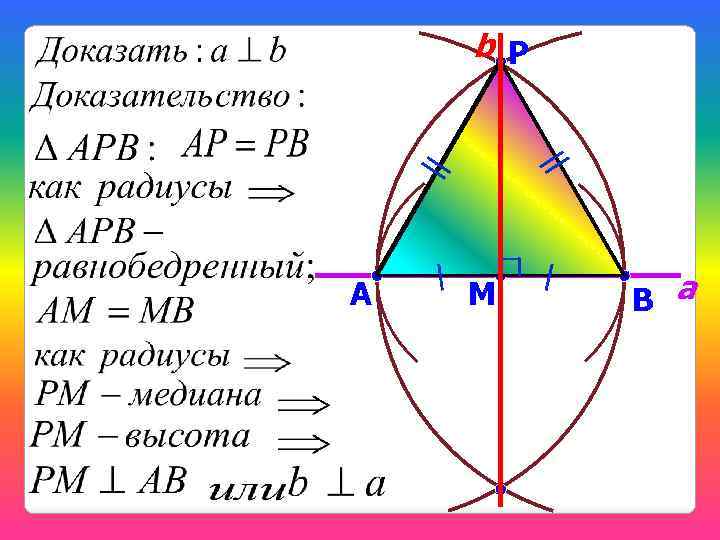b Р А M В a

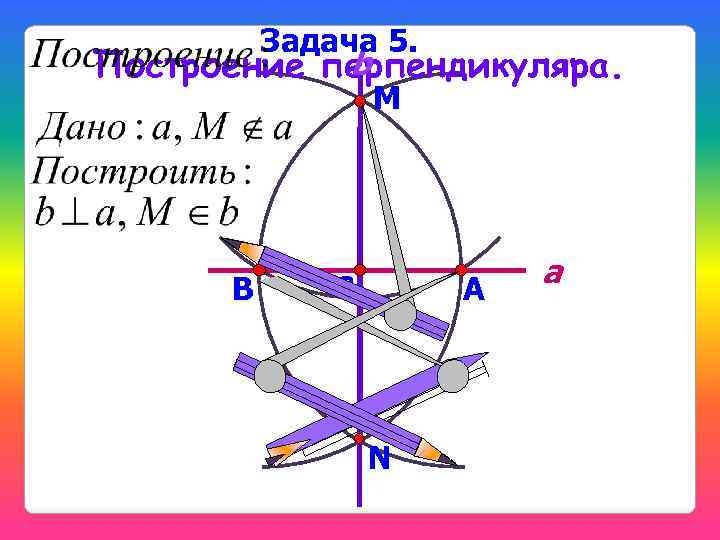Задача 5. b Построение перпендикуляра. М B C A N a

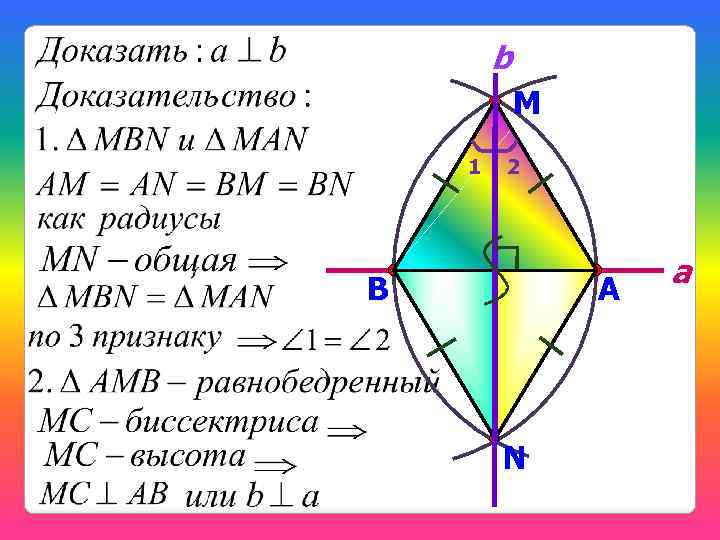b М 1 B 2 C A N a