c97df7d85acbd1ce71b74577ea409a06.ppt
- Количество слайдов: 23

Управление образования Балаковского муниципального образования. Муниципальное учреждение дополнительного образования детей Станция юных техников. Номинация: «Современные проблемы в естественных науках» . Построение сечений многогранников. Автор: Ханбикова Динара Тявфиковна; телефон 8453320597 Гражданство: Российская Федерация, Саратовская обл. , г. Балаково, Проспект Героев 29/3 -67, сош № 28, 10 Б(физикоматематический профиль) Руководитель: Серединская Наталья Ивановна (учитель математики) г. Балаково, 2009

Содержание. Введение………………………… 3 Общие сведения ……………………. . . 4 Методы построения сечений……………. . . 6 Метод вспомогательных сечений…………… 7 Метод следов………………………. 8 Задачи на построение сечения параллелепипеда. . . 9 Метод деления n-угольной призмы(пирамиды) на треугольные призмы(пирамиды)…………………. . 10 Задачи на построение сечения тетраэдра……………. . 16 Задача практического характера…………. . 18 Применение сечений в жизни……………. . . 21 Список литературы…………………. . 23 2

Введение. Данная тема занимает важное место в курсе геометрии. Метод сечений многогранников находит широкое применение в реальной жизни, его знание необходимо людям следующих профессий: архитекторам, ювелирам, дизайнерам, инженерам, токарям. Метод сечений, широко известный своей универсальностью, применяется в некоторых разделах физики, в теоретической механике, сопротивление материалов, гидравлике, в некоторых разделах высшей математики и других естественных науках и технических дисциплинах высшего образования. При работе над проектом я поставила перед собой следующие цели: 1. Исследовать какие фигуры возможны при построении сечений многогранников. 2. Выяснить какие существуют способы построения сечений(даже те которые не изучаются в школьном курсе геометрии) 3. Показать значимость данной темы и применение ее в реальной жизни. 3

Общие сведения. Для решения многих геометрических задач, связанных с тетраэдром и параллелепипедом, полезно уметь строить на рисунке их сечения различными плоскостями. Уточним, что понимается под сечение тетраэдра или параллелепипеда. Назовем секущей плоскостью тетраэдра (параллелепипеда) любую плоскость, по обе стороны от которой имеются точки данного тетраэдра (параллелепипеда). Секущая плоскость пересекает грани тетраэдра (параллелепипеда) по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра (параллелепипеда) 4

Параллелепипед: 6 – граней 12 – ребер 8 – вершин 4 – диагонали Сечения: треугольник, четырехугольник, пятиугольник, шестиугольник. Тетраэдр: 4 –грани 6 – ребер 4 – вершины Сечения : треугольник, четырехугольник. 5

Методы построения сечений. Существует три основных метода построения сечений многогранников: 1) Метод следов. 2) Метод вспомогательных сечений. 3) Комбинированный метод. Первые два метода являются разновидностями Аксиоматического метода построения сечений. Можно также выделить следующие методы построения сечений многогранников: построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости; построение сечения, проходящего через заданную прямую параллельно другой заданной прямой; построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым; построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости; построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой 6

Метод вспомогательных сечений построения сечений многогранников является в достаточной мере универсальным. В тех случаях, когда нужный след (или следы) секущей плоскости оказывается за пределами чертежа, этот метод имеет даже определенные преимущества. Вместе с тем следует иметь ввиду, что построения, выполняемые при использовании этого метода, зачастую получаются “скученными”. Тем не менее в некоторых случаях метод вспомогательных сечений оказывается наиболее рациональным. 7

Метод следов заключается в построении следов секущей плоскости на плоскость каждой грани многогранника. Построение сечения многогранника методом следов обычно начинают с построения так называемого основного следа секущей плоскости, т. е. следа секущей плоскости на плоскости основания многогранника. 8

Метод деления n-угольной призмы(пирамиды) на треугольные призмы(пирамиды) Суть этого метода состоит в следующем: из данной n-угольной призмы (пирамиды) выделяется та треугольная призма (пирамида) π, на боковых ребрах которой лежат точки, определяющие искомое сечение. Строится сечение этой треугольной призмы (пирамиды), затем строятся сечения тех треугольных призм (пирамид), которые имеют общие части с фигурой π. Рассмотрим сущность этого метода на конкретных примерах. Задача. Построит сечение пирамиды плоскостью, заданной тремя точками M, N и K на боковых гранях. Решение. Пусть SABCDE – данная пятиугольная пирамида, точка M лежит на ребре SE точка N – на ребре SA и точка К – на ребре SB. 9
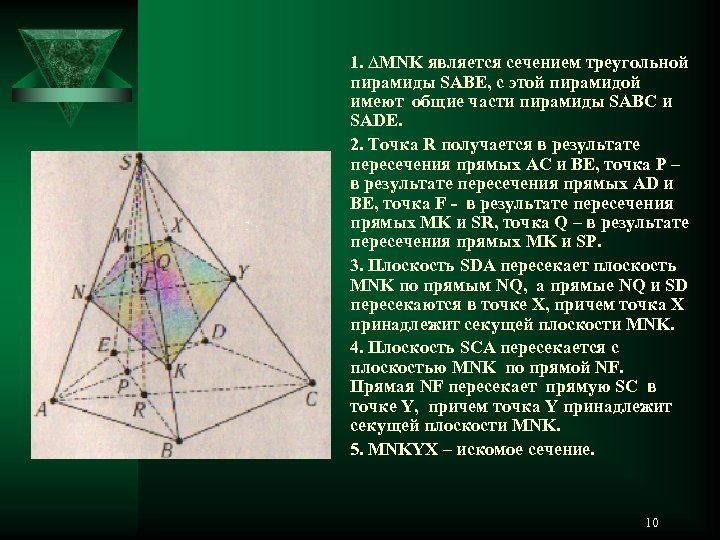
1. ∆MNK является сечением треугольной пирамиды SABE, с этой пирамидой имеют общие части пирамиды SABC и SADE. 2. Точка R получается в результате пересечения прямых AC и BE, точка P – в результате пересечения прямых AD и BE, точка F - в результате пересечения прямых MK и SR, точка Q – в результате пересечения прямых MK и SP. 3. Плоскость SDA пересекает плоскость MNK по прямым NQ, а прямые NQ и SD пересекаются в точке X, причем точка X принадлежит секущей плоскости MNK. 4. Плоскость SCA пересекается с плоскостью MNK по прямой NF. Прямая NF пересекает прямую SC в точке Y, причем точка Y принадлежит секущей плоскости MNK. 5. MNKYX – искомое сечение. 10

Задачи на построение сечения параллелепипеда. Построить сечение призмы ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через точки P, Q, R (точки указаны на чертеже. Решение. Построим след секущей плоскости на плоскость нижнего основания призмы. Рассмотрим грань АА 1 В 1 В. В этой грани лежат точки сечения P и Q. Проведем прямую PQ. Продолжим прямую PQ, которая принадлежит сечению, до пересечения с прямой АВ. Получим точку S 1, принадлежащую следу. Аналогично получаем точку S 2 пересечением прямых QR и BC. Прямая S 1 S 2 - след секущей плоскости на плоскость нижнего основания призмы. Прямая S 1 S 2 пересекает сторону AD в точке U, сторону CD в точке Т. Соединим точки P и U, так как они лежат в одной плоскости грани АА 1 D 1 D. Аналогично получаем TU и RT. PQRTU – искомое сечение. 11

Построить сечение параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через точки M, N, P (точки указаны на чертеже Решение. Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проходящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда. Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения. Так как точка M также принадлежит плоскости сечения и пересекает прямую АА 1 в некоторой точке Х. Точки X и N лежат в одной плоскости грани АА 1 D 1 D, соединим их и получим прямую XN. Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A 1 B 1 C 1 D 1, параллельную прямой NP. Эта прямая пересечет сторону В 1 С 1 в точке Y. Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX. 12

Построить сечение параллелепипеда AEFQRKRG через точки R, P, Q. Решение: 1. RP, т. к R и P принадлежат (RKPG) 2. QR, т. к. Q и R принадлежат (ARGQ) 3. PQ , т. к. P и Q принадлежат (PGQF). 4. RPQ – искомое сечение 13

Построить сечение куба плоскостью, проходящей через точки: M принад. AA 1 D 1 D, N принад. A 1 B 1 C 1 D 1, K принад. DD 1 C 1 C 1. ММ 1 ║ АА 1; 2. NN 1 ║ AA 1, NN 1 = AA 1; 3. M N; 4. M 1 N 1; 5. MN ∩ M 1 N 1; 6. KK 1║CC 1; 7. N K; 8. N 1 K 1; 9. NK ∩ N 1 K 1 = Y; 10. X Y; 11. XY ∩ AD = P; 12. XY ∩ DC = Q; 13. P M; 14. PM ∩ AA 1 = R; 15. Q K; 16. QK ∩ CC 1 = F; 17. PR ∩ A 1 D 1 = Z; 18. Z N; 19. ZN ∩ A 1 B 1 = O; 20. ZN ∩ C 1 D 1 = S; 21. S F; 22. R O 23. ROSFQP – искомое сечение. B 1 z A 1 O C 1 N D 1 M B A M 1 K N 1 P Q D KC Y 1 14

Постройте сечение параллелепипеда АВСDA 1 B 1 C 1 D 1, через точки А, С, F лежащая на ребре А 1 D 1, через точку Е лежащую на ребре D 1 C 1. Построение: 1. EF, т. к. E и F принадлежат (A 1 B 1 C 1 D 1) 2. ЕС, т. к. Е и С принадлежат (DD 1 C 1 С) 3. АС, т. к. А и С принадлежат (АВСD) 4. АF, т. к. А и F принадлежат (АА 1 D 1 D). 5. АFЕС – искомое сечение 15

Задачи на построение сечения тетраэдра. Построить сечение тетраэдра АВСD, проходящее через точки Р, N, M принадлежащие ребрам AD, DB, DC. Построение 1. PN , т. к. P и N принадлеж. (ADВ) 2. MN, т. к. M и N принадлеж. (ВDC) 3. PM, т. к. P и M принадлеж. (АDC) 4. РNM – искомое сечение 16
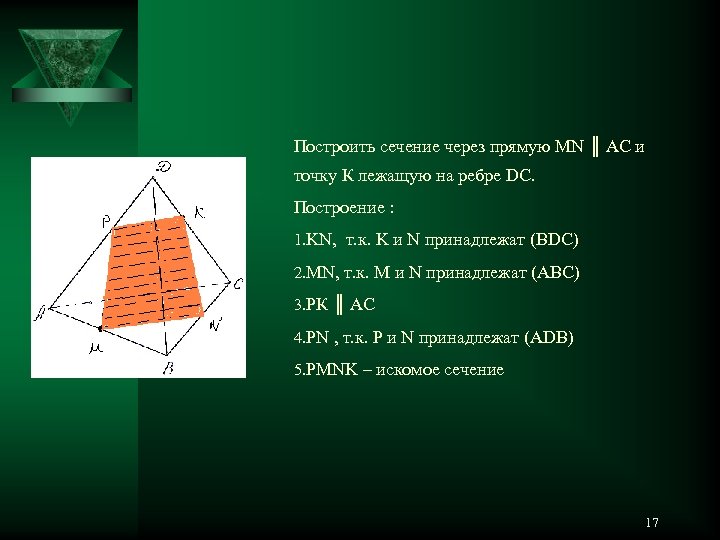
Построить сечение через прямую MN ║ АС и точку К лежащую на ребре DC. Построение : 1. KN, т. к. K и N принадлежат (ВDC) 2. MN, т. к. M и N принадлежат (АВC) 3. РК ║ АС 4. PN , т. к. P и N принадлежат (ADВ) 5. PMNK – искомое сечение 17

Задача практического характера. Здание ювелирного салона построено в виде равностороннего тетраэдра. Здание имеет два этажа. Высота стен салона составляет 9 м. Пол второго этажа необходимо покрыть мраморной плиткой, имеющей размеры 50*40 см. Какое примерное количество плиток необходимо приобрести, если стены каждого этажа составляют 3 м. Дано: BACD-равносторонний тетраэдр, BQ=3 м, BC=9 м. Найти: n - количество плиток; 18

Решение: Р. м. ∆ADC и ∆MNQ углы QMN=CAD(соот. сонапр. ) углы MQN=ACD(соот. сонапр. ) => ∆ADC ~ ∆MNQ (по 2 м углам) => = k ( т. к. высота стен каждого этажа=3 м) => k= Р. м ∆ADC – равносторонний DK – высота, биссектриса, медиана => AK=KC= , где а=9 м Р. м ∆ADK – прямоугольный, по теореме Пифагора => = = - ; ; 19

Для того чтобы покрыть пол второго этажа мраморной плиткой необходимо приобрести приблизительно 43 плитки. 20

Применение сечения в жизни. 1. 2. 3. 4. 5. Строительство В чертежном проецировании (проецирование в трех плоскостях) В ремонтных работах В бытовых работах В пищевой промышленности. 21

6. В архитектуре ( мозаика, пирамиды). 7. В огранке ювелирных изделий. 22

Список литературы. 1. 2. 3. 4. далее. . . Геометрические построения в курсе средней школы, А. О. Корнеева, Саратов, Издательство «Лицей» , 2003. «Энциклопедия Кирилла и Мефодия» , 2003 г. Казаков П. Г. , Параллельные проекции и методы и решение конструктивных задач. Учпедгиз, 1960. Четверухин Н. Ф. Методы геометрических построений, Учпедгиз, 1952. 23
c97df7d85acbd1ce71b74577ea409a06.ppt