1bf095b8daafbb582e568ec6f0533ed1.ppt
- Количество слайдов: 24

Updating Finite Element Models to Match Ground Vibration Test Data Chan-gi Pak, Ph. D. Leader, Structural Dynamics Group Aerostructures Branch (Code RS) NASA Dryden Flight Research Center Structural Dynamics Group Chan-gi Pak-1

Structural Dynamics Group q Functionality v Aeroelastic & Aeroservoelastic System Analysis, Clearance, Monitoring, & Research q Skills v Structural Dynamic Finite Element Modeling, Analyses, & Tool Development Ø Use Pro. E, MSC/PATRAN, & MSC/NASTRAN codes for Structural Modeling & Analyses Ø In-house Tool Development for Structural Dynamic, Aeroelastic, & Aeroservoelastic Analyses v Ground Vibration Test and Finite Element Model Update Ø Improve Structural Dynamic FEM if needed v Aeroelastic and Aeroservoelastic Analyses Ø Flutter, Buzz, Divergence, and Closed-Loop Flutter Analyses Ø Subsonic and Supersonic Flight Regimes: Use Linear Lifting Surface Codes (ZAERO or MSC/NASTRAN) Ø Transonic Flight Regime: Use 3 D CFD Codes (CFL 3 D version 4 or CAPTSDv etc. ) v Structural Optimization with Stress/Strain and Flutter Constraints Ø Based on MSC/NASTRAN code Structural Dynamics Group Chan-gi Pak-2
Structural Dynamics Group (continued) q Skills (continued) v Structural Mode Interaction Test and Flight Control Model Update Ø Improve Flight Control Model if needed v Maneuver Load Alleviation and Control Ø Based on Minimization of the Maximum Bending Moment and/or Shear Force v Active Aeroelastic Control and Vibration Suppression Ø Based on Modern and Adaptive Control Techniques v Flight Flutter Testing & On-Line System Identification (Flutterometer) Ø Flutter Boundary Identification based on Flight Test Data Ø Linear and Nonlinear Robust Aeroservoelastic System ID Structure Ø Time-frequency-scale (wavelet, HHT) Identification v Structural Health Monitoring Ø Use GVT & Mode Matching Technique Aeroservoelasticity Ø Linear/Nonlinear ID Methods Control Structural Dynamics Group Aerodynamic Chan-gi Pak-3

Introduction q Everyone believes the test data except for the experimentalist, and no one believes the finite element model except for the analyst. v Some of the discrepancies come from analytical Finite Element modeling uncertainties, noise in the test results, and/or inadequate sensor and actuator locations. q MIL-STD-1540 C Section 6. 2. 10 v Test Requirements for Launch, Upper-Stage, & Space Vehicles v Less than 3% and 10% frequency errors for the primary and secondary modes, respectively v Less than 10% off-diagonal terms in mass matrix q AFFTC-TIH-90 -001 (Structures Flight Test Handbook) v If measured mode shapes are going to be associated with a finite element model of the structure, it will probably need to be adjusted to match the lumped mass modeling of the analysis. v Based on the measured mode shape matrix [F] and the analytical mass matrix [M] , the following operation is performed. The results is near diagonalization of the resulting matrix with values close to 1 on the diagonal and values close to zero in the off-diagonal terms. Experimental reality dictates that the data will not produce exact unity or null values, so 10 percent of these targets are accepted as good orthogonality and the data can be confidently correlated with the finite element model. Structural Dynamics Group Chan-gi Pak-4

Orthogonality Requirements for Structural Dynamics M: Mass matrix K: Stiffness matrix F: Mode shaped (Eigen matrix) w: Frequencies (Eigen Values) q Guarantee linear independency between mode shapes q Superposition principle can be used for the aeroelastic and aeroservoelastic analyses Structural Dynamics Group Chan-gi Pak-5
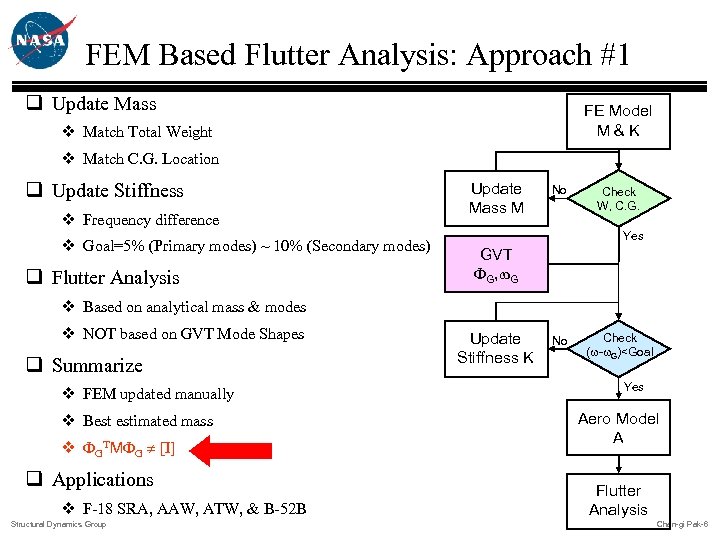
FEM Based Flutter Analysis: Approach #1 q Update Mass FE Model M&K v Match Total Weight v Match C. G. Location q Update Stiffness v Frequency difference v Goal=5% (Primary modes) ~ 10% (Secondary modes) q Flutter Analysis Update Mass M No Check W, C. G. Yes GVT FG, w. G v Based on analytical mass & modes v NOT based on GVT Mode Shapes q Summarize v FEM updated manually v Best estimated mass v FGTMFG [I] q Applications v F-18 SRA, AAW, ATW, & B-52 B Structural Dynamics Group Update Stiffness K No Check (w-w. G)<Goal Yes Aero Model A Flutter Analysis Chan-gi Pak-6
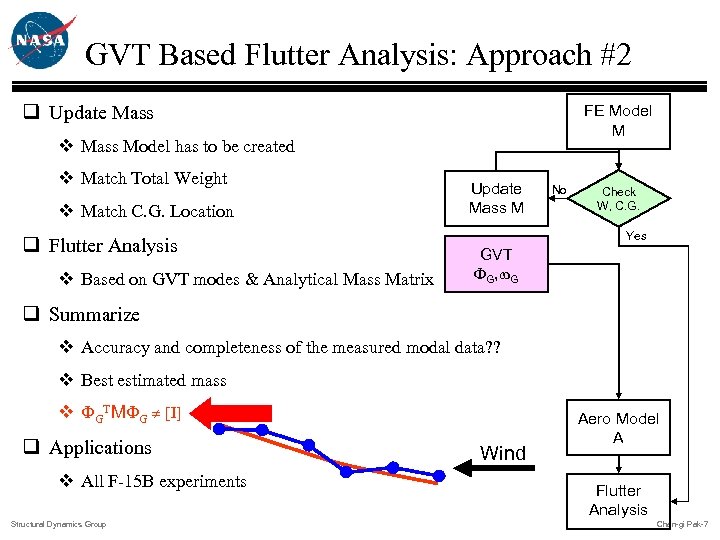
GVT Based Flutter Analysis: Approach #2 q Update Mass FE Model M v Mass Model has to be created v Match Total Weight v Match C. G. Location q Flutter Analysis v Based on GVT modes & Analytical Mass Matrix Update Mass M No Check W, C. G. Yes GVT FG, w. G q Summarize v Accuracy and completeness of the measured modal data? ? v Best estimated mass v FGTMFG [I] q Applications v All F-15 B experiments Structural Dynamics Group Wind Aero Model A Flutter Analysis Chan-gi Pak-7
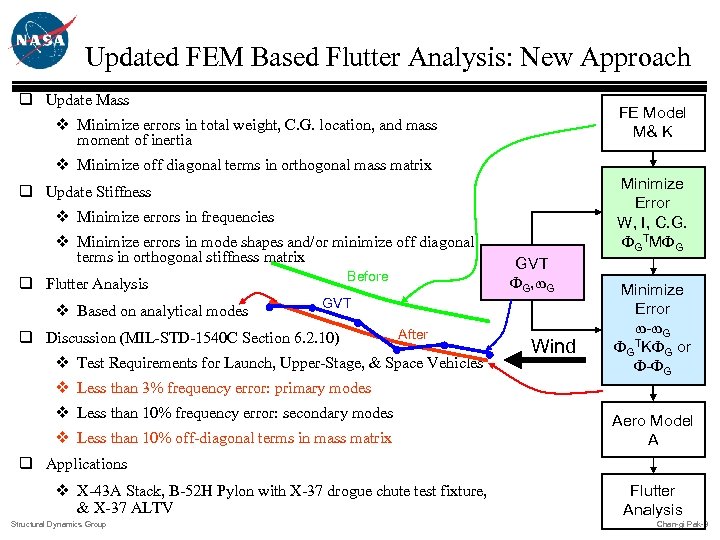
Updated FEM Based Flutter Analysis: New Approach q Update Mass FE Model M& K v Minimize errors in total weight, C. G. location, and mass moment of inertia v Minimize off diagonal terms in orthogonal mass matrix Minimize Error W, I, C. G. FGTMFG q Update Stiffness v Minimize errors in frequencies v Minimize errors in mode shapes and/or minimize off diagonal terms in orthogonal stiffness matrix Before q Flutter Analysis v Based on analytical modes GVT FG, w. G GVT q Discussion (MIL-STD-1540 C Section 6. 2. 10) After v Test Requirements for Launch, Upper-Stage, & Space Vehicles Wind Minimize Error w-w. G TKF or FG G F-FG v Less than 3% frequency error: primary modes v Less than 10% frequency error: secondary modes v Less than 10% off-diagonal terms in mass matrix Aero Model A q Applications v X-43 A Stack, B-52 H Pylon with X-37 drogue chute test fixture, & X-37 ALTV Structural Dynamics Group Flutter Analysis Chan-gi Pak-8

Model Update Technique q Step 1: Mass Properties v v To start optimization procedure inside the feasible domain Infeasible Match Total Mass Match CG Locations Match Mass Moment of Inertias Statement Number Constraints 1 J 1 = W-WG Unconstraint 2 J 2 = X-XG |J 1| < e 3 J 3 = Y-YG |Ji| < e i=1, 2 4 J 4 = Z-ZG |Ji| < e i =1, … 3 5 J 5 = IXX-(IXX)G |Ji| < e i =1, … 4 6 J 6 = IYY-(IYY)G |Ji| < e i =1, … 5 7 J 7 = IZZ-(IZZ)G |Ji| < e i =1, … 6 8 J 8 = IXY-(IXY)G |Ji| < e i =1, … 7 9 J 9 = IYZ-(IYZ)G |Ji| < e i =1, … 8 10 Structural Dynamics Group Objective Function J 10 = IZX-(IZX)G Feasible |Ji| < e i =1, … 9 Chan-gi Pak-9

Model Update Technique (Continued) q Step 2: Improve Mass Matrix v Orthonormalized Mass Matrix: M = FT M F v Minimize J Such that, ¢ |W-WG| < e : Total Mass ¢ |X-XG| < e, |Y-YG| < e, & |Z-ZG| < e: CG Locations ¢ |IXX-(IXX)G| < e, |IYY-(IYY)G| < e, |IZZ-(IZZ)G| < e, |IXY-(IXY)G| < e, |IYZ(IYZ)G| < e, |IZX-(IZX)G| < e: Mass Moment of Inertia at CG ¢ Positive Definiteness of Lumped Masses Structural Dynamics Group Chan-gi Pak-10

Model Update Technique (continued) q Step 3: Frequencies and Mode Shapes v Option 1: Minimize Errors in Frequencies and off-diagonal terms in K ¢ ¢ v Orthonormalized Stiffness Matrix: K = FT K F Minimize J Option 2: Minimize Errors in Frequencies and Mode Shapes ¢ Eigen-Solver is based on Ø Ø ¢ Subspace Iteration Method Simplified Approach Minimize J where, i=1, . . , n j=1, …, m Structural Dynamics Group n: number of modes m: number of sensors Chan-gi Pak-11
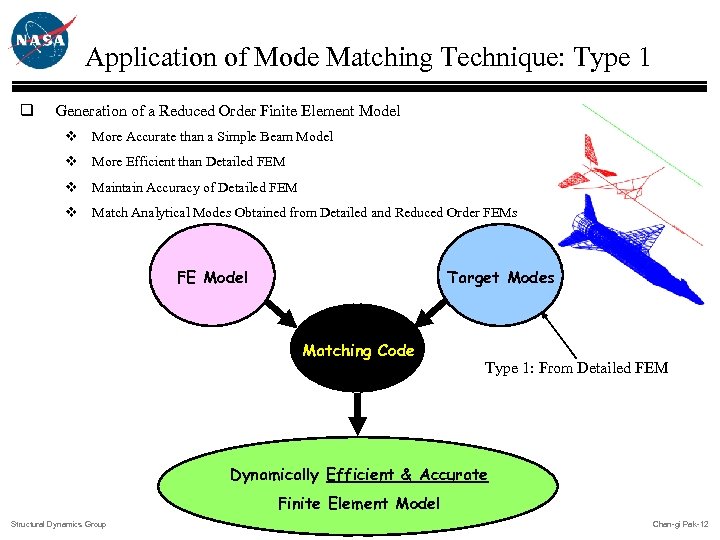
Application of Mode Matching Technique: Type 1 q Generation of a Reduced Order Finite Element Model v More Accurate than a Simple Beam Model v More Efficient than Detailed FEM v Maintain Accuracy of Detailed FEM v Match Analytical Modes Obtained from Detailed and Reduced Order FEMs Target Modes FE Model Matching Code Type 1: From Detailed FEM Dynamically Efficient & Accurate Finite Element Model Structural Dynamics Group Chan-gi Pak-12
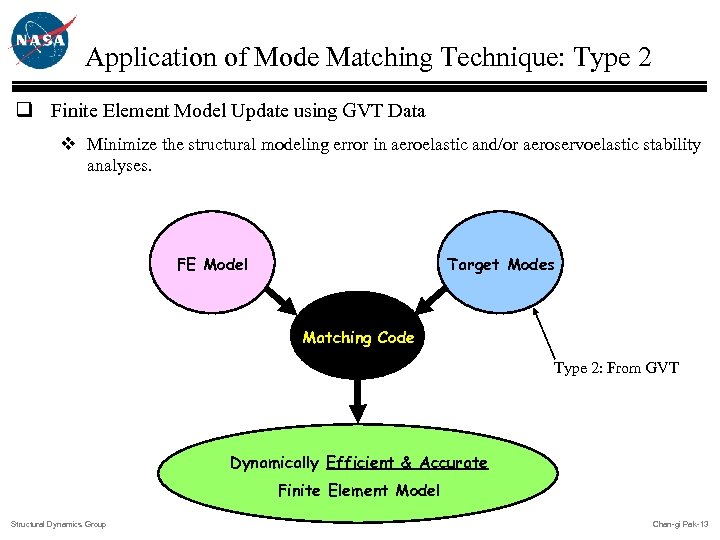
Application of Mode Matching Technique: Type 2 q Finite Element Model Update using GVT Data v Minimize the structural modeling error in aeroelastic and/or aeroservoelastic stability analyses. Target Modes FE Model Matching Code Type 2: From GVT Dynamically Efficient & Accurate Finite Element Model Structural Dynamics Group Chan-gi Pak-13
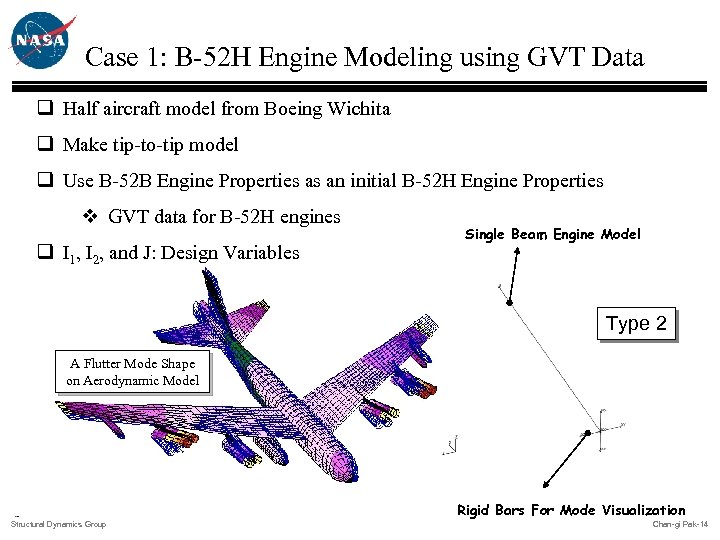
Case 1: B-52 H Engine Modeling using GVT Data q Half aircraft model from Boeing Wichita q Make tip-to-tip model q Use B-52 B Engine Properties as an initial B-52 H Engine Properties v GVT data for B-52 H engines q I 1, I 2, and J: Design Variables Single Beam Engine Model Type 2 A Flutter Mode Shape on Aerodynamic Model Rigid Bars For Mode Visualization Structural Dynamics Group Chan-gi Pak-14
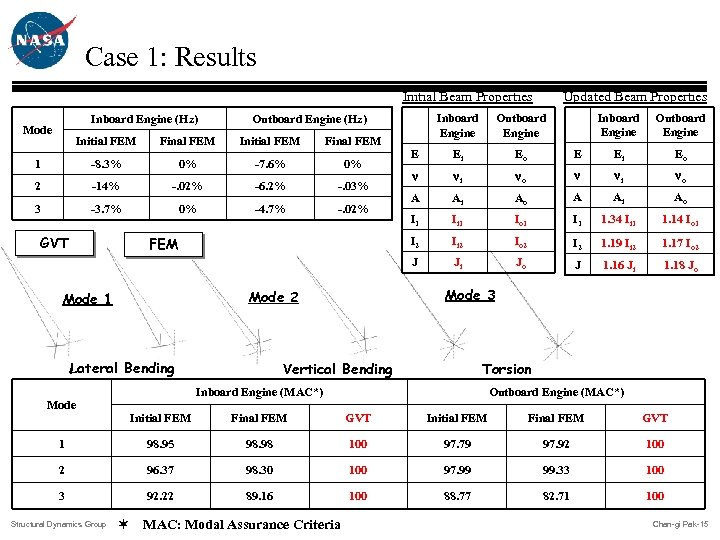
Case 1: Results Updated Beam Properties Initial FEM Final FEM 1 -8. 3% 0% -7. 6% 0% 2 -14% -. 02% -6. 2% -. 03% 3 -3. 7% 0% -4. 7% -. 02% FEM Ei Eo no n ni no Ai Ao A Ai Ao I 1 Ii 1 Io 1 I 1 1. 34 Ii 1 1. 14 Io 1 Ii 2 Io 2 I 2 1. 19 Ii 2 1. 17 Io 2 Ji Jo J 1. 16 Ji 1. 18 Jo Outboard Engine E Ei Eo n ni A Mode 3 Mode 2 Lateral Bending Mode E J Final FEM Mode 1 Outboard Engine Inboard Engine Outboard Engine (Hz) Initial FEM GVT Inboard Engine I 2 Inboard Engine (Hz) Mode Vertical Bending Torsion Inboard Engine (MAC*) Outboard Engine (MAC*) Initial FEM Final FEM GVT 1 98. 95 98. 98 100 97. 79 97. 92 100 2 96. 37 98. 30 100 97. 99 99. 33 100 3 92. 22 89. 16 100 88. 77 82. 71 100 Structural Dynamics Group ¬ MAC: Modal Assurance Criteria Chan-gi Pak-15
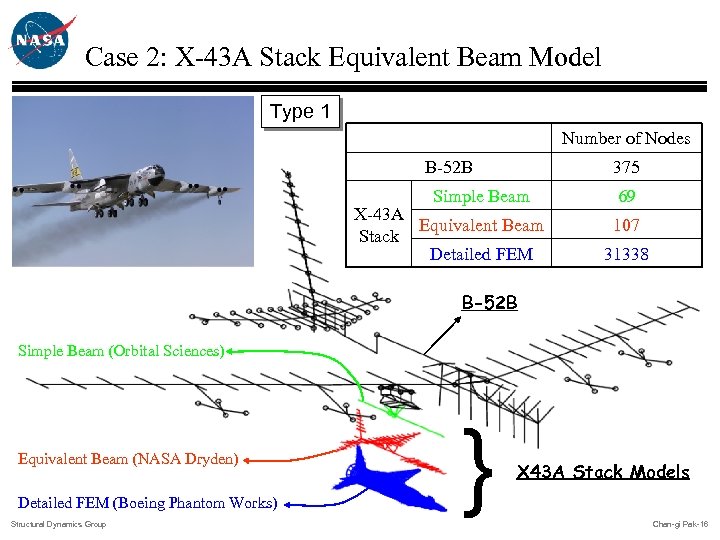
Case 2: X-43 A Stack Equivalent Beam Model Type 1 Number of Nodes B-52 B 375 Simple Beam X-43 A Equivalent Beam Stack Detailed FEM 69 107 31338 B-52 B Simple Beam (Orbital Sciences) Equivalent Beam (NASA Dryden) Detailed FEM (Boeing Phantom Works) Structural Dynamics Group } X 43 A Stack Models Chan-gi Pak-16

Case 2: Results Frequencies (Hz) Mode Simple Beam Equivalent Beam Detailed FEM 1 31% -. 09%(99. 3) f 1 2 83% -. 02%(89. 6) f 2 3 168% 2%(94. 8) f 3 4 200% 1%(91. 1) f 4 5 159% -1. 1%(82. 1) f 5 Detail Equivalent Mode 1 Mode 5 Second Lateral Bending (*): MAC Value Mode 2 Mode 3 Yawing Structural Dynamics Group Pitching Mode 4 Lateral Bending Vertical Bending Chan-gi Pak-17
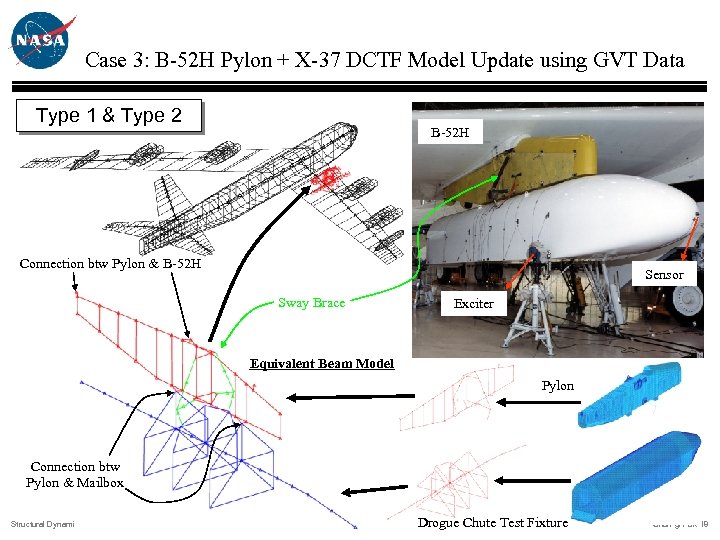
Case 3: B-52 H Pylon + X-37 DCTF Model Update using GVT Data Type 1 & Type 2 B-52 H Connection btw Pylon & B-52 H Sensor Sway Brace Exciter Equivalent Beam Model Pylon Connection btw Pylon & Mailbox Structural Dynamics Group Drogue Chute Test Fixture Chan-gi Pak-18
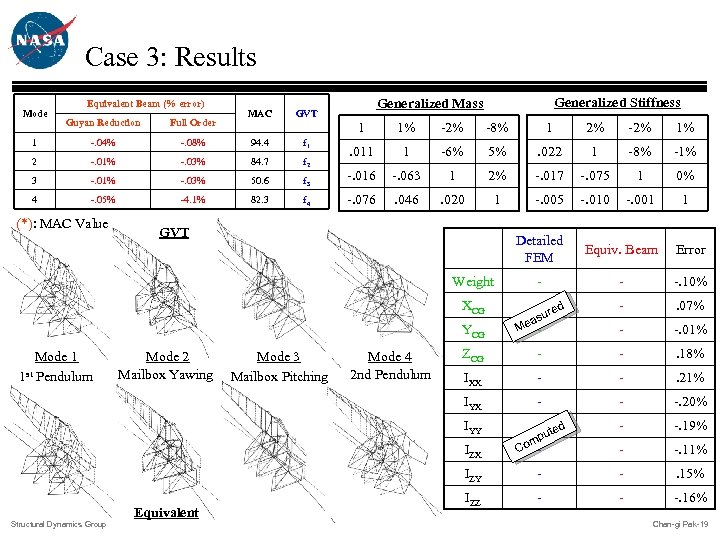
Case 3: Results Mode Equivalent Beam (% error) MAC Guyan Reduction Full Order 1 -. 04% -. 08% 94. 4 f 1 2 -. 01% -. 03% 84. 7 f 2 3 -. 01% -. 03% 50. 6 4 -. 05% -4. 1% 82. 3 (*): MAC Value Generalized Stiffness Generalized Mass GVT 1 1% -2% -8% 1 2% -2% 1% . 011 1 -6% 5% . 022 1 -8% -1% f 3 -. 016 -. 063 1 2% -. 017 -. 075 1 0% f 4 -. 076 . 046 . 020 1 -. 005 -. 010 -. 001 1 GVT - red su ea M - - . 07% - -. 01% ZCG - - . 18% IXX - - . 21% - - -. 20% - ted pu om. C - -. 19% IZX - -. 11% IZY Equivalent -. 10% IYY Structural Dynamics Group - IYX Mode 4 2 nd Pendulum - YCG Mode 3 Mailbox Pitching Error XCG Mode 2 Mailbox Yawing Equiv. Beam Weight Mode 1 1 st Pendulum Detailed FEM - - . 15% IZZ - - -. 16% Chan-gi Pak-19
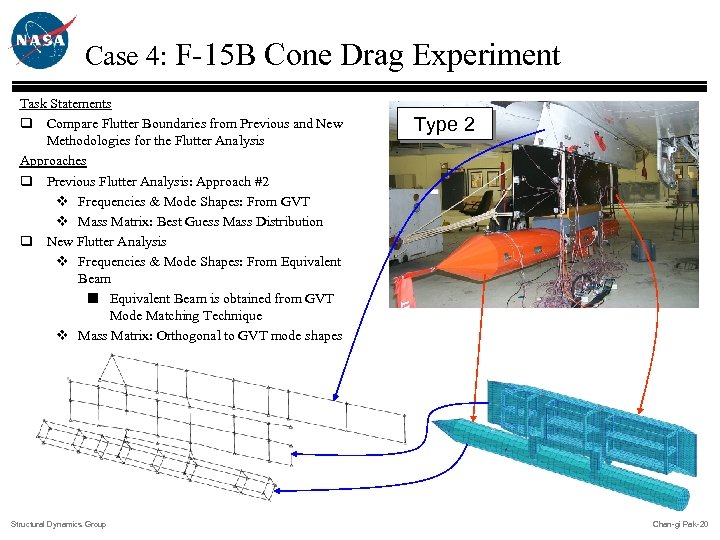
Case 4: F-15 B Cone Drag Experiment Task Statements q Compare Flutter Boundaries from Previous and New Methodologies for the Flutter Analysis Approaches q Previous Flutter Analysis: Approach #2 v Frequencies & Mode Shapes: From GVT v Mass Matrix: Best Guess Mass Distribution q New Flutter Analysis v Frequencies & Mode Shapes: From Equivalent Beam ¢ Equivalent Beam is obtained from GVT Mode Matching Technique v Mass Matrix: Orthogonal to GVT mode shapes Structural Dynamics Group Type 2 Chan-gi Pak-20
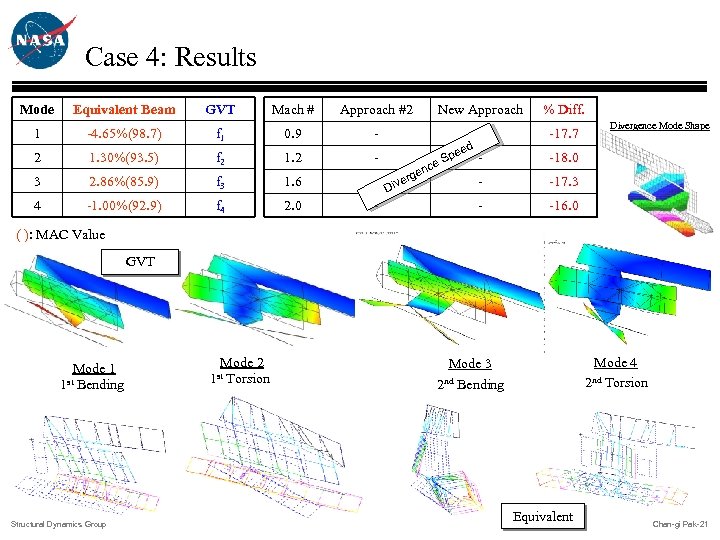
Case 4: Results Mode Equivalent Beam GVT Mach # Approach #2 New Approach % Diff. 1 -4. 65%(98. 7) f 1 0. 9 - - -17. 7 2 1. 30%(93. 5) f 2 1. 2 - 3 2. 86%(85. 9) f 3 1. 6 4 -1. 00%(92. 9) f 4 2. 0 - Diverg - d ee - c en p e. S Divergence Mode Shape -18. 0 - -17. 3 - -16. 0 ( ): MAC Value GVT Mode 1 st Bending 1 Structural Dynamics Group Mode 2 Torsion 1 st Mode 4 2 nd Torsion Mode 3 2 nd Bending Equivalent Chan-gi Pak-21

Structural Dynamic Research Activities at NASA Dryden Flight Research Center Structural Dynamics Group Chan-gi Pak-22

Project Supports & Researches (FY 05 - Present) q High Altitude Long Endurance Remotely Operated Aircraft v Create and Update Beam Equivalent Model for a High Aspect Ratio Wing v Develop New GVT Methodology v Preparing Structural Dynamics R&D Proposals for Modeling/Simulation/Control q F-15 B Quiet Spike Boom v Update F-15 B & Quite Spike Boom Models for the Open-Loop Flutter Clearance q F-15 B LIFT v For Space Shuttle Return to Flight v Flutter Clearance q ATW 2 v Flutter Clearance and Sensor Research q AAW v ASE Flight Research q F-15 IFCS v ASE Clearance with Adaptive Controller Structural Dynamics Group HALE ROA ATW 2 F-15 B Quiet Spike AAW F-15 B LIFT F-15 IFCS Chan-gi Pak-23

Project Supports & Researches (FY 02 - FY 04) q Helios Mishap Investigation v Structural Dynamic & Flutter Analyses q X-43 A Ship 1 v Independent Mishap Investigation v Closed-Loop Flutter Analysis q X-43 A Ship 2 & Ship 3 v B-52 B Captive Carry Flutter Clearance q X-37 ALTV, Pylon, and DCF v B-52 H Captive Carry Flutter Clearance q ALTAIR (UAV) v Structural Dynamic & Flutter Analyses q F-15 B CDE v Flutter Clearance q ATW 1 v Flutterometer Research q X-45 A (UCAV) v GVT Structural Dynamics Group Helios ALTAIR X-43 A Ship 1 F-15 B CDE X-43 A Ship 2 & 3 ATW 1 X-37 ALTV, Pylon, & DCF X-45 A Chan-gi Pak-24
1bf095b8daafbb582e568ec6f0533ed1.ppt