Universally Composable Symbolic Analysis of Cryptographic Protocols Ran

Universally Composable Symbolic Analysis of Cryptographic Protocols Ran Canetti and Jonathan Herzog 6 March 2006 The author's affiliation with The MITRE Corporation is provided for identification purposes only, and is not intended to convey or imply MITRE's concurrence with, or support for, the positions, opinions or viewpoints expressed by the author.

Universally Composable Automated Analysis of Cryptographic Protocols Ran Canetti and Jonathan Herzog 6 March 2006 The author's affiliation with The MITRE Corporation is provided for identification purposes only, and is not intended to convey or imply MITRE's concurrence with, or support for, the positions, opinions or viewpoints expressed by the author.

Overview n This talk: symbolic analysis can guarantee universally composable (UC) key exchange • n n n (Paper also includes mutual authentication) Symbolic (Dolev-Yao) model: high-level framework • • Messages treated symbolically; adversary extremely limited Despite (general) undecidability, proofs can be automated Result: symbolic proofs are computationally sound (UC) • • For some protocols For strengthened symbolic definition of secrecy With UC theorems, suffices to analyze single session • Implies decidability!

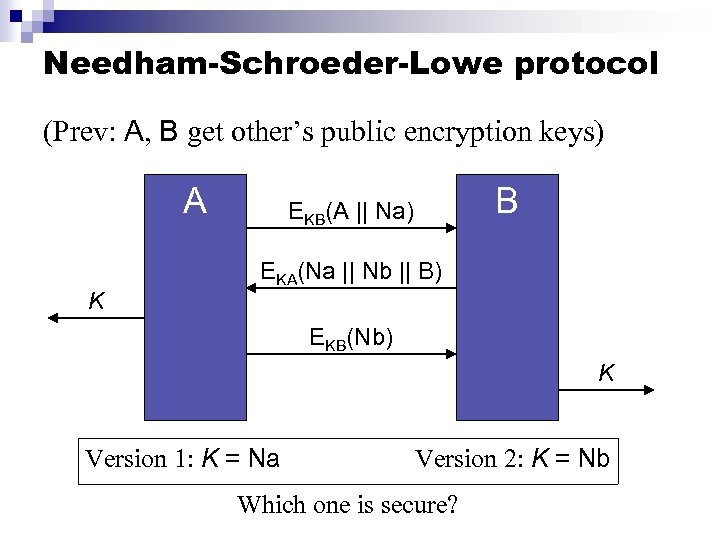
Needham-Schroeder-Lowe protocol (Prev: A, B get other’s public encryption keys) A K B EKB(A || Na) EKA(Na || Nb || B) EKB(Nb) K Version 1: K = Na Version 2: K = Nb Which one is secure?

Two approaches to analysis n Standard (computational) approach: reduce attacks to weakness of encryption n Alternate approach: apply methods of the symbolic model • • • Originally proposed by Dolev & Yao (1983) Cryptography without: probability, security parameter, etc. Messages are parse trees Countable symbols for keys (K, K’, …), names (A, B, …) and nonces (N, N’, Na, Nb, …) n Encryption ( EK(M) ) pairing ( M || N ) are constructors n • Participants send/receive messages n Output some key-symbol

The symbolic adversary n Explicitly enumerated powers • • • Interact with countable number of participants Knowledge of all public values, non-secret keys Limited set of re-write rules: M 1 , M 2 M 1 || M 2 M, K EK(M), K-1 M 1 || M 2 M 1 , M 2 EK(M) M

‘Traditional’ symbolic secrecy n Conventional goal for symbolic secrecy proofs: “If A or B output K, then no sequence of interactions/rewrites can result in K” n Undecidable in general [EG, HT, DLMS] but: • • Decidable with bounds [DLMS, RT] Also, general case can be automatically verified in practice n n Demo 1: analysis of both NSLv 1, NSLv 2 So what? • Symbolic model has weak adversary, strong assumptions • We want computational properties! • …But can we harness these automated tools?

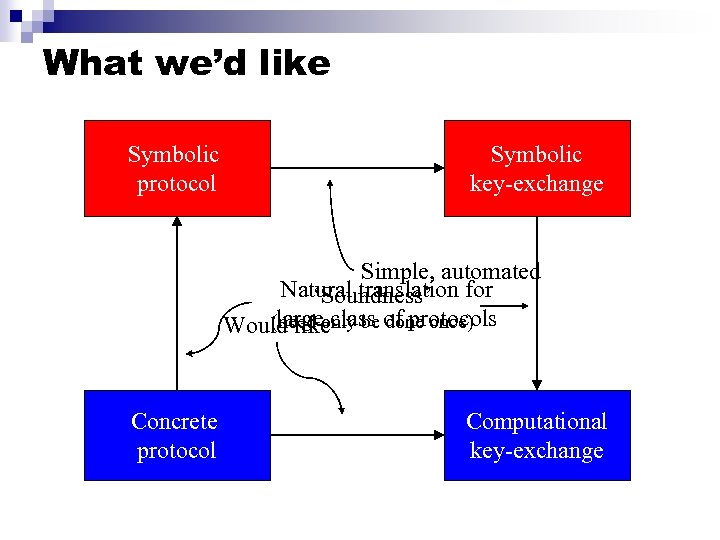
What we’d like Symbolic protocol Symbolic key-exchange Simple, automated Natural translation for ‘Soundness’ large (need only be done once) Would likeclass of protocols Concrete protocol Computational key-exchange

Some previous work General area: n n n [AR]: soundness for indistinguishability • Passive adversary [MW, BPW]: soundness for general trace properties • Includes mutual authentication; active adversary Many, many others Key-exchange in particular (independent work): n n [BPW]: (later) [CW]: soundness for key-exchange • Traditional symbolic secrecy implies (weak) computational secrecy

Limitations of ‘traditional’ secrecy n Big question: Can ‘traditional’ symbolic secrecy imply standard computational definitions of secrecy? n n Unfortunately, no Counter-example: • Demo: NSLv 2 satisfies traditional secrecy • Cannot provide real-or-random secrecy in standard models • Falls prey to the ‘Rackoff’ attack

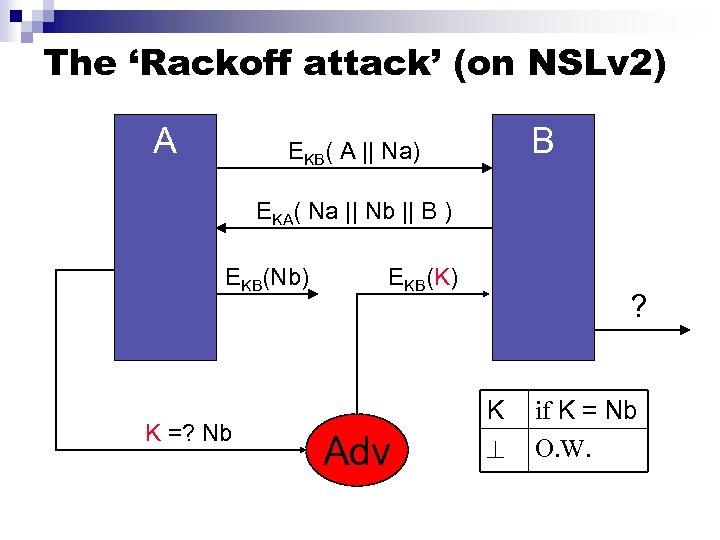
The ‘Rackoff attack’ (on NSLv 2) A B EKB( A || Na) EKA( Na || Nb || B ) EKB(Nb) K =? Nb EKB(K) Adv ? K if K = Nb O. W.

Achieving soundness n Soundness requires new symbolic definition of secrecy n [BPW]: ‘traditional’ secrecy + ‘non-use’ n • • Thm: new definition implies secrecy (in their framework) But: must analyze infinite concurrent sessions and all resulting protocols Here: ‘traditional’ secrecy + symbolic real-or-random • • • Non-interference property; close to ‘strong secrecy’ [B] Thm: new definition equivalent to UC secrecy Demonstrably automatable (Demo 2) Suffices to consider single session! (Infinite concurrency results from joint-state UC theorems) Implies decidability (forthcoming)

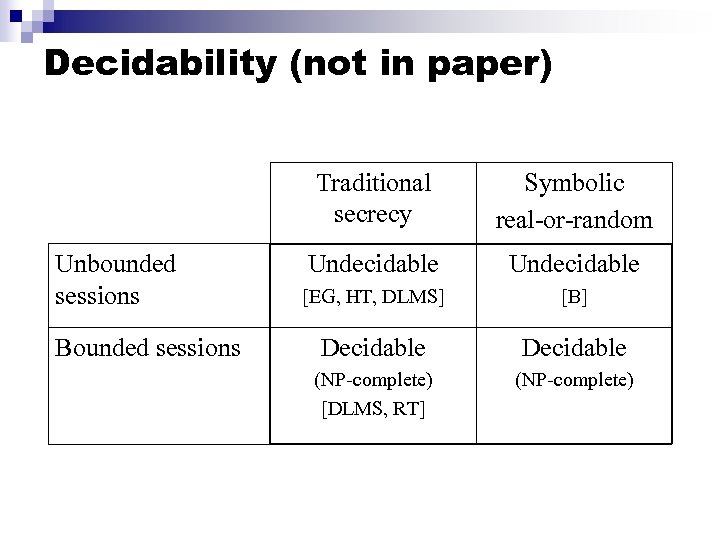
Decidability (not in paper) Traditional secrecy Unbounded sessions Bounded sessions Symbolic real-or-random Undecidable [EG, HT, DLMS] [B] Decidable (NP-complete) [DLMS, RT] (NP-complete)

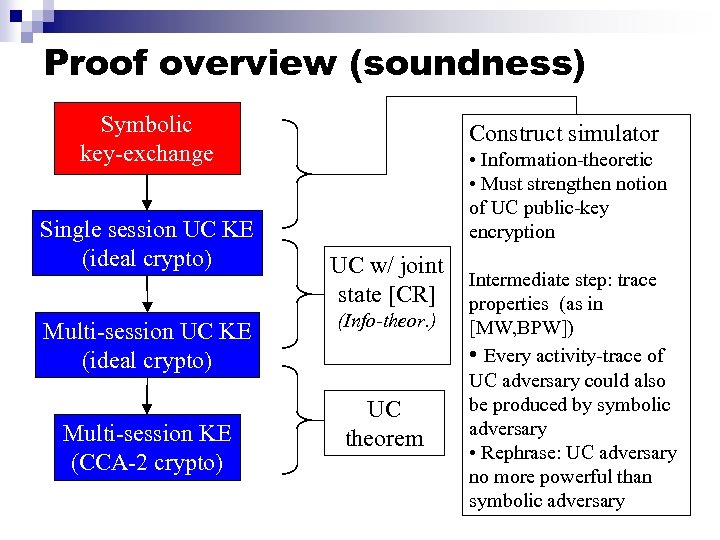
Proof overview (soundness) Symbolic key-exchange Single session UC KE (ideal crypto) Multi-session KE (CCA-2 crypto) Construct simulator • Information-theoretic • Must strengthen notion of UC public-key encryption UC w/ joint state [CR] (Info-theor. ) UC theorem Intermediate step: trace properties (as in [MW, BPW]) • Every activity-trace of UC adversary could also be produced by symbolic adversary • Rephrase: UC adversary no more powerful than symbolic adversary

Summary & future work n n Result: symbolic proofs are computationally sound (UC) • • For some protocols For strengthened symbolic definition of secrecy With UC theorems, suffices to analyze single session • Implies decidability! Additional primitives • • Have public-key encryption, signatures [P] Would like symmetric encryption, MACs, PRFs… Symbolic representation of other goals • Commitment schemes, ZK, MPC…

Backup slides

Two challenges 1. Traditional secrecy is undecidable for: • Unbounded message sizes [EG, HT] or • Unbounded number of concurrent sessions (Decidable when both are bounded) [DLMS] 2. Traditional secrecy is unsound • Cannot imply standard security definitions for • computational key exchange Example: NSLv 2 (Demo)

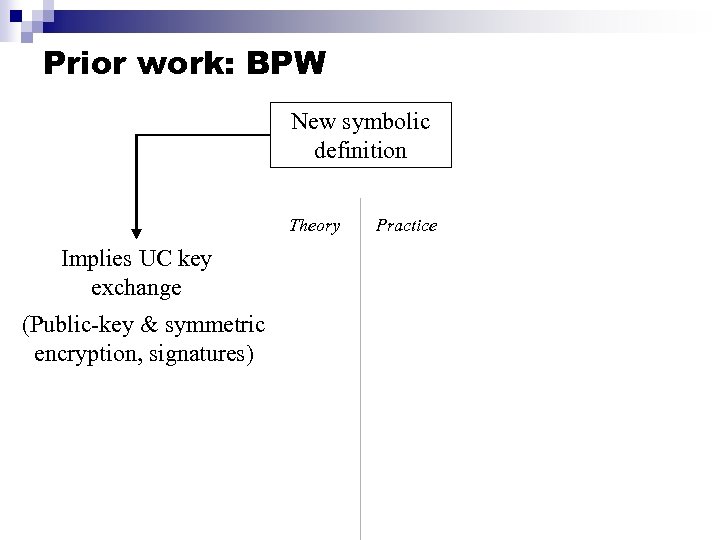
Prior work: BPW New symbolic definition Theory Implies UC key exchange (Public-key & symmetric encryption, signatures) Practice

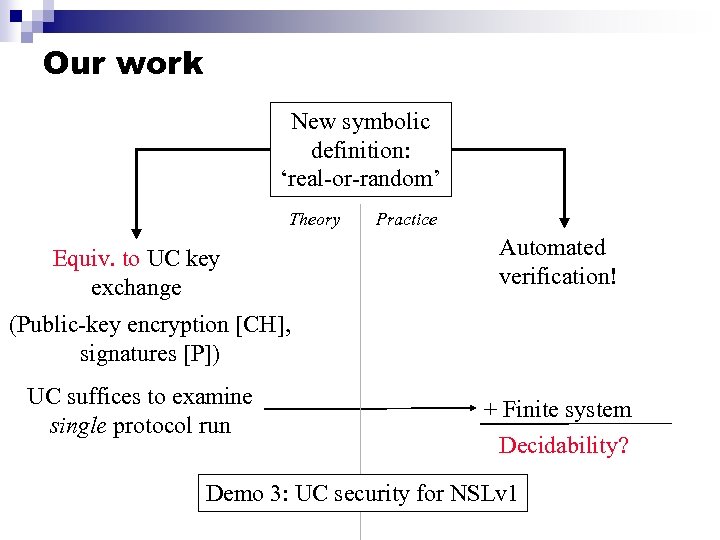
Our work New symbolic definition: ‘real-or-random’ Theory Equiv. to UC key exchange Practice Automated verification! (Public-key encryption [CH], signatures [P]) UC suffices to examine single protocol run + Finite system Decidability? Demo 3: UC security for NSLv 1

Our work: solving the challenges n n Soundness: requires new symbolic definition of secrecy • • Ours: purely symbolic expression of ‘real-or-random’ security Result: new symbolic definition equivalent to UC key exchange UC theorems: sufficient to examine single protocol in isolation • • Thus, bounded numbers of concurrent sessions Automated verification of our new definition is decidable!… Probably

Summary n Summary: • Symbolic key-exchange sound in UC model • Computational crypto can now harness symbolic tools • Now have the best of both worlds: security and automation! n Future work

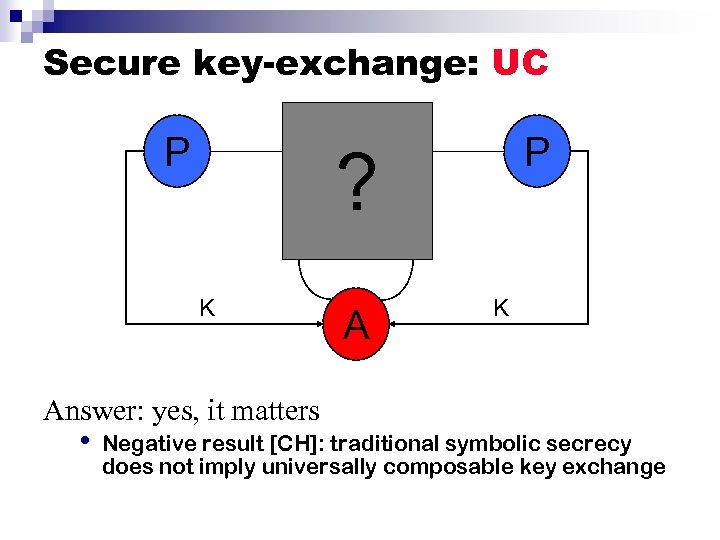
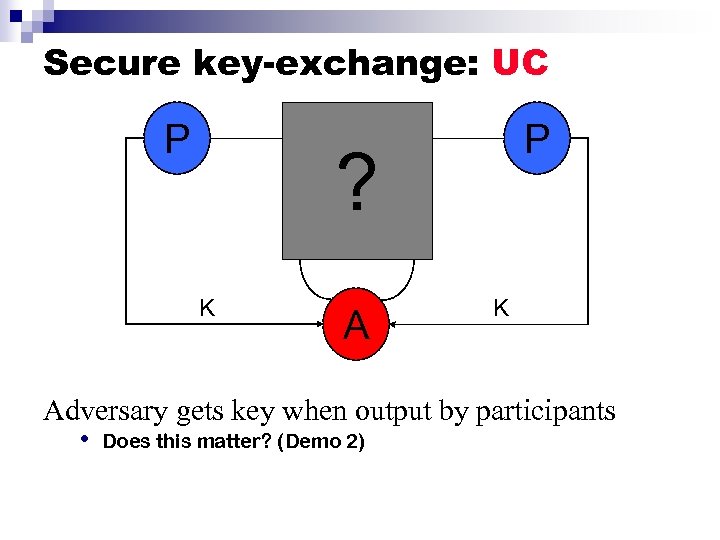
Secure key-exchange: UC P P ? K Answer: yes, it matters • Negative result [CH]: traditional symbolic secrecy does not imply universally composable key exchange

Secure key-exchange: UC P P F ? S K Adversary gets key when output by participants • Does this matter? (Demo 2)

Secure key-exchange [CW] P K, K’ P A n Adversary interacts with participants • Afterward, receives real key, random key • Protocol secure if adversary unable to distinguish n NSLv 1, NSLv 2 satisfy symbolic def of secrecy • Therefore, NSLv 1, NSLv 2 meet this definition as well

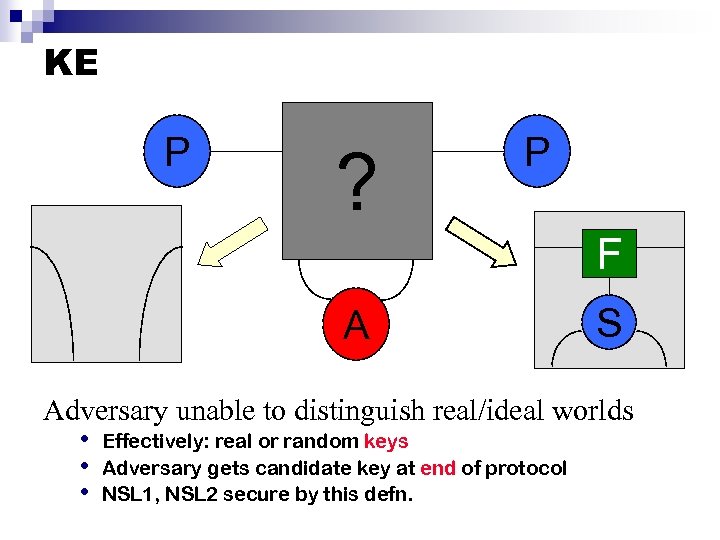
KE P ? P F A S Adversary unable to distinguish real/ideal worlds • Effectively: real or random keys • Adversary gets candidate key at end of protocol • NSL 1, NSL 2 secure by this defn.

Analysis strategy Dolev-Yao protocol Dolev-Yao key-exchange Simple, automated Main result of talk Natural translation for (Need only be done protocols large Would likeclass of once) Concrete protocol UC key-exchange functionality

“Simple” protocols n n Concrete protocols that map naturally to Dolev-Yao framework Two cryptographic operations: • • Randomness generation Encryption/decryption n n (This talk: asymmetric encryption) Example: Needham-Schroeder-Lowe {P 1, N 1}K 2 P 1 {P 2, N 1, N 2}K 1 {N 2}K 2 P 2

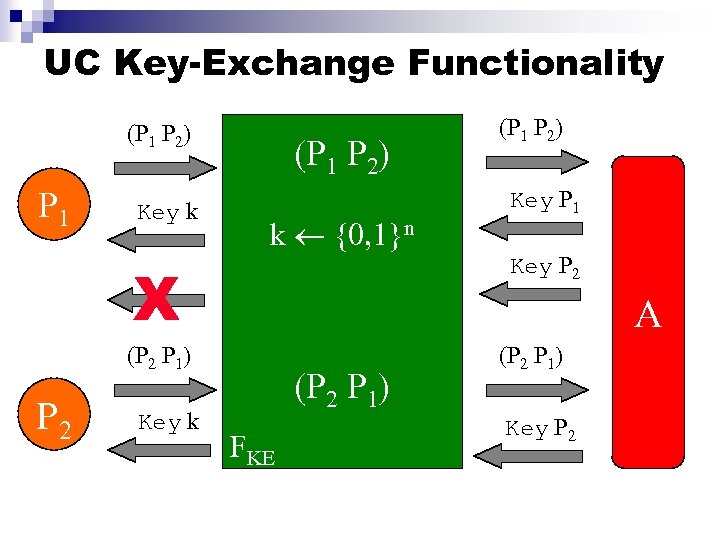
UC Key-Exchange Functionality (P 1 P 2) P 1 Key k (P 1 P 2) k {0, 1}n A (P 2 P 1) Key k Key P 1 Key P 2 X P 2 (P 1 P 2) (P 2 P 1) FKE (P 2 P 1) Key P 2

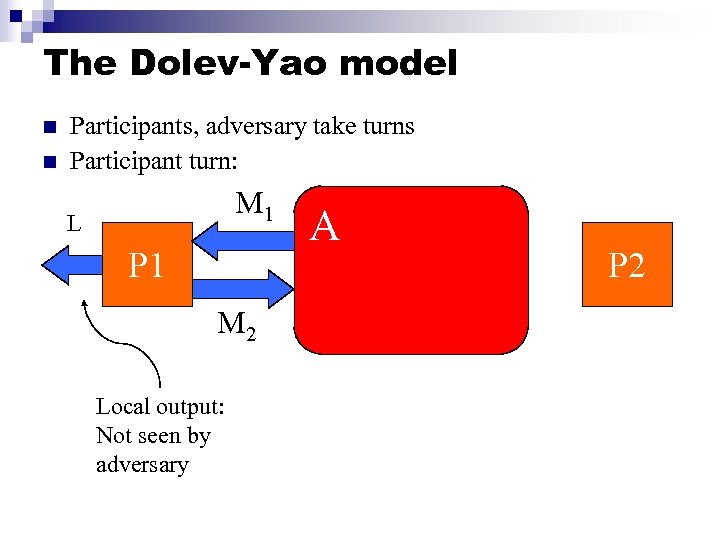
The Dolev-Yao model n n Participants, adversary take turns Participant turn: M 1 L P 1 M 2 Local output: Not seen by adversary A P 2

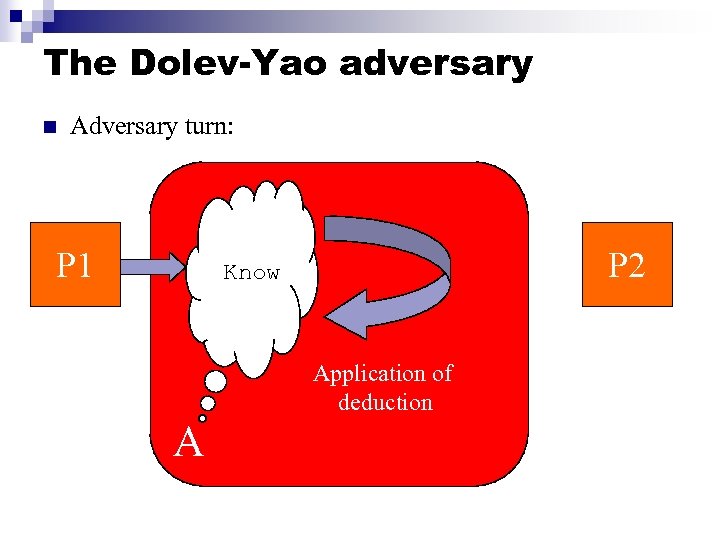
The Dolev-Yao adversary n Adversary turn: P 1 P 2 Know Application of deduction A

Dolev-Yao adversary powers Already in Know M 1, M 2 Pair(M 1, M 2) M, K Enc(M, K), K-1 Always in Know: Randomness generated by adversary Private keys generated by adversary All public keys Can add to Know Pair(M 1, M 2) M 1 and M 2 Enc(M, K) M

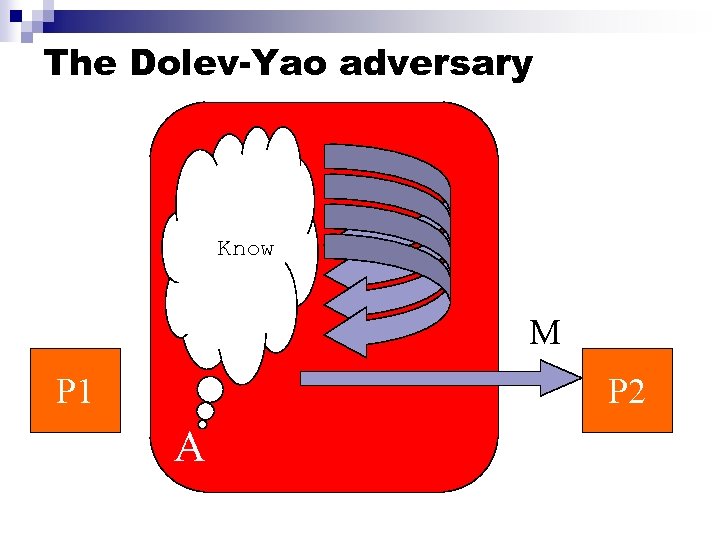
The Dolev-Yao adversary Know M P 1 P 2 A

Dolev-Yao key exchange n Assume that last step of (successful) protocol execution is local output of (Finished Pi Pj K) 1. 2. n Key Agreement: If P 1 outputs (Finished P 1 P 2 K) and P 2 outputs (Finished P 2 P 1 K’) then K = K’. Traditional Dolev-Yao secrecy: If Pi outputs (Finished Pi Pj K), then K can never be in adversary’s set Know Not enough!

Goal of the environment n n n Recall that the environment Z sees outputs of participants Goal: distinguish real protocol from simulation In protocol execution, output of participants (session key) related to protocol messages In ideal world, output independent of simulated protocol If there exists a detectable relationship between session key and protocol messages, environment can distinguish • • • Example: last message of protocol is {“confirm”}K where K is session key Can decrypt with participant output from real protocol Can’t in simulated protocol

Real-or-random (1/3) n n n Need: real-or-random property for session keys • • • Can think of traditional goal as “computational” Need a stronger “decisional” goal Expressed in Dolev-Yao framework Let be a protocol Let r be , except that when participant outputs (Finished Pi Pj Kr), Kr added to Know Let f be , except that when any participant outputs (Finished Pi Pj Kr), fresh key Kf added to adversary set Know Want: adversary can’t distinguish two protocols

Real-or-random (2/3) n n Attempt 1: Let Traces( ) be traces adversary can induce on . Then: Traces( r) = Traces( f) Problem: Kf not in any traces of r Attempt 2: Traces( r) = Rename(Traces( f), Kf Kr) Problem: Two different traces may “look” the same • • Example protocol: If participant receives session key, encrypts “yes” under own (secret) key. Otherwise, encrypts “no” instead Traces different, but adversary can’t tell

Real-or-random (3/3) n n Observable part of trace: Abadi-Rogaway pattern • Undecipherable encryptions replaced by “blob” Example: t = {N 1, N 2}K 1, {N 2}K 2, K 1 -1 Pattern(t) = {N 1, N 2}K 1, K 2, K 1 -1 n Final condition: Pattern(Traces( r)) = Pattern(Rename(Traces( f), Kf Kr)))

Main results n n Let key-exchange in the Dolev-Yao model be: • • • Key agreement Traditional Dolev-Yao secrecy of session key Real-or-random Let be a simple protocol that uses UC asymmetric encryption. Then: DY( ) satisfies Dolev-Yao key exchange iff UC( ) securely realizes FKE

Future work n n n How to prove Dolev-Yao real-or-random? • Needed for UC security • Not previously considered in the Dolev-Yao literature • Can it be automated? Weaker forms of DY real-or-random Similar results for symmetric encryption and signatures