Universal Re-encryption For Mix-Nets and Other Applications to

Universal Re-encryption: For Mix-Nets and Other Applications (to appear CT-RSA ’ 04) Philippe Golle Stanford (now at PARC) Markus Jakobsson Ari Juels RSA Labs UMBC Protocol Meeting 10/01/03 Paul Syverson NRL

Extra Acknowledgements • • • Most Mix illustrations cribbed from a talk by Ari Juels Some RFID slides cribbed from Markus Jakobsson’s ACM Wi. Se’ 03 talk See their Web pages for originals

Talk Outline • • • Background and Motivation for mixes and universal re-encryption Definitions, Security Properties Implementation using El. Gamal Applications: Bulletin Board, RFID Privacy Security Arguments

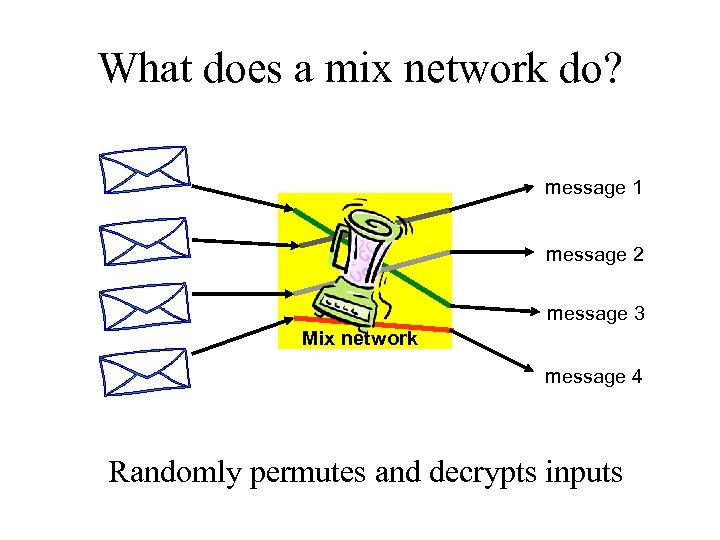What does a mix network do? message 1 message 2 message 3 Mix network message 4 Randomly permutes and decrypts inputs

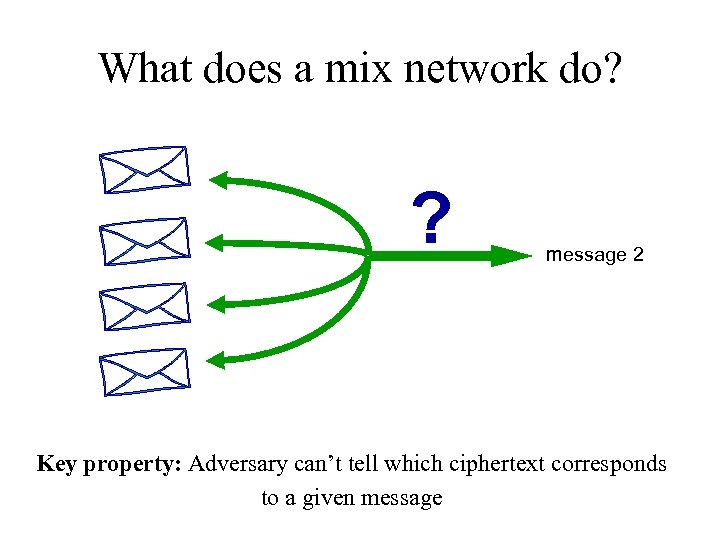What does a mix network do? ? message 2 Key property: Adversary can’t tell which ciphertext corresponds to a given message

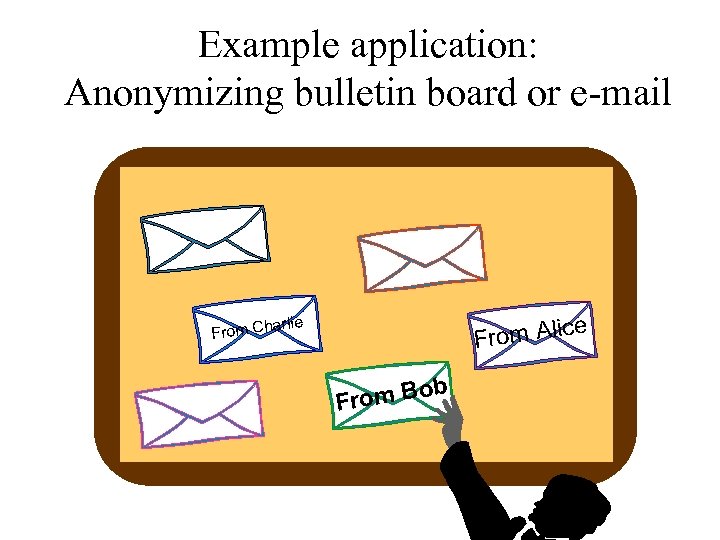Example application: Anonymizing bulletin board or e-mail ce arlie From Ali From Ch om Bob Fr

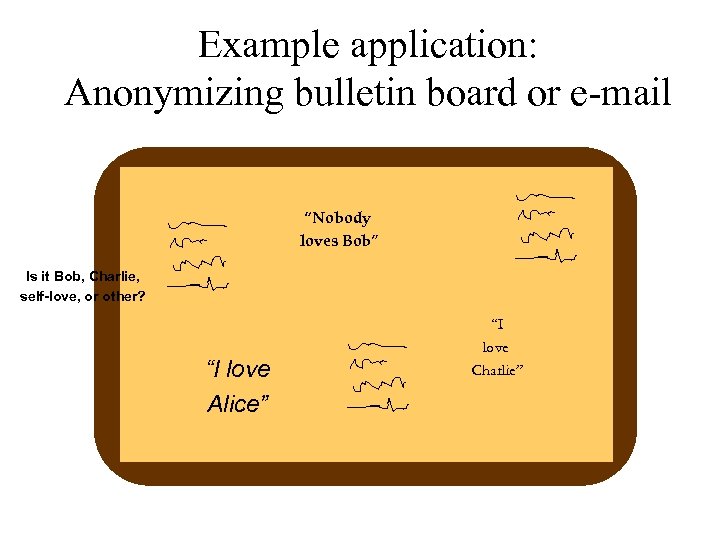Example application: Anonymizing bulletin board or e-mail “Nobody loves Bob” Is it Bob, Charlie, self-love, or other? arlie From Ch “I love Alice” om Bob Fr “I From love Charlie” Alice

A look under the hood

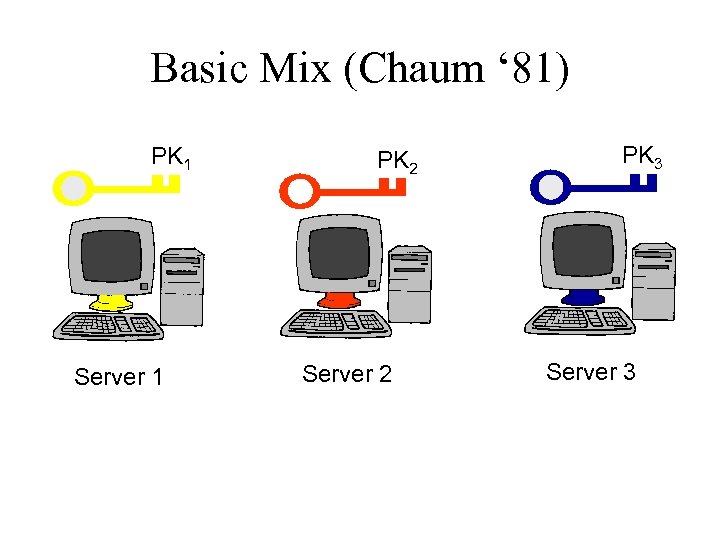Basic Mix (Chaum ‘ 81) PK 1 Server 1 PK 2 Server 2 PK 3 Server 3

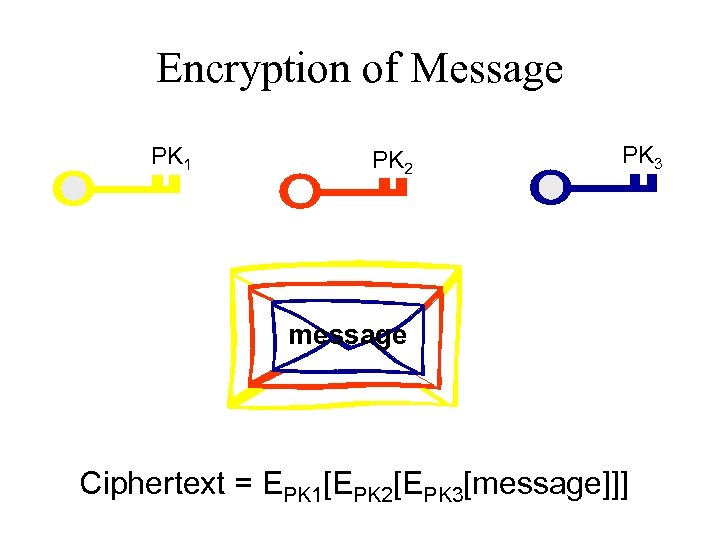Encryption of Message PK 1 PK 2 PK 3 message Ciphertext = EPK 1[EPK 2[EPK 3[message]]]

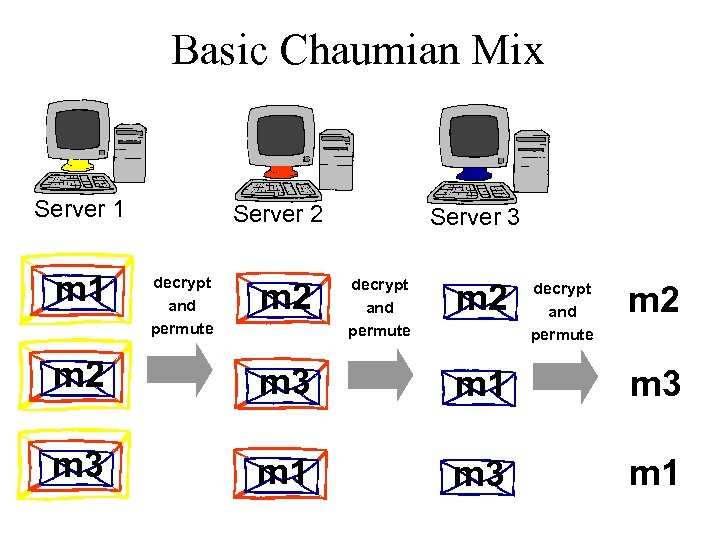Basic Chaumian Mix Server 1 m 1 Server 2 decrypt and permute m 2 Server 3 decrypt and permute m 2 m 2 m 3 m 1

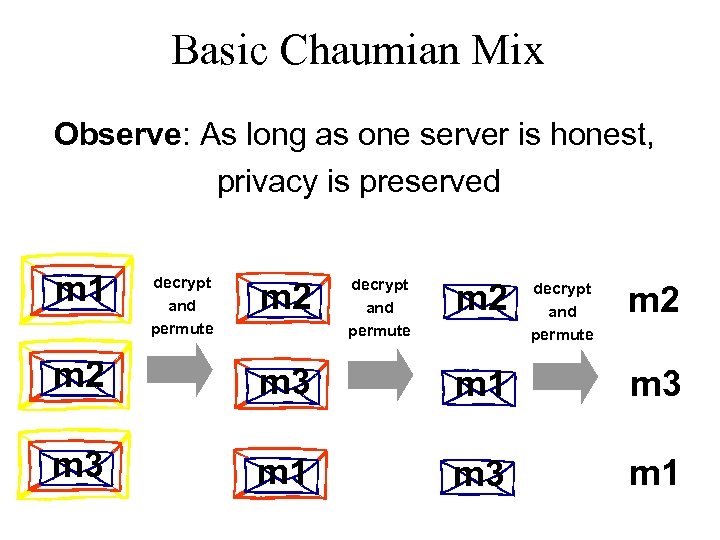Basic Chaumian Mix Observe: As long as one server is honest, privacy is preserved m 1 decrypt and permute m 2 m 3 m 1

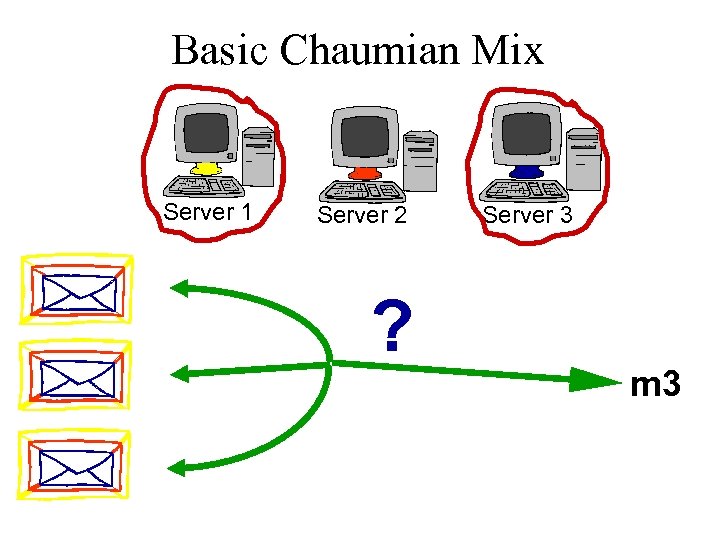Basic Chaumian Mix Server 1 Server 2 ? Server 3 m 3

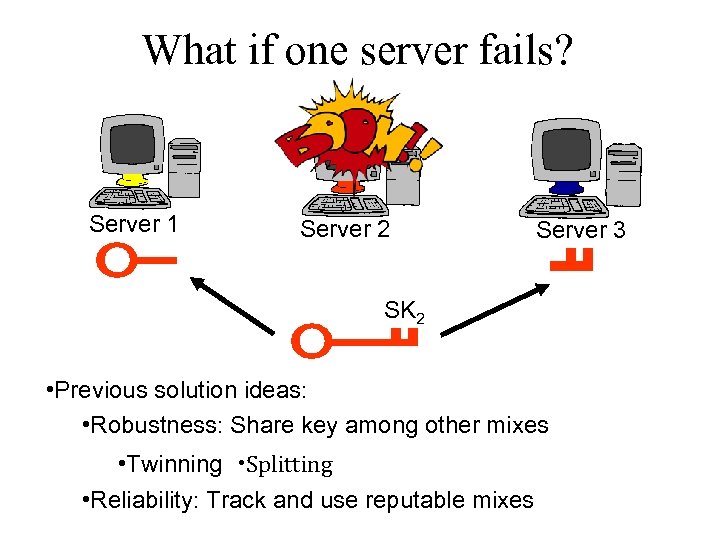What if one server fails? Server 1 Server 2 Server 3 SK 2 • Previous solution ideas: • Robustness: Share key among other mixes • Twinning Splitting • Reliability: Track and use reputable mixes

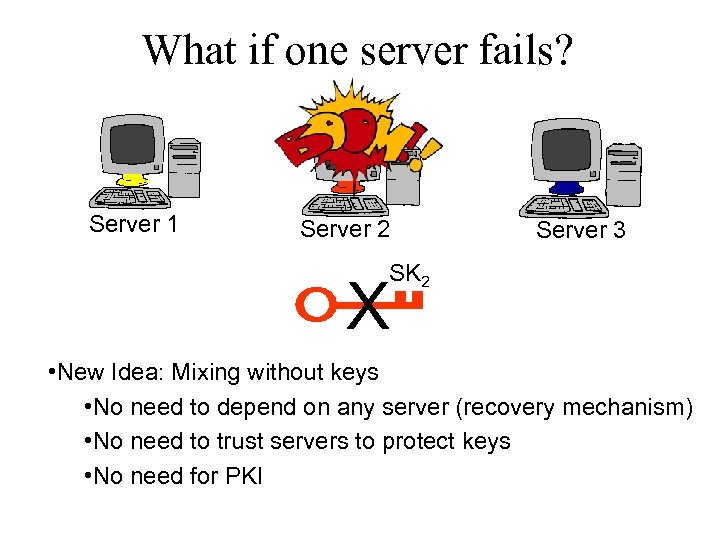What if one server fails? Server 1 Server 2 Server 3 SK 2 X • New Idea: Mixing without keys • No need to depend on any server (recovery mechanism) • No need to trust servers to protect keys • No need for PKI

A look further under the hood

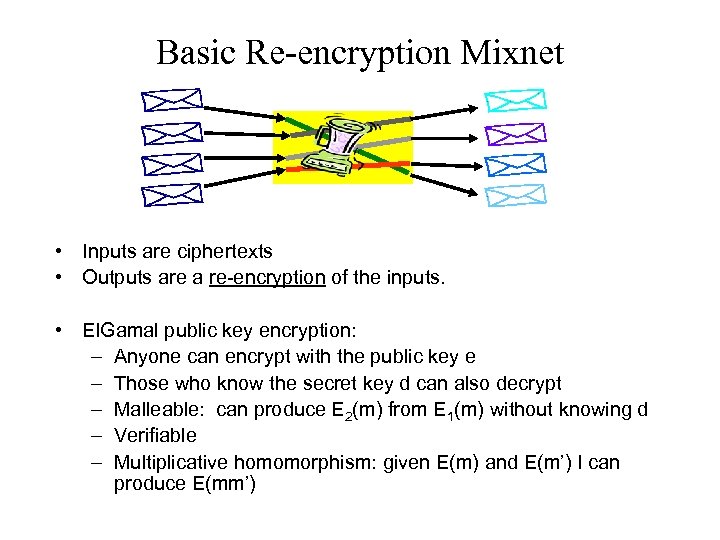Basic Re-encryption Mixnet • Inputs are ciphertexts • Outputs are a re-encryption of the inputs. • El. Gamal public key encryption: – Anyone can encrypt with the public key e – Those who know the secret key d can also decrypt – Malleable: can produce E 2(m) from E 1(m) without knowing d – Verifiable – Multiplicative homomorphism: given E(m) and E(m’) I can produce E(mm’)

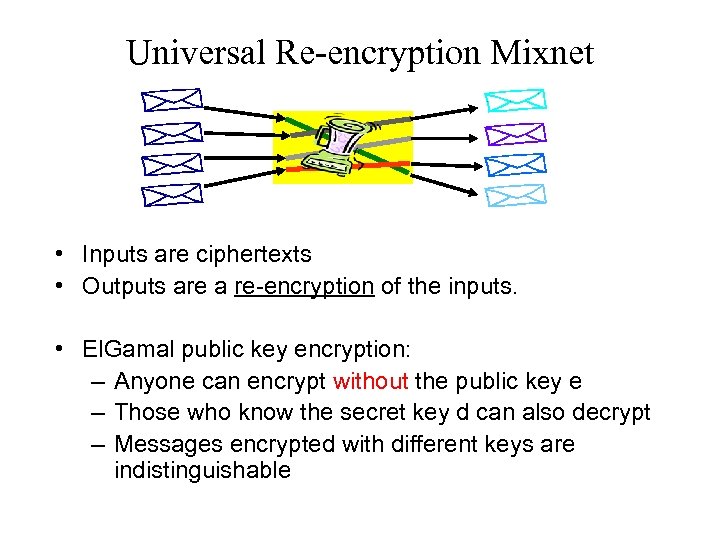Universal Re-encryption Mixnet • Inputs are ciphertexts • Outputs are a re-encryption of the inputs. • El. Gamal public key encryption: – Anyone can encrypt without the public key e – Those who know the secret key d can also decrypt – Messages encrypted with different keys are indistinguishable

Talk Outline • • • Background and Motivation for mixes and universal re-encryption Definitions, Security Properties Implementation using El. Gamal Applications: Bulletin Board, RFID Privacy Security Arguments

Randomized Public-Key Cryptosystem • • • (PK, SK) KG : generate key pairs C E(m, r, PK) : encryption of m m D(SK, C) : decryption of C

Semantic Security • • Adversary chooses (m 0 , m 1 ) Messages are encrypted (C 0 , C 1 ) = (E(m 0, r 0, PK), E(m 1, r 1, PK)) and randomly permuted If adversary determines order correctly no better than by guessing (within ) system is semantically secure

Re-encryption • Given: • Randomized public-key cryptosystem • Ciphertexts of form C = E(m, r, PK) • C’ Re(C, r’, PK) : Re-encryption of m

Semantic Security under Re-encryption • • Adversary chooses (C 0 , C 1 ) Messages are re-encrypted (C 0’, C 1’ ) = (Re(C 0, r 0’, PK), Re(C 1, r 1’, PK)) and randomly permuted If adversary gets order correct no better than by guessing (within ) system is semantically secure under re-encryption

Key-Privacy (Anonymity) • • Adversary chooses message m m is encrypted under PK 0 and PK 1 E(m, PK 0 ) = C 0 E(m, PK 1 ) = C 1 If adversary guesses correspondence of ciphertext with public key with negligible advantage, scheme satisfies key-privacy Bellare et al. (ASIACRYPT’ 01) showed El. Gamal provides anonymity under chosenciphertext assuming DDH.

Universal Re-encryption • Given: • Randomized public-key cryptosystem • Ciphertexts of form C = E(m, r, PK) • X C’ URe(C, r’, PK) : Universal re-encryption of m

Universal Semantic Security under Re-encryption 1. 2. • • • Combines semantic security and key-privacy Given PK 0 and PK 1 adversary chooses (m 0, m 1, r 0, r 1 ) to produce (C 0, C 1 ) Messages are universal re-encrypted (C 0’, C 1’ ) = (URe(C 0, r 0’), URe(C 1, r 1’)) Ciphertexts are randomly ordered (Cb’, C 1 -b’ ) If adversary gets order correct no better than by guessing (within ) system is universal semantically secure under re-encryption

Talk Outline • • • Background and Motivation for mixes and universal re-encryption Definitions, Security Properties El. Gamal based Universal Re-encryption Applications: Bulletin Board, RFID Privacy Security Arguments

El. Gamal Encryption • • P, Q are prime, P = 2 Q + 1 GQ subgroup of ZP* of order Q g generator of GQ x GQ is private key y = gx mod P is public key E(m) = (gr, myr) where r GQ , r random D(G, M) = M/Gx = myr /gxr = m

El. Gamal with Re-encryption • • Ciphertext (G, M) Re-encryption (G’, M’) = (Ggr’, Myr’) • Needs public key y but not private key • • • D(G’, M’) = M’/G’x = myrr’ /gxrr’ = m Introduced for voting Much work on efficient provable shuffles

Universal Re-encryption • • (a, b) = (E[m]; E[1]) E is El. Gamal enc (a’, b’) = (R[b, k]a; R[b, k ’]) • R[*, k] is re-encryption with random k (E[m]’, E[1]’)= ([(myr ykr’, gr gkr’), (yr’k’, gr’k’)] D(E[m]’) = M’/G’x = mykrr’ /gxkrr’ = m

Symmetric-hybrid Encryption U[k 1], U[1], e[k 1, m] • U[1] is universal blank can be converted to U[mi] can be reused • e[k 1, m] is symmetric encryption of m • Final message U[k 1], U[k 2], …U[kn], e[kn-1, …e[k 1, m]…] • Can also do an asymmetric hybrid •

Talk Outline • • • Background and Motivation for mixes and universal re-encryption Definitions, Security Properties Implementation using El. Gamal Applications: Low Volume Bulletin Board, RFID Privacy Security Arguments

Universal Mixnet (Bulletin Board) • Senders post messages universally encrypted for recipients • Proof of Knowledge if nonmalleability desired • Any server can download, mix, and repost any or all messages • • Servers can be dynamic Shuffle proof if desired No PKI and less trust of each server No robustness/reliability issues with server failure • No overhead or threats from replay (universal semantic security)

Low Volume Bulletin Board • • Suppose a bulletin board as above Can mix with previous messages on board Advantage: less delay retrieving new posts Advantage: no need to detect replay (sort of) • Disadvantage: Must try decrypting all messages to find ones for you • Mitigate growth with message removal after Po. K?

RFID Tags • EZ Pass automated toll payment • Supermarket shipment tracking, stock monitoring, theft prevention • Consumer stock monitoring, ordering • Consumer theft-protection of belongings • Implants in family pets • Monitoring cash flows (500 Euro notes)

Privacy Problems

Privacy Solutions?

Privacy Solutions?

Privacy Solutions? Method 2: “Put to sleep” RFID tags Problems: • No continuous use • Complexity, key management, trust

Privacy Solution: Blocker Tags (Juels, Rivest & Szydlo)

Universal Re-encryption for RFID Tag Privacy (Example) • Alice at supermarket checkout. • Uses PKAlice from fidelity card. • Cashier creates universal ciphertexts on Alice’s purchase IDs. • As Alice walks home passes readers that reencrypt her tags or does it herself. • Alice enters home, tags decrypted for home use.

Security of El. Gamal based BB • Correctness: Can do shuffle proofs of correct mixing • Communication privacy: If the universal cryptosystem is universal semantic-secure, then bulletin board construct provides communication privacy. • For El. Gamal implementation, communication privacy reduced to DDH.

Conclusions • Universal Re-encryption: New primitive • Proven Security: • El. Gamal BB is correct (wrt mixing) • El. Gamal BB reducible to DDH. • Applications: • Reduced trust in mixes • Less complex mixnets (no PKI) • Privacy preserving RFID tags • Future • Reduce receiver overhead in bulletin board • Meteor Mixing (with George Danezis)