c0d5d4fefab874e22f77e5aae16d15a5.ppt
- Количество слайдов: 60
 Units of Measurement Dr. David G. Simpson Science Data Processing Branch / Geospace Physics Laboratory Code 587 / 673 February 12, 2013 Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 1
Units of Measurement Dr. David G. Simpson Science Data Processing Branch / Geospace Physics Laboratory Code 587 / 673 February 12, 2013 Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 1
 Introduction Units of measure a fundamental part of science: they connect the physical world to the mathematical world. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 2
Introduction Units of measure a fundamental part of science: they connect the physical world to the mathematical world. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 2
 A Question Which is bigger: a quart of milk or a quart of strawberries? Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 3
A Question Which is bigger: a quart of milk or a quart of strawberries? Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 3
 A Question Which is bigger: a quart of milk or a quart of strawberries? Ans. A quart of strawberries. Units can be tricky! Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 4
A Question Which is bigger: a quart of milk or a quart of strawberries? Ans. A quart of strawberries. Units can be tricky! Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 4
 Systems of Units • MKS Units (meter-kilogram-second) – SI • CGS Units (centimeter-gram-second) – – Electrostatic Electromagnetic Gaussian Heaviside-Lorentz • Other Units – – English units Atomic Astronomical Etc. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 5
Systems of Units • MKS Units (meter-kilogram-second) – SI • CGS Units (centimeter-gram-second) – – Electrostatic Electromagnetic Gaussian Heaviside-Lorentz • Other Units – – English units Atomic Astronomical Etc. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 5
 SI Base Units meter kilogram second ampere kelvin mole candela m kg s A K mol cd length mass time electric current temperature amount of substance luminous intensity SI is the only system based on the meter, kilogram, and second (MKS system). Since the ampere is the base electrical unit, this is also sometimes called an MKSA system. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 6
SI Base Units meter kilogram second ampere kelvin mole candela m kg s A K mol cd length mass time electric current temperature amount of substance luminous intensity SI is the only system based on the meter, kilogram, and second (MKS system). Since the ampere is the base electrical unit, this is also sometimes called an MKSA system. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 6
 Meter • Originally defined to be 1/10, 000 the distance between the North Pole and the equator, along a line passing through Paris. • Meter bar • Krypton-86 wavelengths (1960) • Speed of light (1983) Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 7
Meter • Originally defined to be 1/10, 000 the distance between the North Pole and the equator, along a line passing through Paris. • Meter bar • Krypton-86 wavelengths (1960) • Speed of light (1983) Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 7
 Kilogram • • Originally defined as the mass of 1 liter of water at 0°C (later 4°C) Now defined by an artifact: the International Prototype Kilogram (IPK) in Paris US standard is K 20, with a second standard K 4 used as a consistency check. The only SI base unit with a prefix (for historical reasons) The K 4 US standard kilogram. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 8
Kilogram • • Originally defined as the mass of 1 liter of water at 0°C (later 4°C) Now defined by an artifact: the International Prototype Kilogram (IPK) in Paris US standard is K 20, with a second standard K 4 used as a consistency check. The only SI base unit with a prefix (for historical reasons) The K 4 US standard kilogram. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 8
 Second • Originally defined as 1/86, 400 mean solar day. However, the Earth’s rotation is gradually slowing at an irregular rate due to tidal friction. • The current atomic second is kept by cesium clocks • For historical reasons, the current SI second corresponds to the length of the day in 1820. This means that the second is, in a sense, now “too short” to correspond to rotation of the Earth at its current (slower) rate. As a result, we add “leap seconds” to compensate and keep atomic clocks in step with the Earth’s rotation. These are added at irregular intervals (roughly every 18 months, on average). • Leap seconds may be abolished in the future – still under discussion • www. time. gov for official US time. • See Mini-Course #55 for more on time scales Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 9
Second • Originally defined as 1/86, 400 mean solar day. However, the Earth’s rotation is gradually slowing at an irregular rate due to tidal friction. • The current atomic second is kept by cesium clocks • For historical reasons, the current SI second corresponds to the length of the day in 1820. This means that the second is, in a sense, now “too short” to correspond to rotation of the Earth at its current (slower) rate. As a result, we add “leap seconds” to compensate and keep atomic clocks in step with the Earth’s rotation. These are added at irregular intervals (roughly every 18 months, on average). • Leap seconds may be abolished in the future – still under discussion • www. time. gov for official US time. • See Mini-Course #55 for more on time scales Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 9
 Mole • A mole is just 6. 02214129 × 1023 of something • Just as 12 = “dozen” and 20 = “score”, similarly 602, 214, 129, 000, 000 = “mole” • Mole = Avogadro’s number = reciprocal of atomic mass unit (amu), in grams • Usually used to count atoms or molecules; useful for converting mass to number of atoms or molecules • 1 mole of atoms/molecules has a mass (in grams) equal to its atomic/molecular weight • 1 mole is defined as the number of carbon atoms in 12. 0 grams of carbon-12. • moles = grams/(atomic or molecular weight) • The SI unit mole is equivalent to the gram-mole. Several other moles exist: the kilogram-mole, pound-mole, and ounce-mole. • There is about ½ mole of stars in the visible Universe Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 10
Mole • A mole is just 6. 02214129 × 1023 of something • Just as 12 = “dozen” and 20 = “score”, similarly 602, 214, 129, 000, 000 = “mole” • Mole = Avogadro’s number = reciprocal of atomic mass unit (amu), in grams • Usually used to count atoms or molecules; useful for converting mass to number of atoms or molecules • 1 mole of atoms/molecules has a mass (in grams) equal to its atomic/molecular weight • 1 mole is defined as the number of carbon atoms in 12. 0 grams of carbon-12. • moles = grams/(atomic or molecular weight) • The SI unit mole is equivalent to the gram-mole. Several other moles exist: the kilogram-mole, pound-mole, and ounce-mole. • There is about ½ mole of stars in the visible Universe Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 10
 Kelvin The SI unit for temperature. Kelvin is an absolute scale: 0 K = absolute zero. The temperature interval (the “size” of a degree) is the same in both the Celsius and kelvin scales. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 11
Kelvin The SI unit for temperature. Kelvin is an absolute scale: 0 K = absolute zero. The temperature interval (the “size” of a degree) is the same in both the Celsius and kelvin scales. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 11
 Ampere The ampere is the base electromagnetic unit. Defined as the current necessary in two parallel wires separated by 1 meter to have e force per unit length of 2× 10 -7 N/m Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 12
Ampere The ampere is the base electromagnetic unit. Defined as the current necessary in two parallel wires separated by 1 meter to have e force per unit length of 2× 10 -7 N/m Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 12
 Candela Essentially the same as the older unit “candlepower” – at one time was defined as the light emitted by a standard candle of standard composition. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 13
Candela Essentially the same as the older unit “candlepower” – at one time was defined as the light emitted by a standard candle of standard composition. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 13
 Why Seven Base Units? • Seven base units are not necessary; one will do. (E. g. natural units) • Seven is a tradeoff: having fewer base units makes equations simpler; having more base units makes measurements more practical. • SI units may be re-defined in the near future to have zero base units. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 14
Why Seven Base Units? • Seven base units are not necessary; one will do. (E. g. natural units) • Seven is a tradeoff: having fewer base units makes equations simpler; having more base units makes measurements more practical. • SI units may be re-defined in the near future to have zero base units. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 14
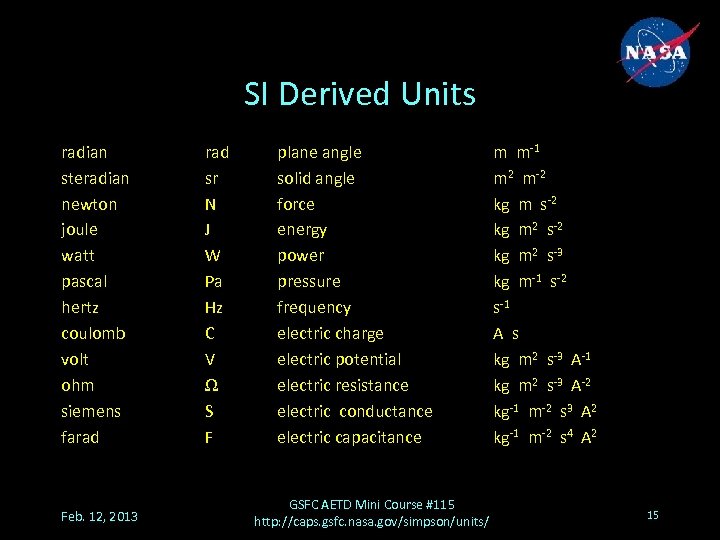 SI Derived Units radian steradian newton joule watt pascal hertz coulomb volt ohm siemens farad Feb. 12, 2013 rad sr N J W Pa Hz C V Ω S F plane angle solid angle force energy power pressure frequency electric charge electric potential electric resistance electric conductance electric capacitance GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ m m-1 m 2 m-2 kg m s-2 kg m 2 s-3 kg m-1 s-2 s-1 A s kg m 2 s-3 A-1 kg m 2 s-3 A-2 kg-1 m-2 s 3 A 2 kg-1 m-2 s 4 A 2 15
SI Derived Units radian steradian newton joule watt pascal hertz coulomb volt ohm siemens farad Feb. 12, 2013 rad sr N J W Pa Hz C V Ω S F plane angle solid angle force energy power pressure frequency electric charge electric potential electric resistance electric conductance electric capacitance GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ m m-1 m 2 m-2 kg m s-2 kg m 2 s-3 kg m-1 s-2 s-1 A s kg m 2 s-3 A-1 kg m 2 s-3 A-2 kg-1 m-2 s 3 A 2 kg-1 m-2 s 4 A 2 15
 SI Derived Units weber tesla henry lumen lux becquerel gray sievert katal Feb. 12, 2013 Wb T H lm lx Bq Gy Sv kat magnetic flux magnetic induction inductance luminous flux illuminance radioactivity absorbed dose equivalent catalytic activity kg m 2 s-2 A-1 kg m 2 s-2 A-2 cd sr m-2 s-1 m 2 s-2 mol s-1 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 16
SI Derived Units weber tesla henry lumen lux becquerel gray sievert katal Feb. 12, 2013 Wb T H lm lx Bq Gy Sv kat magnetic flux magnetic induction inductance luminous flux illuminance radioactivity absorbed dose equivalent catalytic activity kg m 2 s-2 A-1 kg m 2 s-2 A-2 cd sr m-2 s-1 m 2 s-2 mol s-1 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 16
 Photometric Units Photometric units measure the brightness of visible light – electromagnetic radiation weighted by wavelength according to the sensitivity of the human eye at each wavelength. • Lumen (lm) – measures the total light output from a source. • Candela (cd) – measures the total light output per unit solid angle. The candela is essentially the same as the older unit candlepower. • Lux (lx) – measures local illumination level. A typical office is at ~400 lux, while direct sunlight is ~100, 000 lux. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 17
Photometric Units Photometric units measure the brightness of visible light – electromagnetic radiation weighted by wavelength according to the sensitivity of the human eye at each wavelength. • Lumen (lm) – measures the total light output from a source. • Candela (cd) – measures the total light output per unit solid angle. The candela is essentially the same as the older unit candlepower. • Lux (lx) – measures local illumination level. A typical office is at ~400 lux, while direct sunlight is ~100, 000 lux. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 17
 Radiation Units • Becquerel (Bq) – number of radioactive decays per second. • Gray (Gy) – measures absorbed dose: the amount of ionizing radiation energy absorbed per unit mass of material. 1 gray = 100 rads. • Sievert (Sv) – measures dose equivalent, which measures the biological effect of radiation. Sieverts = grays × Q, where Q is a dimensionless quality factor that depends on the type of radiation. 1 sievert = 100 rems. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 18
Radiation Units • Becquerel (Bq) – number of radioactive decays per second. • Gray (Gy) – measures absorbed dose: the amount of ionizing radiation energy absorbed per unit mass of material. 1 gray = 100 rads. • Sievert (Sv) – measures dose equivalent, which measures the biological effect of radiation. Sieverts = grays × Q, where Q is a dimensionless quality factor that depends on the type of radiation. 1 sievert = 100 rems. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 18
 Angular Units • Radian: Angle subtended by an arc whose length is equal to the radius of the circle. 1 full circle = 2π radians – 1 radian = 57. 2958° • Degree: 1/360 of a circle, so 1 full circle = 360°, right angle = 90° – – At one time, degrees were subdivided into minutes, seconds, thirds, fourths, etc. – for example (obliquity of the ecliptic at J 2000): 23° 26’ 21” 26’’’ 53’’’’. Nowadays only minutes, seconds, and fractions of a second are used. Degrees = radians × 180/π • Grad: A “metric degree” – 1/400 of a full circle, so 1 full circle = 400 grads, right angle = 100 grads. Grads appear on most calculators, but are seldom used today. • Steradian: Solid angle subtended by a cone whose area is equal to the square of the radius of the circle. 1 whole sphere = 4π steradians = 41, 253 deg 2. – Degrees 2 = steradians × (180/π)2 Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 19
Angular Units • Radian: Angle subtended by an arc whose length is equal to the radius of the circle. 1 full circle = 2π radians – 1 radian = 57. 2958° • Degree: 1/360 of a circle, so 1 full circle = 360°, right angle = 90° – – At one time, degrees were subdivided into minutes, seconds, thirds, fourths, etc. – for example (obliquity of the ecliptic at J 2000): 23° 26’ 21” 26’’’ 53’’’’. Nowadays only minutes, seconds, and fractions of a second are used. Degrees = radians × 180/π • Grad: A “metric degree” – 1/400 of a full circle, so 1 full circle = 400 grads, right angle = 100 grads. Grads appear on most calculators, but are seldom used today. • Steradian: Solid angle subtended by a cone whose area is equal to the square of the radius of the circle. 1 whole sphere = 4π steradians = 41, 253 deg 2. – Degrees 2 = steradians × (180/π)2 Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 19
 Temperature Units Temperature units are unlike any other units, in that a measure of “zero” is not the same on all scales. The most common temperature scales are: • • Fahrenheit (°F) – Water freezes at 32°F, boils at 212°F Rankine (°R) – Intervals the same as Fahrenheit, but with 0°R at absolute zero Celsius (°C) (also called “centigrade”) – Water freezes at 0°C, boils at 100°C Kelvin (K) – Intervals the same as Celsius, but with 0 K at absolute zero The SI unit for temperature is the kelvin. Note that the degree symbol ( ° ) is not used with the kelvin scale. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 20
Temperature Units Temperature units are unlike any other units, in that a measure of “zero” is not the same on all scales. The most common temperature scales are: • • Fahrenheit (°F) – Water freezes at 32°F, boils at 212°F Rankine (°R) – Intervals the same as Fahrenheit, but with 0°R at absolute zero Celsius (°C) (also called “centigrade”) – Water freezes at 0°C, boils at 100°C Kelvin (K) – Intervals the same as Celsius, but with 0 K at absolute zero The SI unit for temperature is the kelvin. Note that the degree symbol ( ° ) is not used with the kelvin scale. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 20
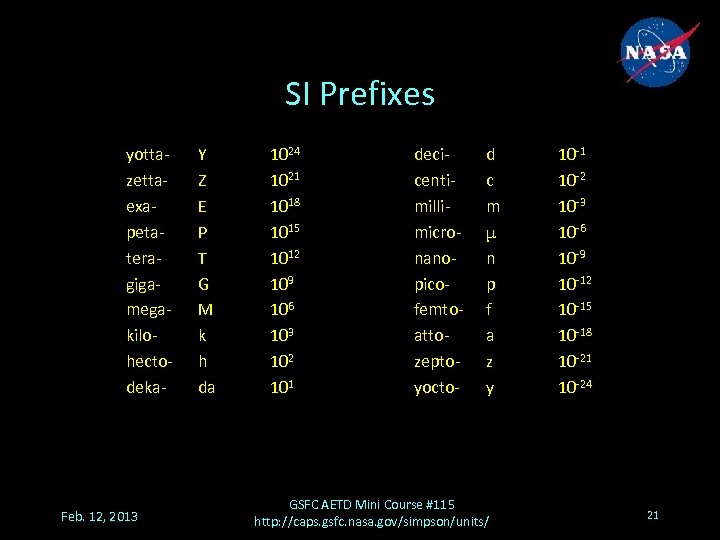 SI Prefixes yottazettaexapetateragigamegakilohectodeka- Feb. 12, 2013 Y Z E P T G M k h da 1024 1021 1018 1015 1012 109 106 103 102 101 decicentimillimicronanopicofemtoattozeptoyocto- d c m μ n p f a z y GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 10 -1 10 -2 10 -3 10 -6 10 -9 10 -12 10 -15 10 -18 10 -21 10 -24 21
SI Prefixes yottazettaexapetateragigamegakilohectodeka- Feb. 12, 2013 Y Z E P T G M k h da 1024 1021 1018 1015 1012 109 106 103 102 101 decicentimillimicronanopicofemtoattozeptoyocto- d c m μ n p f a z y GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 10 -1 10 -2 10 -3 10 -6 10 -9 10 -12 10 -15 10 -18 10 -21 10 -24 21
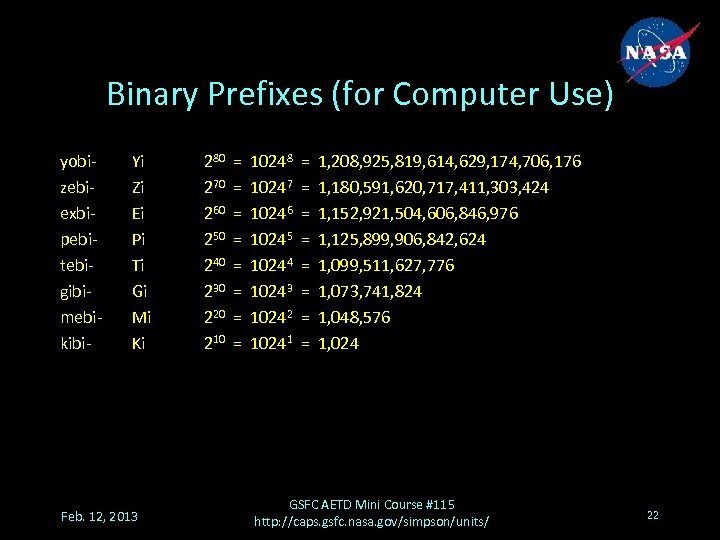 Binary Prefixes (for Computer Use) yobizebiexbipebitebigibimebikibi- Yi Zi Ei Pi Ti Gi Mi Ki Feb. 12, 2013 280 270 260 250 240 230 220 210 = = = = 10248 10247 10246 10245 10244 10243 10242 10241 = = = = 1, 208, 925, 819, 614, 629, 174, 706, 176 1, 180, 591, 620, 717, 411, 303, 424 1, 152, 921, 504, 606, 846, 976 1, 125, 899, 906, 842, 624 1, 099, 511, 627, 776 1, 073, 741, 824 1, 048, 576 1, 024 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 22
Binary Prefixes (for Computer Use) yobizebiexbipebitebigibimebikibi- Yi Zi Ei Pi Ti Gi Mi Ki Feb. 12, 2013 280 270 260 250 240 230 220 210 = = = = 10248 10247 10246 10245 10244 10243 10242 10241 = = = = 1, 208, 925, 819, 614, 629, 174, 706, 176 1, 180, 591, 620, 717, 411, 303, 424 1, 152, 921, 504, 606, 846, 976 1, 125, 899, 906, 842, 624 1, 099, 511, 627, 776 1, 073, 741, 824 1, 048, 576 1, 024 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 22
 Metric Non-SI Units Several units in common use are “metric” units, but not part of the SI system: • Liter (L) = 1 dm 3 (Useful fact: 1 m. L = 1 cm 3) • Temperature in degrees Celsius (°C) Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 23
Metric Non-SI Units Several units in common use are “metric” units, but not part of the SI system: • Liter (L) = 1 dm 3 (Useful fact: 1 m. L = 1 cm 3) • Temperature in degrees Celsius (°C) Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 23
 Unit Conversions 1. 2. Write each conversion factor as a ratio with units only. The units must cancel so that the final product has the proper units. Fill in numbers in each ratio so that the numerator and denominator both represent the same length, time, etc. Example. Convert 60 miles/hour to feet/second. First fill in known conversion factors (units only): Now fill in the same length or time in both the numerator and denominator. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 24
Unit Conversions 1. 2. Write each conversion factor as a ratio with units only. The units must cancel so that the final product has the proper units. Fill in numbers in each ratio so that the numerator and denominator both represent the same length, time, etc. Example. Convert 60 miles/hour to feet/second. First fill in known conversion factors (units only): Now fill in the same length or time in both the numerator and denominator. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 24
 A More Complicated Example Convert 250, 000 furlongs/fortnight to m/s. Now fill in the same length or time in the numerator and denominator: Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 25
A More Complicated Example Convert 250, 000 furlongs/fortnight to m/s. Now fill in the same length or time in the numerator and denominator: Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 25
 Conversions Involving Powers 2000 cubic feet to (US liquid) gallons. First fill in known conversion factors (units only): Now put the same length or volume in the numerator and denominator: Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 26
Conversions Involving Powers 2000 cubic feet to (US liquid) gallons. First fill in known conversion factors (units only): Now put the same length or volume in the numerator and denominator: Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 26
 Conversions Involving Temperature Be careful when making unit conversions involving temperature. When converting a plain temperature, you must allow for the scale offset. When temperature is part of a compound unit, you use only the interval size. Ex. Convert 68°F to °C. This is just a temperature, so allow for the scale offset: (5/9)(68 – 32) = 20 °C. Ex. Convert 100 J/°F to J/°C. Here temperature is part of a compound unit, so we do not use the offset: just use 1 Celsius degree = 1. 8 Fahrenheit degrees: (100 J/°F) × [1. 8 (F deg)/(C deg)] = 180 J/°C Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 27
Conversions Involving Temperature Be careful when making unit conversions involving temperature. When converting a plain temperature, you must allow for the scale offset. When temperature is part of a compound unit, you use only the interval size. Ex. Convert 68°F to °C. This is just a temperature, so allow for the scale offset: (5/9)(68 – 32) = 20 °C. Ex. Convert 100 J/°F to J/°C. Here temperature is part of a compound unit, so we do not use the offset: just use 1 Celsius degree = 1. 8 Fahrenheit degrees: (100 J/°F) × [1. 8 (F deg)/(C deg)] = 180 J/°C Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 27
 Units as an Error-Checking Method Rules for Units 1. 2. 3. 4. 5. 6. Units on both sides of an equation must match. When adding or subtracting two quantities, they must have the same units. Quantities that appear in exponents must be dimensionless. The argument for functions like sin, cos, tan, arcsin, arccos, arctan, log, and exp must be dimensionless. When checking units, radians and steradians can be considered dimensionless. When checking complicated units, it may be useful to break down all derived units into base units (e. g. replace newtons with kg m s-2). Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 28
Units as an Error-Checking Method Rules for Units 1. 2. 3. 4. 5. 6. Units on both sides of an equation must match. When adding or subtracting two quantities, they must have the same units. Quantities that appear in exponents must be dimensionless. The argument for functions like sin, cos, tan, arcsin, arccos, arctan, log, and exp must be dimensionless. When checking units, radians and steradians can be considered dimensionless. When checking complicated units, it may be useful to break down all derived units into base units (e. g. replace newtons with kg m s-2). Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 28
 Example A circular Wien filter is a device that produces electric and magnetic fields arranged in such a way that only electrons of a certain velocity are able to pass through the device in a straight line. We recently derived an expression for the speed of the undeflected electrons, and found Is this correct? We can check for consistency of units. (Here vφ is in m/s; r, r 0, and d in m; me in kg; q in C; Bθ in T; and Φ 0 in V. ) Breaking everything down to base units (m, kg, s, A), we find Both sides have units of m/s, so at least the units are OK. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 29
Example A circular Wien filter is a device that produces electric and magnetic fields arranged in such a way that only electrons of a certain velocity are able to pass through the device in a straight line. We recently derived an expression for the speed of the undeflected electrons, and found Is this correct? We can check for consistency of units. (Here vφ is in m/s; r, r 0, and d in m; me in kg; q in C; Bθ in T; and Φ 0 in V. ) Breaking everything down to base units (m, kg, s, A), we find Both sides have units of m/s, so at least the units are OK. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 29
 Example An early draft of the Cassini CAPS instrument paper included an equation for the time of flight of negative ions: where the mass M is in amu, Q is charge in C, L is a length in m, Eint is an energy in J, and k is an “effective spring constant” with units of amu C-1 s-2. Problem 1. M must be converted to kg and k to units of kg C-1 s-2 for dimensional consistency. Problem 2. k. L 2 has units of volts, while Eint has units of joules. Solution: both occurrences of Eint should be replaced by Eint /Q. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 30
Example An early draft of the Cassini CAPS instrument paper included an equation for the time of flight of negative ions: where the mass M is in amu, Q is charge in C, L is a length in m, Eint is an energy in J, and k is an “effective spring constant” with units of amu C-1 s-2. Problem 1. M must be converted to kg and k to units of kg C-1 s-2 for dimensional consistency. Problem 2. k. L 2 has units of volts, while Eint has units of joules. Solution: both occurrences of Eint should be replaced by Eint /Q. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 30
 Example An early draft of the Cassini CAPS instrument paper included an equation for the time of flight of positive ions: where the mass M is in amu, Q is charge in C, L is a length in m, Eint is an energy J, and k is an “effective spring constant” with units of amu C-1 s-2. Problem 1. M must be converted to kg and k to units of kg C-1 s-2 for dimensional consistency. Problem 2. The argument of the sin-1 function has units of when it should be dimensionless. (Solution: Eint should be replaced by Eint /Q. ) Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 31
Example An early draft of the Cassini CAPS instrument paper included an equation for the time of flight of positive ions: where the mass M is in amu, Q is charge in C, L is a length in m, Eint is an energy J, and k is an “effective spring constant” with units of amu C-1 s-2. Problem 1. M must be converted to kg and k to units of kg C-1 s-2 for dimensional consistency. Problem 2. The argument of the sin-1 function has units of when it should be dimensionless. (Solution: Eint should be replaced by Eint /Q. ) Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 31
 Rationalized Units A system of units is said to be rationalized if is defined in such a way that factors of 4π are eliminated from Maxwell’s equations. The idea (first suggested by Heaviside in 1882) is to eliminate the “eruption of 4 π’s” in electromagnetic equations that have no spherical or cylindrical symmetry. In un-rationalized units (e. g. electrostatic and electromagnetic), factors of 4π appear in Gauss’s and Ampère’s laws: but they disappear in Coulomb’s law: In rationalized units (e. g. SI and Heaviside-Lorentz), the factors of 4π are absent from Maxwell’s equations, but re-appear in Coulomb’s law. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 32
Rationalized Units A system of units is said to be rationalized if is defined in such a way that factors of 4π are eliminated from Maxwell’s equations. The idea (first suggested by Heaviside in 1882) is to eliminate the “eruption of 4 π’s” in electromagnetic equations that have no spherical or cylindrical symmetry. In un-rationalized units (e. g. electrostatic and electromagnetic), factors of 4π appear in Gauss’s and Ampère’s laws: but they disappear in Coulomb’s law: In rationalized units (e. g. SI and Heaviside-Lorentz), the factors of 4π are absent from Maxwell’s equations, but re-appear in Coulomb’s law. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 32
 MVSA Units Although officially the base units in SI are the m, kg, s, A, K, mol, and cd, it is possible to treat them as if the kilogram is replaced by the volt as a base unit; we may call this “MVSA” units. This method can simplify unit checking by breaking down quantities to a simpler set of base units. For example, in MKSA units, 1 Ω = 1 kg m 2 A-2 s-3. Using the volt instead of the kilogram as a base unit, we have 1 Ω = 1 V A-1. In this system, 1 kg = 1 V A s 3 m-2. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 33
MVSA Units Although officially the base units in SI are the m, kg, s, A, K, mol, and cd, it is possible to treat them as if the kilogram is replaced by the volt as a base unit; we may call this “MVSA” units. This method can simplify unit checking by breaking down quantities to a simpler set of base units. For example, in MKSA units, 1 Ω = 1 kg m 2 A-2 s-3. Using the volt instead of the kilogram as a base unit, we have 1 Ω = 1 V A-1. In this system, 1 kg = 1 V A s 3 m-2. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 33
 CGS Units CGS units have as their base units: • Length in centimeters (cm) • Mass in grams (g) • Time in seconds (s) • No base electrical unit (unlike SI, which has the ampere) Several different CGS systems exist; they differ in how they define electromagnetic quantities: • Electrostatic • Electromagnetic • Gaussian • Heaviside-Lorentz Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 34
CGS Units CGS units have as their base units: • Length in centimeters (cm) • Mass in grams (g) • Time in seconds (s) • No base electrical unit (unlike SI, which has the ampere) Several different CGS systems exist; they differ in how they define electromagnetic quantities: • Electrostatic • Electromagnetic • Gaussian • Heaviside-Lorentz Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 34
 Electrostatic Units Electrostatic units define: • Electric charge in statcoulombs (aka franklins): 1 stat. C = 1 g 1/2 cm 3/2 s-1 • Electric potential in statvolts: 1 stat. V = 1 g 1/2 cm 1/2 s-1 • Magnetic induction (B) in statweber/cm 2: 1 stat. Wb/cm 2 = 1 g 1/2 cm-3/2 • Induction (L) in stathenries: 1 stat. H = 1 s 2 cm-1 Note that expressing electromagnetic units in terms of base units results in grams and centimeters being raised to fractional powers. This is a consequence of CGS systems having no base electrical unit. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 35
Electrostatic Units Electrostatic units define: • Electric charge in statcoulombs (aka franklins): 1 stat. C = 1 g 1/2 cm 3/2 s-1 • Electric potential in statvolts: 1 stat. V = 1 g 1/2 cm 1/2 s-1 • Magnetic induction (B) in statweber/cm 2: 1 stat. Wb/cm 2 = 1 g 1/2 cm-3/2 • Induction (L) in stathenries: 1 stat. H = 1 s 2 cm-1 Note that expressing electromagnetic units in terms of base units results in grams and centimeters being raised to fractional powers. This is a consequence of CGS systems having no base electrical unit. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 35
 Electromagnetic Units Electromagnetic units define: • Electric charge in abcoulombs: 1 ab. C = 1 g 1/2 cm 1/2 • Electric potential in abvolts: 1 ab. V = 1 g 1/2 cm 3/2 s-2 • Magnetic induction (B) in gauss: 1 G = 1 g 1/2 cm-1/2 s-1 • Induction (L) in abhenries: 1 ab. H = 1 cm Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 36
Electromagnetic Units Electromagnetic units define: • Electric charge in abcoulombs: 1 ab. C = 1 g 1/2 cm 1/2 • Electric potential in abvolts: 1 ab. V = 1 g 1/2 cm 3/2 s-2 • Magnetic induction (B) in gauss: 1 G = 1 g 1/2 cm-1/2 s-1 • Induction (L) in abhenries: 1 ab. H = 1 cm Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 36
 Gaussian Units Gaussian units combine the electrical units from the esu system with magnetic units from the emu system. This is the most common cgs system. Gaussian units define: • Electric charge in statcoulombs: 1 stat. C = 1 g 1/2 cm 3/2 s-1 • Electric potential in statvolts: 1 stat. V = 1 g 1/2 cm 1/2 s-1 • Magnetic induction (B) in gauss: 1 G = 1 g 1/2 cm-1/2 s-1 • Induction (L) in stathenries: 1 stat. H = 1 s 2 cm-1 Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 37
Gaussian Units Gaussian units combine the electrical units from the esu system with magnetic units from the emu system. This is the most common cgs system. Gaussian units define: • Electric charge in statcoulombs: 1 stat. C = 1 g 1/2 cm 3/2 s-1 • Electric potential in statvolts: 1 stat. V = 1 g 1/2 cm 1/2 s-1 • Magnetic induction (B) in gauss: 1 G = 1 g 1/2 cm-1/2 s-1 • Induction (L) in stathenries: 1 stat. H = 1 s 2 cm-1 Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 37
 Heaviside-Lorentz Units Heaviside-Lorentz units are rationalized Gaussian units. They differ from their Gaussian counterparts only by factors of 4π or √ 4π. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 38
Heaviside-Lorentz Units Heaviside-Lorentz units are rationalized Gaussian units. They differ from their Gaussian counterparts only by factors of 4π or √ 4π. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 38
 Metric Units that Never Were • Grads – a unit of plane angle, where a right angle is 100 grads instead of 90° • Decimal clock: • Decimal calendar with 10 -day week Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 39
Metric Units that Never Were • Grads – a unit of plane angle, where a right angle is 100 grads instead of 90° • Decimal clock: • Decimal calendar with 10 -day week Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 39
 Pole Strength & Magnetic Moment Two conventions for pole strength and magnetic moment: • B-field convention • H-field convention Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 40
Pole Strength & Magnetic Moment Two conventions for pole strength and magnetic moment: • B-field convention • H-field convention Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 40
 Pole Strength & Magnetic Moment B-Field Convention • Force on a pole q* in a magnetic field B is: F = q* B • SI units of pole strength are A m • Force between two magnetic poles is: • • Feb. 12, 2013 Magnetic moment m = q*ℓ has units of A m 2. Relation to H-field convention: q* = Q* / μ 0. 1 unit pole equiv. to 0. 1 A m 1 pole cm equiv. to 0. 001 A m 2. GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 41
Pole Strength & Magnetic Moment B-Field Convention • Force on a pole q* in a magnetic field B is: F = q* B • SI units of pole strength are A m • Force between two magnetic poles is: • • Feb. 12, 2013 Magnetic moment m = q*ℓ has units of A m 2. Relation to H-field convention: q* = Q* / μ 0. 1 unit pole equiv. to 0. 1 A m 1 pole cm equiv. to 0. 001 A m 2. GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 41
 Pole Strength & Magnetic Moment H-Field Convention • Force on a pole q* in a magnetic field B is: F = Q* H • SI units of pole strength are Wb • Force between two magnetic poles is: • • Feb. 12, 2013 Magnetic moment d = Q*ℓ has units of Wb m. Relation to B-field convention: Q* = μ 0 q*. 1 unit pole = 4π × 10 -8 Wb 1 pole cm = 4π × 10 -10 Wb m GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 42
Pole Strength & Magnetic Moment H-Field Convention • Force on a pole q* in a magnetic field B is: F = Q* H • SI units of pole strength are Wb • Force between two magnetic poles is: • • Feb. 12, 2013 Magnetic moment d = Q*ℓ has units of Wb m. Relation to B-field convention: Q* = μ 0 q*. 1 unit pole = 4π × 10 -8 Wb 1 pole cm = 4π × 10 -10 Wb m GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 42
 Metric Technical Units Base units are: • Meter (length) • Kilogram-force (force); 1 kgf = 9. 80665 N • Second (time) Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 43
Metric Technical Units Base units are: • Meter (length) • Kilogram-force (force); 1 kgf = 9. 80665 N • Second (time) Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 43
 English Units There are three systems of English units. All use the foot as the base unit of length, and the second as the base unit of time. • British Engineering (English Gravitational) Units: • Mass in slugs (1 slug = 32. 17405 lbm) • Force in pounds-force (lbf) • Newton’s 2 nd law: F = ma • English Absolute Units: • Mass in pounds-mass (lbm) • Force in poundals (1 pdl = 0. 031081 lbf) • Newton’s 2 nd law: F = ma • English Engineering Units: • Mass in pounds-mass (lbm) • Force in pounds-force (lbf) • Newton’s 2 nd law: F = (1/β) ma, β = 32. 17405 lbm ft lbf-1 s-2 Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 44
English Units There are three systems of English units. All use the foot as the base unit of length, and the second as the base unit of time. • British Engineering (English Gravitational) Units: • Mass in slugs (1 slug = 32. 17405 lbm) • Force in pounds-force (lbf) • Newton’s 2 nd law: F = ma • English Absolute Units: • Mass in pounds-mass (lbm) • Force in poundals (1 pdl = 0. 031081 lbf) • Newton’s 2 nd law: F = ma • English Engineering Units: • Mass in pounds-mass (lbm) • Force in pounds-force (lbf) • Newton’s 2 nd law: F = (1/β) ma, β = 32. 17405 lbm ft lbf-1 s-2 Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 44
 Avoirdupois Units A system of weights customarily used in civil use in the US. • • 1 grain = 64. 79891 mg = 1/7000 pound 1 dram = 27. 34375 grains = 1. 771845 g = 1/256 pound 1 ounce = 16 drams 1 pound = 16 ounces Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 45
Avoirdupois Units A system of weights customarily used in civil use in the US. • • 1 grain = 64. 79891 mg = 1/7000 pound 1 dram = 27. 34375 grains = 1. 771845 g = 1/256 pound 1 ounce = 16 drams 1 pound = 16 ounces Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 45
 Apothecaries’ Units of mass traditionally used by pharmacists – although metric units are more common nowadays. • • • 1 grain = 64. 79891 grams = 1/5760 apothecaries’ pound 1 apothecaries’ scruple = 20 apothecaries’ grains 1 apothecaries’ dram = 3 apothecaries’ scruples 1 apothecaries’ ounce = 8 apothecaries’ drams 1 apothecaries’ pound = 12 apothecaries’ ounces Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 46
Apothecaries’ Units of mass traditionally used by pharmacists – although metric units are more common nowadays. • • • 1 grain = 64. 79891 grams = 1/5760 apothecaries’ pound 1 apothecaries’ scruple = 20 apothecaries’ grains 1 apothecaries’ dram = 3 apothecaries’ scruples 1 apothecaries’ ounce = 8 apothecaries’ drams 1 apothecaries’ pound = 12 apothecaries’ ounces Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 46
 Troy Units of mass used for precious metals. • 1 troy ounce = 1. 097143 oz avoirdupois = 1 apothecaries’ ounce = 31. 10348 g • 1 troy pound = 12 troy ounces = 1 apothecaries’ pound • 1 troy ton = 2000 troy pounds Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 47
Troy Units of mass used for precious metals. • 1 troy ounce = 1. 097143 oz avoirdupois = 1 apothecaries’ ounce = 31. 10348 g • 1 troy pound = 12 troy ounces = 1 apothecaries’ pound • 1 troy ton = 2000 troy pounds Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 47
 Astronomical Units Used in astronomy. Base units are: • Mass in solar masses • Time in days • Length in units of the Earth-Sun distance The astronomical unit of length was recently re-defined (August 2012 IAU meeting in Peking). Old definition: the radius of an unperturbed circular Newtonian orbit about the Sun of a particle having infinitesimal mass, moving with a mean motion of 0. 01720209895 radians per day (known as the Gaussian constant). New defintion: 1 AU = 149, 597, 870, 700 meters (exactly) Ref. The Astronomical Unit Gets Fixed, Nature News, 14 September 2012, doi: 10. 1038/nature. 2012. 11416 Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 48
Astronomical Units Used in astronomy. Base units are: • Mass in solar masses • Time in days • Length in units of the Earth-Sun distance The astronomical unit of length was recently re-defined (August 2012 IAU meeting in Peking). Old definition: the radius of an unperturbed circular Newtonian orbit about the Sun of a particle having infinitesimal mass, moving with a mean motion of 0. 01720209895 radians per day (known as the Gaussian constant). New defintion: 1 AU = 149, 597, 870, 700 meters (exactly) Ref. The Astronomical Unit Gets Fixed, Nature News, 14 September 2012, doi: 10. 1038/nature. 2012. 11416 Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 48
 Atomic Units Used in atomic physics. Base units are: • Length in Bohr radii: a 0 = 4πε 0ħ 2/mee 2 = 0. 52917721092 × 10 -10 m • Mass in units of electron mass: me = 9. 10938291 × 10 -31 kg • Time is then in units of mea 02 / ħ = 2. 41888 × 10 -17 sec Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 49
Atomic Units Used in atomic physics. Base units are: • Length in Bohr radii: a 0 = 4πε 0ħ 2/mee 2 = 0. 52917721092 × 10 -10 m • Mass in units of electron mass: me = 9. 10938291 × 10 -31 kg • Time is then in units of mea 02 / ħ = 2. 41888 × 10 -17 sec Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 49
 Planck Units Used in theoretical physics; they simplify many equations by setting the physical constants G = ħ = c = 1. Base units are: • Planck length: ℓP = (ħG/c 3)1/2 = 1. 61699 × 10 -35 m • Planck mass: m. P = (ħc/G)1/2 = 2. 17651 × 10 -8 kg • Planck time: t. P = (ħG/c 5)1/2 = 5. 39106 × 10 -44 sec Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 50
Planck Units Used in theoretical physics; they simplify many equations by setting the physical constants G = ħ = c = 1. Base units are: • Planck length: ℓP = (ħG/c 3)1/2 = 1. 61699 × 10 -35 m • Planck mass: m. P = (ħc/G)1/2 = 2. 17651 × 10 -8 kg • Planck time: t. P = (ħG/c 5)1/2 = 5. 39106 × 10 -44 sec Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 50
 Natural Units Used in particle physics; they simplify many equations by setting the physical constants ħ = c = 1. Also, a base energy unit is chosen (typically e. V, Me. V, or Ge. V). All quantities are then expressed in energy units raised to a power. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 51
Natural Units Used in particle physics; they simplify many equations by setting the physical constants ħ = c = 1. Also, a base energy unit is chosen (typically e. V, Me. V, or Ge. V). All quantities are then expressed in energy units raised to a power. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 51
 Currency Units Currency units differ from other units: • Each country has its own currency units. – There was once a proposed international currency unit, the speso, equivalent to 733 μg of gold (about 4¢ at today’s gold prices) • Conversion factors (called exchange rates) are functions of time, varying minute to minute. Bearing this in mind, currency units may be treated like any other unit. Exchange rates: http: //www. xe. com/ucc Keep fluctuations in mind when making overseas procurements. Ex. Gasoline prices: yen per liter to dollars per gallon; dollars per troy oz to dollars per kg Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 52
Currency Units Currency units differ from other units: • Each country has its own currency units. – There was once a proposed international currency unit, the speso, equivalent to 733 μg of gold (about 4¢ at today’s gold prices) • Conversion factors (called exchange rates) are functions of time, varying minute to minute. Bearing this in mind, currency units may be treated like any other unit. Exchange rates: http: //www. xe. com/ucc Keep fluctuations in mind when making overseas procurements. Ex. Gasoline prices: yen per liter to dollars per gallon; dollars per troy oz to dollars per kg Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 52
 Tricky Units • Gallon (US liquid, US dry, imperial); quart, pint – 1 US liquid gal = 231 in 3; 1 US dry gal = 268. 80 in 3; 1 imperial gal = 277. 42 in 3 • Ounce (avoirdupois, troy, apothecaries’, fluid) – – Troy oz is 10% bigger than the avoirdupois oz; troy lb = 12 troy oz Avoirdupois, troy, and apothecaries’ ounce are units of mass; the fluid ounce is a unit of volume • Ton (short, long, troy, metric) – short ton = 2000 lb, long ton = 2240 lb, troy ton = 1645. 714 lb, metric ton = 1000 kg • Foot (international foot, US survey foot) – US survey foot = 1. 000002 ft • “Calorie” – The “calorie” as used in the food industry is 1000 times the “calorie” used in chemistry; it is what chemists would call a “kilocalorie”. – “ 15° calorie” (= 4. 1858 J); “thermochemical calorie” (= 4. 184 J); “international steam table (IT) calorie” (= 4. 1868 J) Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 53
Tricky Units • Gallon (US liquid, US dry, imperial); quart, pint – 1 US liquid gal = 231 in 3; 1 US dry gal = 268. 80 in 3; 1 imperial gal = 277. 42 in 3 • Ounce (avoirdupois, troy, apothecaries’, fluid) – – Troy oz is 10% bigger than the avoirdupois oz; troy lb = 12 troy oz Avoirdupois, troy, and apothecaries’ ounce are units of mass; the fluid ounce is a unit of volume • Ton (short, long, troy, metric) – short ton = 2000 lb, long ton = 2240 lb, troy ton = 1645. 714 lb, metric ton = 1000 kg • Foot (international foot, US survey foot) – US survey foot = 1. 000002 ft • “Calorie” – The “calorie” as used in the food industry is 1000 times the “calorie” used in chemistry; it is what chemists would call a “kilocalorie”. – “ 15° calorie” (= 4. 1858 J); “thermochemical calorie” (= 4. 184 J); “international steam table (IT) calorie” (= 4. 1868 J) Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 53
 The Future of SI Units There is currently a proposal being discussed to eliminate all SI base units by fixing the values of several physical constants : • • Planck’s constant (h) Elementary charge (e) Boltzmann’s constant (k. B) Avogadro’s number (NA) These would re-define the kg, A, K, and mol. The speed of light c has already been fixed in the definition of the meter. This issue has not yet been decided. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 54
The Future of SI Units There is currently a proposal being discussed to eliminate all SI base units by fixing the values of several physical constants : • • Planck’s constant (h) Elementary charge (e) Boltzmann’s constant (k. B) Avogadro’s number (NA) These would re-define the kg, A, K, and mol. The speed of light c has already been fixed in the definition of the meter. This issue has not yet been decided. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 54
 The Future of SI Units Proposed change to SI units would re-define all seven base units; base units would be defined by defining exact values for physical constants: Defined const. Δν(133 Cs)hfs c h e k. B NA Kcd Feb. 12, 2013 Defines the… second meter kilogram ampere kelvin mole candela (Kcd is the luminous efficacy at 540 THz) GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 55
The Future of SI Units Proposed change to SI units would re-define all seven base units; base units would be defined by defining exact values for physical constants: Defined const. Δν(133 Cs)hfs c h e k. B NA Kcd Feb. 12, 2013 Defines the… second meter kilogram ampere kelvin mole candela (Kcd is the luminous efficacy at 540 THz) GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 55
 NASA Case Studies: Flight Software During an earlier GSFC mission, problems were traced to software that modeled the spacecraft and its environment, and was being used to test flight software. There was confusion over whether the modeling software was to produce magnetic field strength in teslas or gauss, and whether magnetic dipole moment was to be in pole-cm or A m 2. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 56
NASA Case Studies: Flight Software During an earlier GSFC mission, problems were traced to software that modeled the spacecraft and its environment, and was being used to test flight software. There was confusion over whether the modeling software was to produce magnetic field strength in teslas or gauss, and whether magnetic dipole moment was to be in pole-cm or A m 2. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 56
 NASA Case Studies: Mars Climate Orbiter • Launched in December 1998 • Reach Mars in September 1999 • Disintegrated in the Martian upper atmosphere. The spacecraft was on an incorrect trajectory due to a units-related error in software used for trajectory models. • A routine to model small forces (SM_FORCES) was to have used thruster performance data (impulse) in N s, but instead lbf s were used. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 57
NASA Case Studies: Mars Climate Orbiter • Launched in December 1998 • Reach Mars in September 1999 • Disintegrated in the Martian upper atmosphere. The spacecraft was on an incorrect trajectory due to a units-related error in software used for trajectory models. • A routine to model small forces (SM_FORCES) was to have used thruster performance data (impulse) in N s, but instead lbf s were used. Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 57
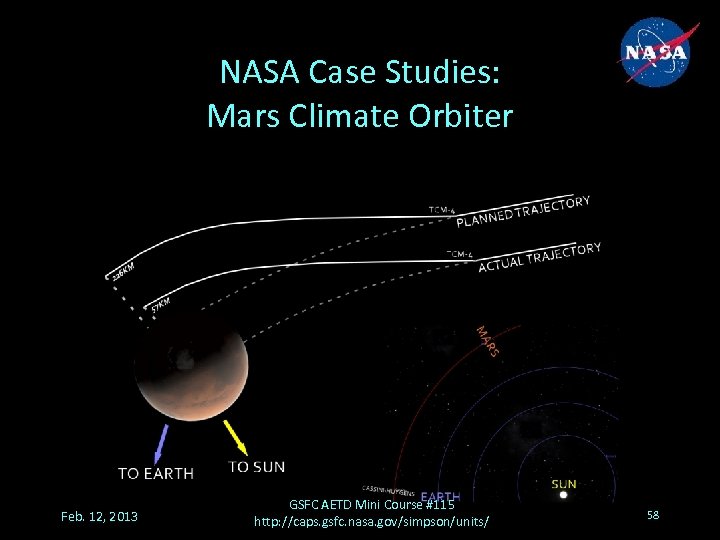 NASA Case Studies: Mars Climate Orbiter Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 58
NASA Case Studies: Mars Climate Orbiter Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 58
 Recommendations • Paying meticulous attention to units of measure can avoid many errors – both in working with equations and in software. • Use units as an error checking technique. • In software, store all variables in memory in a consistent set of units (e. g. SI or Gaussian). If the results are required in different units, perform the unit conversion during output. Angles are usually best stored in radians. • Write comments in software source code to make it clear what units are used at each step. • It is not sufficient to specify that a quantity be given in “metric units” – there are many different metric units! (E. g. magnetic field in gauss or teslas. ) Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 59
Recommendations • Paying meticulous attention to units of measure can avoid many errors – both in working with equations and in software. • Use units as an error checking technique. • In software, store all variables in memory in a consistent set of units (e. g. SI or Gaussian). If the results are required in different units, perform the unit conversion during output. Angles are usually best stored in radians. • Write comments in software source code to make it clear what units are used at each step. • It is not sufficient to specify that a quantity be given in “metric units” – there are many different metric units! (E. g. magnetic field in gauss or teslas. ) Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 59
 Questions? References • Classical Electrodynamics, 2 nd ed. , J. D. Jackson (1975) • Demystifying Electromagnetic Equations: A Complete Explanation of EM Unit Systems and Equation Transformations, Douglas L. Cohen (2001) • Engineering Units and Physical Quantities, H. S. Hvistendahl (1964) • Bureau International des Poids et Mesures (BIPM): www. bipm. org • National Institutes of Standards and Technology (NIST): www. nist. gov/pml/wmd/index. cfm • How Many? A Dictionary of Units of Measurement: www. unc. edu/~rowlett/units/ Course Web site: caps. gsfc. nasa. gov/simpson/units Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 60
Questions? References • Classical Electrodynamics, 2 nd ed. , J. D. Jackson (1975) • Demystifying Electromagnetic Equations: A Complete Explanation of EM Unit Systems and Equation Transformations, Douglas L. Cohen (2001) • Engineering Units and Physical Quantities, H. S. Hvistendahl (1964) • Bureau International des Poids et Mesures (BIPM): www. bipm. org • National Institutes of Standards and Technology (NIST): www. nist. gov/pml/wmd/index. cfm • How Many? A Dictionary of Units of Measurement: www. unc. edu/~rowlett/units/ Course Web site: caps. gsfc. nasa. gov/simpson/units Feb. 12, 2013 GSFC AETD Mini Course #115 http: //caps. gsfc. nasa. gov/simpson/units/ 60


