UNIT-VI Project Management PERT CPM PREPARED BY CH AVINASH

UNIT-VI Project Management (PERT/CPM) PREPARED BY CH. AVINASH

INDEX UNIT 6 PPT SLIDES S. NO. 1. 2. 3. 4. 5. 6. 7. TOPIC Project Management ( PERT/CPM) Network Analysis Programme Evaluation and Review Technique (PERT), Critical Path Method ( CPM ), Identify Critical Path, Probability of Completing the Project Within given time, Project Cost Analysis Project Crashing, (simple problems) LECTURE NO. L 1 L 2 L 3 L 4 L 5 L 6 L 7

Project Planning • Given: – Statement of work • written description of goals • work & time frame of project – Work Breakdown Structure • Be able to: develop precedence relationship diagram which shows sequential relationship of project activities 3

Gantt Chart • Popular tool for project scheduling • Graph with bar representing time for each task • Provides visual display of project schedule • Also shows slack for activities – (amount of time activity can be delayed without delaying project) 4

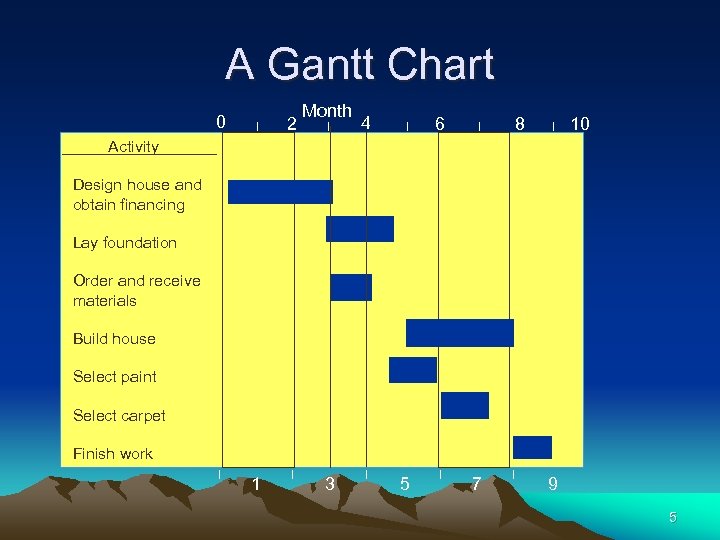
A Gantt Chart 0 ½ 2 Month ½ 4 ½ 6 ½ 8 ½ 10 Activity Design house and obtain financing Lay foundation Order and receive materials Build house Select paint Select carpet Finish work ½ 1 ½ 3 ½ 5 ½ 7 ½ 9 5

CPM/PERT • Critical Path Method (CPM) – - Du. Pont & Remington-Rand (1956) – - deterministic task times – - activity-on-node network construction (AON) • Project Evaluation & Review Technique (PERT) – - U. S. Navy, Booz, Allen & Hamilton – - multiple task time estimates( probabilistic) – - activity-on-arrow network construction (AOA) 6

Network Construction • In AON, nodes represent activities & arrows show precedence relationships • In AOA, arrows represent activities & nodes are events for points in time • An event is the completion or beginning of an activity • A dummy shows precedence for two activities with same start & end nodes 7

The Project Network consists of branches & nodes Node 1 2 3 Branch 8

Simplified Project Network 1 Construct forms 2 Pour concrete 3 9

Consider the following table which describes the activities to be done to build a house and its sequence Activity predecessors Duration A Design house and obtain financing 3 B Lay foundation A 2 C Order and receive materials A 1 D Build house B, C 3 E Select paint B, C 1 F Select carpet E 1 G Finish work D, F 1 10

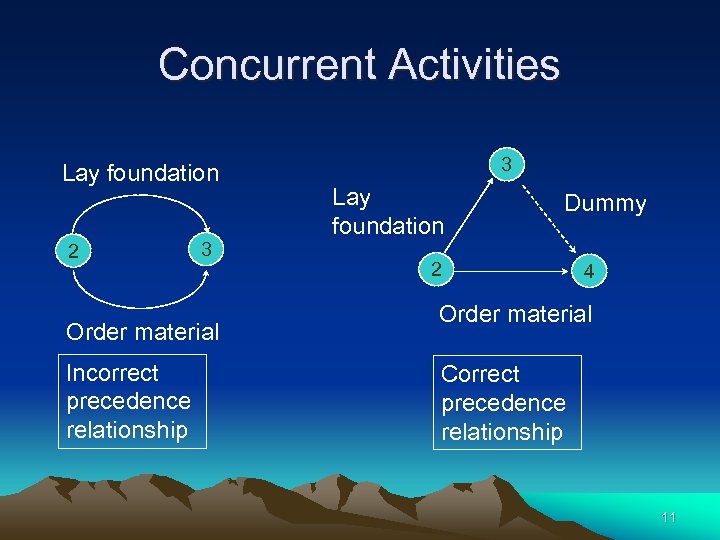
Concurrent Activities Lay foundation 2 3 Order material Incorrect precedence relationship 3 Lay foundation Dummy 2 4 Order material Correct precedence relationship 11

Project Network For A House 3 Lay foundation 1 3 Design house and obtain financing 2 2 0 1 Order and receive materials Dummy 4 Select paint Build house 1 3 5 6 Finish work 1 7 1 Select carpet 12

Critical Path • A path is a sequence of connected activities running from the start to the end node in a network • The critical path is the path with the longest duration in the network • A project cannot be completed in less than the time of the critical path (under normal circumstances) 13

All Possible Paths path 1: 1 -2 -3 -4 -6 -7 3 + 2 + 0 + 3 + 1 = 9 months; the critical path 2: 1 -2 -3 -4 -5 -6 -7 3 + 2 + 0 + 1 + 1 = 8 months path 3: 1 -2 -4 -6 -7 3 + 1 + 3 + 1 = 8 months path 4: 1 -2 -4 -5 -6 -7 3 + 1 + 1 = 7 months 14

Early Times (House building example) • ES - earliest time activity can start • Forward pass starts at beginning of network to determine ES times • EF = ES + activity time – ESij = maximum (EFi) i – EFij = ESij + tij – ES 12 = 0 – EF 12 = ES 12 + t 12 = 0 + 3 = 3 months j 15

Computing Early Times -ES 23 = max (EF 2) = 3 months - ES 46 = max (EF 4) = max (5, 4) = 5 months - EF 46 = ES 46 + t 46 = 5 + 3 = 8 months - EF 67 =9 months, the project duration 16

Late Times • LS - latest time activity can be started without delaying the project • Backward pass starts at end of network to determine LS times • LF - latest time activity can be completed without delaying the project – LSij = LFij - tij – LFij = minimum (LSj) 17

Computing Late Times – If a deadline is not given take LF of the project to be EF of the last activity – LF 67 = 9 months – LS 67 = LF 67 - t 67 = 9 - 1 = 8 months – LF 56 = minimum (LS 6) = 8 months – LS 56 = LF 56 - t 56 = 8 - 1 = 7 months – LF 24 = minimum (LS 4) = min(5, 6) = 5 months – LS 24 = LF 24 - t 24 = 5 - 1 = 4 months 18

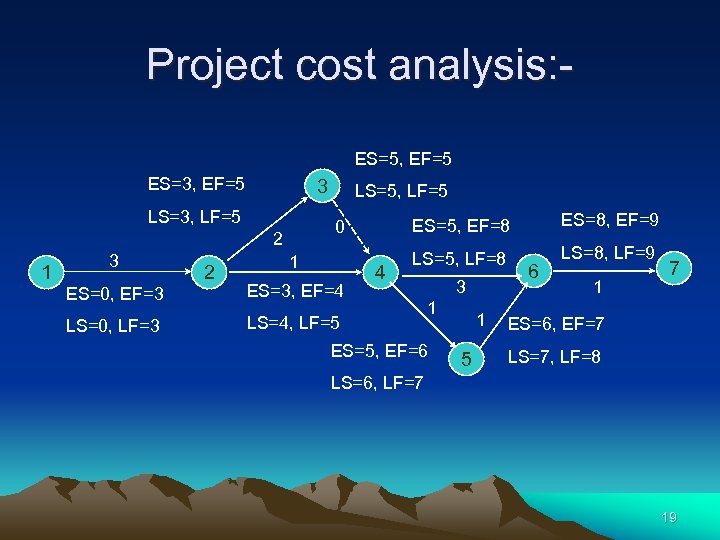
Project cost analysis: ES=5, EF=5 ES=3, EF=5 LS=3, LF=5 1 3 ES=0, EF=3 LS=0, LF=3 2 LS=5, LF=5 ES=5, EF=8 0 1 ES=3, EF=4 4 ES=8, EF=9 LS=5, LF=8 LS=8, LF=9 LS=4, LF=5 1 ES=5, EF=6 LS=6, LF=7 3 1 5 6 1 7 ES=6, EF=7 LS=7, LF=8 19

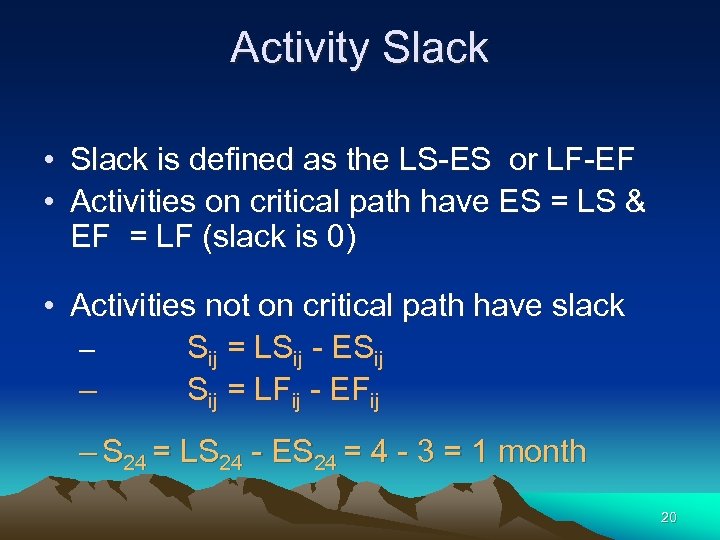
Activity Slack • Slack is defined as the LS-ES or LF-EF • Activities on critical path have ES = LS & EF = LF (slack is 0) • Activities not on critical path have slack – Sij = LSij - ESij – Sij = LFij - EFij – S 24 = LS 24 - ES 24 = 4 - 3 = 1 month 20

Total slack/float or Slack of an activity • Total slack/ float means the amount of time that an activity can be delayed without affecting the entire project completion time. • The activity on a given path share the maximum possible slack of the activity along that path according to its share. • Sum of the possible slacks of the activities can not exceed the maximum slack along that path. 21

Free slack of an activity • This is the maximum possible delay of an activity which does not affect its immediate successors. • This is evaluated as • FSij = ESj – EFij 22

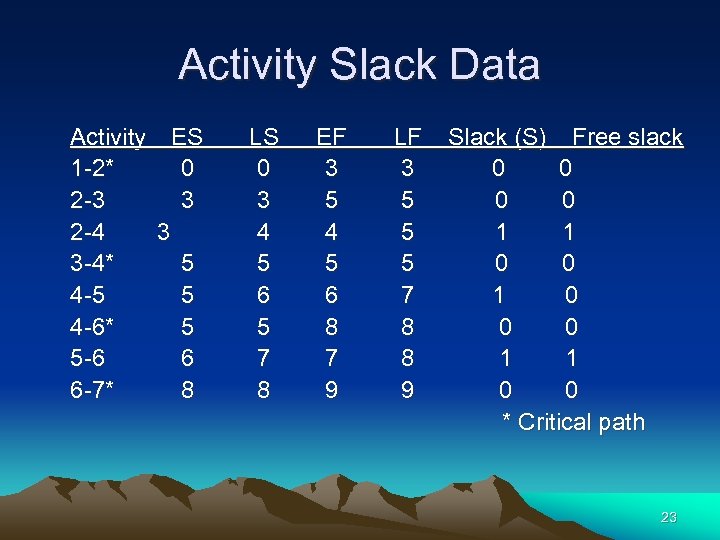
Activity Slack Data Activity ES 1 -2* 0 2 -3 3 2 -4 3 3 -4* 5 4 -5 5 4 -6* 5 5 -6 6 6 -7* 8 LS 0 3 4 5 6 5 7 8 EF 3 5 4 5 6 8 7 9 LF 3 5 5 5 7 8 8 9 Slack (S) Free slack 0 0 1 1 0 0 * Critical path 23

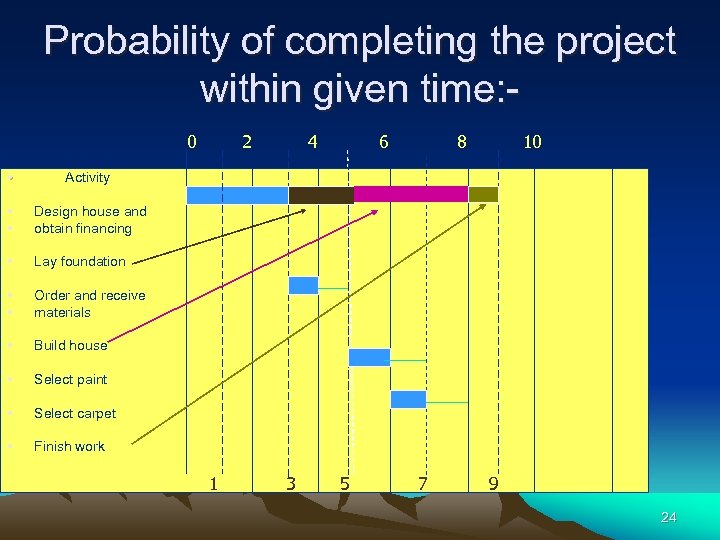
Probability of completing the project within given time: 0 • Build house • Select paint • Select carpet • 10 Order and receive materials • 8 Lay foundation • • 6 Design house and obtain financing • 4 Activity • • 2 Finish work 1 3 5 7 9 24

Probabilistic Time Estimates • Reflect uncertainty of activity times • Beta distribution is used in PERT a + 4 m + b Mean (expected time): t = 6 where, Variance: s 2 = ( b - a) 6 2 a = optimistic estimate m = most likely time estimate b = pessimistic time estimate 25

P (time) Example Beta Distributions a b t a t m b P (time) m a m=t b 26

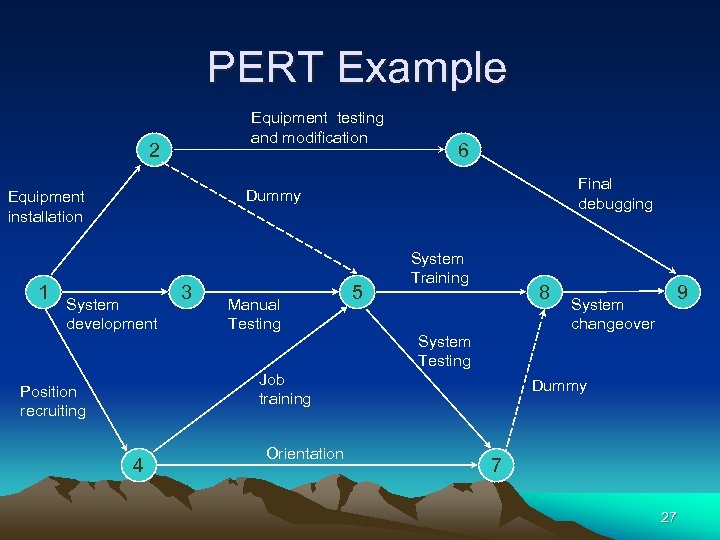
PERT Example Equipment testing and modification 2 Final debugging Dummy Equipment installation 1 6 System development 3 Manual Testing Job training Position recruiting 4 Orientation 5 System Training 8 System Testing System changeover 9 Dummy 7 27

Activity Information Activity 1 -2 1 -3 1 -4 2 -5 2 -6 3 -5 4 -7 5 -8 5 -7 7 -8 6 -9 8 -9 Time estimates (wks) a m b t 6 3 1 0 2 2 3 2 0 1 1 8 6 3 0 4 3 4 2 7 4 0 4 10 10 9 5 0 12 4 5 2 11 6 0 7 13 Mean Time s 2 8 6 3 0 5 3 4 2 7 4 0 4 9 Variance. 44 1. 00. 44. 00 2. 78. 11. 00 1. 78. 44. 00 1. 00 4. 00 28

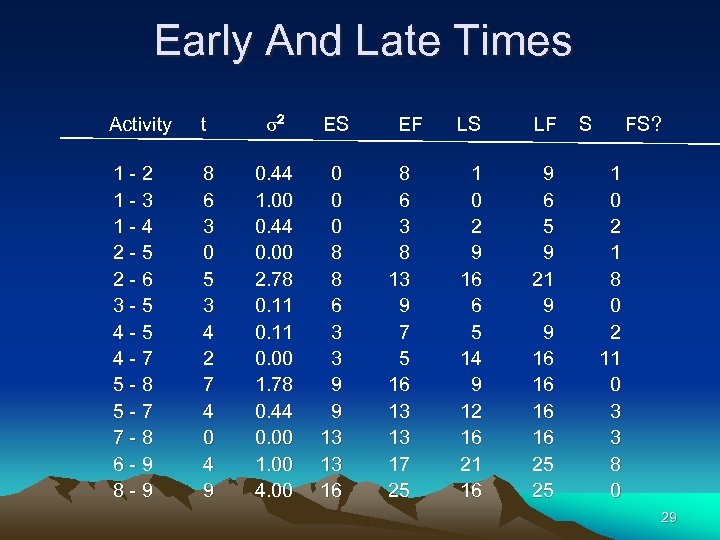
Early And Late Times Activity t s 2 ES 1 -2 1 -3 1 -4 2 -5 2 -6 3 -5 4 -7 5 -8 5 -7 7 -8 6 -9 8 6 3 0 5 3 4 2 7 4 0 4 9 0. 44 1. 00 0. 44 0. 00 2. 78 0. 11 0. 00 1. 78 0. 44 0. 00 1. 00 4. 00 0 8 8 6 3 3 9 9 13 13 16 EF 8 6 3 8 13 9 7 5 16 13 13 17 25 LS LF 1 0 2 9 16 6 5 14 9 12 16 21 16 9 6 5 9 21 9 9 16 16 25 25 S FS? 1 0 2 1 8 0 2 11 0 3 3 8 0 29

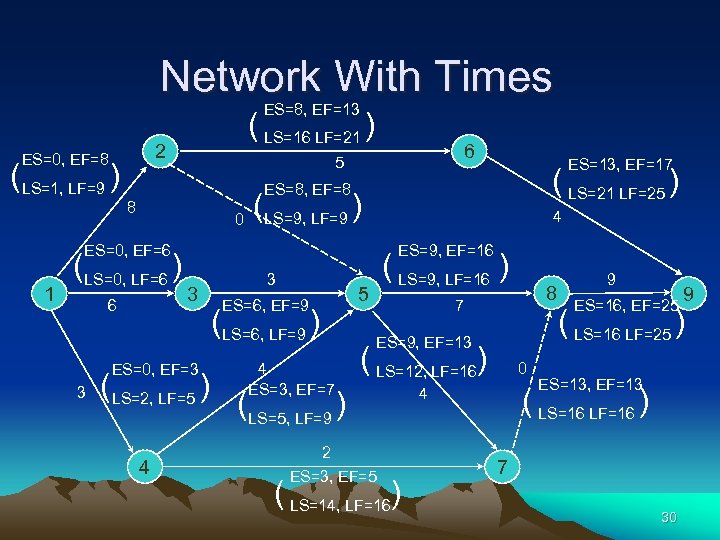
Network With Times ES=8, EF=13 2 ES=0, EF=8 (LS=1, LF=9 ) ( LS=16 LF=21 ) 6 5 8 0 (LS=0, LF=6 ) 6 (LS=9, LF=9 ) 4 ES=9, EF=16 3 ES=0, EF=3 3 ( LS=21 LF=25 ) ES=8, EF=8 ES=0, EF=6 1 ES=13, EF=17 (LS=2, LF=5 ) 4 3 ( LS=9, LF=16 ) 5 ES=6, EF=9 (LS=6, LF=9 ) 8 7 ES=9, EF=13 4 ES=3, EF=7 (LS=5, LF=9 ) ( LS=12, LF=16) 2 ES=3, EF=5 ( LS=14, LF=16) 0 9 ES=16, EF=25 ( LS=16 LF=25 ) ES=13, EF=13 ( LS=16 LF=16 ) 4 9 7 30

Project Variance Project variance is the sum of the variances along the critical path s 2 = s 2 13 + s 2 35 + s 2 58 + s 2 89 = 1. 00 +0. 11 + 1. 78 + 4. 00 = 6. 89 weeks 31

Probabilistic Network Analysis Determine the probability that a project is completed (project completion time is ) within a specified period of time x-m Z = where s m = tp = project mean time s = project standard deviation x = project time (random variable) Z = number of standard deviations of x from the mean (standardized random variable) 32

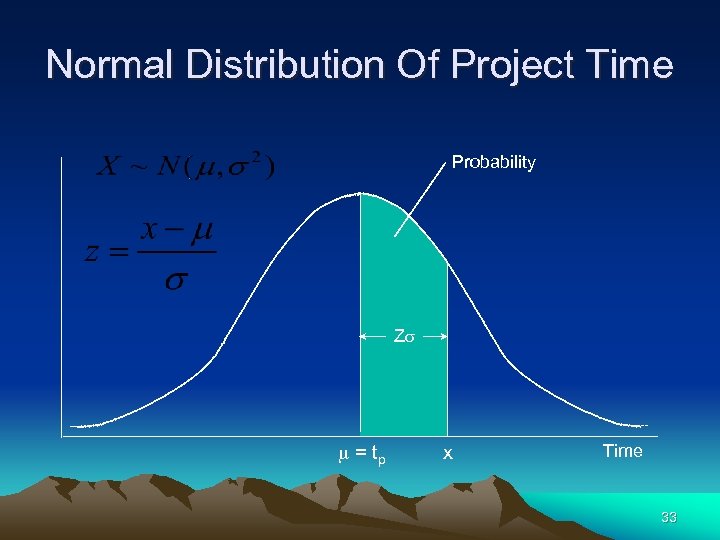
Normal Distribution Of Project Time Probability Zs m = tp x Time 33

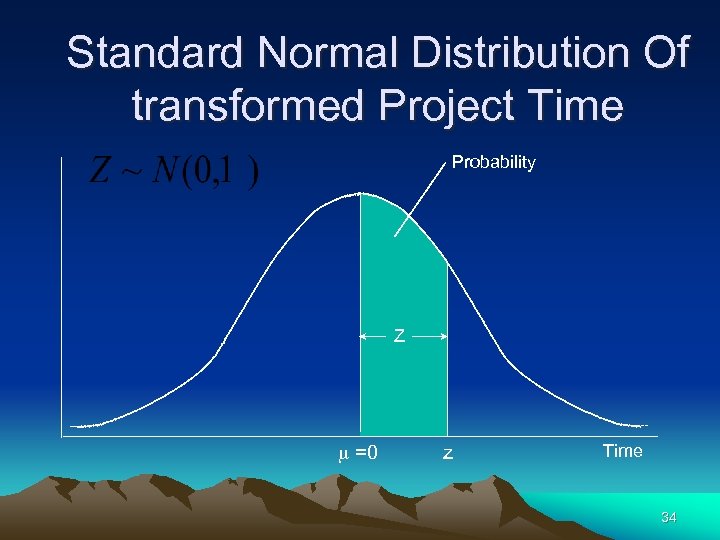
Standard Normal Distribution Of transformed Project Time Probability Z m =0 z Time 34

Probabilistic Analysis Example What is the probability that the project is completed within 30 weeks? P(X 30) = ? s 2 = 6. 89 weeks s = 6. 89 = 2. 62 weeks Z = x - m =30 - 25 = 1. 91 2. 62 s P(Z 1. 91) = ? 35

Determining Probability From Z Value Z 0. 00 . . 1. 1. . . 0. 3643. 1. 9 0. 4713 0. 01. . 04 . . 0. 3665 0. 3729. +0. 4719 … … 0. 09 0. 4767 P( x < 30 weeks) = 0. 50+ 04719 = 0. 9719 m = 25 x = 30 Time (weeks) 36

What is the probability that the project will be completed within 22 weeks? 22 - 25 = -3 = -1. 14 Z= 2. 62 P(Z< -1. 14) = 0. 1271 x = 22 m = 25 x=28 Time (weeks) P( x< 22 weeks) = 0. 1271 37

Benefits of PERT/CPM • Useful at many stages of project management • Mathematically simple • Uses graphical displays • Gives critical path & slack time • Provides project documentation • Useful in monitoring costs 38

Advantages of PERT/CPM Networks generated provide valuable project documentation and graphically point out who is responsible for various project activities Applicable to a wide variety of projects and industries Useful in monitoring not only schedules, but costs as well 39

Limitations of PERT/CPM • Assumes clearly defined, independent, & stable activities • Specified precedence relationships • Activity times (PERT) follow beta distribution • Subjective time estimates • Over-emphasis on critical path 40

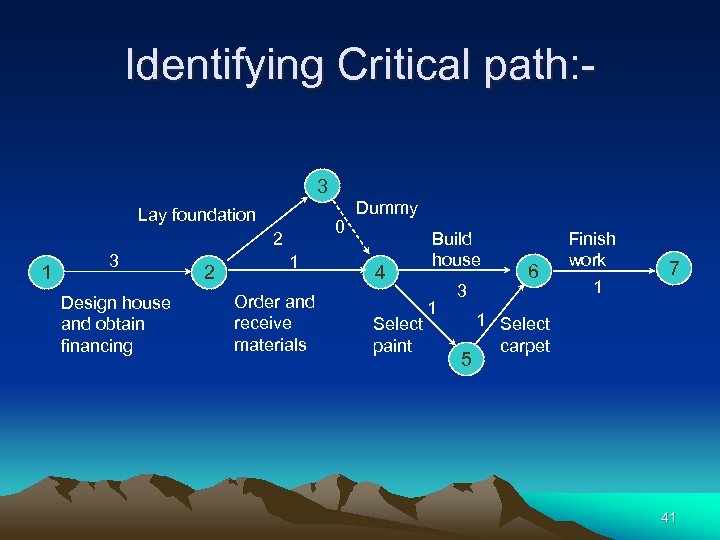
Identifying Critical path: 3 Lay foundation 1 3 Design house and obtain financing 2 2 0 1 Order and receive materials Dummy 4 Select paint Build house 1 3 5 6 Finish work 1 7 1 Select carpet 41

Project crashing: • When the two methods like work study, trade off and other possible ones fail, we go for crashing. • Crashing includes: Normal cost Normal Time Crash cost Crash Time Direct cost Indirect cost optimization cost