Unit 2 Exploring Data Comparisons and Relationships Topic

Unit 2 Exploring Data: Comparisons and Relationships Topic 9 Correlation Coefficient (page 185)

Lists you will need in your calculator for this topic: ACC 60 CMPG EXM 1 A EXM 1 B EXM 1 C EXM 2 A EXM 2 B EXM 2 C FCAP FWGT HMPG HOTEL HOUSE LFEXP MILE MONTH ORING PERTV PNUM POS PRICE PUBF PUBT RALEI RENT TEMP WGT … and the program CORR & SCATSIM

OVERVIEW You have seen how scatterplots provide useful visual information about the relationship between two quantitative variables. Just as you made use of numerical summaries of various aspects of the distribution of a single variable, it would also be handy to have a numerical measure of the association between two variables.

OVERVIEW This topic introduces you to just such a measure and asks you to investigate some of its properties. This measure is one of the most famous in statistics: the correlation coefficient.

Do the Preliminaries (page 186)

Essential Question What are the properties of the correlation coefficient as a numerical measure of the degree of association between two variables?

Activity 9 -1 Properties of Correlation (page 186) correlation coefficient r The _____________, denoted by ___, is a measure of the degree to which two variables are associated.

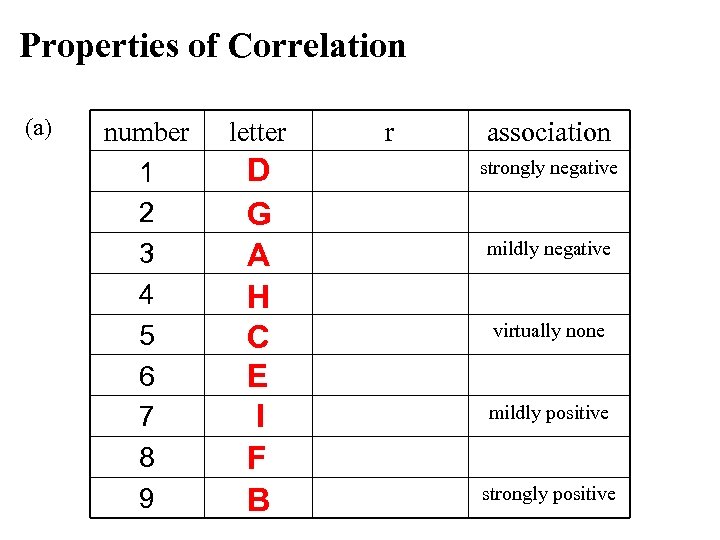Properties of Correlation (a) number 1 2 3 4 5 6 7 8 9 letter D G A H C E I F B r association strongly negative mildly negative virtually none mildly positive strongly positive

Please be sure you have the following lists: ACC 60 … time to accelerate from 0 to 60 mph CMPG … city miles per gallon rating FCAP … fuel capacity FWGT … % front weight HMPG … highway miles per gallon rating MILE … time to cover the quarter mile PNUM … page number on which the car appeared WGT … weight of the car … and the program CORR.

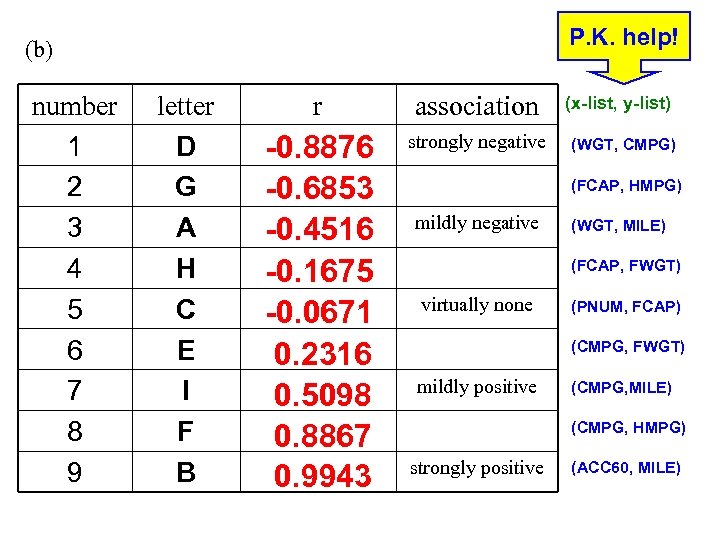P. K. help! (b) number 1 2 3 4 5 6 7 8 9 letter D G A H C E I F B r association -0. 8876 -0. 6853 -0. 4516 -0. 1675 -0. 0671 0. 2316 0. 5098 0. 8867 0. 9943 strongly negative (x-list, y-list) (WGT, CMPG) (FCAP, HMPG) mildly negative (WGT, MILE) (FCAP, FWGT) virtually none (PNUM, FCAP) (CMPG, FWGT) mildly positive (CMPG, MILE) (CMPG, HMPG) strongly positive (ACC 60, MILE)

(c) I would believe that the largest value the correlation coefficient can assume is 1 -1 ___ and that the smallest value the correlation coefficient can assume is ____. (d) I believe that in order for the correlation coefficient to assume its largest or smallest value, the data would have to fall … … exactly on a straight line. association (e) The sign of the correlation matches the direction of the _________. (+ or -) (f) The stronger the association, the closer the correlation comes to ______. ± 1 0 The weaker the association, the closer the correlation comes to ______.

+1 The correlation coefficient has to be between ___ and -1 __. If it is equal to one of these values, then the observations line form a straight ______. The sign of the correlation reflects the direction of the _____ association. The magnitude of the correlation indicates the strength _____ +1 -1 of the association, with values closer to ____ or ____ signifying stronger associations.

(g) Does there seem to be any relationship between temperature and month in Raleigh? _______ YES curvilinear The data reveal a _____________ relationship. (h) [Copy lists named MONTH and RALEI. ] 0. 2571 correlation coefficient = ______ yes/no? Are you surprised? _______ weak positive Its value seems to indicate a ______________ relationship. [explain] This is not consistent with the answer to part (g). And that is because r measures strength of a linear association. Line is the root of linear!

linear The correlation coefficient measures only ______ (straight-line) relationships between two variables. undetected Curvilinear relationships can go ________ by r. scatterplot Therefore, always examine a ________ as well as the value of r. Therefore, always examine a ________ as well as scatterplot the value of r.

(i) [Copy lists named PUBT and PUBF. ] 0. 5065 correlation coefficient = ______ yes/no? Are you surprised? _______ moderate positive Its value seems to indicate a _______________ relationship. [explain] The correlation coefficient is a higher value than what the scatterplot appears to show.

Essential Question Is the correlation coefficient resistant?

Activity 9 -2 Monopoly Prices (pages 165 to 167) As of 1999, the wheeling and dealing board game Monopoly is the most played board game. It has been played by an estimated 500 million people worldwide. (a) [Copy lists named PRICE and RENT. ] My guess as to the value of the correlation coefficient your guess between rent and price is … ______.

(b) 0. 9711 correlation coefficient = ______ [explain] (c) Are you surprised? yes/no? _______ The points almost lie in a straight line. Boardwalk price 400 400 100 1 1 Boardwalk rent 50 100 1 1000 50 50 100 guess for correlation actual correlation your guess . 9711 Make a scatterplot first, guess the correlation, then calculate the correlation.

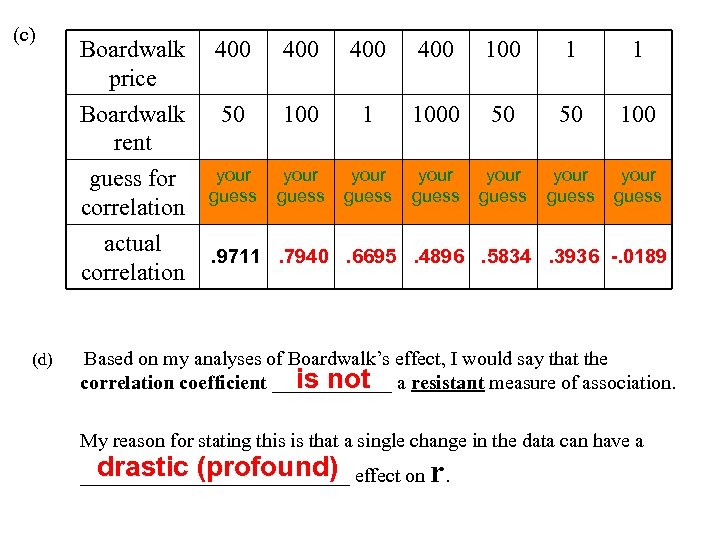(c) 400 400 100 1 1 Boardwalk rent 50 100 1 1000 50 50 100 guess for correlation your guess your guess actual correlation (d) Boardwalk price . 9711. 7940. 6695. 4896. 5834. 3936 -. 0189 Based on my analyses of Boardwalk’s effect, I would say that the is not correlation coefficient ______ a resistant measure of association. My reason for stating this is that a single change in the data can have a drastic (profound) ______________ effect on. r

The formula for the calculation for the correlation coefficient (r) is: r = ith where : xi denotes the ______ observation of one variable, ith yi denotes the ______ observation of the other variable, ______ and ______ the respective sample means, s sx y ______ and ______ the respective sample standard deviations , and n the sample size.

Essential Question What are the properties of the correlation coefficient as a numerical measure of the degree of association between two variables?

Activity 9 -3 Cars Fuel Efficiency (continued) (pages 168 & 169) Remember how to calculate a z-score? xi = value of interest x = mean sx = standard deviation

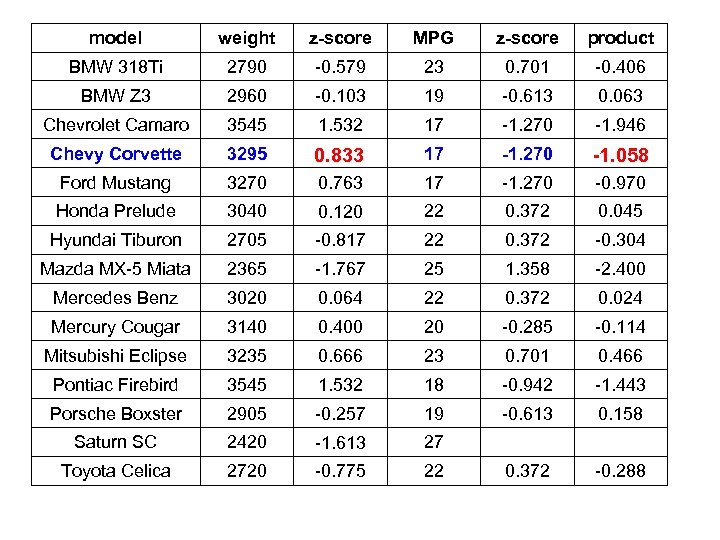
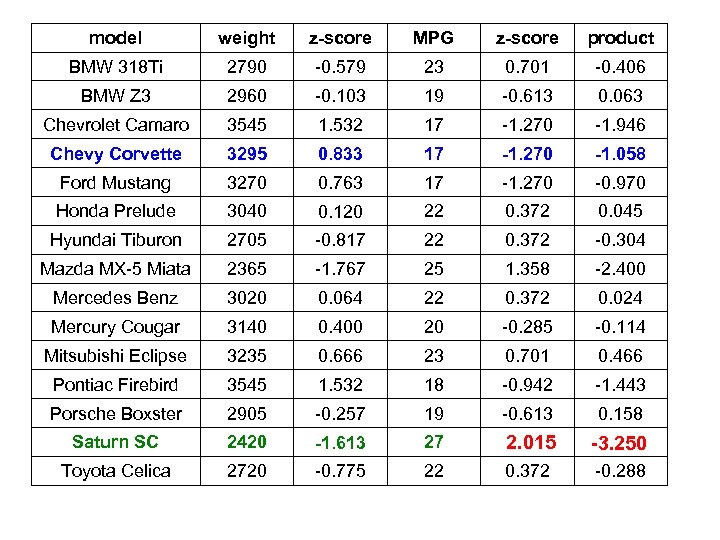
(a) Calculation for the z-score for the weight of a Chevy Corvette: mean for the weights = x = 2997 pounds standard deviation for the weights = sx = 357. 6 pounds Corvette weight = xi = 3295 pounds = 0. 833 Z-score. Corvette weight x Z-score. Corvette MPG = ( 0. 833)(-1. 270) = -1. 058

model weight z-score MPG z-score product BMW 318 Ti 2790 -0. 579 23 0. 701 -0. 406 BMW Z 3 2960 -0. 103 19 -0. 613 0. 063 Chevrolet Camaro 3545 1. 532 17 -1. 270 -1. 946 Chevy Corvette 3295 0. 833 17 -1. 270 -1. 058 Ford Mustang 3270 0. 763 17 -1. 270 -0. 970 Honda Prelude 3040 0. 120 22 0. 372 0. 045 Hyundai Tiburon 2705 -0. 817 22 0. 372 -0. 304 Mazda MX-5 Miata 2365 -1. 767 25 1. 358 -2. 400 Mercedes Benz 3020 0. 064 22 0. 372 0. 024 Mercury Cougar 3140 0. 400 20 -0. 285 -0. 114 Mitsubishi Eclipse 3235 0. 666 23 0. 701 0. 466 Pontiac Firebird 3545 1. 532 18 -0. 942 -1. 443 Porsche Boxster 2905 -0. 257 19 -0. 613 0. 158 Saturn SC 2420 -1. 613 27 Toyota Celica 2720 -0. 775 22 0. 372 -0. 288

Calculation for the z-score for the MPG rating of a Saturn SC: mean for the MPG ratings = y = 20. 867 mpg standard deviation for the MPG ratings = sy = 3. 044 mpg Saturn SC mpg rating = yi = 27 mpg = 2. 015 Z-score. Saturn weight x Z-score. Saturn MPG = ( -1. 613)(2. 015) = -3. 250

model weight z-score MPG z-score product BMW 318 Ti 2790 -0. 579 23 0. 701 -0. 406 BMW Z 3 2960 -0. 103 19 -0. 613 0. 063 Chevrolet Camaro 3545 1. 532 17 -1. 270 -1. 946 Chevy Corvette 3295 0. 833 17 -1. 270 -1. 058 Ford Mustang 3270 0. 763 17 -1. 270 -0. 970 Honda Prelude 3040 0. 120 22 0. 372 0. 045 Hyundai Tiburon 2705 -0. 817 22 0. 372 -0. 304 Mazda MX-5 Miata 2365 -1. 767 25 1. 358 -2. 400 Mercedes Benz 3020 0. 064 22 0. 372 0. 024 Mercury Cougar 3140 0. 400 20 -0. 285 -0. 114 Mitsubishi Eclipse 3235 0. 666 23 0. 701 0. 466 Pontiac Firebird 3545 1. 532 18 -0. 942 -1. 443 Porsche Boxster 2905 -0. 257 19 -0. 613 0. 158 Saturn SC 2420 -1. 613 27 2. 015 -3. 250 Toyota Celica 2720 -0. 775 22 0. 372 -0. 288

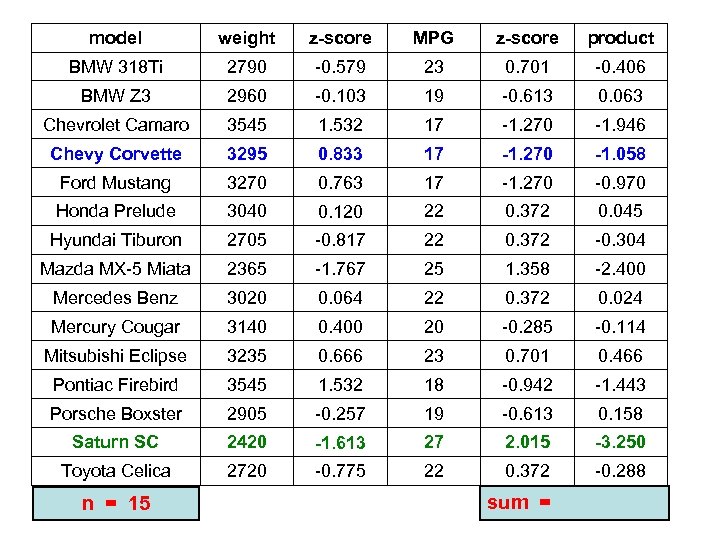model weight z-score MPG z-score product BMW 318 Ti 2790 -0. 579 23 0. 701 -0. 406 BMW Z 3 2960 -0. 103 19 -0. 613 0. 063 Chevrolet Camaro 3545 1. 532 17 -1. 270 -1. 946 Chevy Corvette 3295 0. 833 17 -1. 270 -1. 058 Ford Mustang 3270 0. 763 17 -1. 270 -0. 970 Honda Prelude 3040 0. 120 22 0. 372 0. 045 Hyundai Tiburon 2705 -0. 817 22 0. 372 -0. 304 Mazda MX-5 Miata 2365 -1. 767 25 1. 358 -2. 400 Mercedes Benz 3020 0. 064 22 0. 372 0. 024 Mercury Cougar 3140 0. 400 20 -0. 285 -0. 114 Mitsubishi Eclipse 3235 0. 666 23 0. 701 0. 466 Pontiac Firebird 3545 1. 532 18 -0. 942 -1. 443 Porsche Boxster 2905 -0. 257 19 -0. 613 0. 158 Saturn SC 2420 -1. 613 27 2. 015 -3. 250 Toyota Celica 2720 -0. 775 22 0. 372 -0. 288 n = 15 sum =

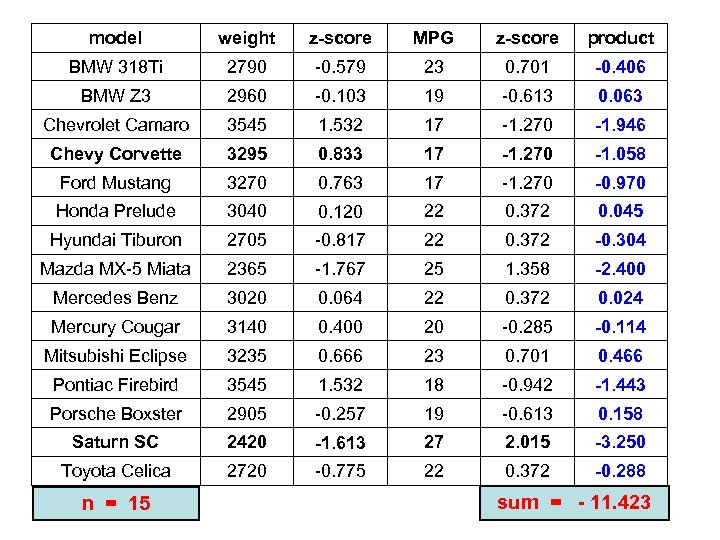model weight z-score MPG z-score product BMW 318 Ti 2790 -0. 579 23 0. 701 -0. 406 BMW Z 3 2960 -0. 103 19 -0. 613 0. 063 Chevrolet Camaro 3545 1. 532 17 -1. 270 -1. 946 Chevy Corvette 3295 0. 833 17 -1. 270 -1. 058 Ford Mustang 3270 0. 763 17 -1. 270 -0. 970 Honda Prelude 3040 0. 120 22 0. 372 0. 045 Hyundai Tiburon 2705 -0. 817 22 0. 372 -0. 304 Mazda MX-5 Miata 2365 -1. 767 25 1. 358 -2. 400 Mercedes Benz 3020 0. 064 22 0. 372 0. 024 Mercury Cougar 3140 0. 400 20 -0. 285 -0. 114 Mitsubishi Eclipse 3235 0. 666 23 0. 701 0. 466 Pontiac Firebird 3545 1. 532 18 -0. 942 -1. 443 Porsche Boxster 2905 -0. 257 19 -0. 613 0. 158 Saturn SC 2420 -1. 613 27 2. 015 -3. 250 Toyota Celica 2720 -0. 775 22 0. 372 -0. 288 n = 15 sum = - 11. 423

The formula for the calculation for the correlation coefficient (r) is: r = ith where : xi denotes the ______ observation of one variable, ith yi denotes the ______ observation of the other variable, ______ and ______ the respective sample means, s sx y ______ and ______ the respective sample standard deviations , and n the sample size.

- 0. 8159 (b) The correlation coefficient between weight & MPG is _____. n = 15, so … = - 0. 8159

(c) The MPG z-score of most of the cars with negative weight z-scores tend to be positive values ___________. [explain] The positive z-score values of one variable will correspond to negative z-score values of the other variable. Remember the association for weight and MPG was negative. positive value x negative value = negative value

Assignment Activity 9 -6: Properties of Correlation (continued) (page 197) Assignment Activity 9 -7: Properties of Correlation (continued) (page 197) Assignment Activity 9 -8: Properties of Correlation (continued) (page 198)

Essential Question What is the distinction between correlation and causation?

Activity 9 -4 Televisions and Life Expectancy (pages 193 & 194) U. S. 1. 3 (a) Country with the fewest people per television set is _______, with ____. Haiti 234 Country with the most people per television set is ____, with ____. (b) [Copy lists named LFEXP and PERTV. ] Make a scatterplot of Life expectancy vs. people per TV X-list is PERTV and Y-list is LFEXP

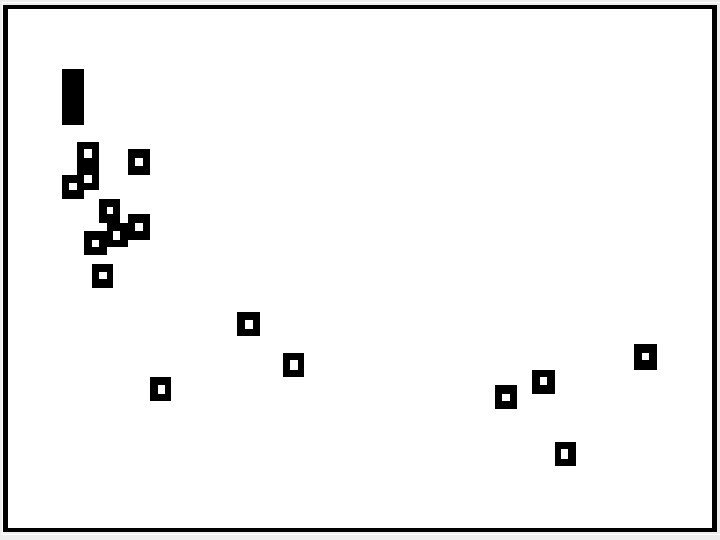
(b) [Copy lists named LFEXP and PERTV. ] YES Does there appear to be an association between the two variables? ______ strong negative The association seems to indicate a ______________ relationship, longer since the countries with less people per TV have a ________ life expectancy.

(c) The correlation coefficient between life expectancy and people -0. 8038 per TV is ______. (d) [comment] How absurd it would be to send TV’s to countries with lower life expectancies to cause their inhabitants to live longer. These variables are obviously associated with another variable. (e) If two variables have a correlation close to +1 or to -1, indicating a strong linear association between them, must there be a cause-and-effect relationship between them? NO _______

Two variables may be strongly associated (as measured by the correlation coefficient) cause effect without a _____ -and- ____ relationship existing between them. both Often the explanation is that _______ variables third are related to a _______ variable not being measured … which is called lurking confounding a _____ or ________ variable.

(f) In the case of life expectancy and television sets, a confounding variable associated with a country’s life expectancy and with the prevalence of televisions in the country would be … The wealth of the country The location of the country Correlation does not mean causation!

Assignment Activity 9 -12: Monopoly Prices (continued) (page 200) Assignment Activity 9 -15: Ice Cream, Drownings, and Fire Damage (page 202) Assignment Activity 9 -18: Space Shuttle O-Ring Failures (continued) (page 204)

Essential Question Can you judge a correlation value from a scatterplot?

Activity 9 -5 Guess the Correlation (page 195) This activity will give you practice at judging the value of a correlation coefficient by examining the scatterplot. Have fun with this activity!

(a) [Copy the program SCATSIM. ] Before running this program, delete all lists that are not needed. Please follow the directions when you run the program. Be sure to make a guess before pressing the ENTER key. Be careful to include the (-) key for negative correlations. Record your guesses and actual values in the chart.

(b) Write your guess for your SCORE before pressing ENTER! (c) Record your SCORE and comment whether you are surprised. REPEAT (a) through (c) See if you can beat your previous SCORE. REPEAT (a) through (c) again! See if you can beat the highest class SCORE.

Be careful to include the (-) key for negative correlations. Note: This program makes lists called GUESS and ACTUA. If you miss an entry, record it on your paper, continue with the program, place GUESS and ACTUA in the Set. Up. Editor, then correct the entry. Run the program CORR to get your correct SCORE (correlation coefficient). Record your guesses and actual values in the chart.

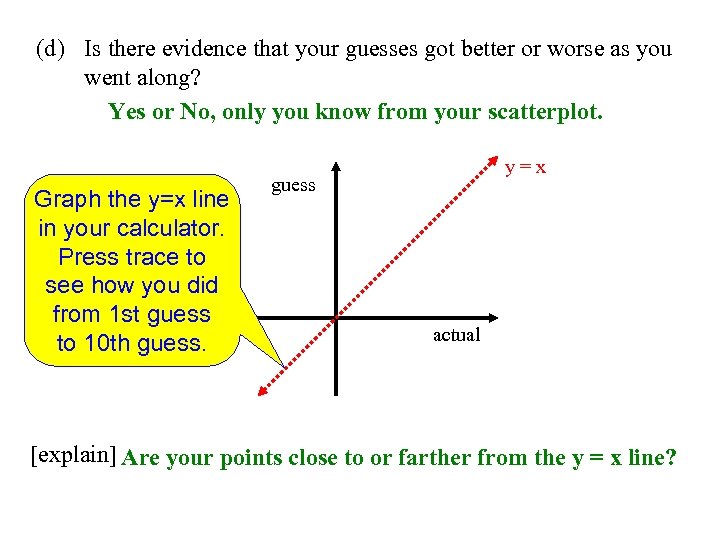(d) Is there evidence that your guesses got better or worse as you went along? Yes or No, only you know from your scatterplot. Graph the y=x line in your calculator. Press trace to see how you did from 1 st guess to 10 th guess. y=x guess actual [explain] Are your points close to or farther from the y = x line?

(e) Is there evidence that you are better at guessing certain values of correlation than others? Yes or No, only you know from your scatterplot. ERROR = GUESS - ACTUAL ERROR is automatically made by the program SCATSIM. error = 0 (no error) actual If you were a great guesser, then all of your points should be on or very close to the actual (x) axis.

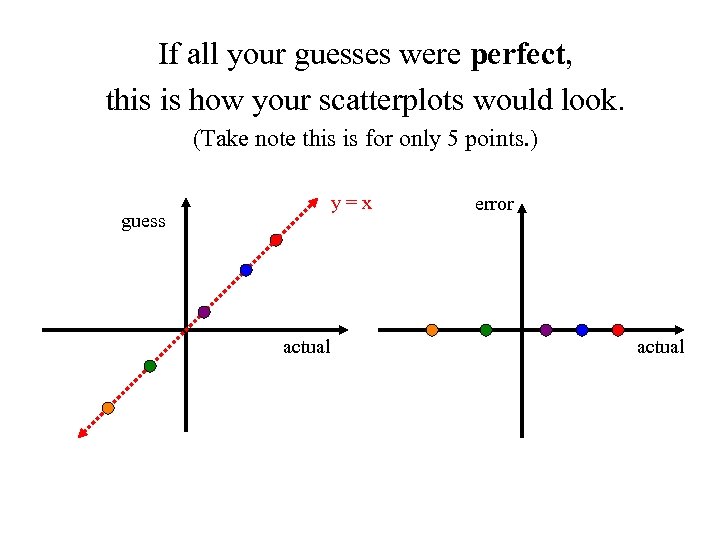If all your guesses were perfect, this is how your scatterplots would look. (Take note this is for only 5 points. ) y=x guess actual error actual

(f) If all of my guesses were too high by exactly 0. 1, then the correlation between my guesses and the actual values would 1. 0 be _______. (g) If all of my guesses were too high by exactly 0. 5, then the correlation between my guesses and the actual values would be _______. 1. 0 y=x guess actual error actual

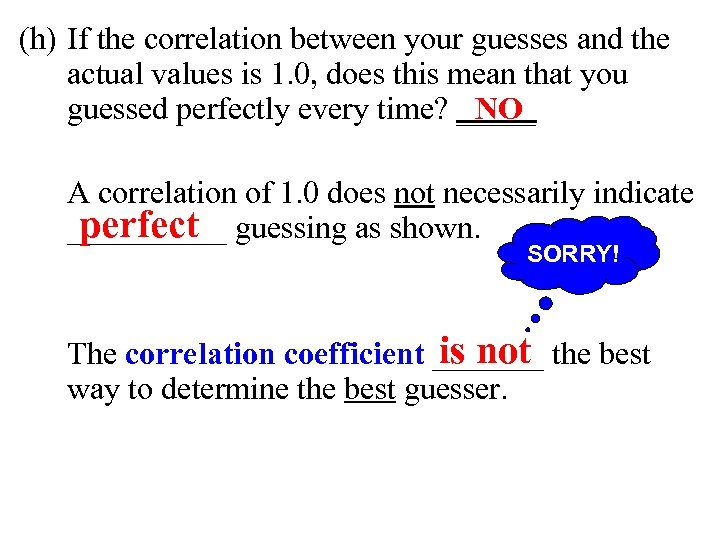(h) If the correlation between your guesses and the actual values is 1. 0, does this mean that you NO guessed perfectly every time? _____ A correlation of 1. 0 does not necessarily indicate perfect _____ guessing as shown. SORRY! is not The correlation coefficient _______ the best way to determine the best guesser.

WRAP-UP In this topic you have discovered the very important correlation coefficient as a measure of the linear relationship between two variables. You have derived some of the properties of this measure, such as the values it can assume, how its sign and value relate to the direction and strength of the association, and its lack of resistance to outliers.

WRAP-UP You have also practiced judging the direction and strength of a relationship from looking at a scatterplot. In addition, you have discovered the distinction between correlation and causation and learned that one needs to be very careful about inferring causal relationships between variables based solely on a strong correlation.

WRAP-UP The next topic will expand your understanding of relationships between variables by introducing you to least squares regression, a formal mathematical model that is often useful for describing such relationships.

Your topic is due! Quiz on Topic 9: Correlation Coefficient