d01bd09eb9cb24822f42b2a88cd6ecf9.ppt
- Количество слайдов: 105
 UNIT-1 MATHEMATICAL LOGIC
UNIT-1 MATHEMATICAL LOGIC
 Introduction: Logic? • We will study – Propositional Logic (PL) – First-Order Logic (FOL) • Logic – is the study of the logic relationships between objects and – forms the basis of all mathematical reasoning and all automated reasoning
Introduction: Logic? • We will study – Propositional Logic (PL) – First-Order Logic (FOL) • Logic – is the study of the logic relationships between objects and – forms the basis of all mathematical reasoning and all automated reasoning
 Introduction: PL? • Propositional Logic (PL) = Propositional Calculus = Sentential Logic • In Propositional Logic, the objects are called propositions • Definition: A proposition is a statement that is either true or false, but not both • We usually denote a proposition by a letter: p, q, r, s, …
Introduction: PL? • Propositional Logic (PL) = Propositional Calculus = Sentential Logic • In Propositional Logic, the objects are called propositions • Definition: A proposition is a statement that is either true or false, but not both • We usually denote a proposition by a letter: p, q, r, s, …
 Outline • Defining Propositional Logic – – Propositions Connectives Precedence of Logical Operators Truth tables • Usefulness of Logic – Bitwise operations – Logic in Theoretical Computer Science (SAT) – Logic in Programming • Logical Equivalences – Terminology – Truth tables – Equivalence rules
Outline • Defining Propositional Logic – – Propositions Connectives Precedence of Logical Operators Truth tables • Usefulness of Logic – Bitwise operations – Logic in Theoretical Computer Science (SAT) – Logic in Programming • Logical Equivalences – Terminology – Truth tables – Equivalence rules
 Introduction: Proposition • Definition: The value of a proposition is called its truth value; denoted by – T or 1 if it is true or – F or 0 if it is false • Opinions, interrogative, and imperative are not propositions • Truth table p 0 1
Introduction: Proposition • Definition: The value of a proposition is called its truth value; denoted by – T or 1 if it is true or – F or 0 if it is false • Opinions, interrogative, and imperative are not propositions • Truth table p 0 1
 Propositions: Examples • The following are propositions – Today is Monday – The grass is wet – It is raining M W R • The following are not propositions – C++ is the best language – When is the pretest? – Do your homework Opinion Interrogative Imperative
Propositions: Examples • The following are propositions – Today is Monday – The grass is wet – It is raining M W R • The following are not propositions – C++ is the best language – When is the pretest? – Do your homework Opinion Interrogative Imperative
 Are these propositions? • 2+2=5 • Every integer is divisible by 12 • Microsoft is an excellent company
Are these propositions? • 2+2=5 • Every integer is divisible by 12 • Microsoft is an excellent company
 Logical connectives • Connectives are used to create a compound proposition from two or more propositions Negation (e. g. , a or !a or ā) $neg$, $bar$ And or logical conjunction (denoted ) $wedge$ OR or logical disjunction (denoted ) $vee$ XOR or exclusive or (denoted ) $oplus$ Impli ion (denoted or ) $Rightarrow$, $rightarrow$ – Biconditional (denoted or ) $Left. Rightarrow$, $leftrightarrow$ – – – • We define the meaning (semantics) of the logical connectives using truth tables
Logical connectives • Connectives are used to create a compound proposition from two or more propositions Negation (e. g. , a or !a or ā) $neg$, $bar$ And or logical conjunction (denoted ) $wedge$ OR or logical disjunction (denoted ) $vee$ XOR or exclusive or (denoted ) $oplus$ Impli ion (denoted or ) $Rightarrow$, $rightarrow$ – Biconditional (denoted or ) $Left. Rightarrow$, $leftrightarrow$ – – – • We define the meaning (semantics) of the logical connectives using truth tables
 Precedence of Logical Operators • As in arithmetic, an ordering is imposed on the use of logical operators in compound propositions • However, it is preferable to use parentheses to disambiguate operators and facilitate readability p q r ( p) (q ( r)) • To avoid unnecessary parenthesis, the following precedences hold: 1. 2. 3. 4. 5. Negation ( ) Conjunction ( ) Disjunction ( ) Implication ( ) Biconditional ( )
Precedence of Logical Operators • As in arithmetic, an ordering is imposed on the use of logical operators in compound propositions • However, it is preferable to use parentheses to disambiguate operators and facilitate readability p q r ( p) (q ( r)) • To avoid unnecessary parenthesis, the following precedences hold: 1. 2. 3. 4. 5. Negation ( ) Conjunction ( ) Disjunction ( ) Implication ( ) Biconditional ( )
 Logical Connective: Negation • p, the negation of a proposition p, is also a proposition • Examples: – Today is not Monday – It is not the case that today is Monday, etc. • Truth table p p 0 1 1 0
Logical Connective: Negation • p, the negation of a proposition p, is also a proposition • Examples: – Today is not Monday – It is not the case that today is Monday, etc. • Truth table p p 0 1 1 0
 Logical Connective: Logical And • The logical connective And is true only when both of the propositions are true. It is also called a conjunction • Examples – It is raining and it is warm – (2+3=5) and (1<2) – Schroedinger’s cat is dead and Schroedinger’s cat is not dead. • Truth table p q 0 0 0 1 1 p q
Logical Connective: Logical And • The logical connective And is true only when both of the propositions are true. It is also called a conjunction • Examples – It is raining and it is warm – (2+3=5) and (1<2) – Schroedinger’s cat is dead and Schroedinger’s cat is not dead. • Truth table p q 0 0 0 1 1 p q
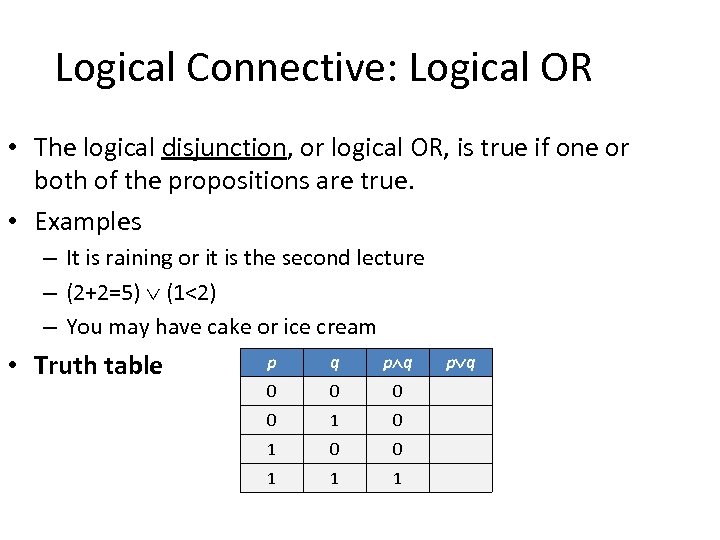 Logical Connective: Logical OR • The logical disjunction, or logical OR, is true if one or both of the propositions are true. • Examples – It is raining or it is the second lecture – (2+2=5) (1<2) – You may have cake or ice cream • Truth table p q 0 0 1 1 1 p q
Logical Connective: Logical OR • The logical disjunction, or logical OR, is true if one or both of the propositions are true. • Examples – It is raining or it is the second lecture – (2+2=5) (1<2) – You may have cake or ice cream • Truth table p q 0 0 1 1 1 p q
 Logical Connective: Exclusive Or • The exclusive OR, or XOR, of two propositions is true when exactly one of the propositions is true and the other one is false • Example – The circuit is either ON or OFF but not both – Let ab<0, then either a<0 or b<0 but not both – You may have cake or ice cream, but not both • Truth table p q p q 0 0 0 1 1 1 p q
Logical Connective: Exclusive Or • The exclusive OR, or XOR, of two propositions is true when exactly one of the propositions is true and the other one is false • Example – The circuit is either ON or OFF but not both – Let ab<0, then either a<0 or b<0 but not both – You may have cake or ice cream, but not both • Truth table p q p q 0 0 0 1 1 1 p q
 Logical Connective: Implication (1) • Definition: Let p and q be two propositions. The implication p q is the proposition that is false when p is true and q is false and true otherwise – p is called the hypothesis, antecedent, premise – q is called the conclusion, consequence • Truth table p q p q 0 0 0 1 0 1 1 1 0 p q
Logical Connective: Implication (1) • Definition: Let p and q be two propositions. The implication p q is the proposition that is false when p is true and q is false and true otherwise – p is called the hypothesis, antecedent, premise – q is called the conclusion, consequence • Truth table p q p q 0 0 0 1 0 1 1 1 0 p q
 Logical Connective: Implication (2) • The implication of p q can be also read as – If p then q – p implies q – If p, q – p only if q – q if p – q whenever p – q follows from p – p is a sufficient condition for q (p is sufficient for q) – q is a necessary condition for p (q is necessary for p)
Logical Connective: Implication (2) • The implication of p q can be also read as – If p then q – p implies q – If p, q – p only if q – q if p – q whenever p – q follows from p – p is a sufficient condition for q (p is sufficient for q) – q is a necessary condition for p (q is necessary for p)
 Logical Connective: Implication (3) • Examples – If you buy you air ticket in advance, it is cheaper. – If x is an integer, then x 2 0. – If it rains, the grass gets wet. – If the sprinklers operate, the grass gets wet. – If 2+2=5, then all unicorns are pink.
Logical Connective: Implication (3) • Examples – If you buy you air ticket in advance, it is cheaper. – If x is an integer, then x 2 0. – If it rains, the grass gets wet. – If the sprinklers operate, the grass gets wet. – If 2+2=5, then all unicorns are pink.
 Exercise: Which of the following implications is true? • If -1 is a positive number, then 2+2=5 True. The premise is obviously false, thus no matter what the conclusion is, the implication holds. • If -1 is a positive number, then 2+2=4 True. Same as above. • If sin x = 0, then x = 0 False. x can be a multiple of . If we let x=2 , then sin x=0 but x 0. The implication “if sin x = 0, then x = k , for some k” is true.
Exercise: Which of the following implications is true? • If -1 is a positive number, then 2+2=5 True. The premise is obviously false, thus no matter what the conclusion is, the implication holds. • If -1 is a positive number, then 2+2=4 True. Same as above. • If sin x = 0, then x = 0 False. x can be a multiple of . If we let x=2 , then sin x=0 but x 0. The implication “if sin x = 0, then x = k , for some k” is true.
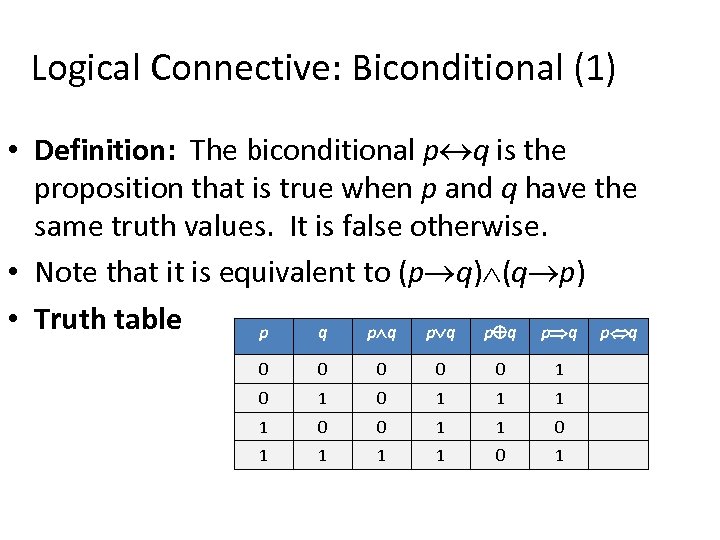 Logical Connective: Biconditional (1) • Definition: The biconditional p q is the proposition that is true when p and q have the same truth values. It is false otherwise. • Note that it is equivalent to (p q) (q p) • Truth table p q p q p q 0 0 0 1 0 1 1 0 0 1 1 1 1 0 1
Logical Connective: Biconditional (1) • Definition: The biconditional p q is the proposition that is true when p and q have the same truth values. It is false otherwise. • Note that it is equivalent to (p q) (q p) • Truth table p q p q p q 0 0 0 1 0 1 1 0 0 1 1 1 1 0 1
 Logical Connective: Biconditional (2) • The biconditional p q can be equivalently read as – p if and only if q – p is a necessary and sufficient condition for q – if p then q, and conversely – p iff q (Note typo in textbook, page 9, line 3) • Examples – x>0 if and only if x 2 is positive – The alarm goes off iff a burglar breaks in – You may have pudding iff you eat your meat
Logical Connective: Biconditional (2) • The biconditional p q can be equivalently read as – p if and only if q – p is a necessary and sufficient condition for q – if p then q, and conversely – p iff q (Note typo in textbook, page 9, line 3) • Examples – x>0 if and only if x 2 is positive – The alarm goes off iff a burglar breaks in – You may have pudding iff you eat your meat
 Exercise: Which of the following biconditionals is true? • x 2 + y 2 = 0 if and only if x=0 and y=0 True. Both implications hold • 2 + 2 = 4 if and only if 2<2 True. Both implications hold. • x 2 0 if and only if x 0 False. The implication “if x 0 then x 2 0” holds. However, the implication “if x 2 0 then x 0” is false. Consider x=-1. The hypothesis (-1)2=1 0 but the conclusion fails.
Exercise: Which of the following biconditionals is true? • x 2 + y 2 = 0 if and only if x=0 and y=0 True. Both implications hold • 2 + 2 = 4 if and only if 2<2 True. Both implications hold. • x 2 0 if and only if x 0 False. The implication “if x 0 then x 2 0” holds. However, the implication “if x 2 0 then x 0” is false. Consider x=-1. The hypothesis (-1)2=1 0 but the conclusion fails.
 Converse, Inverse, Contrapositive • Consider the proposition p q – Its converse is the proposition q p – Its inverse is the proposition p q – Its contrapositive is the proposition q p
Converse, Inverse, Contrapositive • Consider the proposition p q – Its converse is the proposition q p – Its inverse is the proposition p q – Its contrapositive is the proposition q p
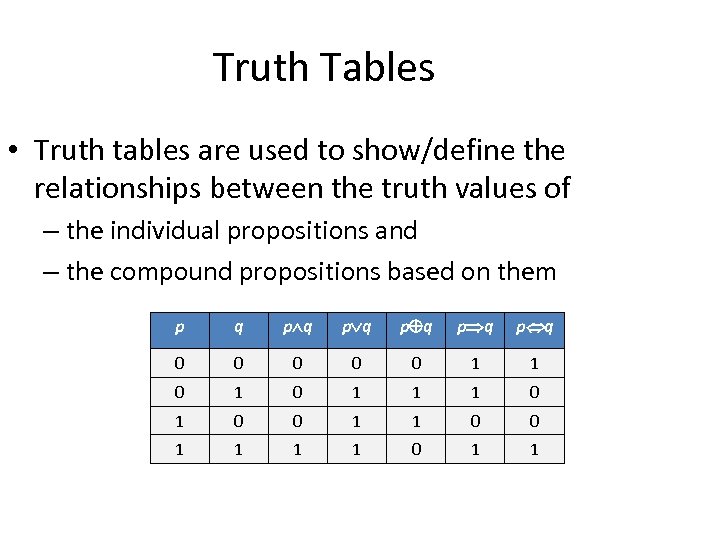 Truth Tables • Truth tables are used to show/define the relationships between the truth values of – the individual propositions and – the compound propositions based on them p q p q p q 0 0 0 1 1 1 0 0 1 1 0 1 1
Truth Tables • Truth tables are used to show/define the relationships between the truth values of – the individual propositions and – the compound propositions based on them p q p q p q 0 0 0 1 1 1 0 0 1 1 0 1 1
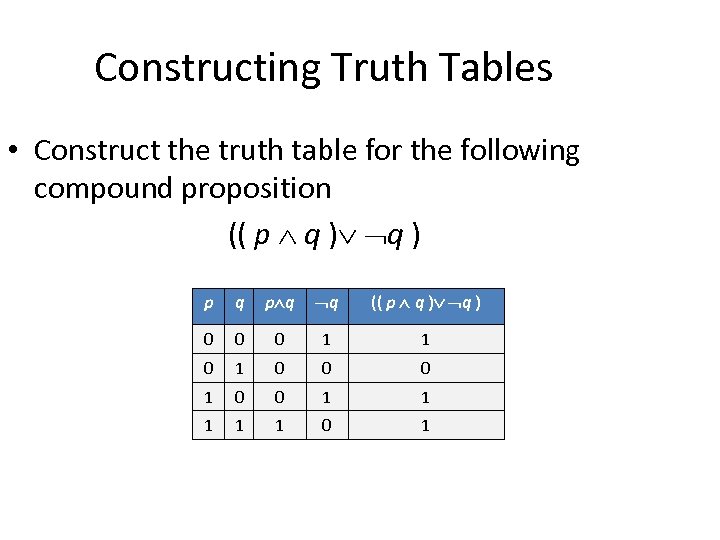 Constructing Truth Tables • Construct the truth table for the following compound proposition (( p q ) p q q (( p q ) 0 0 0 1 1 1 0 1
Constructing Truth Tables • Construct the truth table for the following compound proposition (( p q ) p q q (( p q ) 0 0 0 1 1 1 0 1
 Outline • Defining Propositional Logic – – Propositions Connectives Precedence of Logical Operators Truth tables • Usefulness of Logic – Bitwise operations – Logic in Theoretical Computer Science (SAT) – Logic in Programming • Logical Equivalences – Terminology – Truth tables – Equivalence rules
Outline • Defining Propositional Logic – – Propositions Connectives Precedence of Logical Operators Truth tables • Usefulness of Logic – Bitwise operations – Logic in Theoretical Computer Science (SAT) – Logic in Programming • Logical Equivalences – Terminology – Truth tables – Equivalence rules
 Usefulness of Logic • Logic is more precise than natural language – You may have cake or ice cream. • Can I have both? – If you buy your air ticket in advance, it is cheaper. • Are there or not cheap last-minute tickets? • For this reason, logic is used for hardware and software specification – Given a set of logic statements, – One can decide whether or not they are satisfiable (i. e. , consistent), although this is a costly process…
Usefulness of Logic • Logic is more precise than natural language – You may have cake or ice cream. • Can I have both? – If you buy your air ticket in advance, it is cheaper. • Are there or not cheap last-minute tickets? • For this reason, logic is used for hardware and software specification – Given a set of logic statements, – One can decide whether or not they are satisfiable (i. e. , consistent), although this is a costly process…
 Bitwise Operations Computers represent information as bits (binary digits) A bit string is a sequence of bits The length of the string is the number of bits in the string Logical connectives can be applied to bit strings of equal length • Example 0110 1010 1101 0010 1111 _______ Bitwise OR 0111 1010 1111 Bitwise AND. . . Bitwise XOR … • •
Bitwise Operations Computers represent information as bits (binary digits) A bit string is a sequence of bits The length of the string is the number of bits in the string Logical connectives can be applied to bit strings of equal length • Example 0110 1010 1101 0010 1111 _______ Bitwise OR 0111 1010 1111 Bitwise AND. . . Bitwise XOR … • •
 Logic in TCS • What is SAT? SAT is the problem of determining whether or not a sentence in propositional logic (PL) is satisfiable. – Given: a PL sentence – Question: Determine whether or not it is satisfiable • Characterizing SAT as an NP-complete problem (complexity class) is at the foundation of Theoretical Computer Science. • What is a PL sentence? What does satisfiable mean?
Logic in TCS • What is SAT? SAT is the problem of determining whether or not a sentence in propositional logic (PL) is satisfiable. – Given: a PL sentence – Question: Determine whether or not it is satisfiable • Characterizing SAT as an NP-complete problem (complexity class) is at the foundation of Theoretical Computer Science. • What is a PL sentence? What does satisfiable mean?
 Logic in TCS: A Sentence in PL • A Boolean variable is a variable that can have a value 1 or 0. Thus, Boolean variable is a proposition. • A term is a Boolean variable • A literal is a term or its negation • A clause is a disjunction of literals • A sentence in PL is a conjunction of clauses • Example: (a b c d) ( b c) ( a c d) • A sentence in PL is satisfiable iff – we can assign a truth value – to each Boolean variables – such that the sentence evaluates to true (i. e. , holds)
Logic in TCS: A Sentence in PL • A Boolean variable is a variable that can have a value 1 or 0. Thus, Boolean variable is a proposition. • A term is a Boolean variable • A literal is a term or its negation • A clause is a disjunction of literals • A sentence in PL is a conjunction of clauses • Example: (a b c d) ( b c) ( a c d) • A sentence in PL is satisfiable iff – we can assign a truth value – to each Boolean variables – such that the sentence evaluates to true (i. e. , holds)
 SAT in TCS • Problem – Given: A sentence in PL (a complex proposition), which is • Boolean variables connected with logical connectives • Usually, as a conjunction of clauses (CNF = Conjunctive Normal Form) – Question: • Find an assignment of truth values (0/1) • That makes the sentence true, i. e. the sentence holds
SAT in TCS • Problem – Given: A sentence in PL (a complex proposition), which is • Boolean variables connected with logical connectives • Usually, as a conjunction of clauses (CNF = Conjunctive Normal Form) – Question: • Find an assignment of truth values (0/1) • That makes the sentence true, i. e. the sentence holds
 Logic in Programming: Example 1 • Say you need to define a conditional statement as follows: – Increment x if the following condition holds (x > 0 and x < 10) or x=10 • You may try: If (0
Logic in Programming: Example 1 • Say you need to define a conditional statement as follows: – Increment x if the following condition holds (x > 0 and x < 10) or x=10 • You may try: If (0
 Logic in Programming: Example 2 • Say we have the following loop While ((i
Logic in Programming: Example 2 • Say we have the following loop While ((i
 Outline • Defining Propositional Logic – – Propositions Connectives Precedence of Logical Operators Truth tables • Usefulness of Logic – Bitwise operations – Logic in Theoretical Computer Science (SAT) – Logic in Programming • Logical Equivalences – Terminology – Truth tables – Equivalence rules
Outline • Defining Propositional Logic – – Propositions Connectives Precedence of Logical Operators Truth tables • Usefulness of Logic – Bitwise operations – Logic in Theoretical Computer Science (SAT) – Logic in Programming • Logical Equivalences – Terminology – Truth tables – Equivalence rules
 Propositional Equivalences: Introduction • To manipulate a set of statements (here, logical propositions) for the sake of mathematical argumentation, an important step is to replace one statement with another equivalent statement (i. e. , with the same truth value) • Below, we discuss – Terminology – Establishing logical equivalences using truth tables – Establishing logical equivalences using known laws (of logical equivalences)
Propositional Equivalences: Introduction • To manipulate a set of statements (here, logical propositions) for the sake of mathematical argumentation, an important step is to replace one statement with another equivalent statement (i. e. , with the same truth value) • Below, we discuss – Terminology – Establishing logical equivalences using truth tables – Establishing logical equivalences using known laws (of logical equivalences)
 Terminology: Tautology, Contradictions, Contingencies • Definitions – A compound proposition that is always true, no matter what the truth values of the propositions that occur in it is called a tautology – A compound proposition that is always false is called a contradiction – A proposition that is neither a tautology nor a contradiction is a contingency • Examples – A simple tautology is p p – A simple contradiction is p p
Terminology: Tautology, Contradictions, Contingencies • Definitions – A compound proposition that is always true, no matter what the truth values of the propositions that occur in it is called a tautology – A compound proposition that is always false is called a contradiction – A proposition that is neither a tautology nor a contradiction is a contingency • Examples – A simple tautology is p p – A simple contradiction is p p
 Logical Equivalences: Definition • Definition: Propositions p and q are logically equivalent if p q is a tautology. • Informally, p and q are equivalent if whenever p is true, q is true, and vice versa • Notation: p q (p is equivalent to q), p q, and p q • Alert: is not a logical connective $equiv$
Logical Equivalences: Definition • Definition: Propositions p and q are logically equivalent if p q is a tautology. • Informally, p and q are equivalent if whenever p is true, q is true, and vice versa • Notation: p q (p is equivalent to q), p q, and p q • Alert: is not a logical connective $equiv$
 Logical Equivalences: Example 1 • Are the propositions (p q) and ( p q) logically equivalent? • To find out, we construct the truth tables for each: p q p p q 0 0 0 1 1 The two columns in the truth table are identical, thus we conclude that (p q) ( p q)
Logical Equivalences: Example 1 • Are the propositions (p q) and ( p q) logically equivalent? • To find out, we construct the truth tables for each: p q p p q 0 0 0 1 1 The two columns in the truth table are identical, thus we conclude that (p q) ( p q)
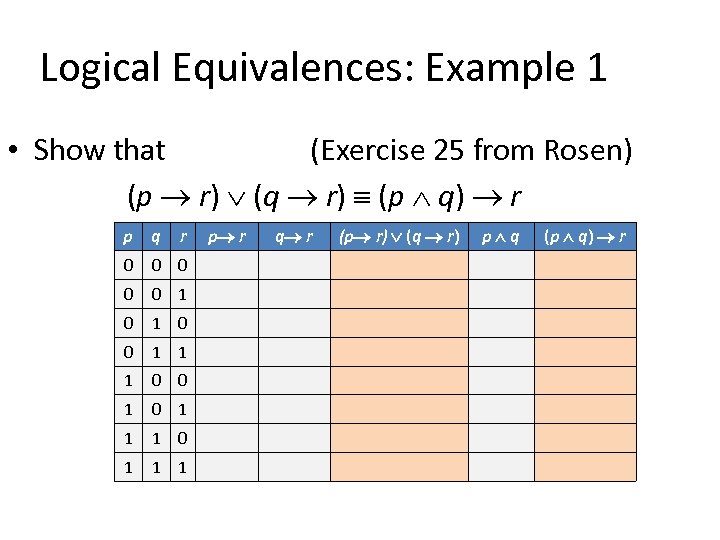 Logical Equivalences: Example 1 • Show that (Exercise 25 from Rosen) (p r) (q r) (p q) r p q r 0 0 0 1 1 1 0 0 1 1 1 p r q r (p r) (q r) p q (p q) r
Logical Equivalences: Example 1 • Show that (Exercise 25 from Rosen) (p r) (q r) (p q) r p q r 0 0 0 1 1 1 0 0 1 1 1 p r q r (p r) (q r) p q (p q) r
 Propositional Equivalences: Introduction • To manipulate a set of statements (here, logical propositions) for the sake of mathematical argumentation, an important step is to replace one statement with another equivalent statement (i. e. , with the same truth value) • Below, we discuss – Terminology – Establishing logical equivalences using truth tables – Establishing logical equivalences using known laws (of logical equivalences)
Propositional Equivalences: Introduction • To manipulate a set of statements (here, logical propositions) for the sake of mathematical argumentation, an important step is to replace one statement with another equivalent statement (i. e. , with the same truth value) • Below, we discuss – Terminology – Establishing logical equivalences using truth tables – Establishing logical equivalences using known laws (of logical equivalences)
 Logical Equivalences: Cheat Sheet • Table of logical equivalences can be found in Rosen (page 24) • These and other can be found in a handout on the course web page: http: //www. cse. unl. edu/~cse 235/files/Logical. Equivalences. pdf • Let’s take a quick look at this Cheat Sheet
Logical Equivalences: Cheat Sheet • Table of logical equivalences can be found in Rosen (page 24) • These and other can be found in a handout on the course web page: http: //www. cse. unl. edu/~cse 235/files/Logical. Equivalences. pdf • Let’s take a quick look at this Cheat Sheet
 Using Logical Equivalences: Example 1 • Logical equivalences can be used to construct additional logical equivalences • Example: Show that (p q) q is a tautology 0. (p q) q 1. (p q) q 2. ( p q) q 3. p ( q q) 4. p 1 5. 1 Implication Law on 0 De Morgan’s Law (1 st) on 1 Associative Law on 2 Negation Law on 3 Domination Law on 4
Using Logical Equivalences: Example 1 • Logical equivalences can be used to construct additional logical equivalences • Example: Show that (p q) q is a tautology 0. (p q) q 1. (p q) q 2. ( p q) q 3. p ( q q) 4. p 1 5. 1 Implication Law on 0 De Morgan’s Law (1 st) on 1 Associative Law on 2 Negation Law on 3 Domination Law on 4
 My Advice • • Remove double implication Replace implication by disjunction Push negation inwards Distribute
My Advice • • Remove double implication Replace implication by disjunction Push negation inwards Distribute
 Using Logical Equivalences: Example 2 • Example (Exercise 17)*: Show that (p q) • Sometimes it helps to start with the second proposition (p q) 0. (p q) 1. (p q) ( q p) Equivalence Law on 0 2. ( p q) (q p) Implication Law on 1 3. ( (( p q) (q p))) Double negation on 2 4. ( ( p q) (q p)) De Morgan’s Law… 5. ((p q) ( q p)) De Morgan’s Law 6. ((p q) (p p) (q q) (q p)) Distribution Law 7. ((p q) (q p)) Identity Law 8. ((q p ) (p q)) Implication Law 9. (p q) Equivalence Law *See Table 8 (p 25) but you are not allowed to use the table for the proof
Using Logical Equivalences: Example 2 • Example (Exercise 17)*: Show that (p q) • Sometimes it helps to start with the second proposition (p q) 0. (p q) 1. (p q) ( q p) Equivalence Law on 0 2. ( p q) (q p) Implication Law on 1 3. ( (( p q) (q p))) Double negation on 2 4. ( ( p q) (q p)) De Morgan’s Law… 5. ((p q) ( q p)) De Morgan’s Law 6. ((p q) (p p) (q q) (q p)) Distribution Law 7. ((p q) (q p)) Identity Law 8. ((q p ) (p q)) Implication Law 9. (p q) Equivalence Law *See Table 8 (p 25) but you are not allowed to use the table for the proof
 Using Logical Equivalences: Example 3 • Show that (q p) (p q) q 0. (q p) (p q) 1. ( q p) (p q) Implication Law 2. (q p) (p q) De Morgan’s & Double negation 3. (q p) 4. q ( p p) 5. q 1 q Commutative Law Distributive Law Identity Law
Using Logical Equivalences: Example 3 • Show that (q p) (p q) q 0. (q p) (p q) 1. ( q p) (p q) Implication Law 2. (q p) (p q) De Morgan’s & Double negation 3. (q p) 4. q ( p p) 5. q 1 q Commutative Law Distributive Law Identity Law
 Proving Logical Equivalences: Summary • Proving two PL sentences A, B are equivalent using TT + EL 1. Verify that the 2 columns of A, B in the truth table are the same (i. e. , A, B have the same models) 2. Verify that the column of (A B B A) in the truth table has all-1 entries (it is a tautology) 3. Put A, B in CNF, they should be the same • Sequence of equivalence laws: Biconditional, implication, moving negation inwards, distributivity 4. Apply a sequence of inference laws • • • Starting from one sentence, usually the most complex one, Until reaching the second sentence Typical sequence: Biconditional, implication, moving negation inwards, distributivity
Proving Logical Equivalences: Summary • Proving two PL sentences A, B are equivalent using TT + EL 1. Verify that the 2 columns of A, B in the truth table are the same (i. e. , A, B have the same models) 2. Verify that the column of (A B B A) in the truth table has all-1 entries (it is a tautology) 3. Put A, B in CNF, they should be the same • Sequence of equivalence laws: Biconditional, implication, moving negation inwards, distributivity 4. Apply a sequence of inference laws • • • Starting from one sentence, usually the most complex one, Until reaching the second sentence Typical sequence: Biconditional, implication, moving negation inwards, distributivity
![Logic in Programming: Example 2 (revisited) • Recall the loop While ((i<size AND A[i]>10) Logic in Programming: Example 2 (revisited) • Recall the loop While ((i<size AND A[i]>10)](https://present5.com/presentation/d01bd09eb9cb24822f42b2a88cd6ecf9/image-45.jpg) Logic in Programming: Example 2 (revisited) • Recall the loop While ((i
Logic in Programming: Example 2 (revisited) • Recall the loop While ((i
 Programming Pitfall Note • In C, C++ and Java, applying the commutative law is not such a good idea. • For example, consider accessing an integer array A of size n: if (i
Programming Pitfall Note • In C, C++ and Java, applying the commutative law is not such a good idea. • For example, consider accessing an integer array A of size n: if (i
 Predicate Logic and Quantifies
Predicate Logic and Quantifies
 Outline • Introduction • Terminology: – Propositional functions; arguments; arity; universe of discourse • Quantifiers – Definition; using, mixing, negating them • Logic Programming (Prolog) • Transcribing English to Logic • More exercises
Outline • Introduction • Terminology: – Propositional functions; arguments; arity; universe of discourse • Quantifiers – Definition; using, mixing, negating them • Logic Programming (Prolog) • Transcribing English to Logic • More exercises
 Introduction • Consider the statements: x>3, x=y+3, x+y=z • The symbols >, +, = denote relations between x and 3, x, y, and 4, and x, y, and z, respectively • These relations may hold or not hold depending on the values that x, y, and z may take. • A predicate is a property that is affirmed or denied about the subject (in logic, we say ‘variable’ or ‘argument’) of a statement • Consider the statement : ‘x is greater than 3’ – ‘x’ is the subject – ‘is greater than 3’ is the predicate
Introduction • Consider the statements: x>3, x=y+3, x+y=z • The symbols >, +, = denote relations between x and 3, x, y, and 4, and x, y, and z, respectively • These relations may hold or not hold depending on the values that x, y, and z may take. • A predicate is a property that is affirmed or denied about the subject (in logic, we say ‘variable’ or ‘argument’) of a statement • Consider the statement : ‘x is greater than 3’ – ‘x’ is the subject – ‘is greater than 3’ is the predicate
 Propositional Functions (1) • To write in Predicate Logic ‘x is greater than 3’ – We introduce a functional symbol for the predicate and – Put the subject as an argument (to the functional symbol): P(x) • Terminology – P(x) is a statement – P is a predicate or propositional function – x as an argument
Propositional Functions (1) • To write in Predicate Logic ‘x is greater than 3’ – We introduce a functional symbol for the predicate and – Put the subject as an argument (to the functional symbol): P(x) • Terminology – P(x) is a statement – P is a predicate or propositional function – x as an argument
 Propositional Functions (2) • Examples: – – Father(x): unary predicate Brother(x. y): binary predicate Sum(x, y, z): ternary predicate P(x, y, z, t): n-ary predicate
Propositional Functions (2) • Examples: – – Father(x): unary predicate Brother(x. y): binary predicate Sum(x, y, z): ternary predicate P(x, y, z, t): n-ary predicate
 Propositional Functions (3) • Definition: A statement of the form P(x 1, x 2, …, xn) is the value of the propositional symbol P. • Here: (x 1, x 2, …, xn) is an n-tuple and P is a predicate • We can think of a propositional function as a function that – – Evaluates to true or false Takes one or more arguments Expresses a predicate involving the argument(s) Becomes a proposition when values are assigned to the arguments
Propositional Functions (3) • Definition: A statement of the form P(x 1, x 2, …, xn) is the value of the propositional symbol P. • Here: (x 1, x 2, …, xn) is an n-tuple and P is a predicate • We can think of a propositional function as a function that – – Evaluates to true or false Takes one or more arguments Expresses a predicate involving the argument(s) Becomes a proposition when values are assigned to the arguments
 Propositional Functions: Example • Let Q(x, y, z) denote the statement ‘x 2+y 2=z 2’ – What is the truth value of Q(3, 4, 5)? Q(3, 4, 5) is true – What is the truth value of Q(2, 2, 3)? Q(2, 3, 3) is false – How many values of (x, y, z) make the predicate true? There are infinitely many values that make the proposition true, how many right triangles are there?
Propositional Functions: Example • Let Q(x, y, z) denote the statement ‘x 2+y 2=z 2’ – What is the truth value of Q(3, 4, 5)? Q(3, 4, 5) is true – What is the truth value of Q(2, 2, 3)? Q(2, 3, 3) is false – How many values of (x, y, z) make the predicate true? There are infinitely many values that make the proposition true, how many right triangles are there?
 Universe of Discourse • Consider the statement ‘x>3’, does it make sense to assign to x the value ‘blue’? • Intuitively, the universe of discourse is the set of all things we wish to talk about; that is the set of all objects that we can sensibly assign to a variable in a propositional function. • What would be the universe of discourse for the propositional function below be: Enrolled. CSE 235(x)=‘x is enrolled in CSE 235’
Universe of Discourse • Consider the statement ‘x>3’, does it make sense to assign to x the value ‘blue’? • Intuitively, the universe of discourse is the set of all things we wish to talk about; that is the set of all objects that we can sensibly assign to a variable in a propositional function. • What would be the universe of discourse for the propositional function below be: Enrolled. CSE 235(x)=‘x is enrolled in CSE 235’
 Universe of Discourse: Multivariate functions • Each variable in an n-tuple (i. e. , each argument) may have a different universe of discourse • Consider an n-ary predicate P: P(r, g, b, c)= ‘The rgb-values of the color c is (r, g, b)’ • Example, what is the truth value of – P(255, 0, 0, red) – P(0, 0, 255, green) • What are the universes of discourse of (r, g, b, c)?
Universe of Discourse: Multivariate functions • Each variable in an n-tuple (i. e. , each argument) may have a different universe of discourse • Consider an n-ary predicate P: P(r, g, b, c)= ‘The rgb-values of the color c is (r, g, b)’ • Example, what is the truth value of – P(255, 0, 0, red) – P(0, 0, 255, green) • What are the universes of discourse of (r, g, b, c)?
 Outline • Introduction • Terminology: – Propositional functions; arguments; arity; universe of discourse • Quantifiers – Definition; using, mixing, negating them • Logic Programming (Prolog) • Transcribing English to Logic • More exercises
Outline • Introduction • Terminology: – Propositional functions; arguments; arity; universe of discourse • Quantifiers – Definition; using, mixing, negating them • Logic Programming (Prolog) • Transcribing English to Logic • More exercises
 Quantifiers: Introduction • The statement ‘x>3’ is not a proposition • It becomes a proposition – When we assign values to the argument: ‘ 4>3’ is false, ‘ 2<3’ is true, or – When we quantify the statement • Two quantifiers – Universal quantifier $forall$ the proposition is true for all possible values in the universe of discourse – Existential quantifier $exists$ the proposition is true for some value(s) in the universe of discourse
Quantifiers: Introduction • The statement ‘x>3’ is not a proposition • It becomes a proposition – When we assign values to the argument: ‘ 4>3’ is false, ‘ 2<3’ is true, or – When we quantify the statement • Two quantifiers – Universal quantifier $forall$ the proposition is true for all possible values in the universe of discourse – Existential quantifier $exists$ the proposition is true for some value(s) in the universe of discourse
 Universal Quantifier: Definition • Definition: The universal quantification of a predicate P(x) is the proposition ‘P(x) is true for all values of x in the universe of discourse. ’ We use the notation: x P(x), which is read ‘for all x’. • If the universe of discourse is finite, say {n 1, n 2, …, nk}, then the universal quantifier is simply the conjunction of the propositions over all the elements x P(x) P(n 1) P(n 2) … P(nk)
Universal Quantifier: Definition • Definition: The universal quantification of a predicate P(x) is the proposition ‘P(x) is true for all values of x in the universe of discourse. ’ We use the notation: x P(x), which is read ‘for all x’. • If the universe of discourse is finite, say {n 1, n 2, …, nk}, then the universal quantifier is simply the conjunction of the propositions over all the elements x P(x) P(n 1) P(n 2) … P(nk)
 Universal Quantifier: Example 1 • Let P(x): ‘x must take a discrete mathematics course’ and Q(x): ‘x is a CS student. ’ • The universe of discourse for both P(x) and Q(x) is all UNL students. • Express the statements: – “Every CS student must take a discrete mathematics course. ” x Q(x) P(x) – “Everybody must take a discrete mathematics course or be a CS student. ” x ( P(x) Q(x) ) – “Everybody must take a discrete mathematics course and be a CS student. ” x ( P(x) Q(x) ) Are these statements true or false?
Universal Quantifier: Example 1 • Let P(x): ‘x must take a discrete mathematics course’ and Q(x): ‘x is a CS student. ’ • The universe of discourse for both P(x) and Q(x) is all UNL students. • Express the statements: – “Every CS student must take a discrete mathematics course. ” x Q(x) P(x) – “Everybody must take a discrete mathematics course or be a CS student. ” x ( P(x) Q(x) ) – “Everybody must take a discrete mathematics course and be a CS student. ” x ( P(x) Q(x) ) Are these statements true or false?
 Universal Quantifier: Example 2 • Express the statement: ‘for every x and every y, x+y>10’ • Answer: – Let P(x, y) be the statement x+y>10 – Where the universe of discourse for x, y is the set of integers – The statement is: x y P(x, y) • Shorthand: x, y P(x, y)
Universal Quantifier: Example 2 • Express the statement: ‘for every x and every y, x+y>10’ • Answer: – Let P(x, y) be the statement x+y>10 – Where the universe of discourse for x, y is the set of integers – The statement is: x y P(x, y) • Shorthand: x, y P(x, y)
 Existential Quantifier: Definition • Definition: The existential quantification of a predicate P(x) is the proposition ‘There exists a value x in the universe of discourse such that P(x) is true. ’ We use the notation: x P(x), which is read ‘there exists x’. • If the universe of discourse is finite, say {n 1, n 2, …, nk}, then the existential quantifier is simply the disjunction of the propositions over all the elements x P(x) P(n 1) P(n 2) … P(nk)
Existential Quantifier: Definition • Definition: The existential quantification of a predicate P(x) is the proposition ‘There exists a value x in the universe of discourse such that P(x) is true. ’ We use the notation: x P(x), which is read ‘there exists x’. • If the universe of discourse is finite, say {n 1, n 2, …, nk}, then the existential quantifier is simply the disjunction of the propositions over all the elements x P(x) P(n 1) P(n 2) … P(nk)
 Existential Quantifier: Example 1 • Let P(x, y) denote the statement ‘x+y=5’ • What does the expression x y P(x, y) mean? • Which universe(s) of discourse make it true?
Existential Quantifier: Example 1 • Let P(x, y) denote the statement ‘x+y=5’ • What does the expression x y P(x, y) mean? • Which universe(s) of discourse make it true?
 Existential Quantifier: Example 2 • Express the statement: ‘there exists a real solution to ax 2+bxc=0’ • Answer: – Let P(x) be the statement x= (-b (b 2 -4 ac))/2 a – Where the universe of discourse for x is the set of real numbers. Note here that a, b, c are fixed constants. – The statement can be expressed as x P(x) • What is the truth value of x P(x)? – It is false. When b 2<4 ac, there are no real number x that can satisfy the predicate • What can we do so that x P(x)is true? – Change the universe of discourse to the complex numbers, C
Existential Quantifier: Example 2 • Express the statement: ‘there exists a real solution to ax 2+bxc=0’ • Answer: – Let P(x) be the statement x= (-b (b 2 -4 ac))/2 a – Where the universe of discourse for x is the set of real numbers. Note here that a, b, c are fixed constants. – The statement can be expressed as x P(x) • What is the truth value of x P(x)? – It is false. When b 2<4 ac, there are no real number x that can satisfy the predicate • What can we do so that x P(x)is true? – Change the universe of discourse to the complex numbers, C
 Quantifiers: Truth values • In general, when are quantified statements true or false? Statement True when… x P(x) False when. . . There is an x for which P(x) is true for every x P(x) is false There is an x for which P(x) is false for every x P(x) is true
Quantifiers: Truth values • In general, when are quantified statements true or false? Statement True when… x P(x) False when. . . There is an x for which P(x) is true for every x P(x) is false There is an x for which P(x) is false for every x P(x) is true
 Mixing quantifiers (1) • Existential and universal quantifiers can be used together to quantify a propositional predicate. For example: x y P(x, y) is perfectly valid • Alert: – The quantifiers must be read from left to right – The order of the quantifiers is important – x y P(x, y) is not equivalent to y x P(x, y)
Mixing quantifiers (1) • Existential and universal quantifiers can be used together to quantify a propositional predicate. For example: x y P(x, y) is perfectly valid • Alert: – The quantifiers must be read from left to right – The order of the quantifiers is important – x y P(x, y) is not equivalent to y x P(x, y)
 Mixing quantifiers (2) • Consider – x y Loves (x, y): Everybody loves somebody – y x Loves(x, y): There is someone loved by everyone • The two expressions do not mean the same thing • ( y x Loves(x, y)) ( x y Loves (x, y)) but the converse does not hold • However, you can commute similar quantifiers – x y P(x, y) is equivalent to y x P(x, y) (thus, x, y P(x, y)) – x y P(x, y) is equivalent to y x P(x, y) (thus x, y P(x, y))
Mixing quantifiers (2) • Consider – x y Loves (x, y): Everybody loves somebody – y x Loves(x, y): There is someone loved by everyone • The two expressions do not mean the same thing • ( y x Loves(x, y)) ( x y Loves (x, y)) but the converse does not hold • However, you can commute similar quantifiers – x y P(x, y) is equivalent to y x P(x, y) (thus, x, y P(x, y)) – x y P(x, y) is equivalent to y x P(x, y) (thus x, y P(x, y))
 Mixing Quantifiers: Truth values Statement True when. . . False when. . . P(x, y) is true for every x y P(x, y) pair x, y There is at least one pair x, y for which P(x, y) is false x y P(x, y) For every x, there is a y for which P(x, y) is true There is an x for which P(x, y) is false for every y x y P(x, y) There is an x for which P(x, y) is true for every y For every x, there is a y for which P(x, y) is false x y. P(x, y) There is at least one pair P(x, y) is false for every pair x, y for which P(x, y) is true x, y
Mixing Quantifiers: Truth values Statement True when. . . False when. . . P(x, y) is true for every x y P(x, y) pair x, y There is at least one pair x, y for which P(x, y) is false x y P(x, y) For every x, there is a y for which P(x, y) is true There is an x for which P(x, y) is false for every y x y P(x, y) There is an x for which P(x, y) is true for every y For every x, there is a y for which P(x, y) is false x y. P(x, y) There is at least one pair P(x, y) is false for every pair x, y for which P(x, y) is true x, y
 Mixing Quantifiers: Example (1) • Express, in predicate logic, the statement that there is an infinite number of integers • Answer: ‒ Let P(x, y) be the statement that x
Mixing Quantifiers: Example (1) • Express, in predicate logic, the statement that there is an infinite number of integers • Answer: ‒ Let P(x, y) be the statement that x
 Mixing Quantifiers: Example (2) • Express the commutative law of addition for R • We want to express that for every pair of reals, x, y, the following holds: x+y=y+x • Answer: ‒Let P(x, y) be the statement that x+y ‒ Let the universe of discourse be the reals, R ‒ The statement can be expressed by the following x y (P(x, y) P(y, x)) Alternatively, x y (x+y = y+x)
Mixing Quantifiers: Example (2) • Express the commutative law of addition for R • We want to express that for every pair of reals, x, y, the following holds: x+y=y+x • Answer: ‒Let P(x, y) be the statement that x+y ‒ Let the universe of discourse be the reals, R ‒ The statement can be expressed by the following x y (P(x, y) P(y, x)) Alternatively, x y (x+y = y+x)
 Mixing Quantifiers: Example (3) • Express the multiplicative law for nonzero reals R {0} • We want to express that for every real number x, there exists a real number y such that xy=1 • Answer: x y (xy = 1)
Mixing Quantifiers: Example (3) • Express the multiplicative law for nonzero reals R {0} • We want to express that for every real number x, there exists a real number y such that xy=1 • Answer: x y (xy = 1)
 Mixing Quantifiers: Example (4) false mathematical statement • Does commutativity for substraction hold over the reals? • That is: does x-y=y-x for all pairs x, y in R? • Express using quantifiers x y (x-y = y-x)
Mixing Quantifiers: Example (4) false mathematical statement • Does commutativity for substraction hold over the reals? • That is: does x-y=y-x for all pairs x, y in R? • Express using quantifiers x y (x-y = y-x)
 Mixing Quantifiers: Example (5) • Express the statement as a logical expression: “There is a number x such that when it is added to any number, the result is that number and if it is multiplied by any number, the result is x” as a logical expression • Answer: • • Let P(x, y) be the expression “x+y=y” Let Q(x, y) be the expression “xy=x” The universe of discourse is N, Z, R, Q (but not Z+) Then the expression is: x y P(x, y) Q(x, y) Alternatively: x y (x+y=y) (xy = x)
Mixing Quantifiers: Example (5) • Express the statement as a logical expression: “There is a number x such that when it is added to any number, the result is that number and if it is multiplied by any number, the result is x” as a logical expression • Answer: • • Let P(x, y) be the expression “x+y=y” Let Q(x, y) be the expression “xy=x” The universe of discourse is N, Z, R, Q (but not Z+) Then the expression is: x y P(x, y) Q(x, y) Alternatively: x y (x+y=y) (xy = x)
 Outline • Introduction • Terminology: – Propositional functions; arguments; arity; universe of discourse • Quantifiers – Definition; using, mixing, biding, negating them • Logic Programming (Prolog) • Transcribing English to Logic • More exercises
Outline • Introduction • Terminology: – Propositional functions; arguments; arity; universe of discourse • Quantifiers – Definition; using, mixing, biding, negating them • Logic Programming (Prolog) • Transcribing English to Logic • More exercises
 Binding Variables • When a quantifier is used on a variable x, we say that x is bound • If no quantifier is used on a variable in a predicate statement, the variable is called free • Examples – In x y. P(x, y), both x and y are bound – In x. P(x, y), x is bound but y is free • A statement is called a well-formed formula, when all variables are properly quantified
Binding Variables • When a quantifier is used on a variable x, we say that x is bound • If no quantifier is used on a variable in a predicate statement, the variable is called free • Examples – In x y. P(x, y), both x and y are bound – In x. P(x, y), x is bound but y is free • A statement is called a well-formed formula, when all variables are properly quantified
 Binding Variables: Scope • The set of all variables bound by a common quantifier is called the scope of the quantifier • For example, in the expression x, y z. P(x, y, z, c) – What is the scope of existential quantifier? – What is the scope of universal quantifier? – What are the bound variables? – What are the free variables? – Is the expression a well-formed formula?
Binding Variables: Scope • The set of all variables bound by a common quantifier is called the scope of the quantifier • For example, in the expression x, y z. P(x, y, z, c) – What is the scope of existential quantifier? – What is the scope of universal quantifier? – What are the bound variables? – What are the free variables? – Is the expression a well-formed formula?
 Negation • We can use negation with quantified expressions as we used them with propositions • Lemma: Let P(x) be a predicate. Then the followings hold: ( x P(x)) x P(x) • This is essentially the quantified version of De Morgan’s Law (when the universe of discourse is finite, this is exactly De Morgan’s Law)
Negation • We can use negation with quantified expressions as we used them with propositions • Lemma: Let P(x) be a predicate. Then the followings hold: ( x P(x)) x P(x) • This is essentially the quantified version of De Morgan’s Law (when the universe of discourse is finite, this is exactly De Morgan’s Law)
 Negation: Truth Values of Negated Quantifiers Statement True when… x P(x) is false for every x x P(x) False when. . . There is an x for which P(x) is true x P(x) There is an x for which x P(x) is false P(x) is true for every x
Negation: Truth Values of Negated Quantifiers Statement True when… x P(x) is false for every x x P(x) False when. . . There is an x for which P(x) is true x P(x) There is an x for which x P(x) is false P(x) is true for every x
 Outline • Introduction • Terminology: – Propositional functions; arguments; arity; universe of discourse • Quantifiers – Definition; using, mixing, negating them • Logic Programming (Prolog) • Transcribing English to Logic • More exercises
Outline • Introduction • Terminology: – Propositional functions; arguments; arity; universe of discourse • Quantifiers – Definition; using, mixing, negating them • Logic Programming (Prolog) • Transcribing English to Logic • More exercises
 Prolog (1) • Prolog (Programming in Logic) is a programming language based on (a restricted form of) Predicate Logic (a. k. a. Predicate Calculus and FOL) • It was developed by the logicians of the Artificial Intelligence community for symbolic reasoning
Prolog (1) • Prolog (Programming in Logic) is a programming language based on (a restricted form of) Predicate Logic (a. k. a. Predicate Calculus and FOL) • It was developed by the logicians of the Artificial Intelligence community for symbolic reasoning
 Prolog (2) • Prolog allows the users to express facts and rules • Facts are propositional functions: student(mia), enrolled(mia, cse 235), instructor(patel, cse 235), etc. • Rules are implications with conjunctions: teaches(X, Y) : - instructor(X, Z), enrolled(Y, Z) • Prolog answers queries such as: ? enrolled(mia, cse 235) ? enrolled(X, cse 476) ? teaches(X, mia) by binding variables and doing theorem proving (i. e. , applying inference rules) as we will see in Section 1. 5
Prolog (2) • Prolog allows the users to express facts and rules • Facts are propositional functions: student(mia), enrolled(mia, cse 235), instructor(patel, cse 235), etc. • Rules are implications with conjunctions: teaches(X, Y) : - instructor(X, Z), enrolled(Y, Z) • Prolog answers queries such as: ? enrolled(mia, cse 235) ? enrolled(X, cse 476) ? teaches(X, mia) by binding variables and doing theorem proving (i. e. , applying inference rules) as we will see in Section 1. 5
 English into Logic • Logic is more precise than English • Transcribing English into Logic and vice versa can be tricky • When writing statements with quantifiers, usually the correct meaning is conveyed with the following combinations: Use with x Lion(x) Fierce(x): Every lion is fierce x Lion(x) Fierce(x): Everyone is a lion and everyone is fierce Use with x Lion(x) Vegan(x): Holds when you have at least one vegan lion x Lion(x) Vegan(x): Holds when you have vegan people in the universe of discourse (even though there is no vegan lion in the universe of discourse )
English into Logic • Logic is more precise than English • Transcribing English into Logic and vice versa can be tricky • When writing statements with quantifiers, usually the correct meaning is conveyed with the following combinations: Use with x Lion(x) Fierce(x): Every lion is fierce x Lion(x) Fierce(x): Everyone is a lion and everyone is fierce Use with x Lion(x) Vegan(x): Holds when you have at least one vegan lion x Lion(x) Vegan(x): Holds when you have vegan people in the universe of discourse (even though there is no vegan lion in the universe of discourse )
 More exercises (1) • Rewrite the following expression, pushing negation inward: x ( y z P(x, y, z) z y P(x, y, z)) • Answer: x ( y z P(x, y, z) z y P(x, y, z))
More exercises (1) • Rewrite the following expression, pushing negation inward: x ( y z P(x, y, z) z y P(x, y, z)) • Answer: x ( y z P(x, y, z) z y P(x, y, z))
 More Exercises (2) • Let P(x, y) denote ‘x is a factor of y’ where – x {1, 2, 3, …} and y {2, 3, 4, …} • Let Q(x, y) denote: – x, y [P(x, y) (x=1)] • Question: When is Q(x, y) true?
More Exercises (2) • Let P(x, y) denote ‘x is a factor of y’ where – x {1, 2, 3, …} and y {2, 3, 4, …} • Let Q(x, y) denote: – x, y [P(x, y) (x=1)] • Question: When is Q(x, y) true?
 Alert… • Some students wonder if: x, y P(x, y) ( x P(x, y)) ( y P(x, y)) • This is certainly not true. – In the left-hand side, both x, y are bound. – In the right-hand side, • In the first predicate, x is bound and y is free • In the second predicate, y is bound and x is free • Thus, the left-hand side is a proposition, but the right-hand side is not. They cannot be equivalent • All variables that occur in a propositional function must be bound to turn it into a proposition
Alert… • Some students wonder if: x, y P(x, y) ( x P(x, y)) ( y P(x, y)) • This is certainly not true. – In the left-hand side, both x, y are bound. – In the right-hand side, • In the first predicate, x is bound and y is free • In the second predicate, y is bound and x is free • Thus, the left-hand side is a proposition, but the right-hand side is not. They cannot be equivalent • All variables that occur in a propositional function must be bound to turn it into a proposition
 Rules of Inference
Rules of Inference
 Proofs in mathematics are valid arguments An argument is a sequence of statements that end in a conclusion By valid we mean the conclusion must follow from the truth of the preceding statements or premises We use rules of inference to construct valid arguments
Proofs in mathematics are valid arguments An argument is a sequence of statements that end in a conclusion By valid we mean the conclusion must follow from the truth of the preceding statements or premises We use rules of inference to construct valid arguments
 Valid Arguments in Propositional Logic Is this a valid argument? If you listen you will hear what I’m saying You are listening Therefore, you hear what I am saying Let p represent the statement “you listen” Let q represent the statement “you hear what I am saying” The argument has the form:
Valid Arguments in Propositional Logic Is this a valid argument? If you listen you will hear what I’m saying You are listening Therefore, you hear what I am saying Let p represent the statement “you listen” Let q represent the statement “you hear what I am saying” The argument has the form:
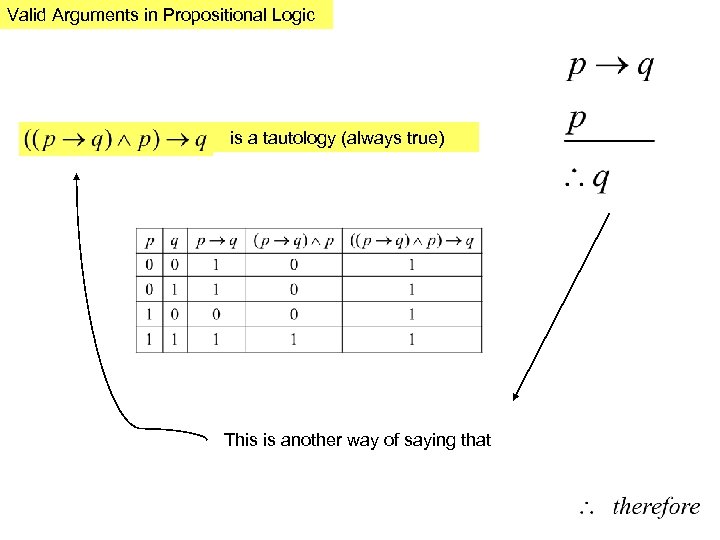 Valid Arguments in Propositional Logic is a tautology (always true) This is another way of saying that
Valid Arguments in Propositional Logic is a tautology (always true) This is another way of saying that
 Valid Arguments in Propositional Logic When we replace statements/propositions with propositional variables we have an argument form. Defn: An argument (in propositional logic) is a sequence of propositions. All but the final proposition are called premises. The last proposition is the conclusion The argument is valid iff the truth of all premises implies the conclusion is true An argument form is a sequence of compound propositions
Valid Arguments in Propositional Logic When we replace statements/propositions with propositional variables we have an argument form. Defn: An argument (in propositional logic) is a sequence of propositions. All but the final proposition are called premises. The last proposition is the conclusion The argument is valid iff the truth of all premises implies the conclusion is true An argument form is a sequence of compound propositions
 Valid Arguments in Propositional Logic The argument form with premises and conclusion is valid when is a tautology We prove that an argument form is valid by using the laws of inference But we could use a truth table. Why not?
Valid Arguments in Propositional Logic The argument form with premises and conclusion is valid when is a tautology We prove that an argument form is valid by using the laws of inference But we could use a truth table. Why not?
 Rules of Inference for Propositional Logic modus ponens aka law of detachment modus ponens (Latin) translates to “mode that affirms” The 1 st law
Rules of Inference for Propositional Logic modus ponens aka law of detachment modus ponens (Latin) translates to “mode that affirms” The 1 st law
 Rules of Inference for Propositional Logic modus ponens If it’s a nice day we’ll go to the beach. Assume the hypothesis “it’s a nice day” is true. Then by modus ponens it follows that “we’ll go to the beach”.
Rules of Inference for Propositional Logic modus ponens If it’s a nice day we’ll go to the beach. Assume the hypothesis “it’s a nice day” is true. Then by modus ponens it follows that “we’ll go to the beach”.
 Rules of Inference for Propositional Logic A valid argument can lead to an incorrect conclusion if one of its premises is wrong/false! modus ponens
Rules of Inference for Propositional Logic A valid argument can lead to an incorrect conclusion if one of its premises is wrong/false! modus ponens
 Rules of Inference for Propositional Logic A valid argument can lead to an incorrect conclusion if one of its premises is wrong/false! The argument is valid as it is constructed using modus ponens But one of the premises is false (p is false) So, we cannot derive the conclusion modus ponens
Rules of Inference for Propositional Logic A valid argument can lead to an incorrect conclusion if one of its premises is wrong/false! The argument is valid as it is constructed using modus ponens But one of the premises is false (p is false) So, we cannot derive the conclusion modus ponens
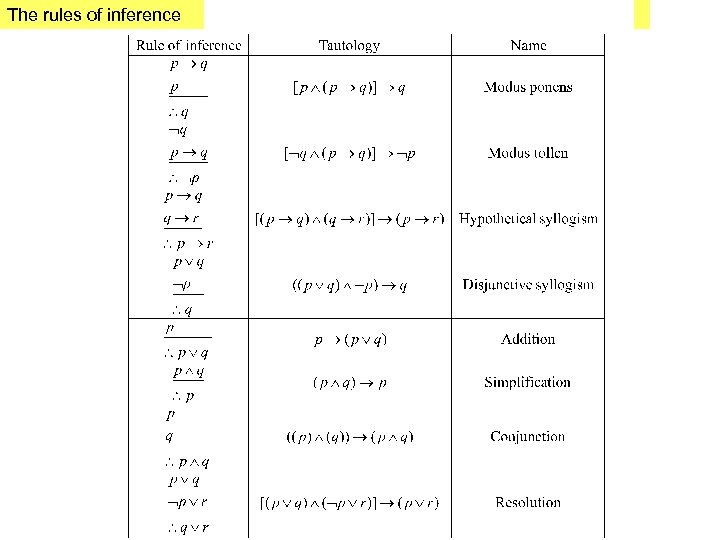 The rules of inference
The rules of inference
 Another view on what we are doing You might think of this as some sort of game. You are given some statement, and you want to see if it is a valid argument and true You translate the statement into argument form using propositional variables, and make sure you have the premises right, and clear what is the conclusion You then want to get from premises/hypotheses (A) to the conclusion (B) using the rules of inference. So, get from A to B using as “moves” the rules of inference
Another view on what we are doing You might think of this as some sort of game. You are given some statement, and you want to see if it is a valid argument and true You translate the statement into argument form using propositional variables, and make sure you have the premises right, and clear what is the conclusion You then want to get from premises/hypotheses (A) to the conclusion (B) using the rules of inference. So, get from A to B using as “moves” the rules of inference
 Using the rules of inference to build arguments It is not sunny this afternoon and it is colder than yesterday. If we go swimming it is sunny. If we do not go swimming then we will take a canoe trip. If we take a canoe trip then we will be home by sunset. We will be home by sunset An example
Using the rules of inference to build arguments It is not sunny this afternoon and it is colder than yesterday. If we go swimming it is sunny. If we do not go swimming then we will take a canoe trip. If we take a canoe trip then we will be home by sunset. We will be home by sunset An example
 Using the rules of inference to build arguments 1. 2. 3. 4. 5. An example It is not sunny this afternoon and it is colder than yesterday. If we go swimming it is sunny. If we do not go swimming then we will take a canoe trip. If we take a canoe trip then we will be home by sunset. We will be home by sunset propositions hypotheses
Using the rules of inference to build arguments 1. 2. 3. 4. 5. An example It is not sunny this afternoon and it is colder than yesterday. If we go swimming it is sunny. If we do not go swimming then we will take a canoe trip. If we take a canoe trip then we will be home by sunset. We will be home by sunset propositions hypotheses
 Using the rules of inference to build arguments An example
Using the rules of inference to build arguments An example
 Using the resolution rule (an example) 1. Anna is skiing or it is not snowing. 2. It is snowing or Bart is playing hockey. 3. Consequently Anna is skiing or Bart is playing hockey. We want to show that (3) follows from (1) and (2)
Using the resolution rule (an example) 1. Anna is skiing or it is not snowing. 2. It is snowing or Bart is playing hockey. 3. Consequently Anna is skiing or Bart is playing hockey. We want to show that (3) follows from (1) and (2)
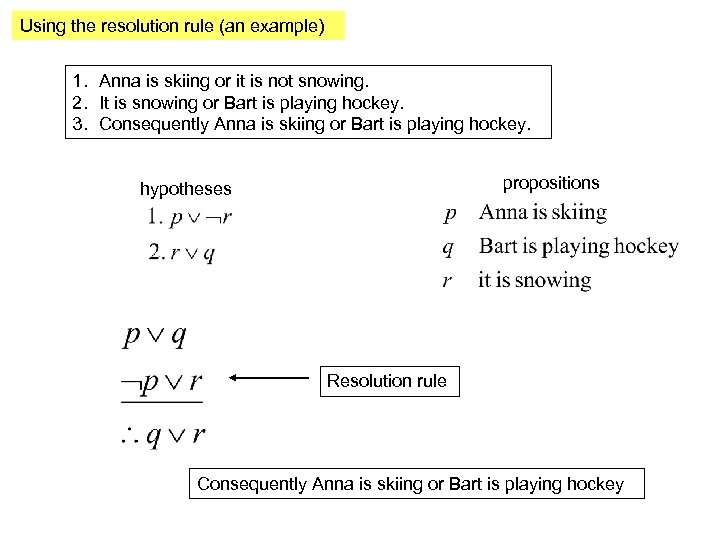 Using the resolution rule (an example) 1. Anna is skiing or it is not snowing. 2. It is snowing or Bart is playing hockey. 3. Consequently Anna is skiing or Bart is playing hockey. propositions hypotheses Resolution rule Consequently Anna is skiing or Bart is playing hockey
Using the resolution rule (an example) 1. Anna is skiing or it is not snowing. 2. It is snowing or Bart is playing hockey. 3. Consequently Anna is skiing or Bart is playing hockey. propositions hypotheses Resolution rule Consequently Anna is skiing or Bart is playing hockey
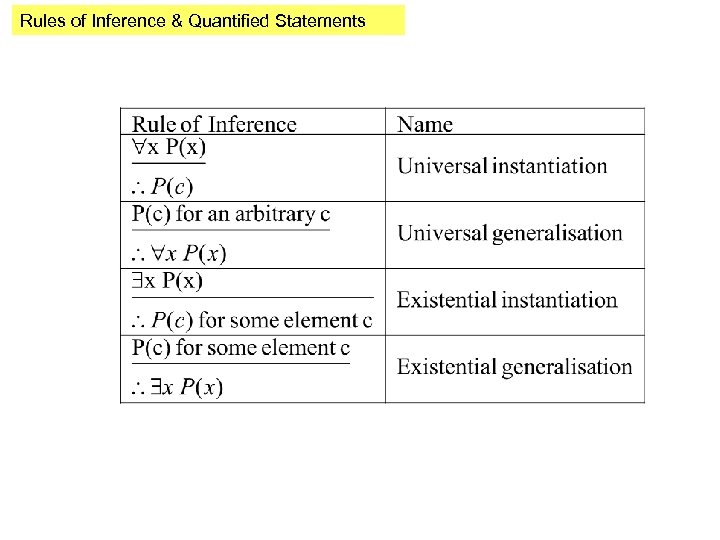
 Rules of Inference & Quantified Statements All men are £$%^$*(%, said Jane John is a man Therefore John is a £$%^$*( Above is an example of a rule called “Universal Instantiation”. We conclude P(c) is true, where c is a particular/named element in the domain of discourse, given the premise
Rules of Inference & Quantified Statements All men are £$%^$*(%, said Jane John is a man Therefore John is a £$%^$*( Above is an example of a rule called “Universal Instantiation”. We conclude P(c) is true, where c is a particular/named element in the domain of discourse, given the premise
 Rules of Inference & Quantified Statements
Rules of Inference & Quantified Statements
 Rules of Inference & Quantified Statements All men are £$%^$*(%, said Jane John is a man Therefore John is a £$%^$*( premises
Rules of Inference & Quantified Statements All men are £$%^$*(%, said Jane John is a man Therefore John is a £$%^$*( premises
 Rules of Inference & Quantified Statements Maybe another example?
Rules of Inference & Quantified Statements Maybe another example?


