Uniform Sampling from the Web via Random Walks

Uniform Sampling from the Web via Random Walks Ziv Bar-Yossef Alexander Berg Steve Chien Jittat Fakcharoenphol Dror Weitz University of California at Berkeley 1

Motivation: Web Measurements • Main goal: Develop a cheap method to sample uniformly from the Web • Use a random sample of web pages to approximate: – – – search engine coverage domain name distribution (. com, . org, . edu) percentage of porn pages average number of links in a page average page length • Note: A web page is a static html page 2

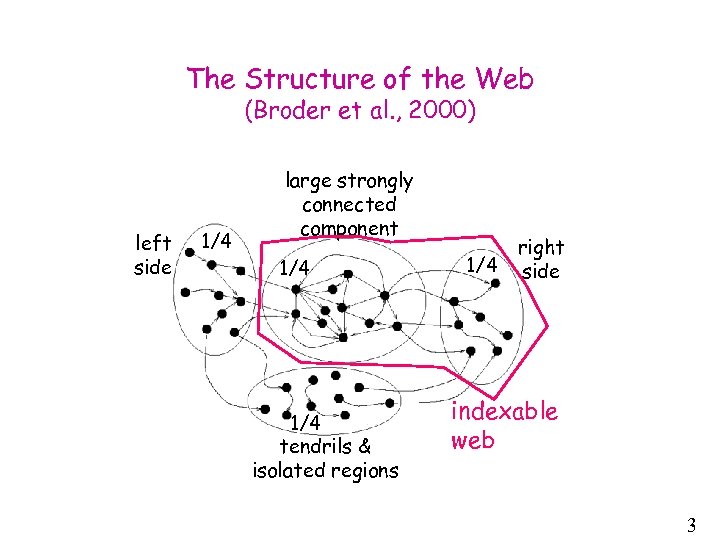
The Structure of the Web (Broder et al. , 2000) left side 1/4 large strongly connected component 1/4 tendrils & isolated regions right 1/4 side indexable web 3

Why is Web Sampling Hard? • Obvious solution: sample from an index of all pages • Maintaining an index of Web pages is difficult – Requires extensive resources (storage, bandwidth) – Hard to implement • There is no consistent index of all Web pages – Difficult to get complete coverage – Month to crawl/index most of the Web – Web is changing every minute 4

Our Approach: Random Walks for Random Sampling • Random walk on a graph provides a sample of nodes • Graph is undirected and regular sample is uniform – Problems: The Web is neither undirected nor regular • Our solution – Incrementally create an undirected regular graph with the same nodes as the Web – Perform the walk on this graph 5

Related Work • Monika Henzinger, et al. (2000) – Random walk produces pages distributed by Google’s page rank. – Weight these pages to produce a nearly uniform sample. • Krishna Bharat & Andrei Broder (1998) – Measured relative size and overlap of search engines using random queries. • Steve Lawrence & Lee Giles (1998, 1999) – Size of the web by probing IP addresses and crawling servers. – Search engine coverage in response to certain queries. 6

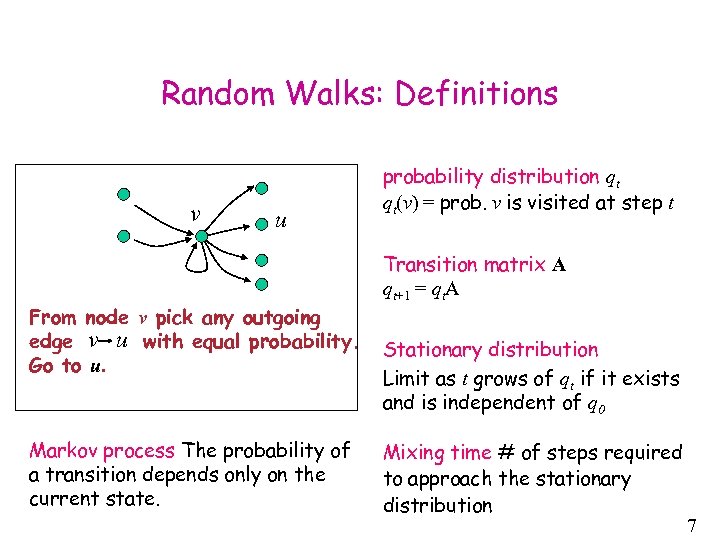
Random Walks: Definitions v u From node v pick any outgoing edge v u with equal probability. Go to u. Markov process The probability of a transition depends only on the current state. probability distribution qt qt(v) = prob. v is visited at step t Transition matrix A qt+1 = qt. A Stationary distribution Limit as t grows of qt if it exists and is independent of q 0 Mixing time # of steps required to approach the stationary distribution 7

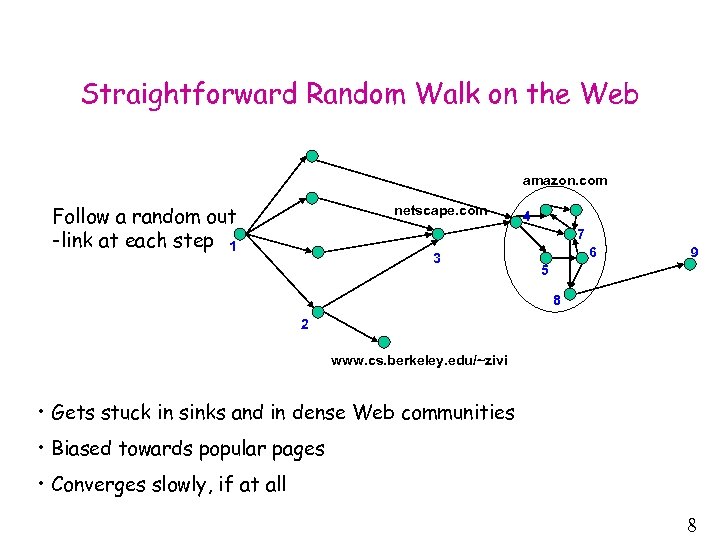
Straightforward Random Walk on the Web amazon. com Follow a random out -link at each step 1 netscape. com 4 7 3 6 9 5 8 2 www. cs. berkeley. edu/~zivi • Gets stuck in sinks and in dense Web communities • Biased towards popular pages • Converges slowly, if at all 8

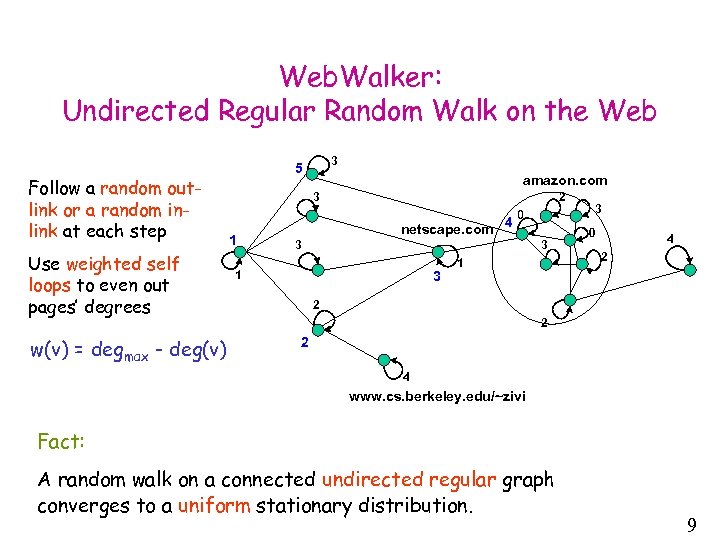
Web. Walker: Undirected Regular Random Walk on the Web Follow a random outlink or a random inlink at each step Use weighted self loops to even out pages’ degrees w(v) = degmax - deg(v) 3 5 amazon. com 3 1 2 netscape. com 4 0 3 3 1 3 0 4 2 2 4 www. cs. berkeley. edu/~zivi Fact: A random walk on a connected undirected regular graph converges to a uniform stationary distribution. 9

Web. Walker: Mixing Time Theorem [Markov chain folklore]: A random walk’s mixing time is at most log(N)/(1 - 2) where N = size of the graph 1 - 2 = eigenvalue gap of the transition matrix Experiment (using an extensive Alexa crawl of the web from 1996) Web. Walker’s eigenvalue gap: 1 - 2 10 -5 Result: Webwalker’s mixing time is 3. 1 million steps • Self loop steps are free • Only 1 in 30, 000 steps is not a self loop step (degmax 3 x 105, degavg= 10) Result: Webwalker’s actual mixing time is only 100 steps! 10

Web. Walker: Mixing Time (cont. ) • Mixing time on the current Web may be similar – Some evidence that the structure of the Web today is similar to the structure in 1996 (Kumar et al. , 1999, Broder et al. , 2000) 11

Web. Walker: Realization (1) Webwalker(v): • Spend expected degmax/deg(v) steps at v • Pick a random link incident to v (either v u or u v) • Webwalker(u) Problems • The in-links of v are not available • deg(v) is not available Partial sources of in-links: • Previously visited nodes • Reverse link services of search engines 12

Web. Walker: Realization (2) • Web. Walker uses only available links: – out-links – in-links from previously visited pages – first r in-links returned from the search engines • Web. Walker walks on a sub-graph of the Web – sub-graph induced by available links – to ensure consistency: as soon as a page is visited its incident edge list is fixed for the rest of the walk 13

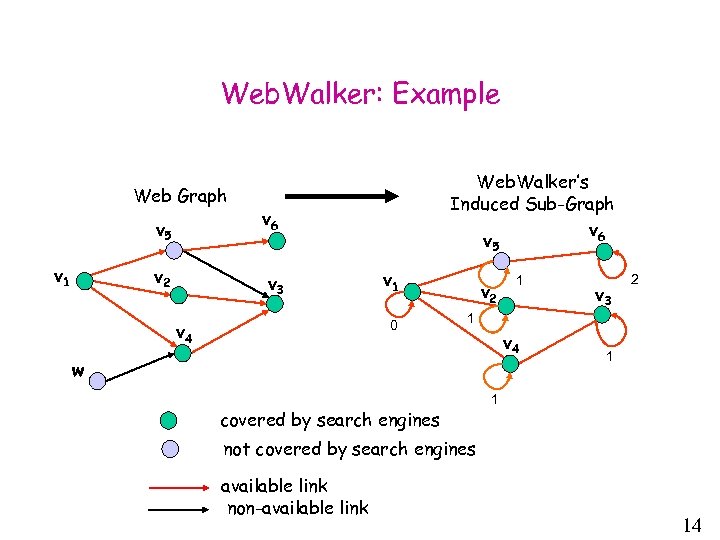
Web. Walker: Example Web Graph v 5 v 1 v 2 Web. Walker’s Induced Sub-Graph v 6 v 5 v 6 v 3 v 1 0 v 4 v 2 1 v 3 2 1 v 4 w covered by search engines 1 1 not covered by search engines available link non-available link 14

Web. Walker: Bad News • Web. Walker becomes a true random walk only after its induced sub-graph “stabilizes” • Induced sub-graph is random • Induced sub-graph misses some of the nodes • Eigenvalue gap analysis does not hold anymore 15

Web. Walker: Good News • Web. Walker eventually converges to a uniform distribution on the nodes of its induced sub-graph • Web. Walker is a “close approximation” of a random walk much before the sub-graph stabilizes • Theorem: Web. Walker’s induced sub-graph is guaranteed to eventually cover the whole indexable Web. • Corollary: Web. Walker can produce uniform samples from the indexable Web. 16

Evaluation of Web. Walker’s Performance Questions to address in experiments: • Structure of induced sub-graphs • Mixing time • Potential bias in early stages of the walk: – towards high degree pages – towards the search engines – towards the starting page’s neighborhood 17

Web. Walker: Evaluation Experiments • Run Web. Walker on the 1996 copy of the Web – 37. 5 million pages – 15 million indexable pages – degavg= 7. 15 – degmax= 300, 000 • Designate a fraction p of the pages as the search engine index • Use Web. Walker to generate a sample of 100, 000 pages • Check the resulting sample against the actual values 18

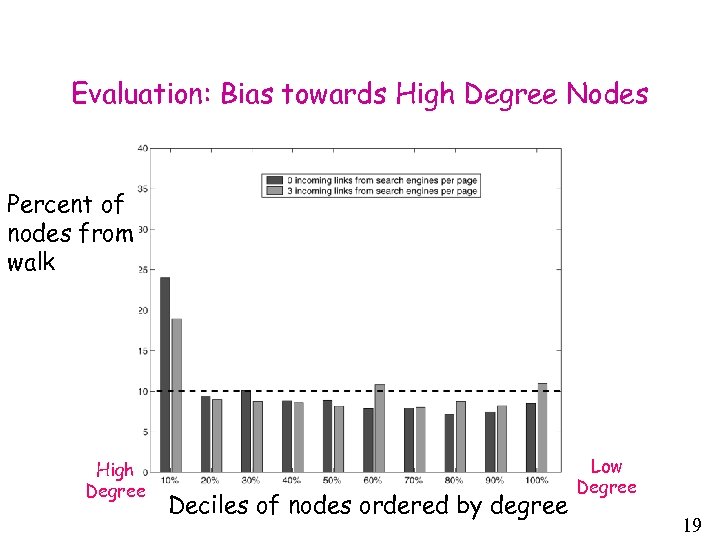
Evaluation: Bias towards High Degree Nodes Percent of nodes from walk High Degree Deciles of nodes ordered by degree Low Degree 19

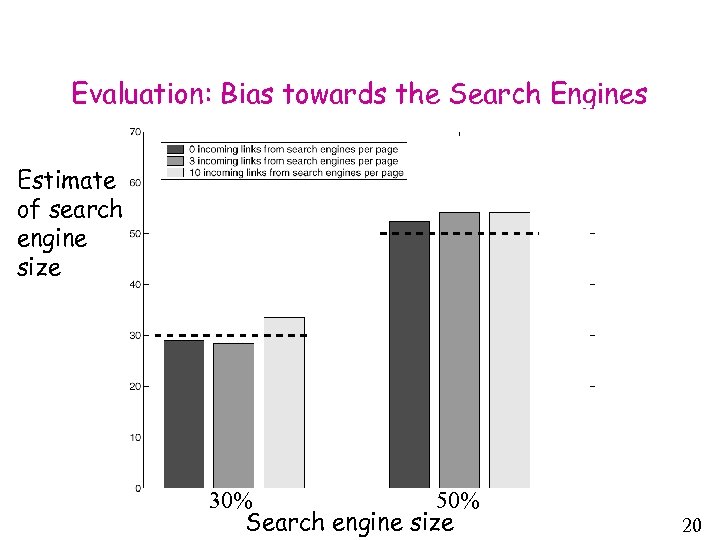
Evaluation: Bias towards the Search Engines Estimate of search engine size 30% 50% Search engine size 20

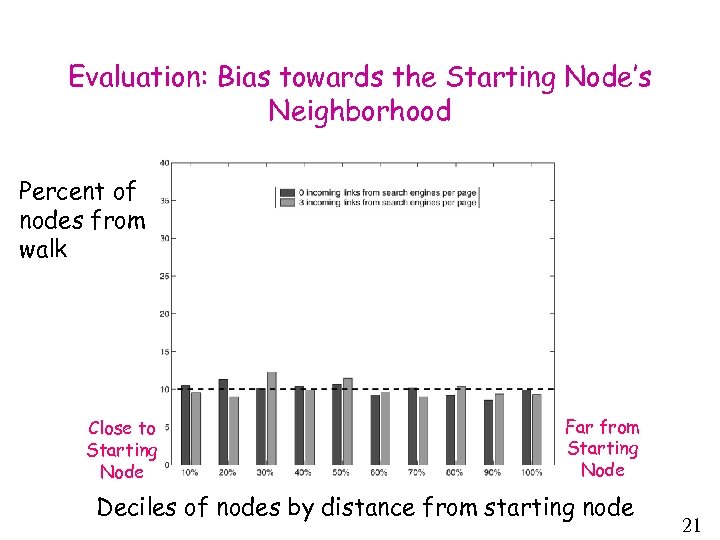
Evaluation: Bias towards the Starting Node’s Neighborhood Percent of nodes from walk Close to Starting Node Far from Starting Node Deciles of nodes by distance from starting node 21

Web. Walker: Experiments on the Web • Run Web. Walker on the actual Web • Two runs of 34, 000 pages each • Dates: July 8, 2000 - July 15, 2000 • Used four search engines for reversed links: • Alta. Vista, Hot. Bot, Lycos, Go 22

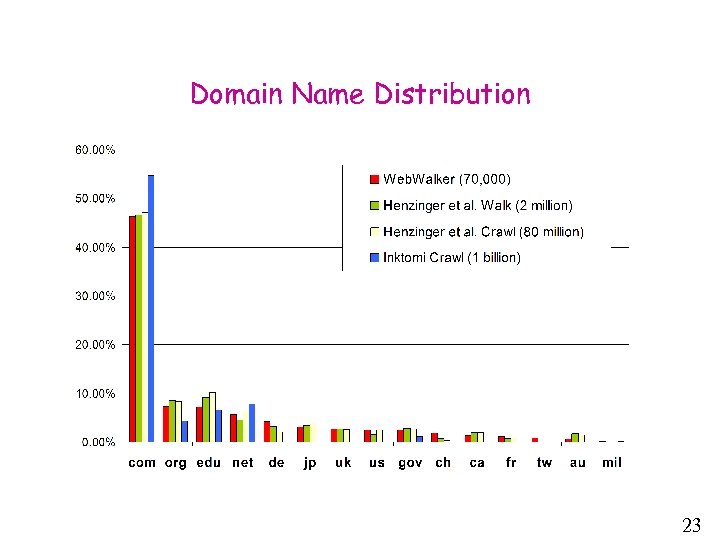
Domain Name Distribution 23

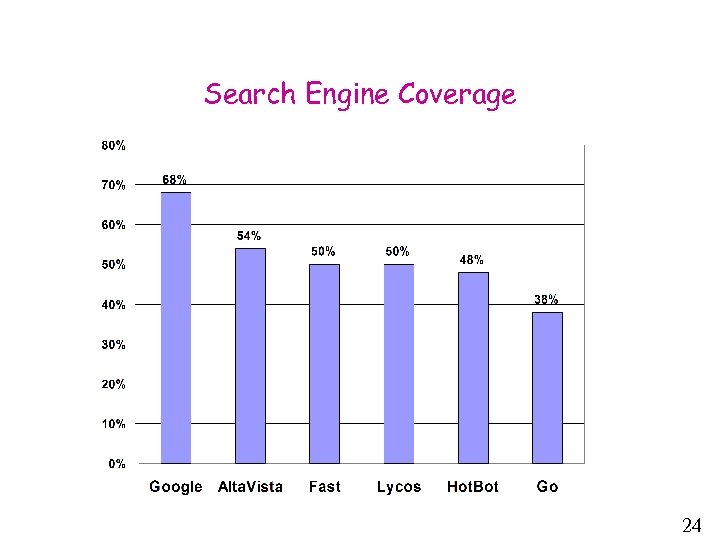
Search Engine Coverage 24

Web Page Parameters • Average page size: 8, 390 Bytes • Average # of images on a page: 9. 3 Images • Average # of hyperlinks on a page: 15. 6 Links 25

Conclusions • Uniform sampling of Web pages by random walks • Good news: – walk provably converges to a uniform distribution – easy to implement and run with few resources – encouraging experimental results • Bad news: – no theoretical guarantees on the walk’s mixing time – some biases towards high degree nodes and the search engines • Future work: – obtain a better theoretical analysis – eliminate biases – deal with dynamic content 26

Thank You! 27