43d12cd62e5af6e7669b44e73ab9169f.ppt
- Количество слайдов: 11

Understanding Probability and Long-Term Expectations Are Coincidences Improbable? Example from Student - Kalyani Thampi I have an example of "chance" that I thought about mentioning in class but we didn't have enough time. Recently, I've been receiving letters from collection agencies telling me that I owe X amount of money on a couple of credit cards at stores where I shop. However, I have never once fallen behind on payments so I couldn't understand why/how I would be so far in debt with these stores as to be sent to collection agencies! After a few weeks of investigation (calling my bank, agency, stores, etc), I solved the mystery: apparently, there is another Kalyani Thampi who lives on the upper west side on Amsterdam Avenue with almost the same address, and the stores and collection agencies got it wrong. Also, she uses the same bank as I do (as I found out later), so when she started paying the money, it came out of my account! What are the chances that we have the same name, live in the same neighborhood, shop at the same two stores and have the same bank? Kalyani Thampi is a rare name in the U. S. I'd say it's destiny but I wouldn't want to think that it was my fate to meet a girl with such awful financial literacy.
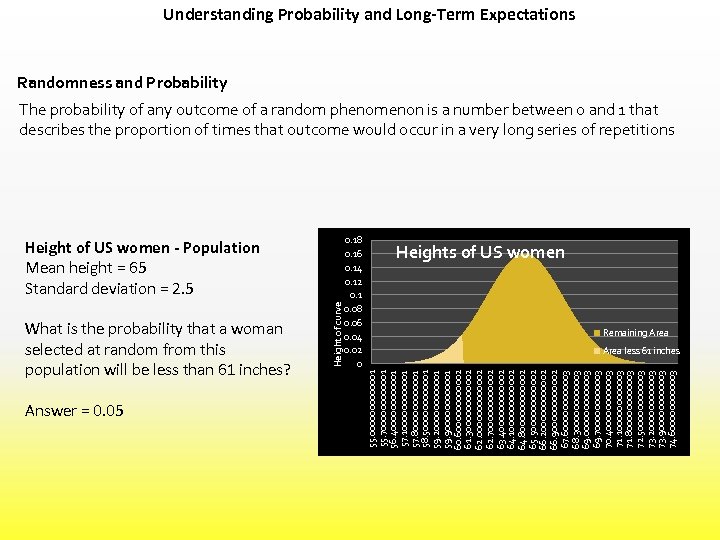
Understanding Probability and Long-Term Expectations Randomness and Probability The probability of any outcome of a random phenomenon is a number between 0 and 1 that describes the proportion of times that outcome would occur in a very long series of repetitions Answer = 0. 05 0. 18 0. 16 0. 14 0. 12 0. 1 0. 08 0. 06 0. 04 0. 02 0 Heights of US women Remaining Area less 61 inches 55. 0000001 55. 70000001 56. 40000001 57. 10000001 57. 80000001 58. 50000001 59. 20000001 59. 90000001 60. 60000002 61. 30000002 62. 70000002 63. 40000002 64. 10000002 64. 80000002 65. 50000002 66. 20000002 66. 90000002 67. 60000003 68. 30000003 69. 70000003 70. 40000003 71. 10000003 71. 80000003 72. 50000003 73. 20000003 73. 90000003 74. 60000003 What is the probability that a woman selected at random from this population will be less than 61 inches? Height of curve Height of US women - Population Mean height = 65 Standard deviation = 2. 5

Understanding Probability and Long-Term Expectations Probability What does the word probability mean? Two distinct interpretations: • For the probability of winning a lottery based on buying a single ticket -- we can quantify the chances exactly. • For the probability that we will eventually buy a home -- we are basing our assessment on personal beliefs about how life will evolve for us. The Relative-Frequency Interpretation Relative-frequency interpretation: applies to situations that can be repeated over and over again. Examples: • Buying a weekly lottery ticket and observing whether it is a winner. • Observing births and noting if baby is male or female.
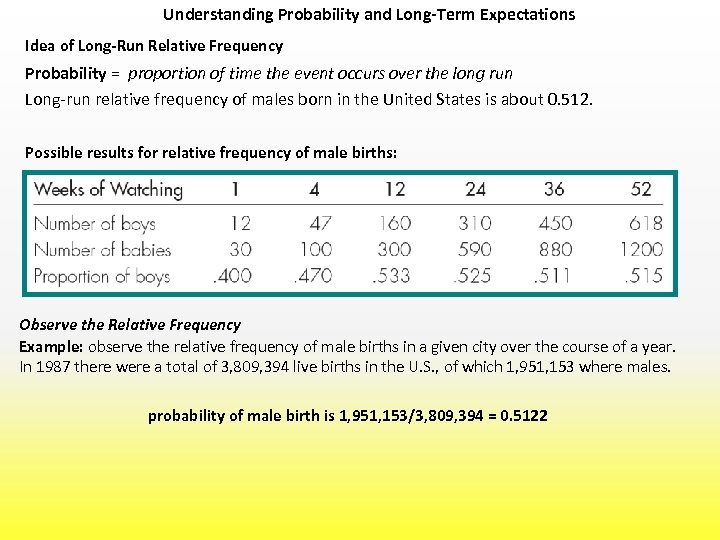
Understanding Probability and Long-Term Expectations Idea of Long-Run Relative Frequency Probability = proportion of time the event occurs over the long run Long-run relative frequency of males born in the United States is about 0. 512. Possible results for relative frequency of male births: Observe the Relative Frequency Example: observe the relative frequency of male births in a given city over the course of a year. In 1987 there were a total of 3, 809, 394 live births in the U. S. , of which 1, 951, 153 where males. probability of male birth is 1, 951, 153/3, 809, 394 = 0. 5122
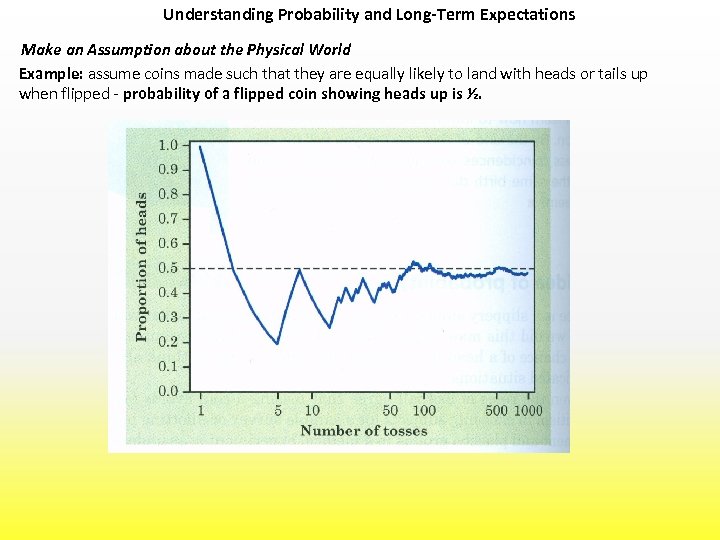
Understanding Probability and Long-Term Expectations Make an Assumption about the Physical World Example: assume coins made such that they are equally likely to land with heads or tails up when flipped - probability of a flipped coin showing heads up is ½.

Understanding Probability and Long-Term Expectations The Personal-Probability Interpretation Personal probability: the degree to which a given individual believes the event will happen. Personal-Probability versus Relative Frequency Probability
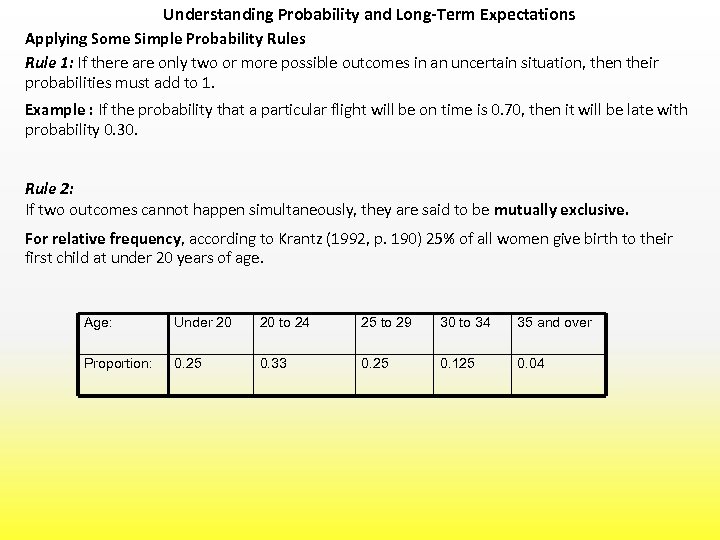
Understanding Probability and Long-Term Expectations Applying Some Simple Probability Rules Rule 1: If there are only two or more possible outcomes in an uncertain situation, then their probabilities must add to 1. Example : If the probability that a particular flight will be on time is 0. 70, then it will be late with probability 0. 30. Rule 2: If two outcomes cannot happen simultaneously, they are said to be mutually exclusive. For relative frequency, according to Krantz (1992, p. 190) 25% of all women give birth to their first child at under 20 years of age. Age: Under 20 20 to 24 25 to 29 30 to 34 35 and over Proportion: 0. 25 0. 33 0. 25 0. 125 0. 04

Understanding Probability and Long-Term Expectations Applying Some Simple Probability Rules Rule 3: If two events do not influence each other, and if knowledge about one doesn’t help with knowledge of the probability of the other, the events are said to be independent of each other. If two events are independent, the probability that they both happen is found by multiplying their individual probabilities. Example: Suppose for first-year students at your university the percentage is 20%. If these students are randomly assigned to dorm rooms, what is the probability that two people assigned to the same room are either both smokers or both nonsmokers? Independent Events? Event A is that it snows tomorrow; event B is that the high temperature tomorrow is at least 60 degrees Fahrenheit. You buy a lottery ticket, betting the same numbers two weeks in a row. Event A is that you win in the first week; event B is that you win in the second week. Event A is that a major earthquake will occur somewhere in the world next month; event B is that the Dow Jones Industrial Average will be higher next month

Understanding Probability and Long-Term Expectations Applying Some Simple Probability Rules Rule 4: If the ways in which one event can occur are a subset of those in which another event can occur, then the probability of the subset event cannot be higher than the probability of the one for which it is a subset. Text Question 12. A study by Kahneman and Tversky (1982, p. 496) asked people the following question: • Linda is 31 years old. single, outspoken, and very bright. She majored in philosophy. • As a student, she was deeply concerned with issues of discrimination and social justice and also participated in antinuclear demonstrations. Please check off the most likely alternative: A. Linda is a bank teller. B. Linda is a bank teller and is active in the feminist movement. Frequency Format versus Probability form Now let us change the question slightly without changing the description of Linda: Imagine women who fit the description of Linda How many of these women are bank tellers? How many of these women are bank tellers and active in the feminist movement?

Understanding Probability and Long-Term Expectations When Will It Happen? • Probability an outcome will occur on any given instance is p. • Probability the outcome will not occur is (1 – p). • Outcome each time is independent of outcome all other times. Probability it doesn’t occur on 1 st try but does occur on 2 nd try is (1 – p)p.
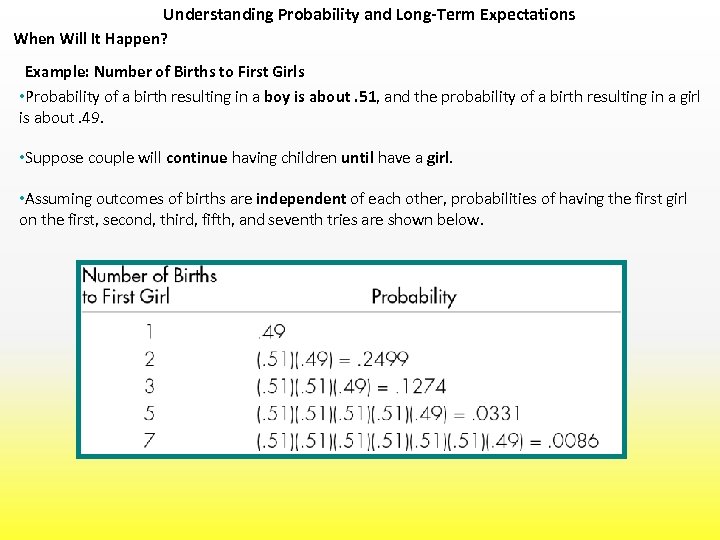
Understanding Probability and Long-Term Expectations When Will It Happen? Example: Number of Births to First Girls • Probability of a birth resulting in a boy is about. 51, and the probability of a birth resulting in a girl is about. 49. • Suppose couple will continue having children until have a girl. • Assuming outcomes of births are independent of each other, probabilities of having the first girl on the first, second, third, fifth, and seventh tries are shown below.
43d12cd62e5af6e7669b44e73ab9169f.ppt