Угол между векторами Скалярное произведение векторов Цели

Угол между векторами. Скалярное произведение векторов

Цели урока: • Ввести понятия угла между векторами и скалярного произведения векторов. • Рассмотреть формулу скалярного произведения в координатах. • Показать применение скалярного произведения векторов при решении задач.

Повторение: • Какие векторы называются равными? • Как найти длину вектора по координатам его начала и конца? В А • Какие векторы называются коллинеарными? или

Повторение. (Устно) Векторы в пространстве. 1) Дано: Найти: 2) Дано: Равны ли векторы и ? Нет, т. к. равные векторы имеют равные координаты. 3) Дано: ? Коллинеарны ли векторы Нет и ?

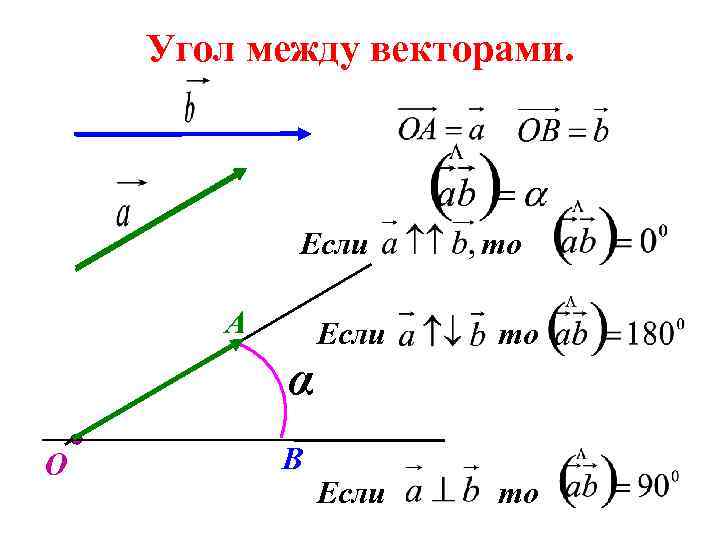Угол между векторами. Если А α О В то Если то

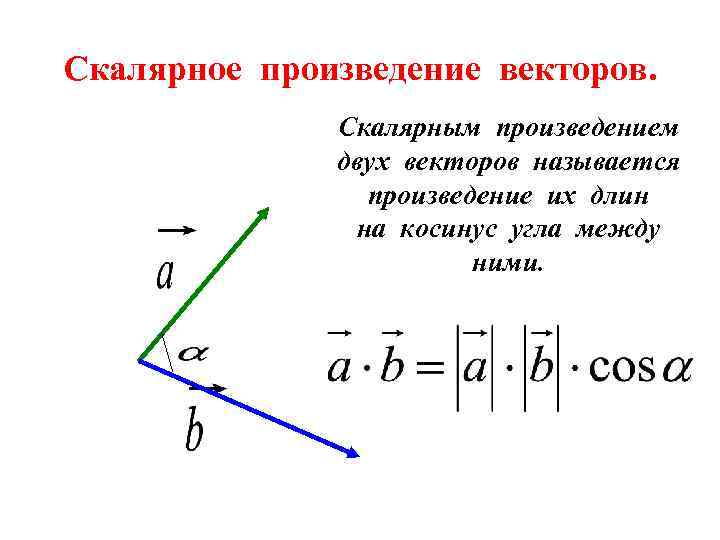Скалярное произведение векторов. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

Вспомним планиметрию… Если , то Скалярное произведение называется скалярным квадратом вектора

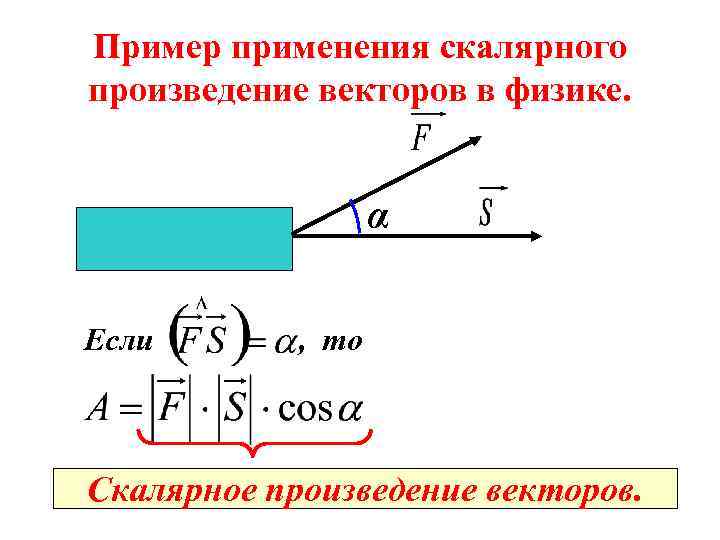Пример применения скалярного произведение векторов в физике. α Если , то Скалярное произведение векторов.

Формула скалярного произведения векторов в пространстве. Скалярное произведение двух векторов равно сумме произведений соответствующих координат этих векторов.

Косинус угла между ненулевыми векторами

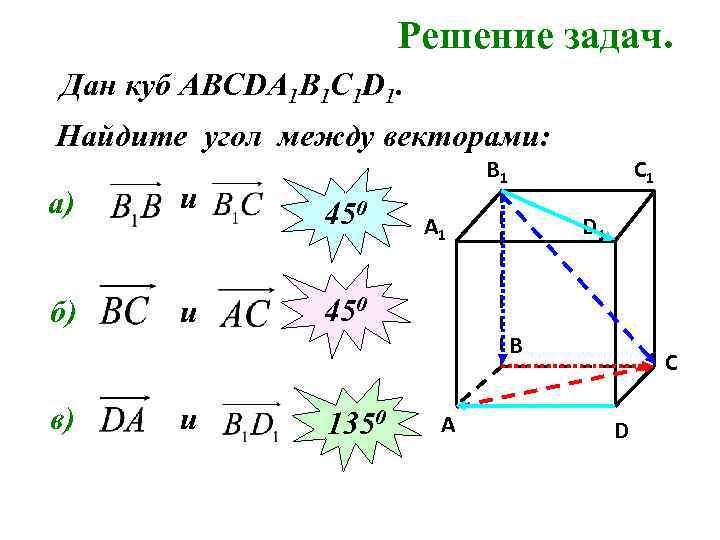Решение задач. Дан куб АВСDA 1 B 1 C 1 D 1. Найдите угол между векторами: B 1 а) и 450 б) и C 1 450 A 1 D 1 B в) и 1350 A C D

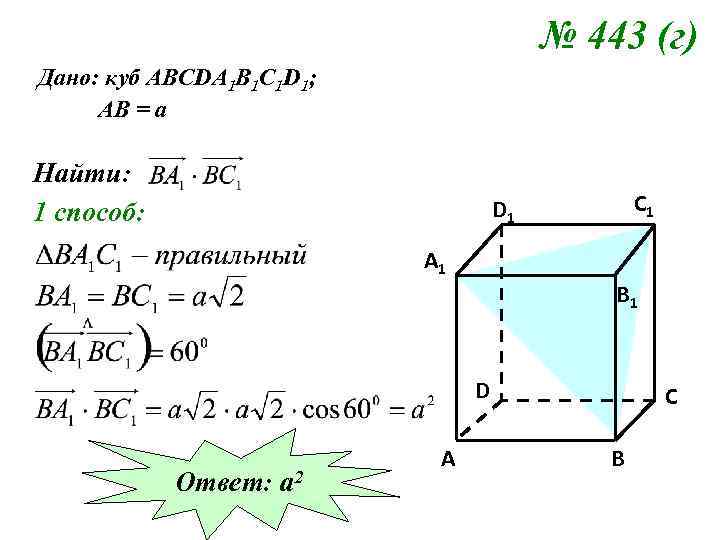№ 443 (г) Дано: куб АВСDA 1 B 1 C 1 D 1; АВ = а Найти: 1 способ: C 1 D 1 A 1 B 1 D Ответ: а 2 A C B

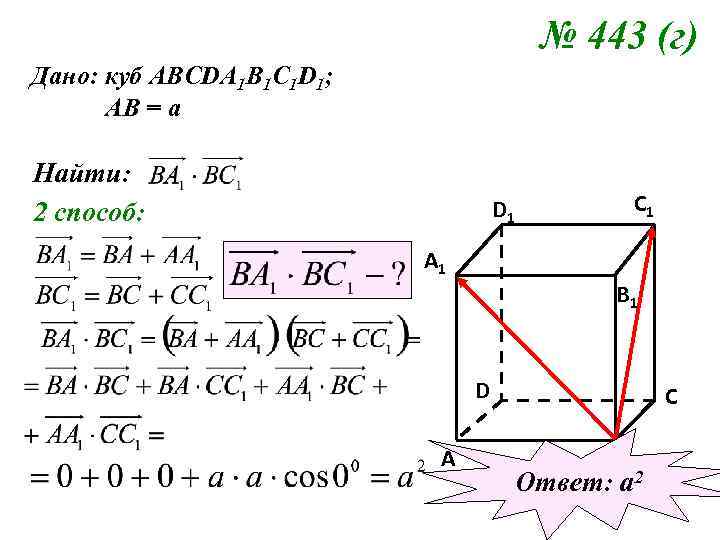№ 443 (г) Дано: куб АВСDA 1 B 1 C 1 D 1; АВ = а Найти: 2 способ: C 1 D 1 A 1 B 1 D A C B Ответ: а 2

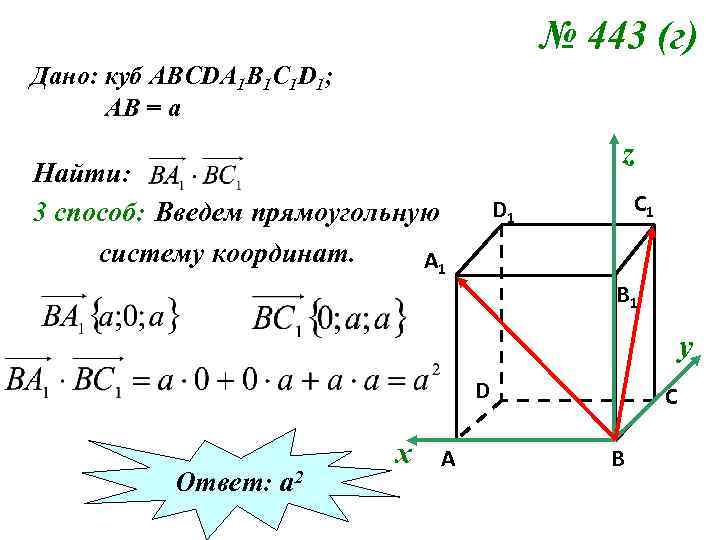№ 443 (г) Дано: куб АВСDA 1 B 1 C 1 D 1; АВ = а z Найти: 3 способ: Введем прямоугольную систему координат. A 1 C 1 D 1 B 1 у D Ответ: а 2 х A C B

Скалярное произведение векторов.