Угол между прямыми Любая прямая а лежащая

Зарегистрируйтесь, чтобы просмотреть полный документ!

Угол между прямыми.

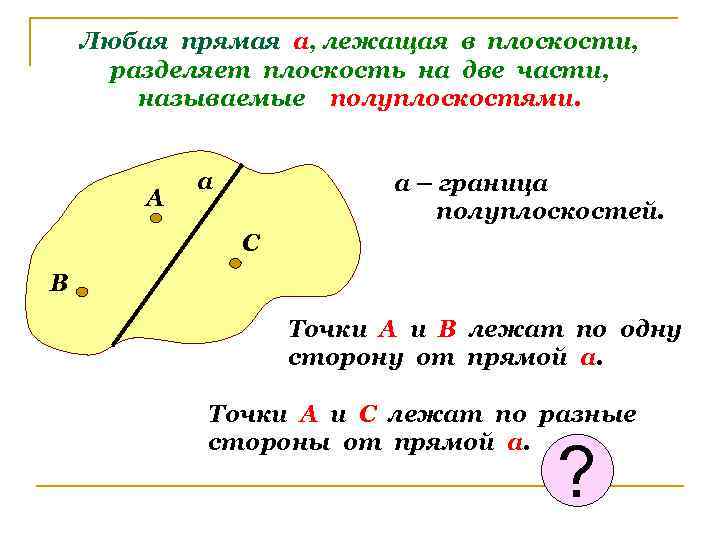
Любая прямая а, лежащая в плоскости, разделяет плоскость на две части, называемые полуплоскостями. А а а – граница полуплоскостей. С В Точки А и В лежат по одну сторону от прямой а. Точки А и С лежат по разные стороны от прямой а. ?

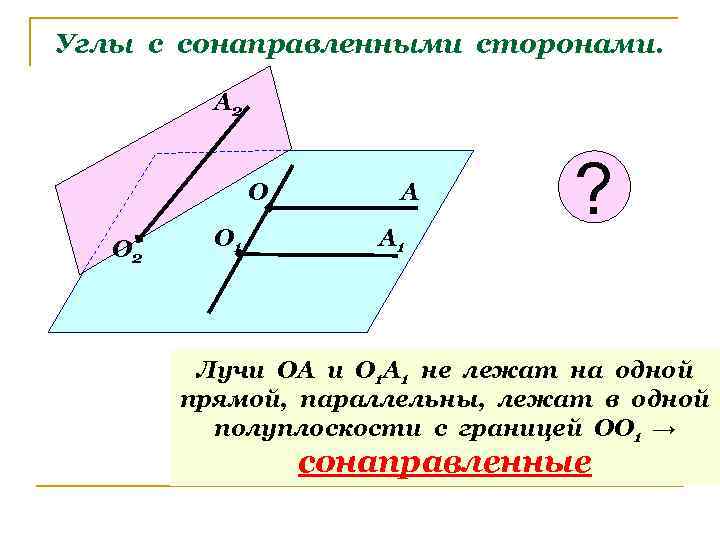
Углы с сонаправленными сторонами. А 2 О О 2 О 1 А А 1 ? Лучи ОА и О 1 А 1 не лежат на одной прямой, параллельны, лежат в одной полуплоскости с границей ОО 1 → сонаправленные

Теорема об углах с сонаправленными сторонами Если стороны двух углов соответственно сонаправлены, то такие углы равны. Дано: угол О и угол О 1 с сонаправленными сторонами. А О Доказать: О 1 В В 1 А 1

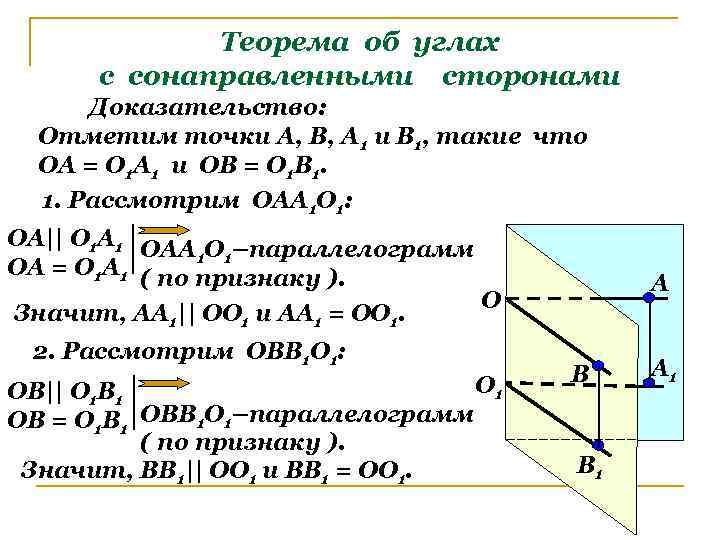
Теорема об углах с сонаправленными сторонами Доказательство: Отметим точки А, В, А 1 и В 1, такие что ОА = О 1 А 1 и ОВ = О 1 В 1. 1. Рассмотрим ОАА 1 О 1: ОА|| О 1 А 1 ОАА О –параллелограмм 1 1 ОА = О 1 А 1 ( по признаку ). О Значит, АА 1|| ОО 1 и АА 1 = ОО 1. 2. Рассмотрим ОВВ 1 О 1: О 1 ОВ|| О 1 В 1 ОВ = О 1 В 1 ОВВ 1 О 1–параллелограмм ( по признаку ). Значит, ВВ 1|| ОО 1 и ВВ 1 = ОО 1. А В В 1 А 1

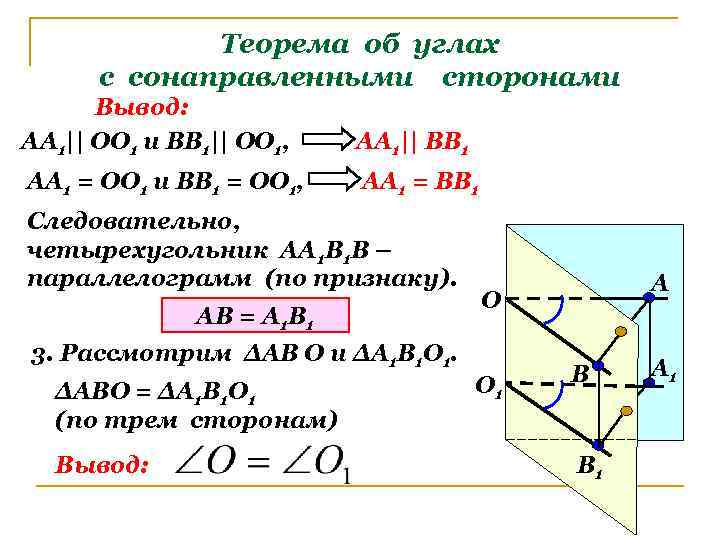
Теорема об углах с сонаправленными сторонами Вывод: АА 1|| ОО 1 и ВВ 1|| ОО 1, АА 1|| ВВ 1 АА 1 = ОО 1 и ВВ 1 = ОО 1, АА 1 = ВВ 1 Следовательно, четырехугольник АА 1 В 1 В – параллелограмм (по признаку). АВ = А 1 В 1 О 3. Рассмотрим ∆АВ О и ∆А 1 В 1 О 1. ∆АВО = ∆А 1 В 1 О 1 (по трем сторонам) Вывод: А О 1 В В 1 А 1

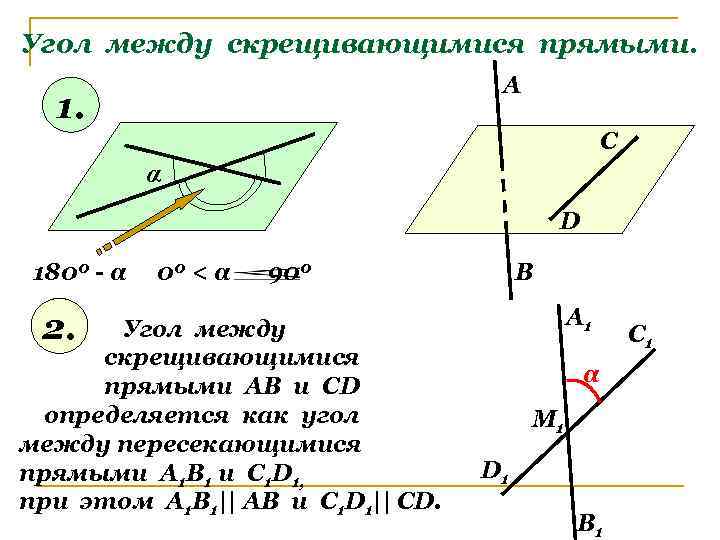
Угол между скрещивающимися прямыми. А 1. С α D 1800 - α 00 < α 900 В А 1 2. Угол между скрещивающимися прямыми АВ и СD определяется как угол между пересекающимися прямыми А 1 В 1 и С 1 D 1, при этом А 1 В 1|| АВ и С 1 D 1|| CD. α М 1 D 1 В 1 С 1

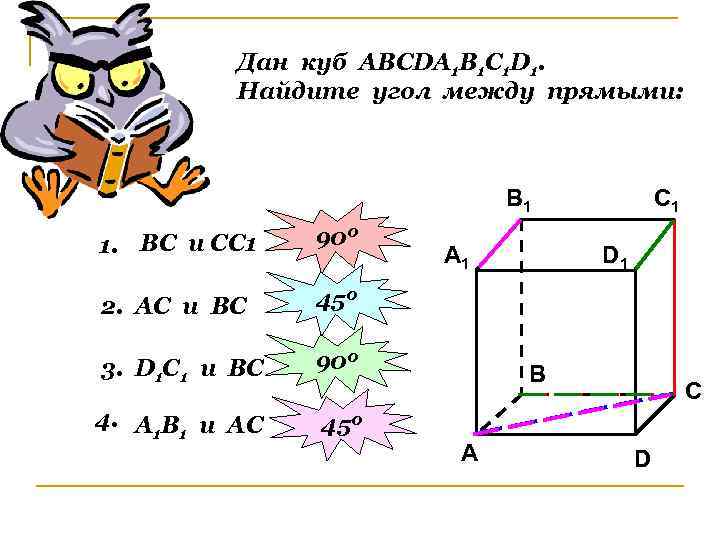
Дан куб АВСDА 1 В 1 С 1 D 1. Найдите угол между прямыми: B 1 1. ВС и СС 1 900 2. АС и ВС 450 3. D 1 С 1 и ВС 900 4. А 1 В 1 и АС C 1 450 A 1 D 1 B A C D

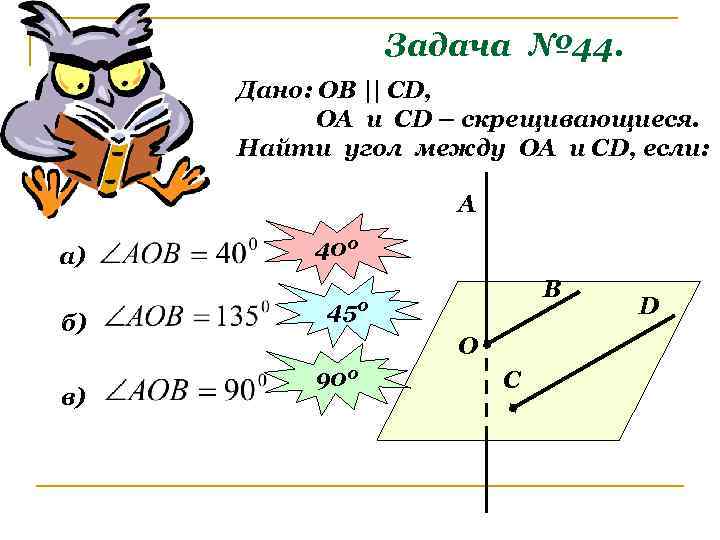
Задача № 44. Дано: ОВ || СD, ОА и СD – скрещивающиеся. Найти угол между ОА и СD, если: A а) б) в) 400 В 450 О 900 C D

Скачать презентацию Угол между прямыми Любая прямая а лежащая

Угол между прямыми.ppt

Количество слайдов: 9