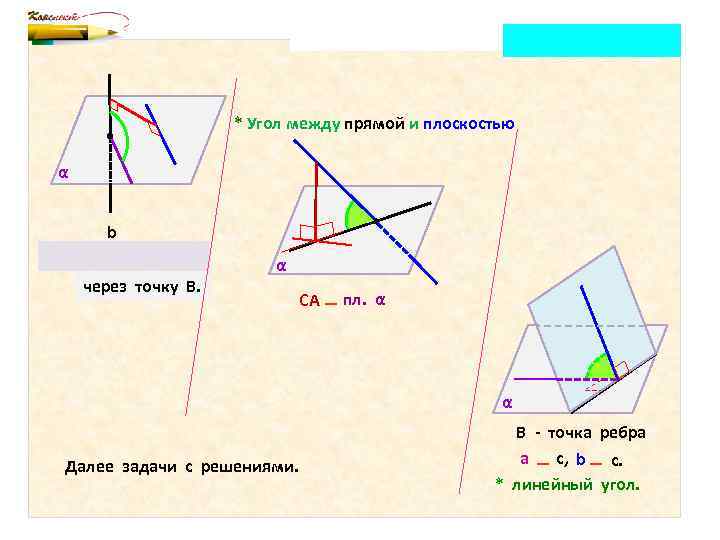
Угол между прямой и плоскостью

• * Угол между прямой и плоскостью α • b через точку В. α СА пл. α α Далее задачи с решениями. В - точка ребра с, b с. а * линейный угол.

, если — • — — в том числе и к • — — —

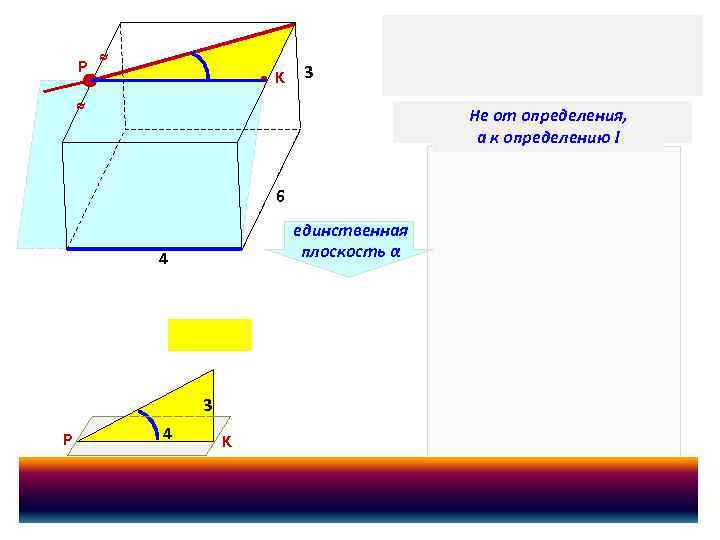P ≈ • • K 3 ≈ Не от определения, а к определению ! скрещивающиеся 6 единственная плоскость α 4 • α 3 P 4 K

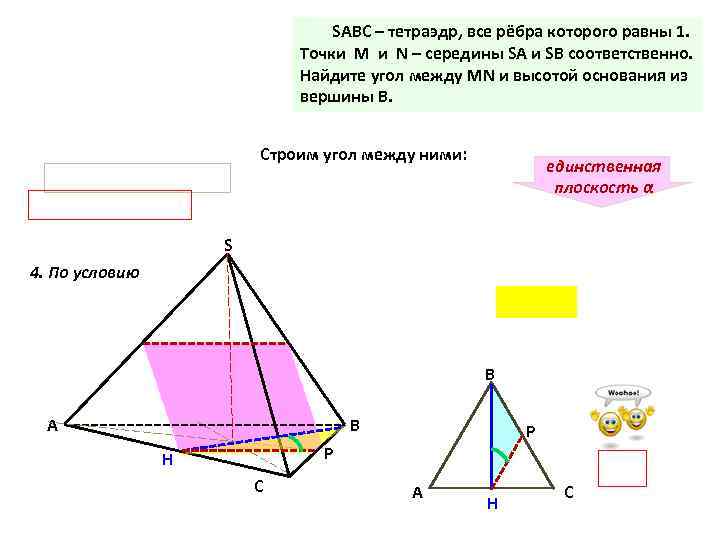SАВС – тетраэдр, все рёбра которого равны 1. Точки M и N – середины SA и SB соответственно. Найдите угол между MN и высотой основания из вершины В. Строим угол между ними: единственная плоскость α S 4. По условию B А B P P H C А H C

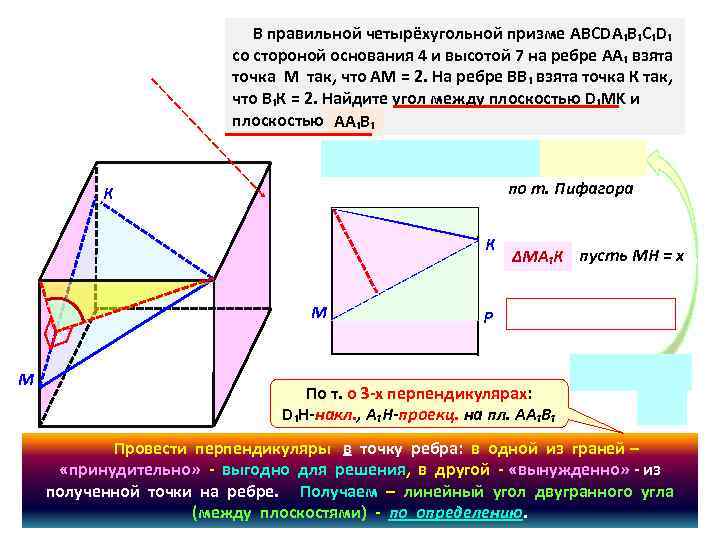В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ со стороной основания 4 и высотой 7 на ребре АА₁ взята точка М так, что АМ = 2. На ребре ВВ₁ взята точка К так, что В₁К = 2. Найдите угол между плоскостью D₁MK и плоскостью CC₁D₁. АА₁В₁ по т. Пифагора К К М М ∆МА₁К пусть МН = х P По т. о 3 -х перпендикулярах: D₁H-накл. , А₁Н-проекц. на пл. АА₁В₁ Провести перпендикуляры в точку ребра: в одной из граней – «принудительно» - выгодно для решения, в другой - «вынужденно» - из полученной точки на ребре. Получаем – линейный угол двугранного угла (между плоскостями) - по определению.

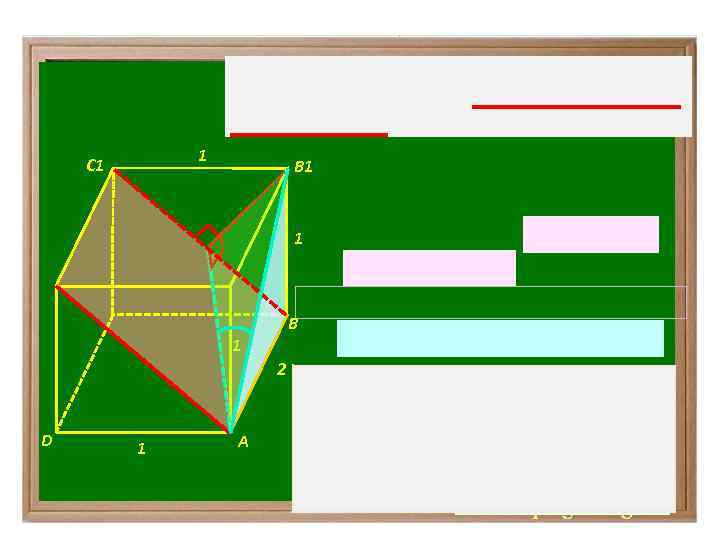1 С 1 В 1 2 D 1 1 С₁ Н А С В₁ В₁ 1 В Н А

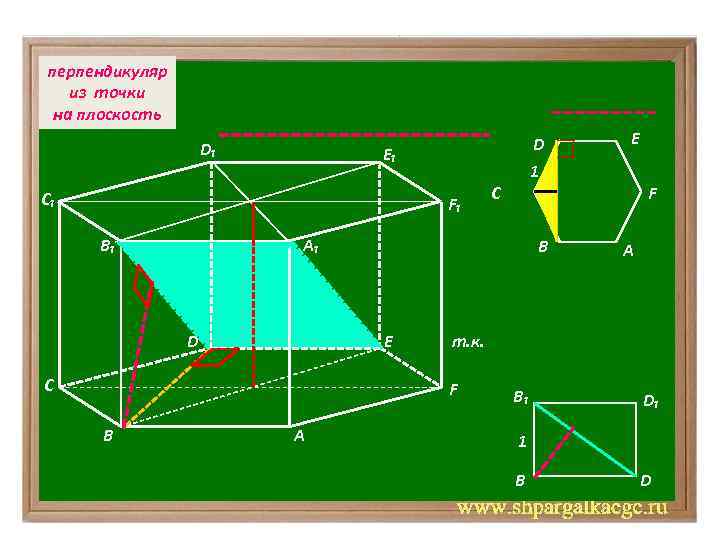перпендикуляр из точки на плоскость D₁ D E₁ C₁ 1 F₁ B₁ B E C A A т. к. F B F C A₁ D E B₁ D₁ 1 B D

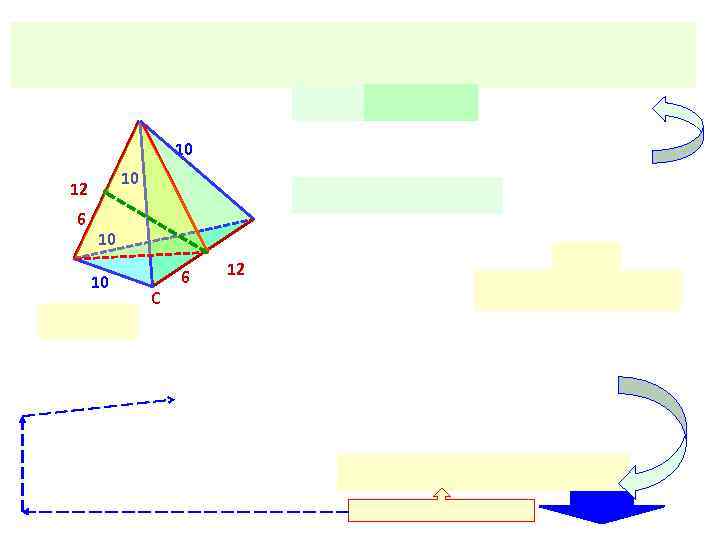10 12 • 6 10 10 10 С 6 12

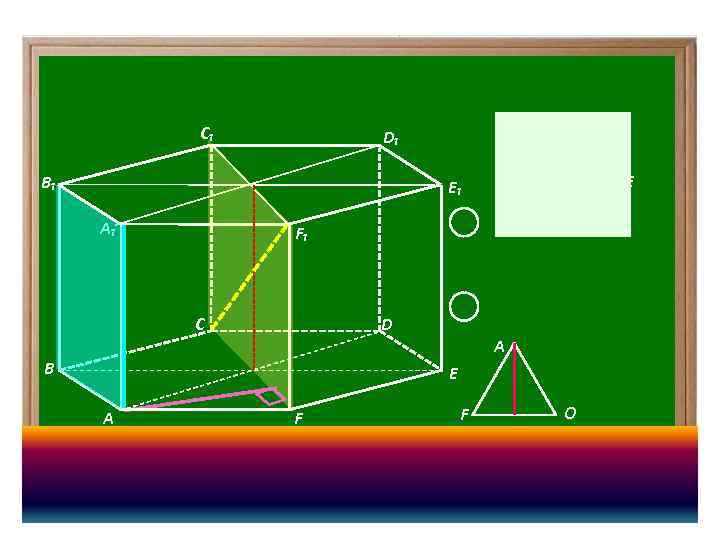C₁ C D₁ B₁ B E₁ A₁ F D A B E A F F E Н A F₁ C D O

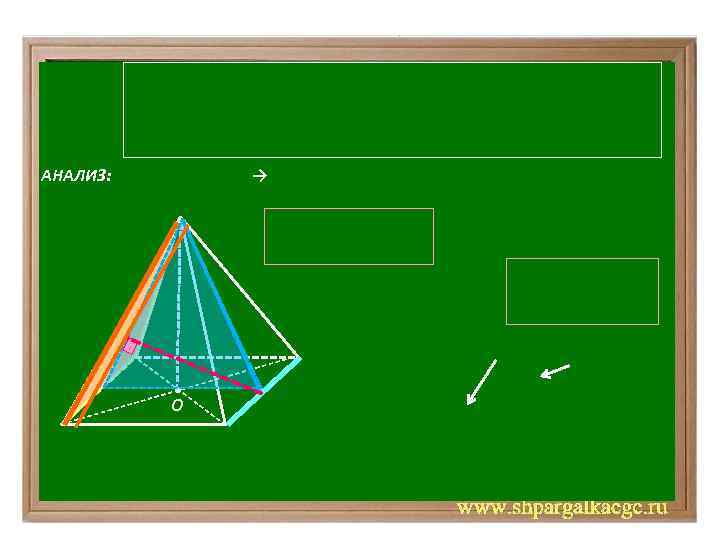АНАЛИЗ: → • O

● ●
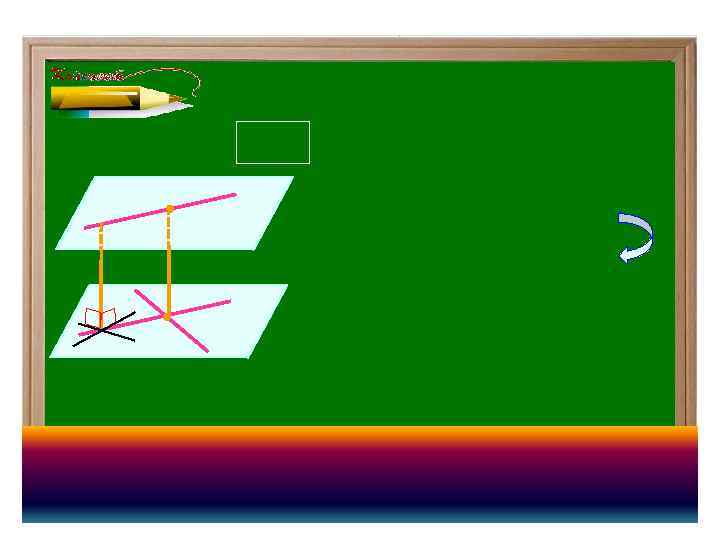