УГЛЫ В ПРОСТРАНСТВЕ А Азевич г Москва

УГЛЫ В ПРОСТРАНСТВЕ А. Азевич, г. Москва

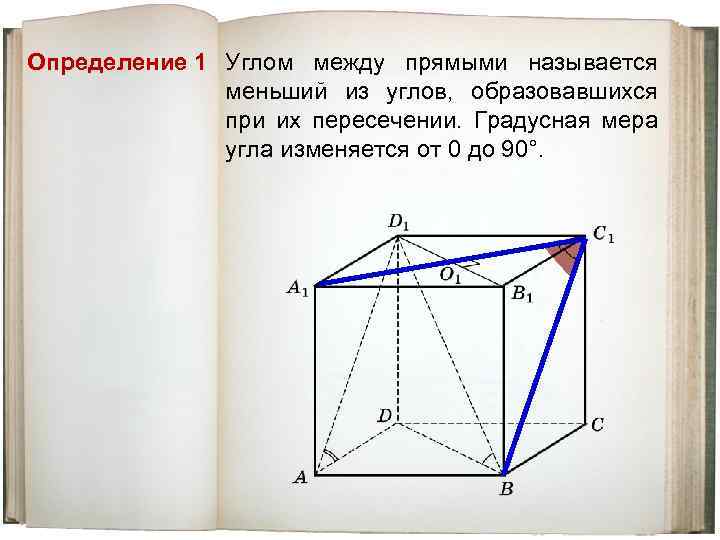Определение 1 Углом между прямыми называется меньший из углов, образовавшихся при их пересечении. Градусная мера угла изменяется от 0 до 90°.

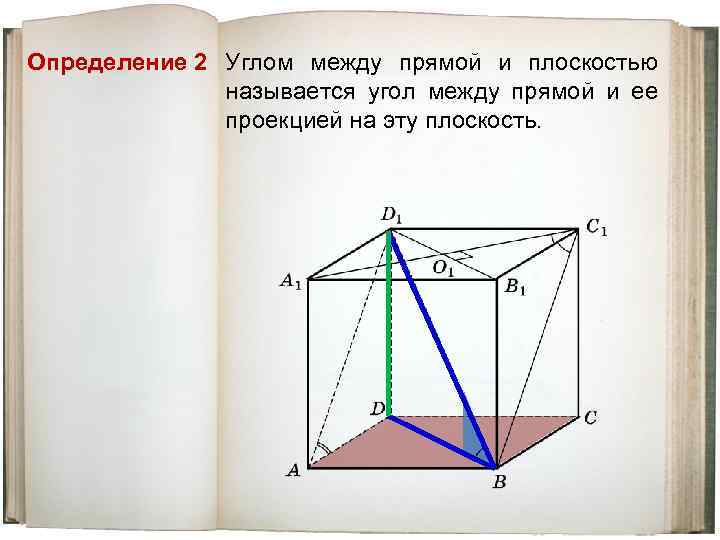Определение 2 Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость.

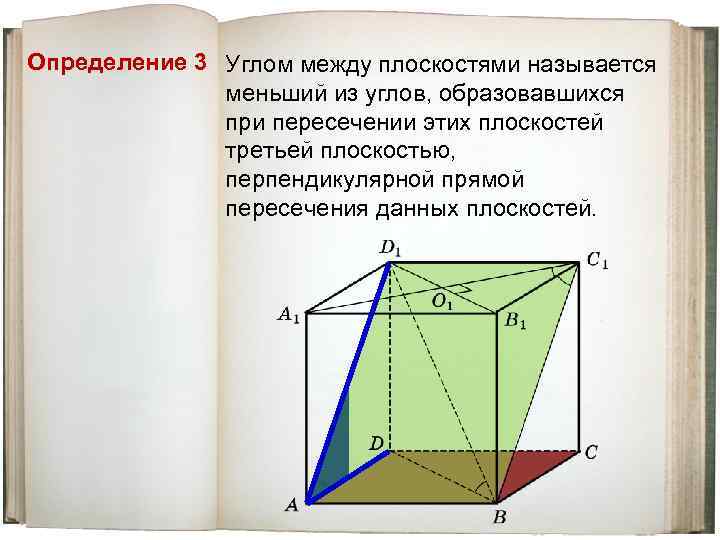Определение 3 Углом между плоскостями называется меньший из углов, образовавшихся при пересечении этих плоскостей третьей плоскостью, перпендикулярной прямой пересечения данных плоскостей.

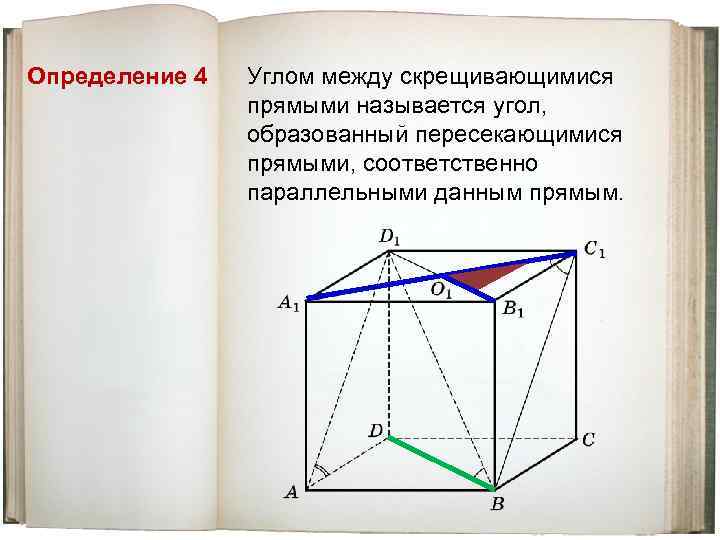Определение 4 Углом между скрещивающимися прямыми называется угол, образованный пересекающимися прямыми, соответственно параллельными данным прямым.

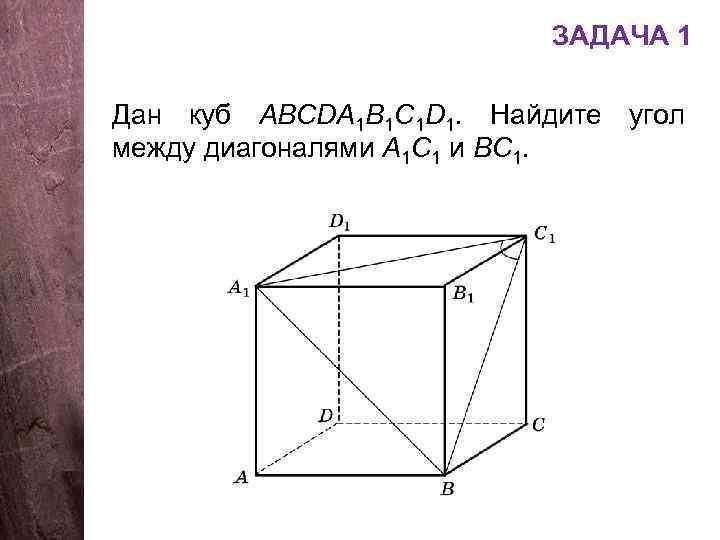ЗАДАЧА 1 Дан куб АВСDA 1 B 1 C 1 D 1. Найдите угол между диагоналями А 1 С 1 и ВС 1.

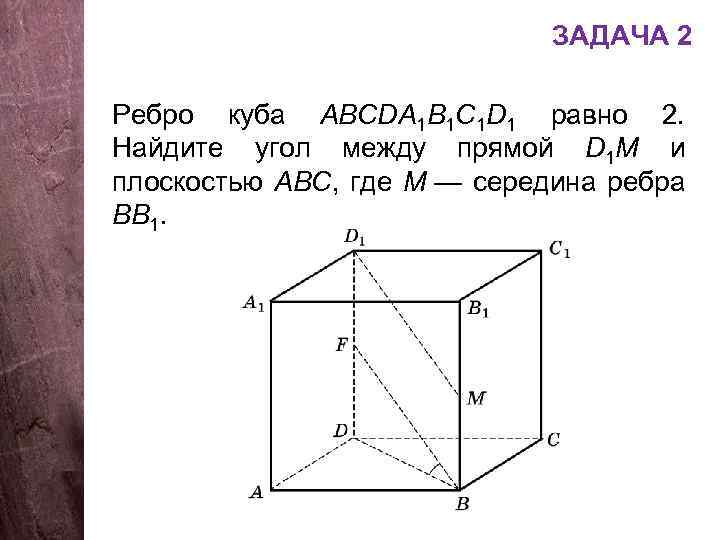ЗАДАЧА 2 Ребро куба АВСDA 1 B 1 C 1 D 1 равно 2. Найдите угол между прямой D 1 M и плоскостью АВС, где М — середина ребра ВВ 1.

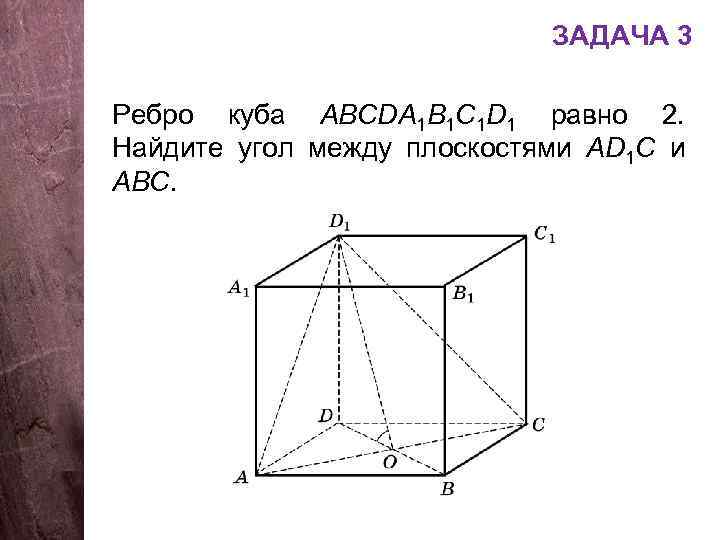ЗАДАЧА 3 Ребро куба АВСDA 1 B 1 C 1 D 1 равно 2. Найдите угол между плоскостями АD 1 C и АВС.

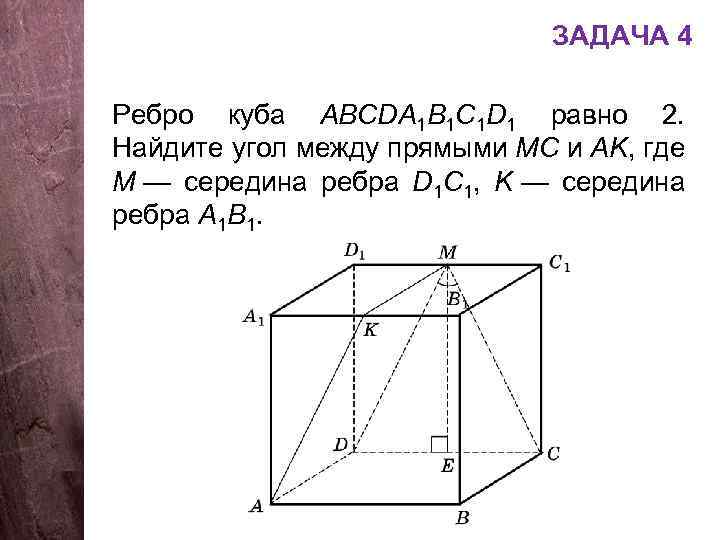ЗАДАЧА 4 Ребро куба АВСDA 1 B 1 C 1 D 1 равно 2. Найдите угол между прямыми МС и АK, где М — середина ребра D 1 C 1, K — середина ребра A 1 B 1.