УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ Гр ивт 12

УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ Гр. ивт 12 д Марченко Павел

Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдельные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R. Ее положение через промежуток времени t зададим углом . Элементарные (бесконечно малые) углы поворота рассматривают как векторы. Мо дуль вектора равен углу поворота, а его направление d совпадает с направле нием поступательного движения острия винта, головка которого вращается в на правлении движения точки по окружности, т. е. подчиняется правилу правого, винта d 0 R r S

Угловой скоростью называется вектор ная величина, равная первой производной угла поворота тела по времени: =lim t 0 = t t

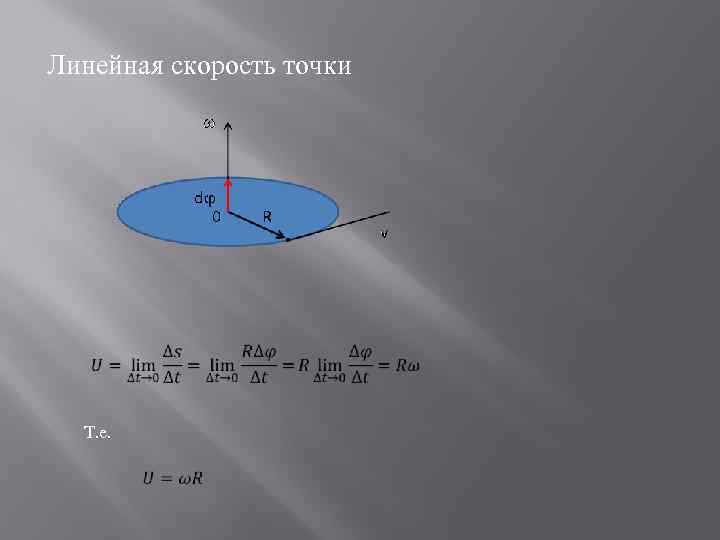Линейная скорость точки Т. е.

Если =const, то вращение равномер ное и его можно характеризовать перио дом вращения. Т — временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2. Так как промежутку времени t=T соответствует =2 , то = 2 /Т, откуда T=2 /

Частота вращения Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени n=1/T= /(2 ) откуда =2 n

Угловое ускорение Векторная величина, равная первой производной угловой скорости по времени:

При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой ско рости. >0 1 2 При ускоренном движении вектор сонаправлен вектору <0 2 1 при замедленном. — противонаправлен ему

Cвязь между линейны ми (длина пути , s пройденного точкой по дуге окружности радиуса R, линейная ско рость , тангенциальное ускорение а , v нор мальное ускорение а) и угловыми величи нами n (угол поворота , угловая скорость (о, угловое ускорение ) выражается сле дующими формулами: s=R v=R а =R 2 Аn= R

В случае равнопеременного движения точки по окружности ( =const) = 0 + t где 0 — начальная угловая скорость. 2 = 0 t + t /2 -

Спасибо за внимание!