99357cbe3fb68f46dd0e45d7939485e6.ppt
- Количество слайдов: 36

Учитель Бунакова Л. А. 2014 г.

Формулы сокращенного умножения Основная цель данной работы – выработать умение применять в несложных случаях формулы сокращенного умножения для преобразования целых выражений в многочлены и для разложения многочленов на множители. Для осознанного применения формул сокращенного умножения раскрыт геометрический смысл некоторых формул, рассказано об истории их возникновения. Как было у древних ? Когда появились буквы ? Зачем нужны формулы сокращенного умножения ? Учись применять формулы сокращенного умножения ? Источники знаний б авторе

При умножении многочлена на многочлен каждый член одного многочлена умножают на каждый член другого. ( a + b )( c + d ) = ac + ad + bc + bd Однако в некоторых случаях умножение многочленов можно выполнить короче, воспользовавшись формулами сокращенного умножения: (a+b)2=a 2+2 ab+b 2 (a-b)2=a 2 -2 ab+b 2 a 2 -b 2=(a+b)(a-b) a 3+b 3=(a+b)(a 2 -ab+b 2) a 3 -b 3=(a-b)(a 2+ab+b 2)

Геометрическая алгебра в древности Найденные древневавилонские клинописные тексты свидетельствуют, что некоторые формулы умножения ( квадрат суммы, квадрат разности, произведение суммы на разность ) были известны еще около 4000 лет назад. Их знали не в нашем символическом виде, а словесно, или в геометрической форме, как у древних греков. Ученые Древней Греции представляли величины отрезками прямых: Символиче Геометрический язык ская запись ab Фигура Прямоугольник, содержащийся между отрезками a и b b a a 2 Квадрат на отрезке a a

Появление буквенной символики. Диофант У Диофанта (III в) неизвестное, названное «аритмос» , обозначалось знаком . Особые обозначения имели степени. Значительно превзошли Диофанта в деле применения сокращенных записей древние индийцы. Европейские математики XVI – XVII в. вторую степень неизвестного называли «сила» (по-латыни (Census), а также «квадрат» (Quadratus), третью степень «куб» (Cubus). Виет применял сокращения: N (Numerus, число) для первой степени, Q – для второй, C – для третьей, QQ – для четвертой степени и т. д. Например: 1 C – 8 Q =16 N aequatur 40 означает в современной записи : x 3 – 8 x 2 + 16 x = 40. A 3 , Тартальи Декарт a 4. М. Штифель писал AAA вместо Т. Гарриот писал aaaa вместо 3 + 5 x 2 – 4 x +6 записывал так: 3(3) + 5(2) – 4(1) + 6. С. Стевин выражение 3 x Современная запись была введена Декартом и систематически применялась им в его «Геометрии» . Штифель Стевин Круглые скобки появляются в XV в. в трудах Штифеля, Тартальи и др. В конце того же века появляются и фигурные скобки в книгах Виета. Однако в течение почти всего XVII в. Употреблялись не скобки, а горизонтальная черта, проводимая над выражением, подлежащим включению в скобки. Широкое применение скобки получили в первой половине XVIII в. благодаря Лейбницу и Эйлеру. Лейбниц Эйлер

Подробнее узнать о формулах сокращенного умножения можно в книгах и интернет - сайтах: a Алгебра: Учеб. Для 7 кл. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского. – М. : Просвещение. a Мордкович А. Г. Алгебра. Учеб для 7 кл. –М. : Мнемозина. a Пичурин Л. В. За страницами учебника алгебры: Кн. Для учащихся 7 – 9 кл. – М. : Просвещение, 1990. a Глейзер Г. И. история математики в школе: IV – VI кл. Пособие для учителей. – М. : Просвещение, 1981 a Сайт школы N 43: ЭКСПЕРИМЕНТ - Мастер-класс Математика http: //www. infovolga. ru/school_2002/school_43/page 232. htm a Untitled Электронный учебник "Формулы сокращенного умножения" a Электронные учебники. Математика a Геометрические иллюстрации в элементарной алгебре | Хранилище методических. . . http: //method. samara. rcde. ru/item. asp? id=600000136 a Неофициальный сайт Борисовского Государственного Политехнического Колледжа. . . Программа считает за тебя по формулам сокращённого умножения http: //co 11 ege. narod. ru/indexsoft. html (19 КБ)
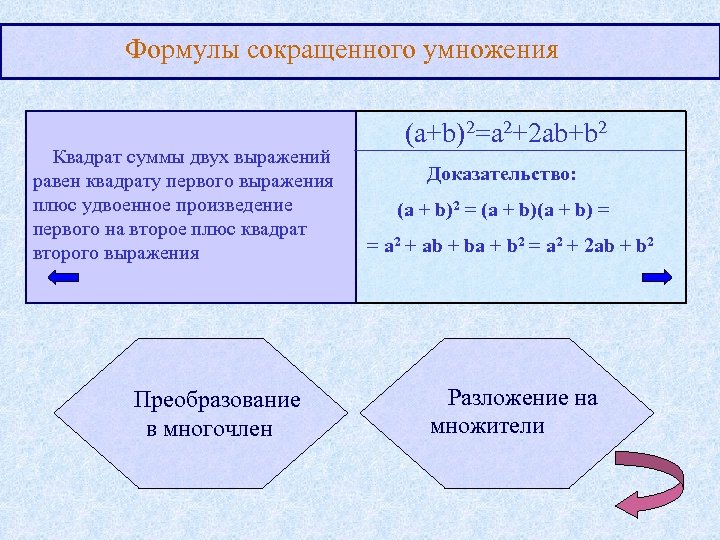
Формулы сокращенного умножения Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого на второе плюс квадрат второго выражения Преобразование в многочлен (a+b)2=a 2+2 ab+b 2 Доказательство: (a + b)2 = (a + b) = = a 2 + ab + ba + b 2 = a 2 + 2 ab + b 2 Разложение на множители

Формулы сокращенного умножения Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого на второе плюс квадрат второго выражения Преобразование в многочлен (a-b)2=a 2 -2 ab+b 2 Доказательство: (a - b)2 = (a - b) = = a 2 - ab - ba + b 2 = a 2 - 2 ab + b 2 Разложение на множители
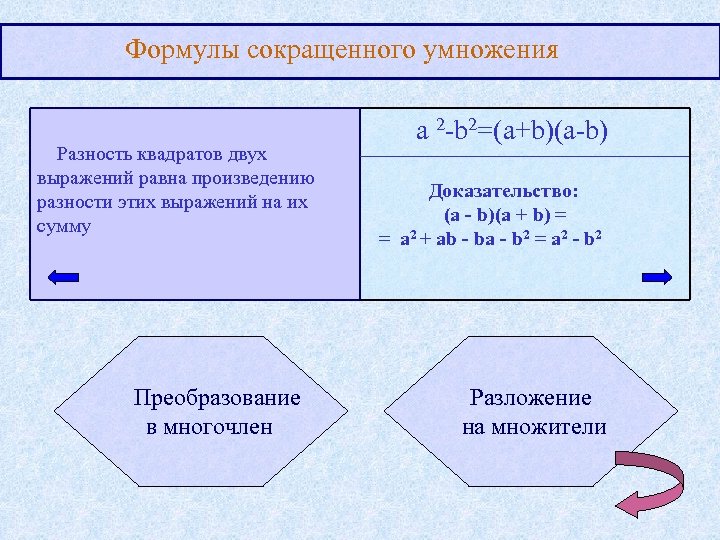
Формулы сокращенного умножения Разность квадратов двух выражений равна произведению разности этих выражений на их сумму Преобразование в многочлен a 2 -b 2=(a+b)(a-b) Доказательство: (a - b)(a + b) = = a 2 + ab - ba - b 2 = a 2 - b 2 Разложение на множители

Формулы сокращенного умножения Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат разности этих выражений a 3+b 3=(a+b)(a 2 -ab+b 2) Доказательство: (a + b)(a 2 – ab + b 2) = = a 3 – a 2 b + ab 2 + ba 2 – ab 2 + b 3 = = a 3 + b 3 Разложение на множители

Формулы сокращенного умножения Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат суммы этих выражений a 3 -b 3=(a-b)(a 2+ab+b 2) Доказательство: (a - b)(a 2 + ab + b 2) = = a 3 + a 2 b + ab 2 - ba 2 – ab 2 - b 3 = = a 3 + b 3 Разложение на множители

(a+b)2=a 2+2 ab+b 2 a – первое ( I ) выражение, b – второе (II) выражение ( I + II )2 = I 2+2·I·II+II 2 Пример: ( 6 q + c )2 = (6 q)2 + 2 (6 q) c + c 2 = 36 q 2 + 12 qc + c 2 Реши сам Представь в виде многочлена: а) (6 h + 9 m)2 б) (10 + 8 k)2 в) (12 c 2 + a 6 c)2 Проверь себя

(a+b)2=a 2+2 ab+b 2 a – первое ( I ) выражение, b – второе (II) выражение ( I + II )2 = I 2+2·I·II+II 2 Пример: ( 6 q + c )2 = (6 q)2 + 2 (6 q) c + c 2 = 36 q 2 + 12 qc + c 2 Реши сам Представь в виде многочлена: а) (6 h + 9 m)2 б) (10 + 8 k)2 в) (12 c 2 + a 6 c)2 Проверь себя = 36 h 2 + 108 hm + 81 m 2 = 100 + 160 k + 64 k 2 = 144 c 4 + 24 a 6 c 3 + a 12 c 2

a 2+2 ab+b 2= (a+b)2 a – первое ( I ) выражение, b – второе ( II) выражение I 2+2·I·II+II 2= ( I + II )2 Пример: 4 x 2 + 12 x + 9 = (2 x)2 + 2· 2 x· 3 + 32 = (2 x + 3)2 Реши сам Представьте в виде квадрата двучлена: а) 16 a 2 +8 ab +b 2 б) 9 y 2 + c 2 d 2 + 6 cdy в) 0, 25 a 2 + 2 ab 2 + 4 b 4 Проверь себя

a 2+2 ab+b 2= (a+b)2 a – первое ( I ) выражение, b – второе ( II) выражение I 2+2·I·II+II 2= ( I + II )2 Пример: 4 x 2 + 12 x + 9 = (2 x)2 + 2· 2 x· 3 + 32 = (2 x + 3)2 Реши сам Представьте в виде квадрата двучлена: а) 16 a 2 +8 ab +b 2 б) 9 y 2 + c 2 d 2 + 6 cdy в) 0, 25 a 2 + 2 ab 2 + 4 b 4 Проверь себя = (4 a + b)2 = (3 y + cd)2 = (0, 5 a + 2 b)2

(a-b)2=a 2 -2 ab+b 2 a – первое ( I ) выражение, b – второе ( II) выражение ( I - II )2 = I 2 -2·I·II+II 2 Пример: (x 3 – 3 y 4)2 = (x 3)2 - 2·(x 3)(3 y 4) + (3 y 4)2 = x 6 – 6 x 3 y 4 + 9 y 8 Реши сам Представь в виде многочлена: а) (q 3 – 4 p)2 б) (3 a – 2 b)2 в) (c 2 – 0, 7 c 3)2 Проверь себя

(a-b)2=a 2 -2 ab+b 2 a – первое ( I ) выражение, b – второе ( II) выражение ( I - II )2 = I 2 -2·I·II+II 2 Пример: (x 3 – 3 y 4)2 = (x 3)2 - 2·(x 3)(3 y 4) + (3 y 4)2 = x 6 – 6 x 3 y 4 + 9 y 8 Реши сам Представь в виде многочлена: а) (q 3 – 4 p)2 б) (3 a – 2 b)2 в) (c 2 – 0, 7 c 3)2 Проверь себя = q 6 – 8 q 3 p + 16 p 2 = 9 a 2 – 12 ab + 4 b 2 = c 4 – 1, 4 c 5 + 0, 49 c 6

a 2 -2 ab+b 2 = (a – b)2 a – первое ( I ) выражение, b – второе ( II) выражение I 2 - 2· I ·II + II 2 = ( I - II )2 Пример: a 2 x 2 – 2 abx + b 2 = (ax)2 – 2(ax)b + b 2 = (ax – b)2 Реши сам Представь в виде квадрата двучлена: а) 9 a 2 – 42 a +49 б) 25 b 2 – 10 b + 1 в) 4 a 6 – 4 a 3 b 2 + b 4 Проверь себя

a 2 -2 ab+b 2 = (a – b)2 a – первое ( I ) выражение, b – второе ( II) выражение I 2 - 2· I ·II + II 2 = ( I - II )2 Пример: a 2 x 2 – 2 abx + b 2 = (ax)2 – 2(ax)b + b 2 = (ax – b)2 Реши сам Представь в виде квадрата двучлена: а) 9 a 2 – 42 a +49 б) 25 b 2 – 10 b + 1 в) 4 a 6 – 4 a 3 b 2 + b 4 Проверь себя = (3 a – 7)2 = (5 b – 1)2 = (2 a 3 – b 2)2
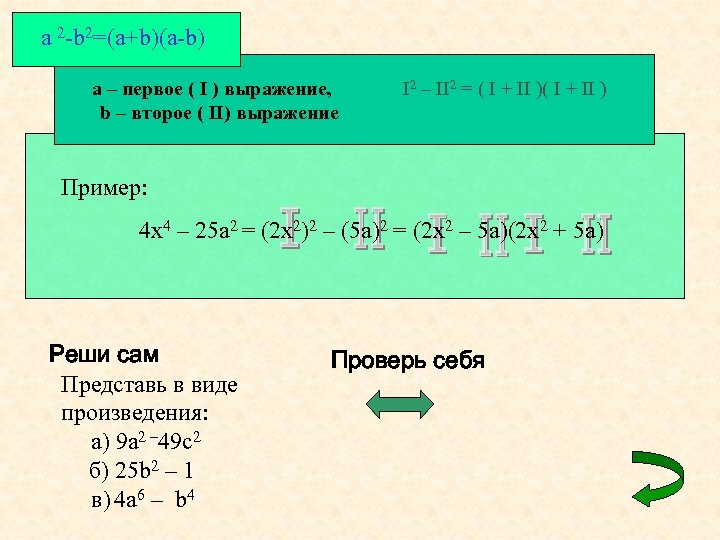
a 2 -b 2=(a+b)(a-b) a – первое ( I ) выражение, b – второе ( II) выражение I 2 – II 2 = ( I + II ) Пример: 4 x 4 – 25 a 2 = (2 x 2)2 – (5 a)2 = (2 x 2 – 5 a)(2 x 2 + 5 a) Реши сам Представь в виде произведения: а) 9 a 2 – 49 с2 б) 25 b 2 – 1 в) 4 a 6 – b 4 Проверь себя

a 2 -b 2=(a+b)(a-b) a – первое ( I ) выражение, b – второе ( II) выражение I 2 – II 2 = ( I + II ) Пример: 4 x 4 – 25 a 2 = (2 x 2)2 – (5 a)2 = (2 x 2 – 5 a)(2 x 2 + 5 a) Реши сам Представь в виде произведения: а) 9 a 2 – 49 с2 б) 25 b 2 – 1 в) 4 a 6 – b 4 Проверь себя = (3 a – 7 c)(3 a + 7 c) = (5 b – 1)(5 b + 1) = (2 a 3 – b 2)(2 a 3 + b 2)

(a+b)(a-b) = a 2 -b 2 a – первое ( I ) выражение, b – второе ( II) выражение ( I + II ) = I 2 – II 2 Пример: (6 x – a)(6 x + a) = (6 x)2 – a 2 = 36 x 2 – a 2 Реши сам Выполните умножение: а) (6 h – 9 m)(6 h + 9 m) б) (10 – 8 k)(10 + 8 k) в) (12 c 2 - a 6 c) (12 c 2 + a 6 c) Проверь себя

(a+b)(a-b) = a 2 -b 2 a – первое ( I ) выражение, b – второе ( II) выражение ( I + II ) = I 2 – II 2 Пример: (6 x – a)(6 x + a) = (6 x)2 – a 2 = 36 x 2 – a 2 Реши сам Проверь себя Выполните умножение: = 36 h 2 - 81 m 2 а) (6 h – 9 m)(6 h + 9 m) = 100 - 64 k 2 б) (10 – 8 k)(10 + 8 k) в) (12 c 2 - a 6 c) (12 c 2 + a 6 c) = 144 c 4 - a 12 c 2
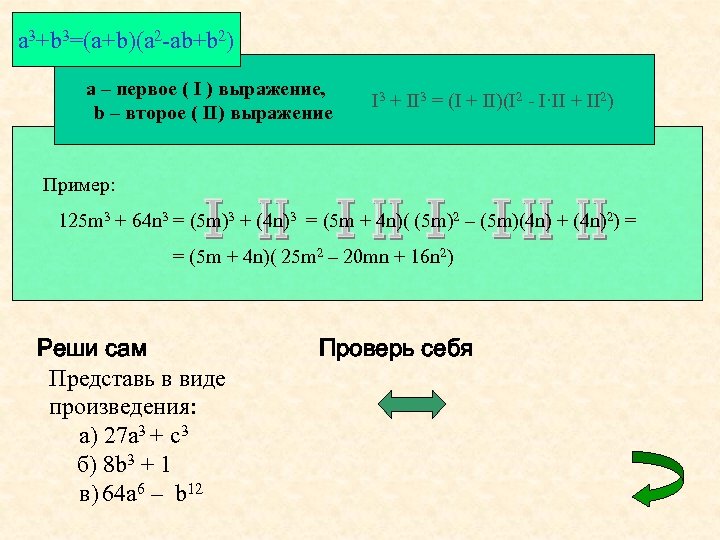
a 3+b 3=(a+b)(a 2 -ab+b 2) a – первое ( I ) выражение, b – второе ( II) выражение I 3 + II 3 = (I + II)(I 2 - I·II + II 2) Пример: 125 m 3 + 64 n 3 = (5 m)3 + (4 n)3 = (5 m + 4 n)( (5 m)2 – (5 m)(4 n) + (4 n)2) = = (5 m + 4 n)( 25 m 2 – 20 mn + 16 n 2) Реши сам Представь в виде произведения: а) 27 a 3 + с3 б) 8 b 3 + 1 в) 64 a 6 – b 12 Проверь себя

a 3+b 3=(a+b)(a 2 -ab+b 2) a – первое ( I ) выражение, b – второе ( II) выражение I 3 + II 3 = (I + II)(I 2 - I·II + II 2) Пример: 125 m 3 + 64 n 3 = (5 m)3 + (4 n)3 = (5 m + 4 n)( (5 m)2 – (5 m)(4 n) + (4 n)2) = = (5 m + 4 n)( 25 m 2 – 20 mn + 16 n 2) Реши сам Представь в виде произведения: а) 27 a 3 + с3 б) 8 b 3 + 1 в) 64 a 6 + b 12 Проверь себя = (3 a + c)(9 a 2 – 3 ac + c 2) = (2 b + 1)(4 k 2 – 2 b + 1) = (4 c 2 + b 4)(16 c 4 – 4 c 2 b 4 + b 8)

a 3 -b 3=(a-b)(a 2+ab+b 2) a – первое ( I ) выражение, b – второе ( II) выражение I 3 - II 3 = (I - II)(I 2 + I·II + II 2) Пример: 8 - a 3 b 3 = 23 - (ab)3 = (2 - ab)( 22 + 2·ab + (ab)2) = (2 - ab)( 4 + 2 ab +a 2 b 2) Реши сам Представь в виде произведения: а) 1000 q 3 – 216 с2 б) b 3 – 1 в) x 6 y 3 – 27 Проверь себя

a 3 -b 3=(a-b)(a 2+ab+b 2) a – первое ( I ) выражение, b – второе ( II) выражение I 3 - II 3 = (I - II)(I 2 + I·II + II 2) Пример: 8 - a 3 b 3 = 23 - (ab)3 = (2 - ab)( 22 + 2·ab + (ab)2) = (2 - ab)( 4 + 2 ab +a 2 b 2) Реши сам Проверь себя Представь в виде произведения: а) 1000 q 3 – 216 p 3 = (10 q – 6 p)(100 q 2 + 60 qp+ 36 p 2) б) b 3 – 1 = (b – 1)(b 2 + b + 1) в) x 6 y 3 – 27 = (x 3 y – 3)(x 4 y 2 + 3 x 3 y + 9)

Геометрический смысл формулы (a+b)2=a 2+2 ab+b 2 раскрывает предложение 4 (теорема) книги второй «Начал» Евклида. Формулировка Евклида Геометрическая иллюстрация Если отрезок как-либо разбит на два отрезка, то площадь квадрата, построенного на всем отрезке равна сумме площадей квадратов, построенных на каждом из этих отрезков и удвоенной площади прямоугольника , сторонами которого служат эти отрезки. Повторить анимацию b ab b 2 Символическая запись a, b S = (a + b)2 a a 2 ba a S 1 = a 2 , S 2 = b 2 b S = S 1 + S 3 + S 4 + S 2 или (a+b)2=a 2+2 ab+b 2 S 3 = ab, S 4 = ba

Геометрический смысл формулы (a+b)2=a 2+2 ab+b 2 раскрывает предложение 4 (теорема) книги второй «Начал» Евклида. Формулировка Евклида Геометрическая иллюстрация Если отрезок как-либо разбит на два отрезка, то площадь квадрата, построенного на всем отрезке равна сумме площадей квадратов, построенных на каждом из этих отрезков и удвоенной площади прямоугольника , сторонами которого служат эти отрезки. Повторить анимацию b ab b 2 Символическая запись a, b S = (a + b)2 a a 2 ba a S 1 = a 2 , S 2 = b 2 b S = S 1 + S 3 + S 4 + S 2 или (a+b)2=a 2+2 ab+b 2 S 3 = ab, S 4 = ba

Геометрический смысл формулы (a+b)2=a 2+2 ab+b 2 раскрывает предложение 4 (теорема) книги второй «Начал» Евклида. Формулировка Евклида Если отрезок как-либо разбит на два отрезка, то площадь квадрата, построенного на всем отрезке равна сумме площадей квадратов, построенных на каждом из этих отрезков и удвоенной площади прямоугольника , сторонами которого служат эти отрезки. Геометрическая иллюстрация b ab b 2 Символическая запись a, b S = (a + b)2 a a 2 ba a S 1 = a 2 , S 2 = b 2 b S = S 1 + S 3 + S 4 + S 2 или (a+b)2=a 2+2 ab+b 2 S 3 = ab, S 4 = ba

Геометрический смысл формулы (a-b)2=a 2 -2 ab+b 2 для положительных a и b, удовлетворяющих условию a>b раскрывает следующий чертеж: Символическая запись Геометрическая иллюстрация a, b b S 1 = a 2 , S 2 = b 2 S 3 = ab, S 4 = ba S 5 = S 1 + S 2 - S 3 S = S 5 – S 4 S = S 1 + S 2 - S 3 – S 4 или (a-b)2=a 2 -2 ab+b 2 Повторить анимацию ab b 2 a (a-b)2 2 aab a ab b

Геометрический смысл формулы (a-b)2=a 2 -2 ab+b 2 для положительных a и b, удовлетворяющих условию a>b раскрывает следующий чертеж: Символическая запись Геометрическая иллюстрация a, b b S 1 = a 2 , S 2 = b 2 S 3 = ab, S 4 = ba S 5 = S 1 + S 2 - S 3 S = S 5 – S 4 S = S 1 + S 2 - S 3 – S 4 или (a-b)2=a 2 -2 ab+b 2 Повторить анимацию ab b 2 a (a-b)2 2 aab a ab b

Геометрический смысл формулы (a-b)2=a 2 -2 ab+b 2 для положительных a и b, удовлетворяющих условию a>b раскрывает следующий чертеж: Символическая запись Геометрическая иллюстрация a, b b S 1 = a 2 , S 2 = b 2 S 3 = ab, S 4 = ba S 5 = S 1 + S 2 - S 3 S = S 5 – S 4 S = S 1 + S 2 - S 3 – S 4 или (a-b)2=a 2 -2 ab+b 2 ab b 2 a (a-b)2 2 aab a ab b
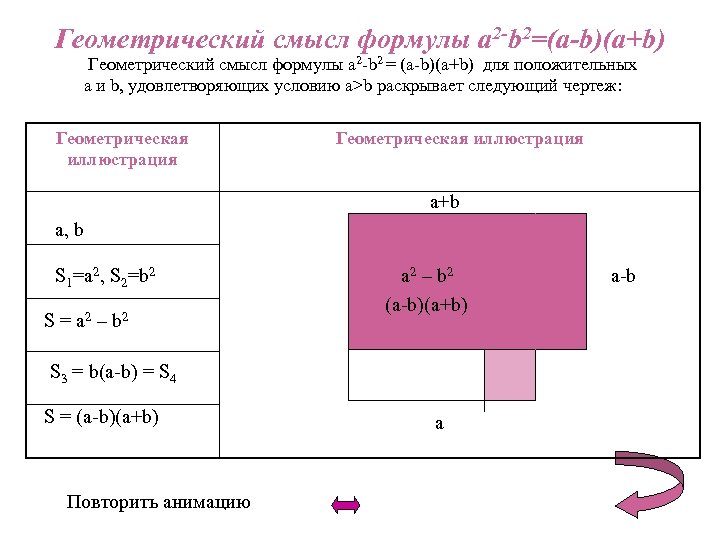
Геометрический смысл формулы a 2 -b 2=(a-b)(a+b) Геометрический смысл формулы a 2 -b 2 = (a-b)(a+b) для положительных a и b, удовлетворяющих условию a>b раскрывает следующий чертеж: Геометрическая иллюстрация a+b a, b S 1=a 2, S 2=b 2 S = a 2 – b 2 S 3 = b(a-b) = S 4 S = (a-b)(a+b) Повторить анимацию a 2 – b 2 (a-b)(a+b) b(a-b) a-b b a
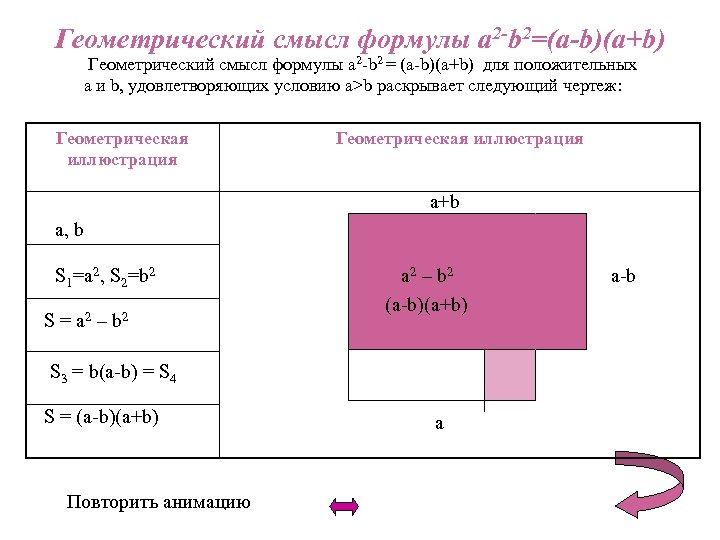
Геометрический смысл формулы a 2 -b 2=(a-b)(a+b) Геометрический смысл формулы a 2 -b 2 = (a-b)(a+b) для положительных a и b, удовлетворяющих условию a>b раскрывает следующий чертеж: Геометрическая иллюстрация a+b a, b S 1=a 2, S 2=b 2 S = a 2 – b 2 S 3 = b(a-b) = S 4 S = (a-b)(a+b) Повторить анимацию a 2 – b 2 (a-b)(a+b) b(a-b) a-b b a
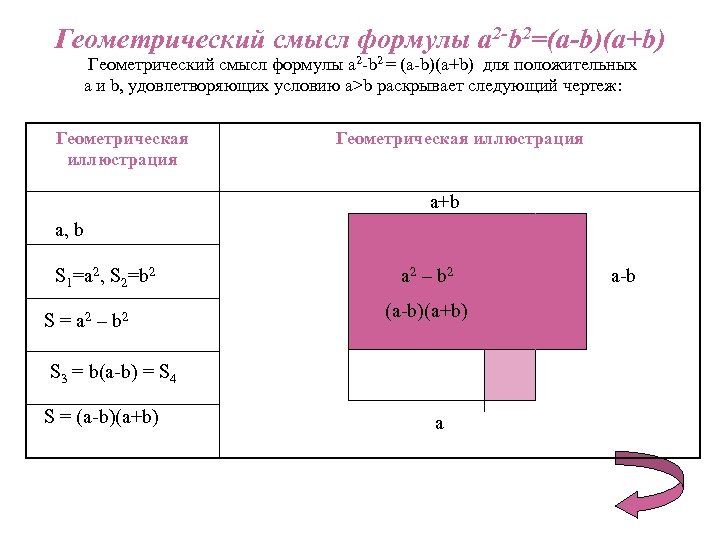
Геометрический смысл формулы a 2 -b 2=(a-b)(a+b) Геометрический смысл формулы a 2 -b 2 = (a-b)(a+b) для положительных a и b, удовлетворяющих условию a>b раскрывает следующий чертеж: Геометрическая иллюстрация a+b a, b S 1=a 2, S 2=b 2 S = a 2 – b 2 S 3 = b(a-b) = S 4 S = (a-b)(a+b) a 2 – b 2 a-b (a-b)(a+b) b(a-b) b a
99357cbe3fb68f46dd0e45d7939485e6.ppt