МОДУЛЬ 1 механика мат точки 2009.ppt
- Количество слайдов: 54

УЧЕБНЫЙ МОДУЛЬ № 1 «МЕХАНИКА МАТЕРИАЛЬНОЙ ТОЧКИ» Кинематика материальной точки • системы координат • кинематические характеристики • средняя и мгновенная скорости • среднее и мгновенное ускорения • движение по окружности Динамика поступательного движения • законы Ньютона • силы в природе • центр масс системы • работа и энергия • поле сил • взаимодействие материальных точек • неинерциальные системы отсчета Элементы специальной теории относительности • Принцип относительности Галилея и постулаты Эйнштейна • Преобразования Лоренца и следствия из них • Основные соотношения релятивистской механики

Механика и ее структура • классическая механика • релятивистская механика • квантовая механика • • • Кинематика — это раздел механики, в котором изучаются геометрические свойства движения тел без учета их массы и действующих сил. • • Динамика изучает движение тел в связи с вызывающими его причинами — взаимодействиями тел. • Статика — изучает законы равновесия системы тел. • Физические модели: Материальная точка — тело, форма и размеры которого несущественны в условиях данной задачи. Абсолютно твердое тело — деформацией которого в условиях данной задачи можно пренебречь и расстояние между любыми двумя точками этого тела остается постоянным. Абсолютно упругое тело — деформация которого подчиняется закону Гука, а после прекращения внешнего силового воздействия такое тело полностью восстанавливает свои первоначальные размеры форму. Абсолютно неупругое тело — полностью сохраняющее деформированное состояние после прекращения действия внешних сил.

ВИДЫ ДВИЖЕНИЯ Механическим движением называется изменение положения тела в пространстве с течением времени. Различают пять видов движения твердого тела: 1) поступательное движение. При поступательном движении любая прямая, Поступательное движение остается параллельной котором жестко связанная с движущимся телом, — это движение, при своему начальному любая положению. прямая жестко связанная с телом, остается параллельной своему первоначальном положению. 2) вращение вокруг неподвижной оси. Вращением вокруг неподвижной оси Вращательное движение — это по крайней при котором называется движение, при котором существуют движение, мере две неподвижные точкивсе точки тела движутся по окружностям, центры которых тела лежат на одной и той же прямой называемой осью вращения. 3) плоское движение. При плоском движении траектория каждой точки твердого тела расположена в некоторой фиксированной плоскости и плоскости движения всех точек параллельны между собой (иначе говоря, все точки тела движутся в параллельных плоскостях). Любое движение твердого тела можно точки называют представить как комбинациюодна точка тела, движение твердого тела, если существует только скорость которой в любой момент времени равна нулю скорость. Движение поступательного и точку, представляет собой твердого тела, имеющего одну неподвижнуювращательного вращение вокруг проходящей через эту точку мгновенной оси (мгновенное вращение). движений. 4) вращение вокруг неподвижной точки. Вращением вокруг неподвижной 5) свободное движение. При свободном движении никаких кинематических ограничений на движение твердого тела не накладывается.

Постулаты классической механики линейные масштабы и промежутки времени остаются неизменными при переходе от одной системы отсчета к другой, они не зависят от выбора системы отсчета время абсолютно пространство абсолютно Способы описания в механике • Векторный способ описания движения • Координатный способ описания движения • Естественно-параметрический способ описания движения частицы описания

СИСТЕМА КООРДИНАТ • Тело отсчета — произвольно выбранное тело, относительно которого определяется положение остальных тел. • Система отсчета — совокупность системы координат и часов, связанных с телом отсчета. • Декартова прямоугольная система координат — это три пересекающиеся в одной точке (начало координат) взаимно перпендикулярные оси х, у, z • радиус-вектор • Эти уравнения называются кинематическими уравнениями движения точки.

СИСТЕМА КООРДИНАТ • Декартова прямоугольная система координат — это три пересекающиеся в одной точке (начало координат) взаимно перпендикулярные оси х, у, z • Положение тела на плоскости удобно определять в полярной системе координат • В сферической системе координат положение тела в пространстве задается тремя числами

Векторный способ описания движения Положение частицы в пространстве в любой момент времени задается радиус-вектором Траектория — это линия в пространстве, вдоль которой движется частица (геометрическое место концов радиуса вектора частицы). Длиной пути точки называется сумма длин всех участков траектории, пройденных этой точкой за рассматриваемый промежуток времен Перемещение — вектор, проведенный из начального в конечное положение частицы Скорость — это векторная величина, которая определяет как быстроту движения, так и его направление в данный момент времени. Вектором средней скорости за интервал времени t называется отношение приращения r радиуса вектора точки к промежутку времени t

СКОРОСТЬ Скорость — это векторная величина, которая определяет как быстроту движения, так и его направление в данный момент времени. Вектором средней скорости за интервал времени t называется отношение приращения r радиуса вектора точки к промежутку времени t Мгновенная скорость — векторная величина, равная первой производной по времени от радиуса вектора r рассматриваемой точки: Средняя скорость неравномерного движения (другое название — средняя путевая скорость). Длина пути s, пройденного точкой за промежуток времени от t 1 до t 2, задается интегралом: Если модуль скорости увеличивается с течением времени, то движение называется ускоренным, если же он убывает с течением времени, то движение называется замедленным.

УСКОРЕНИЕ Ускорение — это векторная величина, характеризующая быстроту изменения скорости по модулю и направлению. Среднее ускорение в интервале времени t — векторная величина, равная отношению изменения скорости v интервалу времени t Мгновенное ускорение материальной точки — векторная величина равная первой производной по времени скорости рассматриваемой точки (второй производной по времени от радиуса вектора этой же точки) В общем случае плоского криволинейного движения вектор ускорения удобно представить в виде суммы двух проекций Виды движения
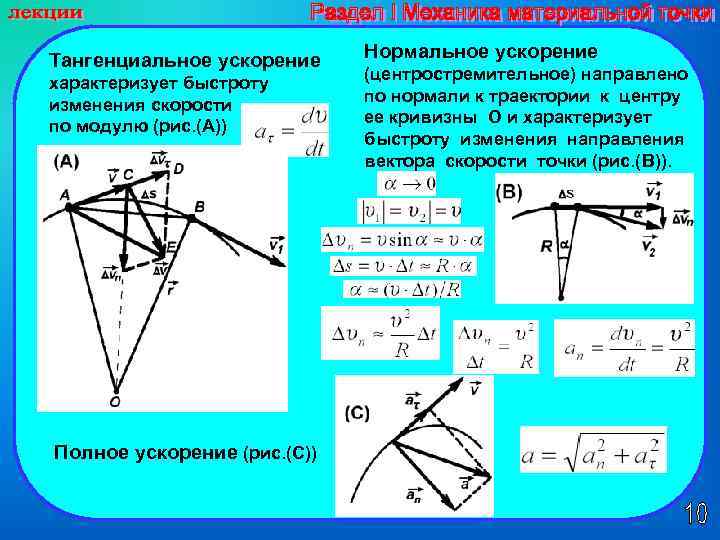
Тангенциальное ускорение характеризует быстроту изменения скорости по модулю (рис. (А)) Полное ускорение (рис. (C)) Нормальное ускорение (центростремительное) направлено по нормали к траектории к центру ее кривизны O и характеризует быстроту изменения направления вектора скорости точки (рис. (B)).

Координатный способ описания движения. Законом движения называется зависимость от времени координат частицы x(t), y(t), z(t). Путь S частицы

Координатный способ описания движения. Скорость V частицы Ускорение а частицы

Естественно-параметрический способ описания движения Дуговой координатой I называется измеренное вдоль траектории расстояние от точки О (начала отсчета) до частицы Скорость частицы Вектор — это единичный вектор, связанный с частицей и направленный по касательной к траектории в сторону возрастания дуговой координаты. Ускорение частицы
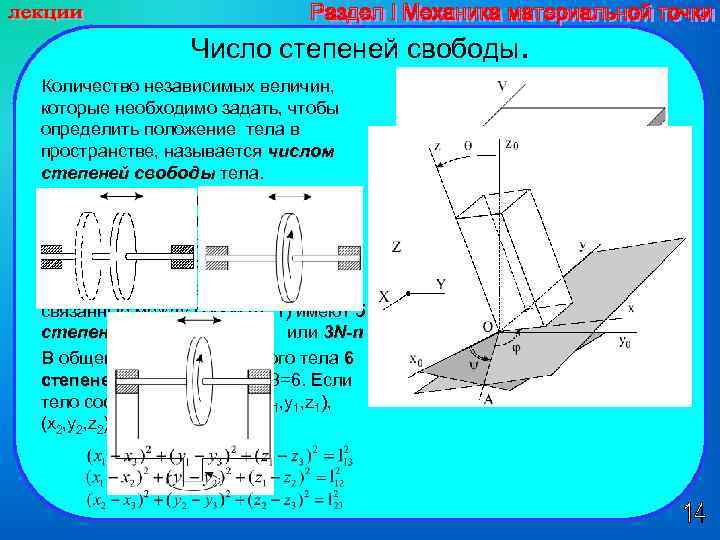
Число степеней свободы. Количество независимых величин, которые необходимо задать, чтобы определить положение тела в пространстве, называется числом степеней свободы тела. степеней свободы Для определения положения в пространстве материальной точки нужно задать три координаты (x, у, z) число степеней свободы равно трем Две материальные точки (N=2), связанные между собой (n=1) имеют 5 степеней свободы 3+3 – 1 или 3 N-n степеней В общем случае для твердого тела 6 степеней свободы 3+3+3 3=6. Если свободы тело состоит из 3 х точек (x 1, y 1, z 1), (x 2, y 2, z 2), (x 3, y 3, z 3)
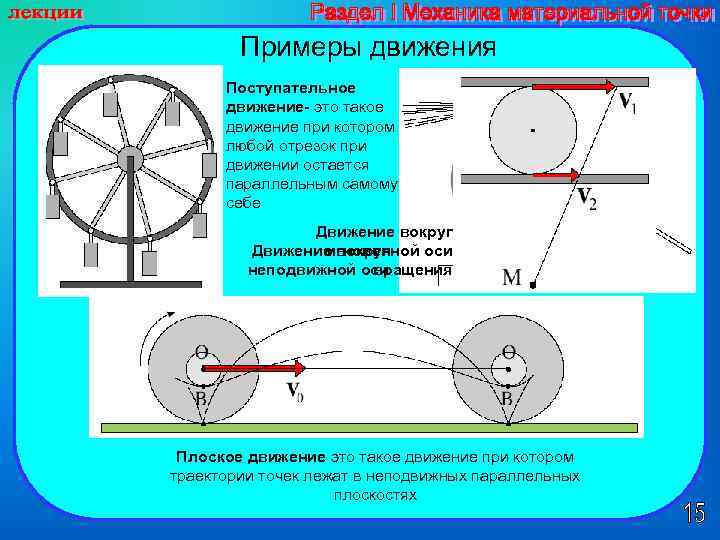
Примеры движения Поступательное движение- это такое движение при котором любой отрезок при движении остается параллельным самому себе Движение вокруг мгновенной оси Движение вокруг вращения неподвижной оси Плоское движение это такое движение при котором траектории точек лежат в неподвижных параллельных плоскостях
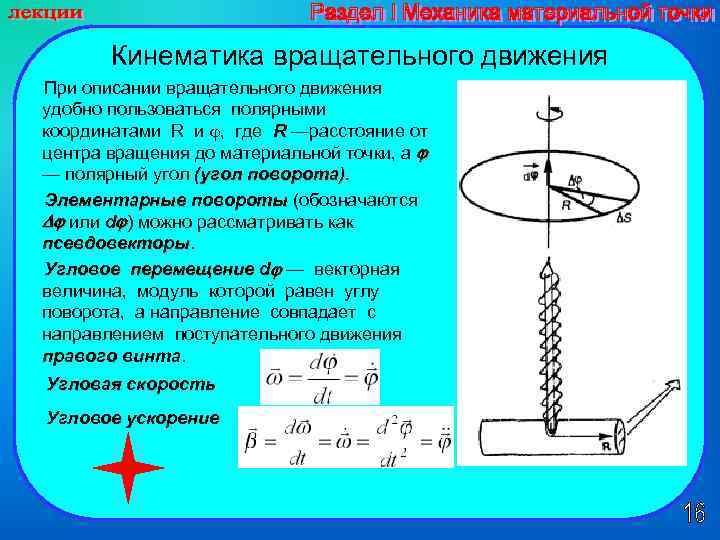
Кинематика вращательного движения При описании вращательного движения удобно пользоваться полярными координатами R и , где R —расстояние от R центра вращения до материальной точки, а — полярный угол (угол поворота). Элементарные повороты (обозначаются Элементарные повороты или d ) можно рассматривать как псевдовекторы Угловое перемещение d — векторная Угловое перемещение величина, модуль которой равен углу поворота, а направление совпадает с направлением поступательного движения правого винта Угловая скорость Угловое ускорение

Кинематика вращательного движения связь между поступательными и вращательными характеристиками Линейная скорость точки связана с угловой скоростью и радиусом траектории соотношением: В векторном виде формулу для линейной скорости можно написать как векторное произведение: При равномерном вращении При равноускоренном вращательном движении Равномерное вращение можно характеризовать периодом вращения T — временем, за которое точка совершает один вращения T полный оборот, Частота вращения — число полных оборотов, совершаемых Частота вращения телом при равномерном его движении по окружности, в единицу времени: Единица частоты вращения — герц (Гц).

Первый закон Ньютона. Закон инерции Галилея Ньютона. Инерциальные системы отсчета. Тело может испытывать внешние воздействия двух типов: а) воздействия, возникающие при непосредственном контакте тел, их соприкосновении (например, давление, трение); б) воздействия со стороны порождаемых телами силовых полей (например, электрического, гравитационного). Свободное тело в динамике, которое не взаимодействует ни с какими другими Свободное тело телами или силовыми полями. Тело называется свободным, если на его свободным положение и движение в пространстве не наложено никаких ограничений, и — несвободным — если на его возможные положения и движения наложены те несвободным или иные ограничения (связи) связи закон инерции Галилея-Ньютона Существует система отсчета, называемая инерциальной, в которой не называемая инерциальной подверженное внешним воздействиям тело (материальная точка) находится в состоянии покоя, либо движется равномерно и прямолинейно. В приведенной формулировке первый закон движения содержит определение инерциальной системы отсчета. Существует бесконечное множество инерциальных систем отсчета. Неинерциальной системой отсчета называется всякая система, движущаяся Неинерциальной системой ускоренно по отношению к инерциальной системе отсчета. В неинерциальной системе отсчета свободное тело движется ускоренно.

Масса и сила Инертностью называется свойство тела оказывать сопротивление Инертностью при попытках привести его в движение или изменить величину и направление его скорости. Масса есть мера инертности тела Свойства массы 1. Аддитивность масса составного тела равна сумме масс его частей. Аддитивность 2. Инвариантность (постоянство). Этим свойством масса обладает только в Инвариантность постоянство) рамках классической механики при движении тел со скоростями, много меньшими скорости света в вакууме. В общем случае масса определяет гравитационные и инерционные свойства тел Сила — векторная величина, являющаяся мерой механического действия на тело со Сила — векторная величина стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет форму и размеры. Прямая, вдоль которой направлена сила, называется линией действия силы Центральными называются силы, которые всюду направлены вдоль прямых, Центральными проходящих через одну и ту же неподвижную точку — центр сил, и зависят только от расстояния до центра сил. Внутренними силами называются силы взаимодействия между частями Внутренними силами рассматриваемой системы. Механическая система называется замкнутой, или изолированной, замкнутой системой, если она не взаимодействует с внешними телами (на нее не действуют внешние силы). внешние силы

Второй закон Ньютона Векторная величина p, равная произведению массы материальной точки на ее скорость, и имеющая направление скорости, называется импульсом, или количеством движения, импульсом, или количеством движения этой материальной точки. Ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки (тела): . Скорость изменения импульса материальной точки равна действующей на нее силе. Векторная величина Fdt называется элементарным импульсом сил F за элементарным импульсом сил F малое время dt ее действия. Законом силы называется конкретный вид Законом силы функции F. Установление закона силы в каждом конкретном случае взаимодействия тел является одной из основных задач физической механики.

Основной закон динамики материальной точки выражает принцип причинности в классической механике — однозначная связь между причинности в классической механике изменением с течением времени состояния движения и положения в пространстве материальной точки и действующие на нее силой, что позволяет, зная начальное состояние материальной точки, вычислить ее состояние в любой последующий момент времени. принцип независимости действия сил: если на материальную точку принцип независимости действия сил действует одновременно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было. Согласно этому принципу силы и ускорения можно разлагать на составляющие, использование которых приводит к существенному упрощению решения задач (принцип суперпозиции). принцип суперпозиции Третий закон Ньютона Всякое действие материальных точек (тел) друг на друга имеет характер взаимодействия; силы с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.
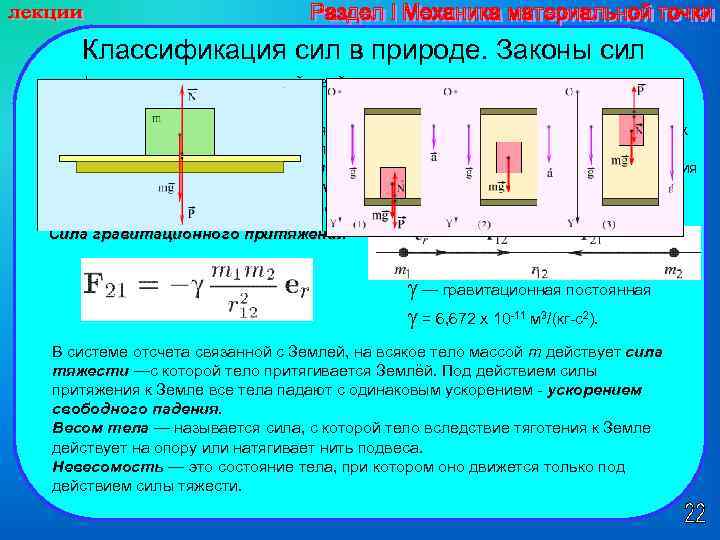
Классификация сил в природе. Законы сил типы фундаментальных взаимодействий гравитационные, электромагнитные, ядерные и слабые • Ядерные и слабые взаимодействия характерны для процессов с участием атомных Ядерные и слабые ядер и элементарных частиц и проявляются на малых расстояниях (~ 10 13 см). малых расстояниях • Электромагнитные и гравитационные силы убывают с увеличением расстояния Электромагнитные и гравитационные силы между взаимодействующими телами медленно потому электромагнитные и гравитационные силы называют дальнодействующими. Сила гравитационного притяжения — гравитационная постоянная = 6, 672 х 10 11 м 3/(кг с2). В системе отсчета связанной с Землей, на всякое тело массой m действует сила тяжести —с которой тело притягивается Землёй. Под действием силы притяжения к Земле все тела падают с одинаковым ускорением свободного падения. Весом тела — называется сила, с которой тело вследствие тяготения к Земле действует на опору или натягивает нить подвеса. Невесомость — это состояние тела, при котором оно движется только под действием силы тяжести.

Классификация сил в природе. Законы сил Упругие силы. Деформация — это изменение формы и размеров твердых тел под Деформация действием внешних сил. Деформация называется упругой, упругой если после прекращения действия внешних сил тело принимает первоначальные размеры и форму. Пластическая деформация — это Пластическая деформация, которая сохраняется в теле после прекращения действия внешних сил. Напряжение σ — физическая величина, численно равная упругой силе Напряжение σ Fel, приходящейся на единицу площади d. S сечения тела: Относительная деформация — количественная мера, характеризующая Относительная деформация степень деформации и определяемая отношением абсолютной деформации ∆x к первоначальному значению величины x , характеризующей форму или размеры тела: относительное изменение длины l стержня (продольная деформация) ε: продольная деформация относительное поперечное растяжение (сжатие) ε′ , где d — диаметр стержня. ε′ (поперечная деформация) поперечная деформация µ — положительный коэффициент, зависящий от свойств материала и называемый коэффициентом Пуассона.

Классификация сил в природе. Законы сил закон Гука При малых деформациях относительная деформация ε пропорциональна напряжению σ: E — коэффициент пропорциональности (модуль упругости), численно модуль упругости равный напряжению, которое возникает при относительной деформации, равной единице. Для случая одностороннего растяжения (сжатия) модуль упругости называется модулем Юнга. закон Гука: удлинение стержня при упругой деформации пропорционально действующей на стержень силе k — коэффициент упругости. Eст ≈ 2· 1011 Н/м 2 Eр ≈ 2· 106 Н/м 2 Кулоновская сила 0 = 8. 85 • 10 12 Ф/м.
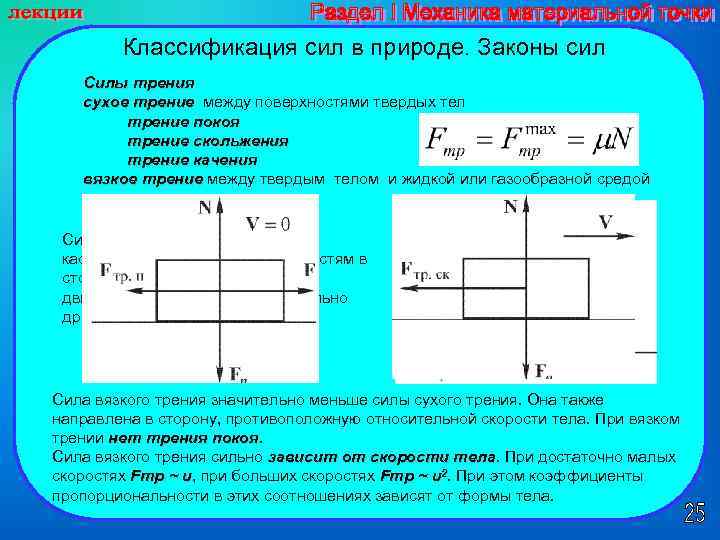
Классификация сил в природе. Законы сил Силы трения сухое трение между поверхностями твердых тел сухое трение покоя трение скольжения трение качения вязкое трение между твердым телом и жидкой или газообразной средой вязкое трение Сила трения направлена по касательной к трущимся поверхностям в сторону, противоположную движению данного тела относительно другого. Сила вязкого трения значительно меньше силы сухого трения. Она также направлена в сторону, противоположную относительной скорости тела. При вязком трении нет трения покоя Сила вязкого трения сильно зависит от скорости тела. При достаточно малых зависит от скорости тела скоростях Fтр ~ υ, при больших скоростях Fтр ~ υ2. При этом коэффициенты Fтр ~ υ пропорциональности в этих соотношениях зависят от формы тела.

Закон сохранения импульса Импульс замкнутой системы не изменяется с течением времени (сохраняется): Закон сохранения импульса является следствием однородности пространства: при параллельном переносе в пространстве замкнутой системытел как целого ее физические свойства не изменяются (не зависят от выбора положения начала координат инерциальной системы отсчета). Закон сохранения импульса можно применять 1. Если система замкнута, т. е. внешние силы отсутствуют 2. Если система незамкнута, но действие внешних сил скомпенсировано 3. Если система незамкнута, но существует направление вдоль которого действие внешних сил скомпенсировано. Тогда для этого направления можно записать закон сохранения импульса 4. Если система незамкнута, но время процесса, в результате которого происходит обмен импульсами между телами, столь мало, что внешняя сила не успевает существенно повлиять на перераспределение импульсов между телами

Закон движения центра масс Центром масс (или центром инерции) системы материальных точек называется воображаемая точка C, положение которой характеризует распределение массы этой системы. где mi и ri — соответственно масса и радиус вектор i й материальной точки; n — число материальных точек в системе Закон движения центра масс: центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему. Из закона сохранения импульса следует, что центр масс замкнутой системы либо движется прямолинейно и равномерно, либо остается неподвижным.

Работа, Мощность Энергия — это универсальная мера различных форм движения и взаимодействия. Энергия Работа силы — это количественная характеристика процесса обмена энергией между Работа силы взаимодействующими телами. При прямолинейном движении тела под действием постоянной силы F которая составляет некоторый угол α с направлением перемещения, работа этой силы равна: В общем случае на элементарном (бесконечно малом) перемещении dr можно ввести скалярную величину — элементарную работу d. A силы F Тогда работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути: Мощность N равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы. Единица работы — джоуль (Дж) – 1 м: 1 Дж=1 Н⋅м. Единица работы Единица мощности — ватт (Вт): 1 Вт — 1 Дж: 1 Вт=1 Дж/с. Единица мощности

Кинетическая энергия механической системы (K) — это энергия механического движения этой системы. Приращение кинетической энергии частицы на элементарном перемещении равно элементарной работе на том же перемещении: Теорема о кинетической энергии для системы: при переходе системы частиц из произвольного начального в произвольное конечное положение работа А всех приложенных к частицам сил равна приращению К кинетической энергии системы: кинетическая энергия: (1) является функцией состояния системы; (2) всегда положительна; (3) неодинакова в разных инерциальных системах отсчета. 0 Теорема Кенига: кинетическую энергию K системы частиц можно представить как сумму двух слагаемых: а) кинетической энергии m. Vc 2/2 воображаемой материальной точки, масса которой равна /2 массе всей системы, а скорость совпадает со скоростью центра масс; б) кинетической энергии Kотн системы частиц, вычисленной в системе центра масс.

Потенциальная энергия механической системы Потенциальная энергия (W) — механическая энергия системы тел, определяемая их Потенциальная энергия взаимным расположением и характером сил взаимодействия между ними. Потенциальная энергия системы является функцией состояния системы. Она функцией состояния системы. зависит только от конфигурации системы и ее положения по отношению к внешним телам. Свойства потенциальной энергии. 1. Потенциальная энергия является функцией только координат x, у, z точки поля, в которой расположена частица: U = U(x, y, z). 2. Работа А сил поля при перемещении частицы из произвольного начального в произвольное конечное положение равна убыли потенциальной энергии частицы А = U 1 - U 2 , U 1, U 2 — потенциальная энергия частицы в начальном и конечном положениях. 3. Потенциальная энергия частицы определена с точностью до произвольной постоянной величины.

Закон сохранения энергии Силы, работа которых при перемещении тела из одного положения в другое, не Силы, зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений, называются консервативными (например, консервативными сила тяготения). Если работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной (например, сила трения). диссипативной Полная механическая энергия системы — энергия механического движения Полная механическая энергия системы и взаимодействия, т. е. равна сумме кинетической и потенциальной энергий. Закон сохранения механической энергии: в системе тел, между Закон сохранения механической энергии: которыми действуют только консервативные силы полная механическая энергия сохраняется, т. е. не изменяется со временем. Это —фундаментальный закон природы. Он является следствием однородности времени — инвариантности физических законов относительно выбора начала отсчета времени. Энергия никогда на исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом заключается физическая сущность закона сохранения и превращения энергии — сущность неуничтожимости материи и ее превращения энергии движения.

Соударения Удар (соударение) — столкновение двух или более тел, при котором Удар (соударение) взаимодействие длится очень короткое время. Центральный удар — при котором тела до удара движутся по прямой, Центральный удар проходящей через их центры масс. Абсолютно упругий удар — столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию. законы сохранения импульса и сохранения механической энергии выполняются Абсолютно неупругий удар — столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое тело. Не выполняется закон сохранения механической энергии: вследствие деформации часть кинетической энергии переходит во внутреннюю энергию тел (разогрев).

Соударения Абсолютно упругий центральный удар шаров Нецентральное упругое соударение шаров одинаковой массы. d – прицельное расстояние

Потенциальное поле сил. Потенциальное поле — поле, в котором работа, совершаемая силами при Потенциальное поле перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений.

Потенциальное поле сил. Поле сил тяготения Закон всемирного тяготения Работа в поле сил тяготения Работа не зависит от траектории перемещения, а Работа не зависит определяется только начальным и конечным положениями тела. потенциальная энергия поля сил тяготения: Потенциалом поля тяготения в данной точке поля Потенциалом поля тяготения называется скалярная величина, равная отношению скалярная потенциальной энергии материальной точки, помещенной в рассматриваемую точку поля, к массе материальной точки:

Потенциальное поле сил. Поле сил тяготения Напряженность поля тяготения это физическая величина, равная Напряженность поля тяготения отношению силы, действующей со стороны поля на помещенное в него тело (материальную точку), к массе этого тела. Напряженность является векторной силовой характеристикой поля тяготения. Первая космическая скорость Вторая космическая скорость Третья космическая скорость

Элементы специальной теории относительности Преобразования Галилея В классической механике, при скоростях тел значительно меньших, чем скорость света (c << υ) , справедлив механический принцип относительности (принцип относительности Галилея): законы динамики одинаковы во всех инерциальных системах отсчета. Инерциальная неподвижная система K (с Правило сложения скоростей в классической координатами x, y, z)механике: Система K′ (с координатами x ' , y ' , z ' ), движущуюся относительно K равномерно и прямолинейно с постоянной скоростью u В начальный момент времени начала координат O и O′ этих систем совпадают. В произвольный момент времени t: r 0 =ut Для произвольной точки A: Эти соотношения называются преобразованиями координат Галилея. к преобразованиям Галилея нужно добавить соотношение:

ОГРАНИЧЕННОСТЬ ЗАКОНОВ КЛАССИЧЕСКОЙ МЕХАНИКИ Основные постулаты и противоречия 1. Физическое пространство однородно и изотропно. Пространство и время существуют сами пор себе и независимо от материальных тел 4. Масса материальной точки не зависит от скорости движения Масса частиц зависит от скорости 2. Все механически явления протекают одинаково в любой инерциальной системе отсчета 3. Взаимодействие между физическим объектами происходит мгновенно (скорость бесконечно большая) 5. Все кинематические Скорость света не зависит от системы характеристики можно измерить При затмении Солнца наблюдалось сколь угодно точно координат и является предельной отклонение солнечных лучей от Выполняются соотношения прямолинейного распространения неопределенностей (кривизна пространства)

Элементы специальной теории относительности Постулаты Эйнштейна. 1) Принцип относительности: никакие опыты, проведенные внутри данной инерциальной системы отсчета, не дают возможность обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной системы отсчета к другой. 2) Принцип инвариантности скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета.

Элементы специальной теории относительности Преобразования Лоренца Пусть система O′ движется относительно системы O со скоростью υ =const, причем c ≈ υ ( − c скорость света Обозначим отношение скоростей υ и c через β = υ/c. Пусть вектор скорости υ направлен вдоль оси OX. Тогда координат и времени будут иметь вид: Эти преобразования Лоренца — при c << υ они переходят в преобразования Галилея. Преобразования Лоренца (релятивистские преобразования) устанавливают взаимосвязь пространства и времени — в закон преобразования координат входит время, а в закон преобразования времени — пространственные координаты.

Элементы специальной теории относительности Следствия из преобразований Лоренца 1. Длительность события, происходящего в некоторой точке, Длительность события наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Следовательно, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов. 2. Размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движения, причем лоренцово сокращение длины тем больше, чем больше скорость движения. Поперечные размеры тел не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета.

Элементы специальной теории относительности 3. Если материальная точка движется в системе O′ вдоль оси x′ со скоростью υ′ , а сама система O′ движется со скоростью υ′ u относительно системы O, то релятивистский закон сложения скоростей: 4. В качестве величины, инвариантной по отношению к преобразованию координат в четырехмерном пространстве Эйнштейна (не зависящей от выбора системы отсчета) вводится интервал между событиями: интервал между событиями расстояние между точками обычного трехмерного пространства.

Элементы специальной теории относительности Основные соотношения релятивистской динамики 1. Релятивистская масса m движущихся релятивистских частиц (тел) зависит от их скорости. m 0 — масса покоя частицы, т. е. масса, измеренная в той инерциальной системе отсчета, в которой частица находится в покое. 2. Релятивистский импульс p. Релятивистский импульс системы сохраняется. Закон сохранения релятивистского импульса — следствие однородности пространства. 3. Основной закон релятивистской динамики: Законы классической динамики получаются из законов релятивистской динамики в предельном случае υ << c. << 4. Полная энергия тела массы m: Соотношение носит универсальный характер, оно применимо ко всем формам энергии, т. е. можно утверждать, что с энергией, какой бы формы она не была, связана масса и, наоборот, со всякой массой связана энергия. Покоящееся тело обладает энергией покоя. Полная энергия замкнутой системы сохраняется. Закон сохранения энергии — следствие однородности времени.

Элементы специальной теории относительности Основные соотношения релятивистской динамики 5. Кинетическая энергия: 7. В случае, когда масса покоя частицы равна нулю, то частицы равна нулю 6. Релятивистское соотношение между полной энергией и импульсом тела: Следовательно, такая частица может обладать отличными от нуля энергией и импульсом только в том случае, когда она движется со скоростью света. К таким частицам относятся фотоны Основной вывод теории относительности — пространство и время органически взаимосвязаны и образуют единую форму существования материи — пространство-время.

Движение относительно неинерциальных систем отсчета Скорость и ускорение частицы А в неподвижной системе отсчета называют абсолютной скоростью Vабс и абсолютным ускорением аабс, Скорость и ускорение в движущейся системе отсчета — относительной скоростью Vотн и относительным ускорением аотн.

Движение относительно неинерциальных систем отсчета

Движение относительно неинерциальных систем отсчета

Движение относительно неинерциальных систем отсчета Свободное не подверженное внешним воздействиям тело в неинерциальной системе отсчета движется с отличным от нуля ускорением, отличным от нуля ускорением несмотря на то что силы взаимодействия с другими телами отсутствуют (F = 0) Уравнение движения тела в инерциальной системе

Движение относительно неинерциальных систем отсчета поступательная сила инерции: центробежная сила инерции сила Кориолиса Уравнение называется уравнением движения частицы в неинерциальной системе отсчета.

Движение относительно неинерциальных систем отсчета • Силы инерции возникают не из за взаимодействия тел, а вследствие ускоренного движения системы отсчета. ускоренного движения • Силы инерции изменяются при переходе от одной неинерциальной системы отсчета к другой, они не инвариантны относительно такого не инвариантны перехода. • Силы инерции не подчиняются третьему закону Ньютона. не подчиняются • Все силы инерции, подобно силам тяготения, пропорциональны массе тела. Пример. Вагон движется с ускорением a по Пример. 0 прямолинейному горизонтальному участку дороги. К потолку вагона на нити подвешен груз массой т. Найти угол отклонения нити от вертикали.

Движение относительно неинерциальных систем отсчета На расположенное вблизи поверхности Земли тело массой т, скорость которого по отношению к Земле равна нулю, действует центробежная сила инерции Fцб, и сила гравитационного притяжения цб Frp, направленная к центру Земли и равная по модулю Центробежная сила инерции направлена перпендикулярно оси вращения Земли. gэкв = 9, 780 м/с2 gпол= 9, 832 м/с2

Движение относительно неинерциальных систем отсчета Сила Кориолиса возникает, если тело Сила Кориолиса движется относительно неинерциальной вращающейся системы отсчета. Вектор Fкор перпендикулярен к вектору скорости Vотн и вектору угловой скорости . Наличием силы Кориолиса объясняются такие явле ния, ак отклонение свободно к падающих тел к востоку, раз мыв равых п берегов текущих северных рек и др. Пример. Найдем силу бокового давления, Пример. с которой поезд массой т, который движется со скоростью V вдоль меридиана в направлении с севера на юг, действует на рельсы Сила бокового давления возникает за счет действия на поезд силы Кориолиса, величина которой равна

ВОПРОСЫ ВЫНОСИМЫЕ НА КОЛЛОКВИУМ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. Кинематические характеристики поступательного и вращательного движения материальной точки Способы описания движения (краткая характеристика). Динамика поступательного движения. Законы Ньютона и силы в природе Центр масс системы и закон его движения Работа, энергия и мощность Поле сил - основные понятия Взаимодействие материальных точек, виды столкновений Принцип относительности Галилея и постулаты Эйнштейна Преобразования Лоренца и следствия из них Основные соотношения релятивистской механики Силы инерции. Закон движения в неинерциальных системах отсчета

Движение относительно неинерциальных систем отсчета
МОДУЛЬ 1 механика мат точки 2009.ppt