Учебный курс Компьютерное моделирование полупроводников 5 курс доцент

Зарегистрируйтесь, чтобы просмотреть полный документ!

Учебный курс: «Компьютерное моделирование полупроводников» (5 курс) доцент кафедры физики низкоразмерных структур ИФИТ ДВФУ, кандидат физико-математических наук Луняков Юрий Вилорьевич, т. 2679875 (+7 902 481 9875) е-mail: luniakov@iacp. dvo. ru Сайт с информационными материалами для самостоятельного изучения: ftp: //ftp. dvo. ru/pub/Computers/ 1

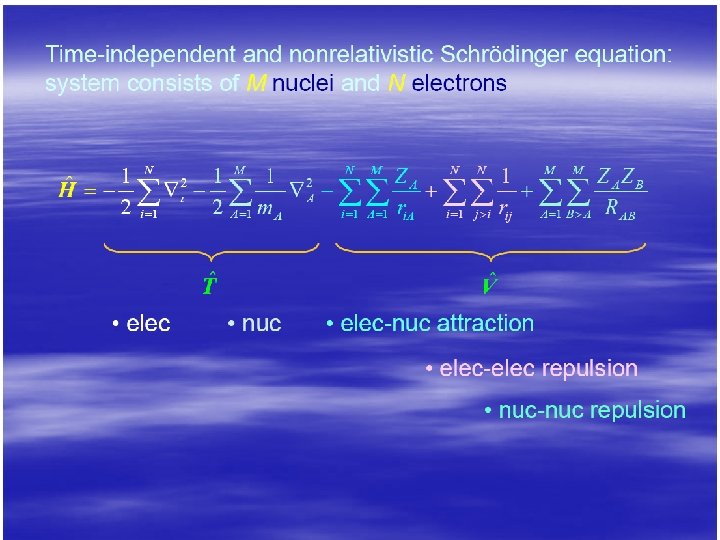
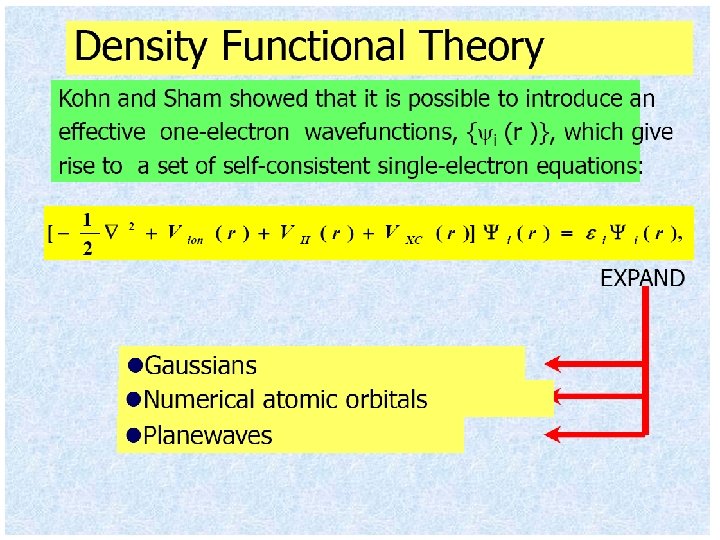
Электронное уравнение: где первый член в сумме – кинетическая энергия электронов (Te), второй – потенциал взаимодействия между электронами и ядрами (Vne), а третий – потенциал взаимодействия между электронами (Vee). Потенциалом взаимодействия между ядрами (Vnn) мы при дальнейшем рассмотрении пренебрегаем в силу того, что для каждой фиксированной конфигурации ядер это величина постоянная. Если бы не было члена Vee, то гамильтониан сводился бы к: где h(i) – одноэлектронный оператор. φ'i(i) – одноэлектронная функция (орбиталь), являющаяся решением одноэлектронного уравнения: Поскольку электронный гамильтониан не зависит от спиновых операторов в используемом пока представлении, то орбиталь с учетом спина можно записать в виде φ'i(i)σ, где σ указывает на спин (1/2 или – 1/2).

Метод Хартри-Фока-Рутана Одноэлектронные волновые функции i(r) ïðåäñòàâëÿþòñÿ â âèäå ðàçëîæåíèÿ ïî íåêîòîðîìó áàçèñíîìó íàáîðó àòîìíûõ âîëíîâûõ ôóíêöèé j(r): При подстановке в уравнения Хартри-Фока получаем По ходу вычисления матричных элементов приходится вычислять большое количество интегралов типа:

Полуэмпирические методы PRDDO, Partial Retention of Diatomic Differential Overlap) сохранение одно, двух и трехцентровых кулоновских интегралов и двухцентровых обменных, N 3 scaling. (ZDO, Zero Differential Overlap) CNDO, Complete Neglect of Differential Overlap – для всех пар атомных орбиталей INDO, Intermediate Neglect of Differential Overlap учитывает одноцентровые кулоновские < µµ|µµ > и обменные < µ |µ > интегралы и двухцентровые кулоновские интегралы < µµ| >. MINDO, Modified Intermediate Neglect of Differential Overlap: MINDO/2 , MINDO/3 (MNDO, Modified Neglect of Diatomic Overlaps (NDDO, Neglect of Diatomic Differential Overlap)

Эмпирические методы где µ — фиктивная масса, ассоциированная с электронными волновыми функциями, E — функционал энергии Кона-Шема, RI — позиция иона I, n определяет размер и форму единичной ячейки.

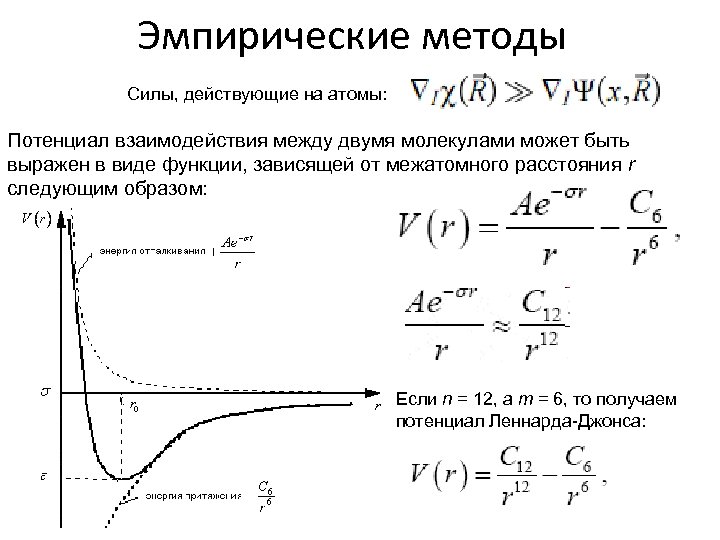
Эмпирические методы Силы, действующие на атомы: Потенциал взаимодействия между двумя молекулами может быть выражен в виде функции, зависящей от межатомного расстояния r следующим образом: Если n = 12, а m = 6, то получаем потенциал Леннарда-Джонса:

Некоторые двухчастичные потенциалы Потенциал Бакингема Леннарда-Джонса Гармонический Морзе Стиллинджера. Вебера (SW 2) Формула

Из физических соображений очевидно, что компоненты решёточной энергии можно разделить на определяемые дальнодействующими (электростатическими) и короткодействующими (межатомными) потенциалами. Эти компоненты нуждаются в раздельном вычислении. Для систем малых и средних размеров наиболее эффективный путь для расчета электростатической энергии — суммирование методом Эвальда. Результирующее выражение для энергии может быть представлено в виде двух быстросходящихся сумм в обратном и реальном пространствах: Etotal = Erecip + Ereal Erecip = Ereal = где G — вектор решётки в обратном пространстве, rij — межатомные расстояния, qi и qj — заряды на атомах, — параметр, управляющий распределением сумм между прямым и обратным пространствами, erfc{} — дополнительная функция ошибок.