Учебные пособия для 2 семестра Пособия подготовлены

Учебные пособия для 2 семестра § Пособия подготовлены преподавателями кафедры физики 1

Лекция 2. Закон сохранения импульса 2

Вопросы: § Инерциальная система отсчета. Принцип относительности Галилея § Основные законы ньютоновской динамики § Силы. Виды сил и их закономерности § Динамика материальной точки § Механическая система и ее центр масс § Закон сохранения импульса механической системы 3

Введение § Рассмотрением причин изменения состояния движения занимается часть механики, называемая динамикой. Ее основой служат три закона Ньютона, применяемые для описания движения частицы. С точки зрения построения динамики они играют такую же роль, как и аксиомы Евклида в геометрии. Существенное отличие состоит в том, что законы Ньютона основаны на обобщении экспериментальных фактов и наблюдений за окружающим нас материальным миром. 4

Инерциальная система отсчета. Принцип относительности Галилея § 5

Инерциальная система отсчета. Принцип относительности Галилея § 6

Инерциальная система отсчета. Принцип относительности Галилея § 7

Инерциальная система отсчета. Принцип относительности Галилея § Первоначальными опытами было установлено, что ИСО является Земля. Последующие более точные опыты показали, что эта система отсчета не совсем инерциальная: были обнаружены ускорения, существование которых нельзя объяснить действием каких-либо определенных тел – необходимо учитывать вращение Земли и ее движение вокруг Солнца (опыт Фуко по сохранению неизменной плоскости качания маятника с шаровым подвесом без трения и все аналогичные ему). Заметим, что во многих случаях систему отсчета, связанную с Землей, можно считать практически инерциальной. § Наблюдения астрономов за планетами показали инерциальность гелиоцентрической системы отсчета (система Коперника, в честь Николая Коперника, 1473 -1543), связанной с центром Солнца и тремя «неподвижными» звездами. 8

Инерциальная система отсчета. Принцип относительности Галилея § 9

Инерциальная система отсчета. Принцип относительности Галилея § Также любая другая система отсчета, движущаяся равномерно и прямолинейно относительно гелиоцентрической системы, является инерциальной. § Существует не одна, а бесчисленное множество инерциальных систем отсчета, движущихся относительно друга прямолинейно и равномерно. § Системы отсчета, движущиеся с ускорением относительно инерциальных систем, называют неинерциальными. 10

Инерциальная система отсчета. Принцип относительности Галилея § Важной особенностью инерциальных систем отсчета является наличие свойств симметрии пространства и времени. § Опыт убеждает, что в этих системах отсчета время однородно, а пространство однородно и изотропно. Свойства симметрии пространства и времени тесно связаны с законами сохранения и определяют, что их должно быть три. § Однородность времени заключается в том, что протекание физических явлений (в одних и тех же условиях) в разное время их наблюдения одинаково. Иначе говоря, различные моменты времени эквивалентны другу по своим физическим свойствам. § Однородность и изотропность пространства заключаются в том, что свойства пространства одинаковы в различных точках (однородность), а для каждой точки свойства одинаковы во всех от нее направлениях (изотропность). § Примечание. По отношению к неинерциальным системам отсчета пространство не является однородным и изотропным. 11

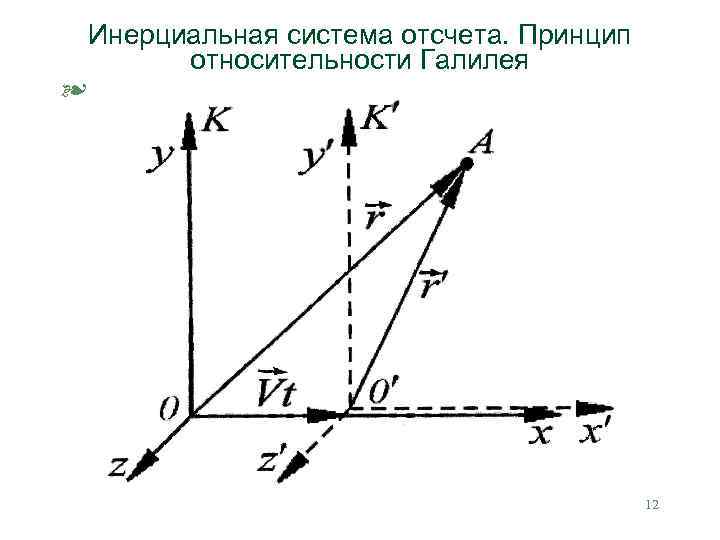
Инерциальная система отсчета. Принцип относительности Галилея § 12

Инерциальная система отсчета. Принцип относительности Галилея 13

Инерциальная система отсчета. Принцип относительности Галилея 14

Основные законы ньютоновской динамики н 15

Основные законы ньютоновской динамики 16

Основные законы ньютоновской динамики § 17

Основные законы ньютоновской динамики 18

Основные законы ньютоновской динамики 19

Основные законы ньютоновской динамики 20

Основные законы ньютоновской динамики 21

Силы. Виды сил и их закономерности Чтобы свести нахождение закона движения материальной точки к чисто математической задаче, т. е. записать уравнение движения – необходимо знать действующую на точку силу, иначе говоря, зависимость силы от определяющих ее величин. В классической механике приходится иметь дело с: • гравитационными силами; • электромагнитными силами; • упругими силами; • силами трения; • силами сопротивления. Гравитационные и электромагнитные силы – фундаментальные силы (определяются фундаментальными взаимодействиями), их нельзя свести к более простым силам. Упругие силы и силы трения являются по своей природе электромагнитными и не могут считаться фундаментальными, для них существуют приближенные эмпирические формулы. 22