422379dc06eb4ef3700d93b081e12152.ppt
- Количество слайдов: 19
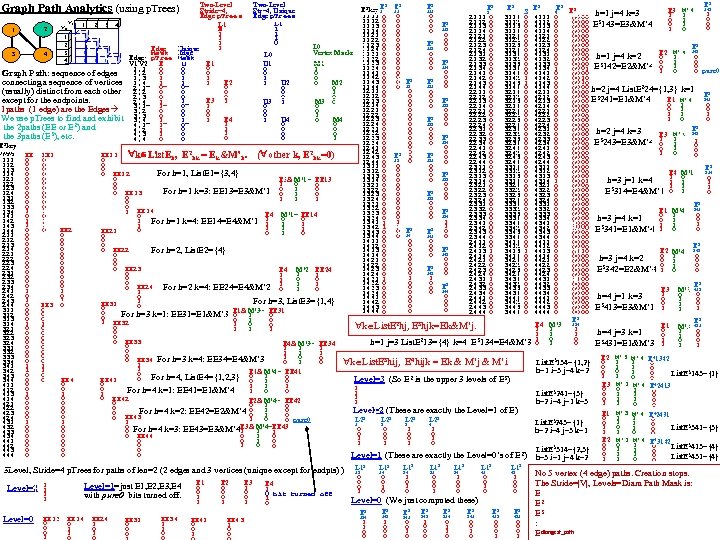 Two-Level Str=4, Unique Edge p. Trees L 1 1 0 Two-Level Stride=4, Edge p. Trees L 1 E 1 1 Edge Unique Mask Edge p. Tree Mask Edges E 1 U E V 1 V 2 0 0 0 1, 1 0 0 0 1, 2 1 1, 3 1 1_ 1, 4_ 1_ E 2 0 0 0 2, 1 0 0 0 2, 2 0 0 0 2, 3 1_ E 3 1 2, 4_ 1_ 1 0 1 3, 1 0 0 0 3, 2 0 0 0 3, 3 E 4 1 1_ 3, 4_ 1_ 1 0 1 4, 1 1 0 1 4, 2 1 0 1 4, 3 0 0 0 4, 4 Graph Path Analytics (using p. Trees) 2 1 3 4 V 1 V 2 1 2 3 4 1 1 1 2 1 3 4 1 Graph Path: sequence of edges connecting a sequence of vertices (usually) distinct from each other except for the endpoints. 1 paths (1 edge) are the Edges We use p. Trees to find and exhibit the 2 paths (EE or E 2) and the 3 paths (E 3), etc. E 2 key v 1 v 2 v 3 111 112 113 114 121 122 123 124 131 132 133 134 141 142 143 144 211 212 213 214 221 222 223 224 231 232 233 234 241 242 243 244 311 312 313 314 321 322 323 324 331 332 333 334 341 342 343 344 411 412 413 414 421 422 423 424 431 432 433 434 441 442 443 444 EE 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 L 0 U 1 0 0 1 1 U 3 0 0 0 1 U 2 0 0 0 1 U 4 0 0 3 L 0 Vertex Masks M 1 1 0 0 0 M 3 0 0 1 0 M 2 0 1 0 0 M 4 0 0 0 1 EE 11 k List. Eh, E 2 hk = Ek&M’h. ( other k, E 2 hk=0) 0 0 0 For h=1, List. E 1={3, 4} 0 EE 12 0 E 3& M’ 1= EE 13 0 1 0 0 For h=1 k=3: EE 13=E 3&M’ 1 0 EE 13 0 1 0 0 1 1 1 0 0 1 EE 14 E 4 M’ 1= EE 14 0 0 0 1 For h=1 k=4: EE 14=E 4&M’ 1 1 1 1 1 0 EE 21 0 0 0 EE 22 For h=2, List. E 2={4} 0 0 EE 23 E 4 M’ 2 EE 24 0 1 1 1 0 0 0 1 1 0 EE 24 For h=2 k=4: EE 24=E 4&M’ 2 1 1 0 0 1 For h=3, List. E 3={1, 4} EE 31 0 0 0 For h=3 k=1: EE 31=E 1&M’ 3 E 1& M’ 3= EE 31 0 0 0 1 EE 32 1 0 0 0 1 1 1 0 0 0 EE 33 E 4& M’ 3= EE 34 0 1 1 1 0 1 0 0 0 EE 34 For h=3 k=4: EE 34=E 4&M’ 3 0 1 1 E 1& M’ 4= EE 41 0 0 For h=4, List. E 4={1, 2, 3} 0 EE 41 1 0 0 1 1 1 0 0 For h=4 k=1: EE 41=E 1&M’ 4 1 0 EE 42 E 2& M’ 4= EE 42 0 0 1 0 0 0 For h=4 k=2: EE 42=E 2&M’ 4 0 1 0 0 EE 43 1 0 0 pure 0 1 0 For h=4 k=3: EE 43=E 3&M’ 4 E 3& M’ 4=EE 43 1 1 0 1 0 EE 44 0 0 0 1 0 0 EE 1 0 0 0 1 1 0 EE 2 0 0 0 1 0 1 EE 3 0 0 1 0 0 0 0 1 1 0 EE 4 0 0 0 1 0 0 0 0 0 Level=0 1 1 EE 13 0 0 0 1 Level=1=just E 1, E 2, E 3, E 4 with pure 0 bits turned off. EE 14 0 1 1 0 EE 24 1 0 EE 31 0 0 0 EE 34 1 1 0 0 E 1 0 0 1 1 EE 41 0 0 1 E 2 0 0 0 1 EE 43 1 0 0 E 3 1 0 0 1 E 4 1 0 bit turned off 1 0 E 3 11 0 0 0 0 3 0 E 0 12 0 0 0 0 E 3 0 13 0 0 0 0 1 1 3 0 E 0 14 0 0 0 0 1 0 0 0 0 E 3 111 0 0 E 3 113 0 0 E 3 121 0 0 E 3 123 0 0 E 3 131 0 0 E 3 133 0 0 E 3 141 0 0 E 3 143 1 0 0 0 2111 2112 2113 2114 2121 2122 2123 2124 2131 2132 2133 2134 2141 2142 2143 2144 2211 2212 2213 2214 2221 2222 2223 2224 2231 2232 2233 2234 2241 2242 2243 2244 2311 2312 2313 2314 2321 2322 2323 2324 2331 2332 2333 2334 2341 2342 2343 2344 2411 2412 2413 2414 2421 2422 2423 2424 2431 2432 2433 2434 2441 2442 2443 2444 E 3 112 0 0 E 3 114 0 0 E 3 122 0 0 E 3 124 0 0 E 3 132 0 0 E 3 134 1 1 0 0 E 3 142 0 0 E 3 144 0 0 E 3 2 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 E 3 3111 3112 3113 3114 3121 3122 3123 3124 3131 3132 3133 3134 3141 3142 3143 3144 3211 3212 3213 3214 3221 3222 3223 3224 3231 3232 3233 3234 3241 3242 3243 3244 3311 3312 3313 3314 3321 3322 3323 3324 3331 3332 3333 3334 3341 3342 3343 3344 3411 3412 3413 3414 3421 3422 3423 3424 3431 3432 3433 3434 3441 3442 3443 3444 3 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 k List. E 2 hj, E 3 hjk=Ek&M’j. h=1 j=3 List. E 213={4} k=4 E 3134=E 4&M’ 3 k List. E 3 hij, E 4 hijk = Ek & M’j & M’i 3 Level, Stride=4 p. Trees for paths of len=2 (2 edges and 3 vertices (unique except for endpts) ) Level=2 E 3 key E 1 1111 0 1112 0 1113 0 1114 0 1121 0 1122 0 1123 0 1124 0 1131 0 1132 0 1133 0 1134 0 1141 0 1142 0 1143 0 1144 0 1211 0 1212 0 1213 0 1214 0 1221 0 1222 0 1223 0 1224 0 1231 0 1232 0 1233 0 1234 0 1241 0 1242 0 1243 0 1244 0 1311 0 1312 0 1313 0 1314 0 1321 0 1322 0 1323 0 1324 0 1331 0 1332 0 1333 0 1334 0 1341 1 1342 1 1343 0 1344 0 1411 0 1412 0 1413 0 1414 0 1421 0 1422 0 1423 0 1424 0 1431 1 1432 0 1433 0 1434 0 1441 0 1442 0 1443 0 1444 0 List. E 3134={1, 2} h=1 i=3 j=4 k=2 Level=3 (So E 2 is the upper 3 levels of E 3) 1 1 Level=2 (These are exactly the Level=1 of E) L 23 1 0 0 1 1 L 23 2 0 0 0 1 L 23 3 1 0 0 1 L 23 4 1 0 L 13 14 0 0 1 0 L 13 24 1 0 E 3 134 1 1 0 0 E 3 143 1 0 0 0 E 3 241 0 0 1 0 L 13 31 0 0 0 1 L 13 34 1 0 0 0 L 13 41 0 0 1 0 L 13 43 1 0 0 0 Level=0 (We just computed these) E 3 243 1 0 0 0 List. E 3241={3} h=2 i=4 j=1 k=3 List. E 3243={1} h=2 i=4 j=3 k=1 Level=1 (These are exactly the Level=0’s of E 2) L 13 13 0 0 0 1 E 3 E 3 M’ 4 143 4 1 1 1 0 00 00 h=1 j=4 k=3 0 0 1 0 00 00 E 3143=E 3&M’ 4 0 0 1 0 00 00 0 1 0 0 00 00 E 3 0 00 00 E 2 M’ 4 142 0 00 00 h=1 j=4 k=2 0 0 1 0 00 00 00 E 3142=E 2&M’ 4 0 1 0 0 1 1 00 01 0 pure 0 1 0 0 00 00 10 0 00 00 h=2 j=4 List. E 224={1, 3} k=1 0 00 00 E 3241=E 1&M’ 4 241 E 1 M’ 4 0 00 00 0 0 1 0 00 00 1 1 1 0 00 00 0 1 0 0 00 00 E 3 0 00 00 h=2 j=4 k=3 243 0 00 0 0 E 3 M’ 4 0 00 00 3 1 1 1 0 00 00 E 243=E 3&M’ 4 0 1 0 0 00 00 1 0 00 00 E 3 0 00 00 314 E 4 M’ 1 0 00 00 1 0 0 h=3 j=1 k=4 1 00 01 1 0 00 00 1 3314=E 4&M’ 1 1 1 0 00 00 0 1 E 0 0 00 00 E 3 0 00 00 E 1 M’ 4 341 0 00 00 0 0 1 0 00 00 h=3 j=4 k=1 0 0 10 00 1 1 1 0 10 00 E 3341=E 1&M’ 4 1 0 00 00 0 0 E 3 0 00 00 E 2 M’ 4 342 0 01 10 0 1 0 0 00 00 h=3 j=4 k=2 0 1 0 0 00 00 E 3342=E 2&M’ 4 1 0 0 00 00 0 11 00 00 E 3 0 00 00 E 3 M’ 1 413 0 00 00 h=4 j=1 k=3 1 0 00 0 0 1 0 00 00 E 3413=E 3&M’ 1 1 0 00 00 3 E E 3 E 4 M’ 3 134 E 1 M’ 3 431 1 0 0 1 h=4 j=3 k=1 1 0 0 1 E 3431=E 1&M’ 3 1 0 1 1 1 E 3 4111 4112 4113 4114 4121 4122 4123 4124 4131 4132 4133 4134 4141 4142 4143 4144 4211 4212 4213 4214 4221 4222 4223 4224 4231 4232 4233 4234 4241 4242 4243 4244 4311 4312 4313 4314 4321 4322 4323 4324 4331 4332 4333 4334 4341 4342 4343 4344 4411 4412 4413 4414 4421 4422 4423 4424 4431 4432 4433 4434 4441 4442 4443 4444 E 3 314 0 1 1 0 E 3 341 0 0 1 0 E 3 413 0 0 0 1 E 3 431 0 0 0 1 List. E 3314={2, 3} h=3 i=1 j=4 k=2 E 2 0 0 0 1 E 3 0 0 0 1 E 1 0 0 1 1 E 2 0 0 0 1 M’ 3 1 1 0 1 M’ 1 0 1 1 1 M’ 4 1 1 1 0 E 41342 0 0 0 List. E 3143={1} 0 42413 E 0 0 E 42431 0 0 List. E 3341={3} 0 0 E 43142 0 List. E 3413={4} 0 0 List. E 3431={4} 0 No 5 vertex (4 edge) paths. Creation stops. The Stride=|V|, Levels=Diam Path Mask is: E E 2 E 3 : Edlongest_path
Two-Level Str=4, Unique Edge p. Trees L 1 1 0 Two-Level Stride=4, Edge p. Trees L 1 E 1 1 Edge Unique Mask Edge p. Tree Mask Edges E 1 U E V 1 V 2 0 0 0 1, 1 0 0 0 1, 2 1 1, 3 1 1_ 1, 4_ 1_ E 2 0 0 0 2, 1 0 0 0 2, 2 0 0 0 2, 3 1_ E 3 1 2, 4_ 1_ 1 0 1 3, 1 0 0 0 3, 2 0 0 0 3, 3 E 4 1 1_ 3, 4_ 1_ 1 0 1 4, 1 1 0 1 4, 2 1 0 1 4, 3 0 0 0 4, 4 Graph Path Analytics (using p. Trees) 2 1 3 4 V 1 V 2 1 2 3 4 1 1 1 2 1 3 4 1 Graph Path: sequence of edges connecting a sequence of vertices (usually) distinct from each other except for the endpoints. 1 paths (1 edge) are the Edges We use p. Trees to find and exhibit the 2 paths (EE or E 2) and the 3 paths (E 3), etc. E 2 key v 1 v 2 v 3 111 112 113 114 121 122 123 124 131 132 133 134 141 142 143 144 211 212 213 214 221 222 223 224 231 232 233 234 241 242 243 244 311 312 313 314 321 322 323 324 331 332 333 334 341 342 343 344 411 412 413 414 421 422 423 424 431 432 433 434 441 442 443 444 EE 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 L 0 U 1 0 0 1 1 U 3 0 0 0 1 U 2 0 0 0 1 U 4 0 0 3 L 0 Vertex Masks M 1 1 0 0 0 M 3 0 0 1 0 M 2 0 1 0 0 M 4 0 0 0 1 EE 11 k List. Eh, E 2 hk = Ek&M’h. ( other k, E 2 hk=0) 0 0 0 For h=1, List. E 1={3, 4} 0 EE 12 0 E 3& M’ 1= EE 13 0 1 0 0 For h=1 k=3: EE 13=E 3&M’ 1 0 EE 13 0 1 0 0 1 1 1 0 0 1 EE 14 E 4 M’ 1= EE 14 0 0 0 1 For h=1 k=4: EE 14=E 4&M’ 1 1 1 1 1 0 EE 21 0 0 0 EE 22 For h=2, List. E 2={4} 0 0 EE 23 E 4 M’ 2 EE 24 0 1 1 1 0 0 0 1 1 0 EE 24 For h=2 k=4: EE 24=E 4&M’ 2 1 1 0 0 1 For h=3, List. E 3={1, 4} EE 31 0 0 0 For h=3 k=1: EE 31=E 1&M’ 3 E 1& M’ 3= EE 31 0 0 0 1 EE 32 1 0 0 0 1 1 1 0 0 0 EE 33 E 4& M’ 3= EE 34 0 1 1 1 0 1 0 0 0 EE 34 For h=3 k=4: EE 34=E 4&M’ 3 0 1 1 E 1& M’ 4= EE 41 0 0 For h=4, List. E 4={1, 2, 3} 0 EE 41 1 0 0 1 1 1 0 0 For h=4 k=1: EE 41=E 1&M’ 4 1 0 EE 42 E 2& M’ 4= EE 42 0 0 1 0 0 0 For h=4 k=2: EE 42=E 2&M’ 4 0 1 0 0 EE 43 1 0 0 pure 0 1 0 For h=4 k=3: EE 43=E 3&M’ 4 E 3& M’ 4=EE 43 1 1 0 1 0 EE 44 0 0 0 1 0 0 EE 1 0 0 0 1 1 0 EE 2 0 0 0 1 0 1 EE 3 0 0 1 0 0 0 0 1 1 0 EE 4 0 0 0 1 0 0 0 0 0 Level=0 1 1 EE 13 0 0 0 1 Level=1=just E 1, E 2, E 3, E 4 with pure 0 bits turned off. EE 14 0 1 1 0 EE 24 1 0 EE 31 0 0 0 EE 34 1 1 0 0 E 1 0 0 1 1 EE 41 0 0 1 E 2 0 0 0 1 EE 43 1 0 0 E 3 1 0 0 1 E 4 1 0 bit turned off 1 0 E 3 11 0 0 0 0 3 0 E 0 12 0 0 0 0 E 3 0 13 0 0 0 0 1 1 3 0 E 0 14 0 0 0 0 1 0 0 0 0 E 3 111 0 0 E 3 113 0 0 E 3 121 0 0 E 3 123 0 0 E 3 131 0 0 E 3 133 0 0 E 3 141 0 0 E 3 143 1 0 0 0 2111 2112 2113 2114 2121 2122 2123 2124 2131 2132 2133 2134 2141 2142 2143 2144 2211 2212 2213 2214 2221 2222 2223 2224 2231 2232 2233 2234 2241 2242 2243 2244 2311 2312 2313 2314 2321 2322 2323 2324 2331 2332 2333 2334 2341 2342 2343 2344 2411 2412 2413 2414 2421 2422 2423 2424 2431 2432 2433 2434 2441 2442 2443 2444 E 3 112 0 0 E 3 114 0 0 E 3 122 0 0 E 3 124 0 0 E 3 132 0 0 E 3 134 1 1 0 0 E 3 142 0 0 E 3 144 0 0 E 3 2 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 E 3 3111 3112 3113 3114 3121 3122 3123 3124 3131 3132 3133 3134 3141 3142 3143 3144 3211 3212 3213 3214 3221 3222 3223 3224 3231 3232 3233 3234 3241 3242 3243 3244 3311 3312 3313 3314 3321 3322 3323 3324 3331 3332 3333 3334 3341 3342 3343 3344 3411 3412 3413 3414 3421 3422 3423 3424 3431 3432 3433 3434 3441 3442 3443 3444 3 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 k List. E 2 hj, E 3 hjk=Ek&M’j. h=1 j=3 List. E 213={4} k=4 E 3134=E 4&M’ 3 k List. E 3 hij, E 4 hijk = Ek & M’j & M’i 3 Level, Stride=4 p. Trees for paths of len=2 (2 edges and 3 vertices (unique except for endpts) ) Level=2 E 3 key E 1 1111 0 1112 0 1113 0 1114 0 1121 0 1122 0 1123 0 1124 0 1131 0 1132 0 1133 0 1134 0 1141 0 1142 0 1143 0 1144 0 1211 0 1212 0 1213 0 1214 0 1221 0 1222 0 1223 0 1224 0 1231 0 1232 0 1233 0 1234 0 1241 0 1242 0 1243 0 1244 0 1311 0 1312 0 1313 0 1314 0 1321 0 1322 0 1323 0 1324 0 1331 0 1332 0 1333 0 1334 0 1341 1 1342 1 1343 0 1344 0 1411 0 1412 0 1413 0 1414 0 1421 0 1422 0 1423 0 1424 0 1431 1 1432 0 1433 0 1434 0 1441 0 1442 0 1443 0 1444 0 List. E 3134={1, 2} h=1 i=3 j=4 k=2 Level=3 (So E 2 is the upper 3 levels of E 3) 1 1 Level=2 (These are exactly the Level=1 of E) L 23 1 0 0 1 1 L 23 2 0 0 0 1 L 23 3 1 0 0 1 L 23 4 1 0 L 13 14 0 0 1 0 L 13 24 1 0 E 3 134 1 1 0 0 E 3 143 1 0 0 0 E 3 241 0 0 1 0 L 13 31 0 0 0 1 L 13 34 1 0 0 0 L 13 41 0 0 1 0 L 13 43 1 0 0 0 Level=0 (We just computed these) E 3 243 1 0 0 0 List. E 3241={3} h=2 i=4 j=1 k=3 List. E 3243={1} h=2 i=4 j=3 k=1 Level=1 (These are exactly the Level=0’s of E 2) L 13 13 0 0 0 1 E 3 E 3 M’ 4 143 4 1 1 1 0 00 00 h=1 j=4 k=3 0 0 1 0 00 00 E 3143=E 3&M’ 4 0 0 1 0 00 00 0 1 0 0 00 00 E 3 0 00 00 E 2 M’ 4 142 0 00 00 h=1 j=4 k=2 0 0 1 0 00 00 00 E 3142=E 2&M’ 4 0 1 0 0 1 1 00 01 0 pure 0 1 0 0 00 00 10 0 00 00 h=2 j=4 List. E 224={1, 3} k=1 0 00 00 E 3241=E 1&M’ 4 241 E 1 M’ 4 0 00 00 0 0 1 0 00 00 1 1 1 0 00 00 0 1 0 0 00 00 E 3 0 00 00 h=2 j=4 k=3 243 0 00 0 0 E 3 M’ 4 0 00 00 3 1 1 1 0 00 00 E 243=E 3&M’ 4 0 1 0 0 00 00 1 0 00 00 E 3 0 00 00 314 E 4 M’ 1 0 00 00 1 0 0 h=3 j=1 k=4 1 00 01 1 0 00 00 1 3314=E 4&M’ 1 1 1 0 00 00 0 1 E 0 0 00 00 E 3 0 00 00 E 1 M’ 4 341 0 00 00 0 0 1 0 00 00 h=3 j=4 k=1 0 0 10 00 1 1 1 0 10 00 E 3341=E 1&M’ 4 1 0 00 00 0 0 E 3 0 00 00 E 2 M’ 4 342 0 01 10 0 1 0 0 00 00 h=3 j=4 k=2 0 1 0 0 00 00 E 3342=E 2&M’ 4 1 0 0 00 00 0 11 00 00 E 3 0 00 00 E 3 M’ 1 413 0 00 00 h=4 j=1 k=3 1 0 00 0 0 1 0 00 00 E 3413=E 3&M’ 1 1 0 00 00 3 E E 3 E 4 M’ 3 134 E 1 M’ 3 431 1 0 0 1 h=4 j=3 k=1 1 0 0 1 E 3431=E 1&M’ 3 1 0 1 1 1 E 3 4111 4112 4113 4114 4121 4122 4123 4124 4131 4132 4133 4134 4141 4142 4143 4144 4211 4212 4213 4214 4221 4222 4223 4224 4231 4232 4233 4234 4241 4242 4243 4244 4311 4312 4313 4314 4321 4322 4323 4324 4331 4332 4333 4334 4341 4342 4343 4344 4411 4412 4413 4414 4421 4422 4423 4424 4431 4432 4433 4434 4441 4442 4443 4444 E 3 314 0 1 1 0 E 3 341 0 0 1 0 E 3 413 0 0 0 1 E 3 431 0 0 0 1 List. E 3314={2, 3} h=3 i=1 j=4 k=2 E 2 0 0 0 1 E 3 0 0 0 1 E 1 0 0 1 1 E 2 0 0 0 1 M’ 3 1 1 0 1 M’ 1 0 1 1 1 M’ 4 1 1 1 0 E 41342 0 0 0 List. E 3143={1} 0 42413 E 0 0 E 42431 0 0 List. E 3341={3} 0 0 E 43142 0 List. E 3413={4} 0 0 List. E 3431={4} 0 No 5 vertex (4 edge) paths. Creation stops. The Stride=|V|, Levels=Diam Path Mask is: E E 2 E 3 : Edlongest_path
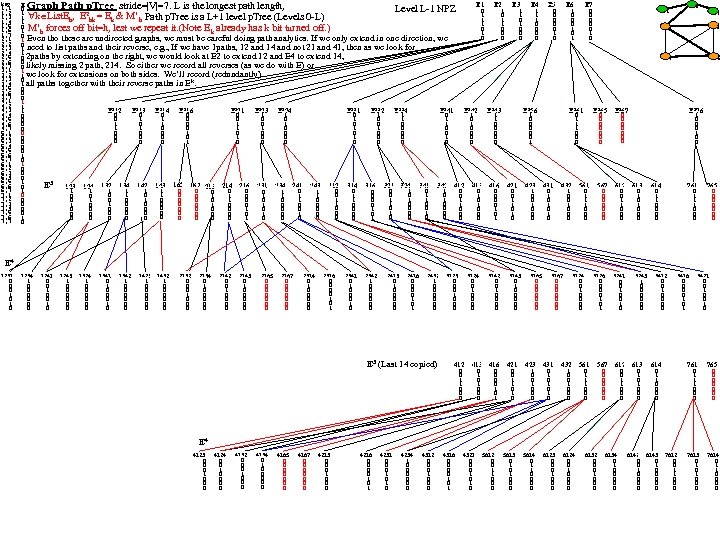 key 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 Graph Path p. Tree stride=|V|=7. L is the longest path length, E E 1 E 2 E 3 E 4 E 5 E 6 E 7 0 0 1 1 1 0 1 2 1 0 1 1 0 0 0 1 h hk k h 1 1 0 0 0 0 0 1 0 1 h k 1 0 0 0 1 0 1 Even tho these are undirected graphs, we must be careful doing path analytics. If we only extend in one direction, we 0 1 need to list paths and their reverse, e. g. , If we have 1 paths, 12 and 14 and not 21 and 41, then as we look for 1 0 2 paths by extending on the right, we would look at E 2 to extend 12 and E 4 to extend 14, 0 0 likely missing 2 path, 214. So either we record all reverses (as we do with E) or 1 1 we look for extensions on both sides. We’ll record (redundantly) 0 k 1 all paths together with their reverse paths in E. 0 0 0 1 1 1 E 212 E 213 E 214 E 216 E 221 E 223 E 224 E 231 E 232 E 234 E 256 E 241 E 242 E 243 E 261 E 265 0 0 0 1 1 1 0 0 0 0 1 0 1 0 1 0 0 0 1 1 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 E 3 124 132 134 142 143 165 167 213 214 216 231 234 241 243 312 314 316 321 324 341 342 413 416 421 423 431 432 561 567 0 1 0 1 1 1 0 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 0 0 0 0 1 1 0 0 0 0 1 1 0 1 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 Level L-1 NPZ k List. E , E = E & M’ Path p. Tree is a L+1 level p. Tree (Levels 0 -L) M’ forces off bit=h, lest we repeat it. (Note E already has k bit turned off. ) 6 5 7 1 2 4 3 E 267 E 276 0 0 0 0 1 0 0 612 613 0 0 1 1 0 0 0 614 761 0 1 1 0 0 0 1 1 1 0 0 0 765 0 0 0 0 E 4 1231 0 0 0 1 0 1234 1 0 0 0 1241 0 0 1 0 1243 1 0 0 0 1324 1 0 0 0 1341 0 0 0 1342 1 0 0 0 1423 1 0 0 0 1432 1 0 0 0 2132 0 0 0 1 0 0 0 2134 0 1 0 0 0 2142 0 0 1 0 0 2143 0 1 0 0 0 2165 0 0 0 0 2167 0 0 0 0 2314 0 1 0 0 0 2316 0 0 1 0 1 2341 0 0 0 1 0 2342 1 0 0 0 2413 0 1 0 0 0 2416 0 0 1 0 1 2432 1 0 0 0 E 3 (Last 14 copied) 3123 0 0 0 1 0 0 0 3124 0 0 1 0 0 412 0 0 1 1 0 0 0 3142 0 0 1 0 0 413 416 0 1 0 0 0 0 1 3143 0 1 0 0 0 421 0 0 1 1 0 3165 0 0 0 0 3167 0 0 0 0 423 431 1 0 0 0 0 1 0 1 0 3124 0 0 1 0 0 3126 0 0 1 0 1 432 561 1 0 0 0 0 1 1 1 0 0 0 3241 0 0 1 0 3243 1 0 0 0 567 612 613 0 0 0 0 0 1 1 0 0 0 3412 0 0 1 0 0 3416 0 0 1 0 1 614 3421 0 0 1 0 761 0 1 1 0 0 765 7613 0 1 0 0 0 7614 0 1 1 0 0 0 1 1 1 0 0 0 0 0 E 4 4123 0 0 0 1 0 0 0 4124 0 0 1 0 0 4132 0 0 0 1 0 0 0 4134 0 1 0 0 0 4165 0 0 0 0 4167 0 0 0 0 4213 0 0 0 1 0 0 0 4216 0 0 1 0 1 4231 0 0 0 1 0 4234 1 0 0 0 4312 0 0 0 1 0 0 0 4316 0 0 1 0 1 4321 0 0 0 1 0 5612 0 0 1 1 0 0 0 5613 0 1 0 0 0 5614 0 1 1 0 0 6123 0 0 0 1 0 0 0 6124 0 0 1 0 0 6132 0 0 0 1 0 0 0 6134 0 1 0 0 0 6142 6143 0 0 0 1 1 0 0 0 0 0 7612 0 0 1 1 0 0 0
key 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 Graph Path p. Tree stride=|V|=7. L is the longest path length, E E 1 E 2 E 3 E 4 E 5 E 6 E 7 0 0 1 1 1 0 1 2 1 0 1 1 0 0 0 1 h hk k h 1 1 0 0 0 0 0 1 0 1 h k 1 0 0 0 1 0 1 Even tho these are undirected graphs, we must be careful doing path analytics. If we only extend in one direction, we 0 1 need to list paths and their reverse, e. g. , If we have 1 paths, 12 and 14 and not 21 and 41, then as we look for 1 0 2 paths by extending on the right, we would look at E 2 to extend 12 and E 4 to extend 14, 0 0 likely missing 2 path, 214. So either we record all reverses (as we do with E) or 1 1 we look for extensions on both sides. We’ll record (redundantly) 0 k 1 all paths together with their reverse paths in E. 0 0 0 1 1 1 E 212 E 213 E 214 E 216 E 221 E 223 E 224 E 231 E 232 E 234 E 256 E 241 E 242 E 243 E 261 E 265 0 0 0 1 1 1 0 0 0 0 1 0 1 0 1 0 0 0 1 1 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 E 3 124 132 134 142 143 165 167 213 214 216 231 234 241 243 312 314 316 321 324 341 342 413 416 421 423 431 432 561 567 0 1 0 1 1 1 0 0 0 0 0 1 1 0 0 0 1 0 1 0 0 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 0 0 0 0 1 1 0 0 0 0 1 1 0 1 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 Level L-1 NPZ k List. E , E = E & M’ Path p. Tree is a L+1 level p. Tree (Levels 0 -L) M’ forces off bit=h, lest we repeat it. (Note E already has k bit turned off. ) 6 5 7 1 2 4 3 E 267 E 276 0 0 0 0 1 0 0 612 613 0 0 1 1 0 0 0 614 761 0 1 1 0 0 0 1 1 1 0 0 0 765 0 0 0 0 E 4 1231 0 0 0 1 0 1234 1 0 0 0 1241 0 0 1 0 1243 1 0 0 0 1324 1 0 0 0 1341 0 0 0 1342 1 0 0 0 1423 1 0 0 0 1432 1 0 0 0 2132 0 0 0 1 0 0 0 2134 0 1 0 0 0 2142 0 0 1 0 0 2143 0 1 0 0 0 2165 0 0 0 0 2167 0 0 0 0 2314 0 1 0 0 0 2316 0 0 1 0 1 2341 0 0 0 1 0 2342 1 0 0 0 2413 0 1 0 0 0 2416 0 0 1 0 1 2432 1 0 0 0 E 3 (Last 14 copied) 3123 0 0 0 1 0 0 0 3124 0 0 1 0 0 412 0 0 1 1 0 0 0 3142 0 0 1 0 0 413 416 0 1 0 0 0 0 1 3143 0 1 0 0 0 421 0 0 1 1 0 3165 0 0 0 0 3167 0 0 0 0 423 431 1 0 0 0 0 1 0 1 0 3124 0 0 1 0 0 3126 0 0 1 0 1 432 561 1 0 0 0 0 1 1 1 0 0 0 3241 0 0 1 0 3243 1 0 0 0 567 612 613 0 0 0 0 0 1 1 0 0 0 3412 0 0 1 0 0 3416 0 0 1 0 1 614 3421 0 0 1 0 761 0 1 1 0 0 765 7613 0 1 0 0 0 7614 0 1 1 0 0 0 1 1 1 0 0 0 0 0 E 4 4123 0 0 0 1 0 0 0 4124 0 0 1 0 0 4132 0 0 0 1 0 0 0 4134 0 1 0 0 0 4165 0 0 0 0 4167 0 0 0 0 4213 0 0 0 1 0 0 0 4216 0 0 1 0 1 4231 0 0 0 1 0 4234 1 0 0 0 4312 0 0 0 1 0 0 0 4316 0 0 1 0 1 4321 0 0 0 1 0 5612 0 0 1 1 0 0 0 5613 0 1 0 0 0 5614 0 1 1 0 0 6123 0 0 0 1 0 0 0 6124 0 0 1 0 0 6132 0 0 0 1 0 0 0 6134 0 1 0 0 0 6142 6143 0 0 0 1 1 0 0 0 0 0 7612 0 0 1 1 0 0 0
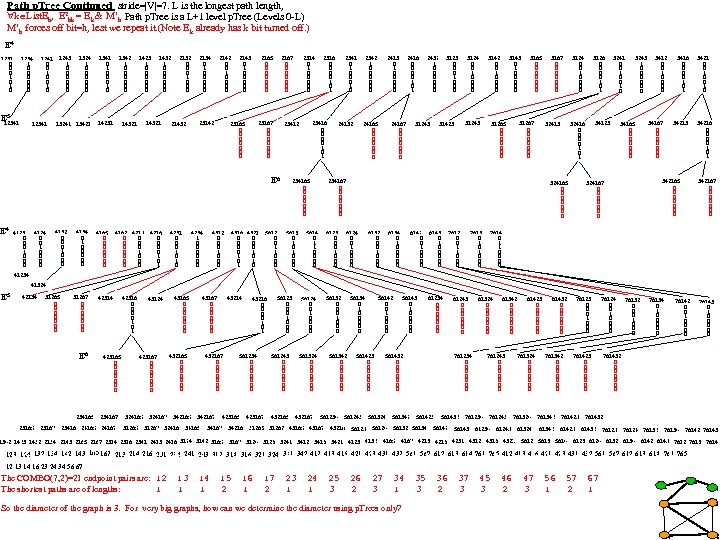 Path p. Tree Continued stride=|V|=7. L is the longest path length, k List. Eh, E 2 hk = Ek & M’h Path p. Tree is a L+1 level p. Tree (Levels 0 -L) M’h forces off bit=h, lest we repeat it. (Note E k already has k bit turned off. ) E 4 1231 0 0 0 1 0 1234 1 0 0 0 E 5 12341 1241 0 0 1 0 12341 1243 1 0 0 0 1324 1 0 0 0 1341 0 0 0 13241 1342 1 0 0 0 14231 1423 1 0 0 0 14321 2132 0 0 0 1 0 0 0 21432 2134 0 1 0 0 0 2142 0 0 1 0 0 23142 2143 0 1 0 0 0 2165 0 0 0 0 2167 0 0 0 0 23165 0 0 0 0 4123 0 0 0 1 0 0 0 4124 0 0 1 0 0 4132 0 0 0 1 0 0 0 4134 0 1 0 0 0 4165 0 0 0 0 4167 4213 0 0 0 0 1 0 0 0 4216 0 0 1 0 1 42316 0 0 1 0 1 43124 4231 0 0 0 1 0 4234 1 0 0 0 4312 0 0 0 1 0 0 0 4316 4321 0 0 0 0 1 1 0 5612 0 0 1 1 0 0 0 234165 0 0 0 0 5613 0 1 0 0 0 2316 0 0 1 0 1 2341 0 0 0 1 0 23416 0 0 1 0 1 23412 E 6 E 4 2314 0 1 0 0 0 5614 0 1 1 0 0 24132 2342 1 0 0 0 2413 0 1 0 0 0 2416 0 0 1 0 1 24167 0 0 0 0 24165 0 0 0 0 2432 1 0 0 0 31243 3123 0 0 0 1 0 0 0 3124 0 0 1 0 0 3142 0 0 1 0 0 31243 31423 3143 0 1 0 0 0 3165 0 0 0 0 31267 0 0 0 0 31265 0 0 0 0 3124 0 0 1 0 0 32413 234167 0 0 0 0 6123 0 0 0 1 0 0 0 3167 0 0 0 0 6132 0 0 0 1 0 0 0 6134 0 1 0 0 0 6142 6143 0 0 0 1 1 0 0 0 0 0 7612 0 0 1 1 0 0 0 7613 0 1 0 0 0 3241 0 0 1 0 34123 32416 0 0 1 0 1 324165 0 0 0 0 6124 0 0 1 0 0 3126 0 0 1 0 1 3243 1 0 0 0 34165 0 0 0 0 3412 0 0 1 0 0 3416 0 0 1 0 1 34167 0 0 0 0 3421 0 0 1 0 34213 34216 0 0 1 0 1 342165 0 0 0 0 324167 0 0 0 0 342167 0 0 0 0 7614 0 1 1 0 0 41234 41324 E 5 42134 31265 0 0 0 0 31267 0 0 0 0 E 6 234165 42314 423165 0 0 0 0 234167 23165 23167 23416 24165 24167 423167 0 0 0 0 432165 0 0 0 0 324165 324167 342165 31265 43167 0 0 0 0 43165 0 0 0 0 43214 432167 0 0 0 0 342167 31267 32416 34165 561234 0 0 0 0 423165 56124 0 0 1 0 0 561243 0 0 0 0 423167 34216 56123 0 0 0 1 0 0 0 43216 0 0 1 0 1 432165 561324 0 0 0 0 432167 56132 0 0 0 1 0 0 0 561342 0 0 0 0 561234 56142 0 0 1 0 0 56134 0 1 0 0 0 561423 0 0 0 0 561243 31265 31267 43165 43167 43216 56123 56143 0 1 0 0 0 61234 0 0 0 0 561432 0 0 0 0 561324 561342 61243 0 0 0 0 61324 0 0 0 0 761234 0 0 0 0 561423 561432 56124 56132 56134 56142 61342 0 0 0 0 761243 0 0 0 0 761234 761243 56143 61234 61423 0 0 0 0 761324 0 0 0 0 761342 0 0 0 0 761324 761342 61243 1342 1423 1432 2134 2143 2165 2167 2314 2316 2341 2413 2416 3124 3142 3165 3167 3124 3126 3241 3412 3416 3421 4123 4132 4165 4167 4213 4216 4231 4312 4316 4321 61324 76123 0 0 0 1 0 0 0 61432 0 0 0 0 61342 76124 0 0 1 0 0 761423 0 0 0 0 761423 76132 0 0 0 1 0 0 0 76134 0 1 0 0 0 76142 0 0 1 0 0 76143 0 1 0 0 0 761432 0 0 0 0 761432 76123 76124 76132 76134 76142 76143 5612 5613 5614 6123 6124 6132 6134 6142 6143 7612 7613 7614 123 124 132 134 142 143 165 167 213 214 216 231 234 241 243 312 314 316 321 324 341 342 413 416 421 423 431 432 561 567 612 613 614 761 765 412 413 416 421 423 431 432 561 567 612 613 614 761 765 12 13 14 16 23 24 34 56 67 The COMBO(7, 2)=21 endpoint pairs are: 12 The shortest paths are of lengths: 1 13 1 14 1 15 2 16 1 17 2 23 1 24 1 25 3 26 2 27 3 34 1 So the diameter of the graph is 3. For very big graphs, how can we determine the diameter using p. Trees only? 35 3 36 2 37 3 45 3 46 2 47 3 56 1 57 2 67 1 6 5 7 1 2 4 3
Path p. Tree Continued stride=|V|=7. L is the longest path length, k List. Eh, E 2 hk = Ek & M’h Path p. Tree is a L+1 level p. Tree (Levels 0 -L) M’h forces off bit=h, lest we repeat it. (Note E k already has k bit turned off. ) E 4 1231 0 0 0 1 0 1234 1 0 0 0 E 5 12341 1241 0 0 1 0 12341 1243 1 0 0 0 1324 1 0 0 0 1341 0 0 0 13241 1342 1 0 0 0 14231 1423 1 0 0 0 14321 2132 0 0 0 1 0 0 0 21432 2134 0 1 0 0 0 2142 0 0 1 0 0 23142 2143 0 1 0 0 0 2165 0 0 0 0 2167 0 0 0 0 23165 0 0 0 0 4123 0 0 0 1 0 0 0 4124 0 0 1 0 0 4132 0 0 0 1 0 0 0 4134 0 1 0 0 0 4165 0 0 0 0 4167 4213 0 0 0 0 1 0 0 0 4216 0 0 1 0 1 42316 0 0 1 0 1 43124 4231 0 0 0 1 0 4234 1 0 0 0 4312 0 0 0 1 0 0 0 4316 4321 0 0 0 0 1 1 0 5612 0 0 1 1 0 0 0 234165 0 0 0 0 5613 0 1 0 0 0 2316 0 0 1 0 1 2341 0 0 0 1 0 23416 0 0 1 0 1 23412 E 6 E 4 2314 0 1 0 0 0 5614 0 1 1 0 0 24132 2342 1 0 0 0 2413 0 1 0 0 0 2416 0 0 1 0 1 24167 0 0 0 0 24165 0 0 0 0 2432 1 0 0 0 31243 3123 0 0 0 1 0 0 0 3124 0 0 1 0 0 3142 0 0 1 0 0 31243 31423 3143 0 1 0 0 0 3165 0 0 0 0 31267 0 0 0 0 31265 0 0 0 0 3124 0 0 1 0 0 32413 234167 0 0 0 0 6123 0 0 0 1 0 0 0 3167 0 0 0 0 6132 0 0 0 1 0 0 0 6134 0 1 0 0 0 6142 6143 0 0 0 1 1 0 0 0 0 0 7612 0 0 1 1 0 0 0 7613 0 1 0 0 0 3241 0 0 1 0 34123 32416 0 0 1 0 1 324165 0 0 0 0 6124 0 0 1 0 0 3126 0 0 1 0 1 3243 1 0 0 0 34165 0 0 0 0 3412 0 0 1 0 0 3416 0 0 1 0 1 34167 0 0 0 0 3421 0 0 1 0 34213 34216 0 0 1 0 1 342165 0 0 0 0 324167 0 0 0 0 342167 0 0 0 0 7614 0 1 1 0 0 41234 41324 E 5 42134 31265 0 0 0 0 31267 0 0 0 0 E 6 234165 42314 423165 0 0 0 0 234167 23165 23167 23416 24165 24167 423167 0 0 0 0 432165 0 0 0 0 324165 324167 342165 31265 43167 0 0 0 0 43165 0 0 0 0 43214 432167 0 0 0 0 342167 31267 32416 34165 561234 0 0 0 0 423165 56124 0 0 1 0 0 561243 0 0 0 0 423167 34216 56123 0 0 0 1 0 0 0 43216 0 0 1 0 1 432165 561324 0 0 0 0 432167 56132 0 0 0 1 0 0 0 561342 0 0 0 0 561234 56142 0 0 1 0 0 56134 0 1 0 0 0 561423 0 0 0 0 561243 31265 31267 43165 43167 43216 56123 56143 0 1 0 0 0 61234 0 0 0 0 561432 0 0 0 0 561324 561342 61243 0 0 0 0 61324 0 0 0 0 761234 0 0 0 0 561423 561432 56124 56132 56134 56142 61342 0 0 0 0 761243 0 0 0 0 761234 761243 56143 61234 61423 0 0 0 0 761324 0 0 0 0 761342 0 0 0 0 761324 761342 61243 1342 1423 1432 2134 2143 2165 2167 2314 2316 2341 2413 2416 3124 3142 3165 3167 3124 3126 3241 3412 3416 3421 4123 4132 4165 4167 4213 4216 4231 4312 4316 4321 61324 76123 0 0 0 1 0 0 0 61432 0 0 0 0 61342 76124 0 0 1 0 0 761423 0 0 0 0 761423 76132 0 0 0 1 0 0 0 76134 0 1 0 0 0 76142 0 0 1 0 0 76143 0 1 0 0 0 761432 0 0 0 0 761432 76123 76124 76132 76134 76142 76143 5612 5613 5614 6123 6124 6132 6134 6142 6143 7612 7613 7614 123 124 132 134 142 143 165 167 213 214 216 231 234 241 243 312 314 316 321 324 341 342 413 416 421 423 431 432 561 567 612 613 614 761 765 412 413 416 421 423 431 432 561 567 612 613 614 761 765 12 13 14 16 23 24 34 56 67 The COMBO(7, 2)=21 endpoint pairs are: 12 The shortest paths are of lengths: 1 13 1 14 1 15 2 16 1 17 2 23 1 24 1 25 3 26 2 27 3 34 1 So the diameter of the graph is 3. For very big graphs, how can we determine the diameter using p. Trees only? 35 3 36 2 37 3 45 3 46 2 47 3 56 1 57 2 67 1 6 5 7 1 2 4 3
 E 2 E 1 0 0 1 1 E 1 The Path p. Tree 13 0 0 1 bit? Yes 0 1 Shortest. Path 1, 2 =132 E 3 E 2 0 0 0 1 14 0 1 1 0 134 1 1 0 0 143 1 0 0 0 142 0 0 E 3 1 0 0 1 24 1 0 1 bit? no 31 0 0 0 1 34 1 1 0 0 314 0 1 1 0 341 0 0 1 0 243 1 0 0 0 E 4 1 1 1 0 1 41 0 0 1 0 342 0 0 3 43 1 0 0 0 42 0 0 413 0 0 0 1 2 4 G 1 431 0 0 0 1 Diam. G 1 = maxk V(Diamk) = 2 How can we determine graph diameter? The Ek-diameter, diamk is the maximum of the minimum path lengths from k to the other vertices. For each k, proceed down from E k a level at a time and record the first occurrence of kh , h k. Diam 2=max{fo 21 fo 23 fo 24}=max{2 2 1}=2 Diam 1 = max{fo 12 fo 13 fo 14} = max{2 1 1} = 2 1 bit? No 1 2 0 0 1 1 0 0 0 Yes! SP 15 = 165 1 2 3 1 0 0 0 1 0 1 2 3 4 1 0 0 0 1 2 4 1 0 0 1 0 1 3 2 1 0 0 0 1 2 4 1 0 0 0 0 1 2 4 3 1 0 0 0 1 3 2 4 1 0 0 0 1 3 4 1 1 0 0 0 1 3 4 2 1 0 0 0 1 4 3 1 1 0 0 0 1 4 2 1 0 0 0 0 1 4 2 3 1 0 0 0 1 4 3 2 1 0 0 0 2 1 3 2 0 0 0 1 0 0 0 2 1 3 4 0 1 0 0 0 1 6 5 0 0 0 0 2 1 4 2 0 0 1 6 7 0 0 0 0 2 1 4 3 0 1 0 0 0 2 1 6 5 0 0 0 0 2 1 4 0 1 1 0 0 2 1 3 0 1 0 0 0 2 1 6 7 0 0 0 0 2 3 1 4 0 1 0 0 0 1 3 0 1 0 0 0 2 1 6 0 0 0 0 1 0 1 2 3 4 1 0 0 0 1 4 0 1 1 0 0 1 6 0 0 1 0 1 2 3 1 0 1 0 2 3 4 2 1 0 0 0 2 4 1 3 0 1 0 0 0 2 1 0 0 1 1 0 2 4 3 2 1 0 0 0 3 1 2 3 0 0 0 1 0 0 0 2 1 0 1 1 0 0 0 3 1 1 0 0 0 4 1 1 1 0 0 2 3 1 0 0 0 3 1 2 4 0 0 1 0 0 2 4 1 0 0 0 0 3 1 0 1 0 2 4 3 1 1 0 0 0 2 4 1 0 1 1 0 0 1 0 2 3 4 1 1 0 0 0 2 4 1 6 0 0 1 0 1 1 1 0 3 1 2 0 0 1 1 0 0 0 5 0 0 0 1 0 3 1 4 0 1 1 0 0 3 1 4 2 0 0 1 0 0 3 1 4 3 0 1 0 0 0 3 1 6 5 0 0 0 0 3 2 1 0 0 0 3 1 2 4 0 0 1 0 0 7 0 0 0 1 0 4 1 0 1 1 0 0 1 0 3 2 1 0 0 1 1 0 3 1 6 0 0 1 0 1 3 1 6 7 0 0 0 0 6 1 0 0 0 1 3 4 1 1 0 0 0 3 1 2 6 0 0 1 0 1 3 2 4 1 0 0 1 0 Diam 4=max{fo 41 fo 42 fo 43}=max{111}=1 Diam 3=max{fo 31 fo 32 fo 34}=max{1 2 1}=2 4 2 1 0 1 0 0 0 0 3 2 4 3 1 0 0 0 1 bit? no 4 3 1 1 0 0 0 3 4 1 6 0 0 1 0 1 7 2 1 3 4 1 0 1 1 0 0 1 0 3 4 1 2 0 0 1 0 0 6 5 5 6 1 0 0 0 1 3 4 2 1 0 0 0 0 3 4 2 1 0 0 1 0 6 1 0 1 1 1 0 0 0 4 1 2 0 0 1 1 0 0 0 4 1 2 3 0 0 0 1 0 0 0 4 1 2 4 0 0 1 0 0 4 1 3 0 1 0 0 0 4 1 3 2 0 0 0 1 0 0 0 6 7 0 0 0 0 6 5 0 0 0 0 4 1 6 0 0 1 0 1 4 1 3 4 0 1 0 0 0 4 1 6 5 0 0 0 0 7 6 1 0 0 0 1 0 0 4 2 1 0 0 1 1 0 4 1 6 7 0 0 0 0 4 4 2 3 1 0 0 0 4 2 1 3 0 0 0 1 0 0 0 4 2 1 6 0 0 1 0 1 3 G 2 1 bit? no 4 3 1 0 1 0 4 2 3 1 0 0 0 1 0 4 3 2 1 0 0 0 4 2 3 4 1 0 0 0 4 3 1 2 0 0 0 1 0 0 0 5 6 1 0 1 1 1 0 0 0 4 3 1 6 0 0 1 0 1 4 3 2 1 0 0 0 1 0 5 6 7 0 0 0 0 5 6 1 2 0 0 1 1 0 0 0 5 6 1 3 0 1 0 0 0 6 1 2 0 0 1 1 0 0 0 5 6 1 4 0 1 1 0 0 6 1 3 0 1 0 0 0 6 1 2 3 0 0 0 1 0 0 0 6 1 2 4 0 0 1 0 0 6 1 4 0 1 1 0 0 6 1 3 2 0 0 0 1 0 0 0 7 7 6 6 1 5 0 0 1 y 0 1 0 0 0 0 6 1 3 4 0 1 0 0 0 Diam 1=max{fo 12 13 14 15 16 17}=max{111212}=2 Diam 2=max{fo 21 23 24 25 26 27}=max{111333}=3 Diam 5=max{fo 51 52 53 54 56 57}=max{233312}=3 6 1 4 3 0 1 0 0 0 7 6 1 2 0 0 1 1 0 0 0 7 6 1 3 0 1 0 0 0 7 6 1 4 0 1 1 0 0 Diam 3=max{fo 31 32 34 35 36 37}=max{111323}=3 Diam 4=max{fo 41 42 43 45 46 47}=max{111323}=3 6 1 4 2 0 0 1 0 0 SP 72 =7612 Diam 6=max{fo 61 62 63 64 65 67}=max{122211}=2 Diam 7=max{fo 71 72 73 74 75 76}=max{233321}=3 Find the shortest path from Vk to Vh: Go down from Ek until you first encounter h. For G 1, shortest path from 1 to 2? Diam. G 2 = maxk V(Diamk) = 3 For G 2, shortest path from 7 to 2? from 1 to 5?
E 2 E 1 0 0 1 1 E 1 The Path p. Tree 13 0 0 1 bit? Yes 0 1 Shortest. Path 1, 2 =132 E 3 E 2 0 0 0 1 14 0 1 1 0 134 1 1 0 0 143 1 0 0 0 142 0 0 E 3 1 0 0 1 24 1 0 1 bit? no 31 0 0 0 1 34 1 1 0 0 314 0 1 1 0 341 0 0 1 0 243 1 0 0 0 E 4 1 1 1 0 1 41 0 0 1 0 342 0 0 3 43 1 0 0 0 42 0 0 413 0 0 0 1 2 4 G 1 431 0 0 0 1 Diam. G 1 = maxk V(Diamk) = 2 How can we determine graph diameter? The Ek-diameter, diamk is the maximum of the minimum path lengths from k to the other vertices. For each k, proceed down from E k a level at a time and record the first occurrence of kh , h k. Diam 2=max{fo 21 fo 23 fo 24}=max{2 2 1}=2 Diam 1 = max{fo 12 fo 13 fo 14} = max{2 1 1} = 2 1 bit? No 1 2 0 0 1 1 0 0 0 Yes! SP 15 = 165 1 2 3 1 0 0 0 1 0 1 2 3 4 1 0 0 0 1 2 4 1 0 0 1 0 1 3 2 1 0 0 0 1 2 4 1 0 0 0 0 1 2 4 3 1 0 0 0 1 3 2 4 1 0 0 0 1 3 4 1 1 0 0 0 1 3 4 2 1 0 0 0 1 4 3 1 1 0 0 0 1 4 2 1 0 0 0 0 1 4 2 3 1 0 0 0 1 4 3 2 1 0 0 0 2 1 3 2 0 0 0 1 0 0 0 2 1 3 4 0 1 0 0 0 1 6 5 0 0 0 0 2 1 4 2 0 0 1 6 7 0 0 0 0 2 1 4 3 0 1 0 0 0 2 1 6 5 0 0 0 0 2 1 4 0 1 1 0 0 2 1 3 0 1 0 0 0 2 1 6 7 0 0 0 0 2 3 1 4 0 1 0 0 0 1 3 0 1 0 0 0 2 1 6 0 0 0 0 1 0 1 2 3 4 1 0 0 0 1 4 0 1 1 0 0 1 6 0 0 1 0 1 2 3 1 0 1 0 2 3 4 2 1 0 0 0 2 4 1 3 0 1 0 0 0 2 1 0 0 1 1 0 2 4 3 2 1 0 0 0 3 1 2 3 0 0 0 1 0 0 0 2 1 0 1 1 0 0 0 3 1 1 0 0 0 4 1 1 1 0 0 2 3 1 0 0 0 3 1 2 4 0 0 1 0 0 2 4 1 0 0 0 0 3 1 0 1 0 2 4 3 1 1 0 0 0 2 4 1 0 1 1 0 0 1 0 2 3 4 1 1 0 0 0 2 4 1 6 0 0 1 0 1 1 1 0 3 1 2 0 0 1 1 0 0 0 5 0 0 0 1 0 3 1 4 0 1 1 0 0 3 1 4 2 0 0 1 0 0 3 1 4 3 0 1 0 0 0 3 1 6 5 0 0 0 0 3 2 1 0 0 0 3 1 2 4 0 0 1 0 0 7 0 0 0 1 0 4 1 0 1 1 0 0 1 0 3 2 1 0 0 1 1 0 3 1 6 0 0 1 0 1 3 1 6 7 0 0 0 0 6 1 0 0 0 1 3 4 1 1 0 0 0 3 1 2 6 0 0 1 0 1 3 2 4 1 0 0 1 0 Diam 4=max{fo 41 fo 42 fo 43}=max{111}=1 Diam 3=max{fo 31 fo 32 fo 34}=max{1 2 1}=2 4 2 1 0 1 0 0 0 0 3 2 4 3 1 0 0 0 1 bit? no 4 3 1 1 0 0 0 3 4 1 6 0 0 1 0 1 7 2 1 3 4 1 0 1 1 0 0 1 0 3 4 1 2 0 0 1 0 0 6 5 5 6 1 0 0 0 1 3 4 2 1 0 0 0 0 3 4 2 1 0 0 1 0 6 1 0 1 1 1 0 0 0 4 1 2 0 0 1 1 0 0 0 4 1 2 3 0 0 0 1 0 0 0 4 1 2 4 0 0 1 0 0 4 1 3 0 1 0 0 0 4 1 3 2 0 0 0 1 0 0 0 6 7 0 0 0 0 6 5 0 0 0 0 4 1 6 0 0 1 0 1 4 1 3 4 0 1 0 0 0 4 1 6 5 0 0 0 0 7 6 1 0 0 0 1 0 0 4 2 1 0 0 1 1 0 4 1 6 7 0 0 0 0 4 4 2 3 1 0 0 0 4 2 1 3 0 0 0 1 0 0 0 4 2 1 6 0 0 1 0 1 3 G 2 1 bit? no 4 3 1 0 1 0 4 2 3 1 0 0 0 1 0 4 3 2 1 0 0 0 4 2 3 4 1 0 0 0 4 3 1 2 0 0 0 1 0 0 0 5 6 1 0 1 1 1 0 0 0 4 3 1 6 0 0 1 0 1 4 3 2 1 0 0 0 1 0 5 6 7 0 0 0 0 5 6 1 2 0 0 1 1 0 0 0 5 6 1 3 0 1 0 0 0 6 1 2 0 0 1 1 0 0 0 5 6 1 4 0 1 1 0 0 6 1 3 0 1 0 0 0 6 1 2 3 0 0 0 1 0 0 0 6 1 2 4 0 0 1 0 0 6 1 4 0 1 1 0 0 6 1 3 2 0 0 0 1 0 0 0 7 7 6 6 1 5 0 0 1 y 0 1 0 0 0 0 6 1 3 4 0 1 0 0 0 Diam 1=max{fo 12 13 14 15 16 17}=max{111212}=2 Diam 2=max{fo 21 23 24 25 26 27}=max{111333}=3 Diam 5=max{fo 51 52 53 54 56 57}=max{233312}=3 6 1 4 3 0 1 0 0 0 7 6 1 2 0 0 1 1 0 0 0 7 6 1 3 0 1 0 0 0 7 6 1 4 0 1 1 0 0 Diam 3=max{fo 31 32 34 35 36 37}=max{111323}=3 Diam 4=max{fo 41 42 43 45 46 47}=max{111323}=3 6 1 4 2 0 0 1 0 0 SP 72 =7612 Diam 6=max{fo 61 62 63 64 65 67}=max{122211}=2 Diam 7=max{fo 71 72 73 74 75 76}=max{233321}=3 Find the shortest path from Vk to Vh: Go down from Ek until you first encounter h. For G 1, shortest path from 1 to 2? Diam. G 2 = maxk V(Diamk) = 3 For G 2, shortest path from 7 to 2? from 1 to 5?
 Sub. Graph E 1 Path p. Trees E 2 E 3 E 1 0&1= 0 0 1 1 C 1 0 0 1 1 E 2 0 0 0 1 13 0 1 0 0 0 1 13 0 0 0 1 14 0 1 1 14 0 0 134 1 1 1 0 0 1 134 1 0 0 0 142 0 1 0 0 0 1 142 0 0 E 3 1 1 0 0 0 1 1 1 31 0 0 0 1 1 1 24 1 0 143 1 1 0 0 0 1 143 1 0 0 0 241 0 0 1 0 243 1 0 0 0 C 3 1 0 0 1 E 4 1 1 1 0 1 31 0 0 0 1 34 1 1 1 0 0 1 34 1 0 0 0 314 0 1 1 0 1 314 0 0 1 0 341 0 0 1 1 0 1 341 0 0 1 0 342 0 1 0 0 0 1 342 0 0 C 4 1 0 1 0 1 1 413 0 1 0 0 0 1 1 1 41 0 0 1 0 413 0 0 0 1 1 42 0 0 0 0 43 1 1 0 0 0 1 43 1 0 0 0 431 0 0 0 1 1 431 0 0 0 1 2 3 4 G 1 Sub. Graph C in orange PC= 1 0 1 1 To get the C Path p. Tree, just remove all C’ p. Trees (in this case just E 2) then AND each G p. Tree with P C. One can then remove the second bit of every resulting p. Tree to get a Path p. Tree for three Cvertices in standard form, but it is not necessary to do so. Instead we will think of vertex 2 as being there but with no incident edges. That is tantamount to using the full vertex set for all Sub. Graphs and just removing all incident edges to vertices not in C. An advantage of this second point of view for p. Tree analytics is that all p. Trees are the same depth and can operate on each oneanother. Diameter of C? The Ck-diameter, Cdiamk is the max of the min path lengths from k to the other Cvertices. For each k, proceed down from Ck a level at a time and record the first occurrence of kh , h k. CDiam 1=max{fo 13 fo 14}=max{11}=1 Diam 3=max{fo 31 fo 34}=max{11}=1 Diam 4=max{fo 41 fo 43}=max{11}=1 Diam. C = maxk V(Diamk) = 1 Assuming we always use pop-count to instantaneously compute the 1 -count as we AND, then C is a clique iff all C 1 -counts are |V C|-1. In fact one can mine out all cliques by just analyzing the level=1 counts. Note: If one creates the G Path p. Tree, lots of tasks become easy! E. g. , clique mining, shortest path mining, degree community mining, density community mining! What else? A k-plex is a maximal subgraph in which each vertex is adjacent to all other vertices of the subgraph except at most k of them. A k-core is a maximal subgraph in which each vertex is adjacent to at least k other vertices of the subgraph. In any graph there is a whole hierarchy of cores of different order. k-plex existence alg (using the GPp. T): C is a k-plex iff v C|Cv| |VC|2–k 2 k-plex inheritance thm: Every induced subgraph of a k-plex is a k-plex. Mine all max k-plexes: Use |Cv| v C. k-core inheritance thm: If a cover of G by induced k-cores, G is a k-core. Mine all max k-cores: Use |Cv| v C k-core existence alg (using the GPp. T): C is a k-core iff v C, |V | k C
Sub. Graph E 1 Path p. Trees E 2 E 3 E 1 0&1= 0 0 1 1 C 1 0 0 1 1 E 2 0 0 0 1 13 0 1 0 0 0 1 13 0 0 0 1 14 0 1 1 14 0 0 134 1 1 1 0 0 1 134 1 0 0 0 142 0 1 0 0 0 1 142 0 0 E 3 1 1 0 0 0 1 1 1 31 0 0 0 1 1 1 24 1 0 143 1 1 0 0 0 1 143 1 0 0 0 241 0 0 1 0 243 1 0 0 0 C 3 1 0 0 1 E 4 1 1 1 0 1 31 0 0 0 1 34 1 1 1 0 0 1 34 1 0 0 0 314 0 1 1 0 1 314 0 0 1 0 341 0 0 1 1 0 1 341 0 0 1 0 342 0 1 0 0 0 1 342 0 0 C 4 1 0 1 0 1 1 413 0 1 0 0 0 1 1 1 41 0 0 1 0 413 0 0 0 1 1 42 0 0 0 0 43 1 1 0 0 0 1 43 1 0 0 0 431 0 0 0 1 1 431 0 0 0 1 2 3 4 G 1 Sub. Graph C in orange PC= 1 0 1 1 To get the C Path p. Tree, just remove all C’ p. Trees (in this case just E 2) then AND each G p. Tree with P C. One can then remove the second bit of every resulting p. Tree to get a Path p. Tree for three Cvertices in standard form, but it is not necessary to do so. Instead we will think of vertex 2 as being there but with no incident edges. That is tantamount to using the full vertex set for all Sub. Graphs and just removing all incident edges to vertices not in C. An advantage of this second point of view for p. Tree analytics is that all p. Trees are the same depth and can operate on each oneanother. Diameter of C? The Ck-diameter, Cdiamk is the max of the min path lengths from k to the other Cvertices. For each k, proceed down from Ck a level at a time and record the first occurrence of kh , h k. CDiam 1=max{fo 13 fo 14}=max{11}=1 Diam 3=max{fo 31 fo 34}=max{11}=1 Diam 4=max{fo 41 fo 43}=max{11}=1 Diam. C = maxk V(Diamk) = 1 Assuming we always use pop-count to instantaneously compute the 1 -count as we AND, then C is a clique iff all C 1 -counts are |V C|-1. In fact one can mine out all cliques by just analyzing the level=1 counts. Note: If one creates the G Path p. Tree, lots of tasks become easy! E. g. , clique mining, shortest path mining, degree community mining, density community mining! What else? A k-plex is a maximal subgraph in which each vertex is adjacent to all other vertices of the subgraph except at most k of them. A k-core is a maximal subgraph in which each vertex is adjacent to at least k other vertices of the subgraph. In any graph there is a whole hierarchy of cores of different order. k-plex existence alg (using the GPp. T): C is a k-plex iff v C|Cv| |VC|2–k 2 k-plex inheritance thm: Every induced subgraph of a k-plex is a k-plex. Mine all max k-plexes: Use |Cv| v C. k-core inheritance thm: If a cover of G by induced k-cores, G is a k-core. Mine all max k-cores: Use |Cv| v C k-core existence alg (using the GPp. T): C is a k-core iff v C, |V | k C
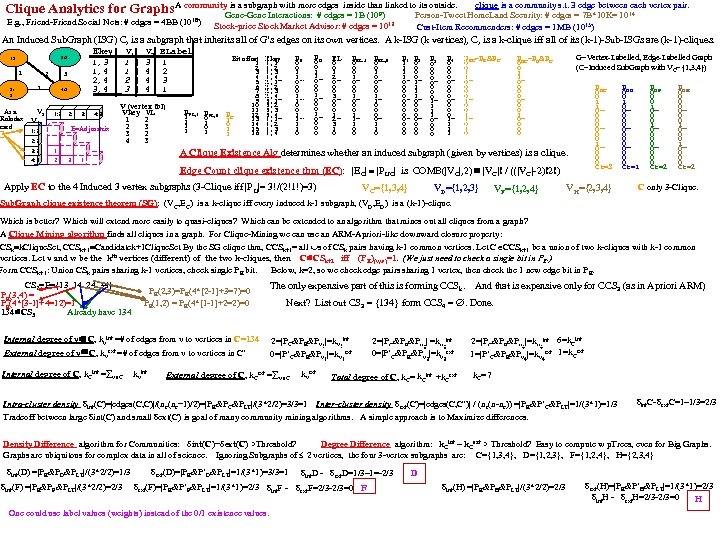 is a subgraph with more edges than its outside. clique is each Clique Analytics for Graphs A community. Gene-Gene Interactions: # edgesinside (109)linked to. Person-Tweet Home. Land a community s. t. =edge between 14 vertex pair. = 1 B Security: # edges 7 B*10 K= 10 E. g. , Friend-Friend Social Nets: # edges = 4 BB (1018) Stock-price Stock Market Advisor: # edges = 1013 Cust-Item Recommenders: # edges = 1 MB (1015) An Induced Sub. Graph (ISG) C, is a subgraph that inherits all of G’s edges on its own vertices. A k-ISG (k vertices), C, is a k-clique iff all of its (k-1)-Sub-ISGs are (k-1)-cliques. 1 3: 2 As a Rolodex card C Ekey 1, 3 1, 4 2, 4 3, 4 2: 3 12 2 3 1 V 2 V 1 4: 3 1: 2 2: 3 3: 2 4: 3 E=Adj matrix 1: 2 2: 3 3: 2 4: 3 V 1 1 | 2 | 3 | V 2 3 4 4 4 V (vertex tbl) Vkey VL 1 2 2 3 3 2 4 3 1 2 3 ELabel 1 2 3 1 PVL, 1 1 1 PVL, 0 0 1 Bit offset 1 2 3 4 5 6 7 8 9 10 11 12 PC 13 1 14 0 15 1 16 1 Ekey 1, 1 1, 2 1, 3 1, 4_ 2, 1 2, 2 2, 3 2, 4_ 3, 1 3, 2 3, 3 3, 4_ 4, 1 4, 2 4, 3 4, 4 PE 0 0 1 1_ 0 0 0 1_ 1 1 1 0 PU 0 0 1 1_ 0 0 0 1_ 0 0 EL 0 0 1 2_ 0 0 0 3_ 0 0 0 1_ 2 3 1 0 PEL. , 1 0 0 0 1_ 1 1 0 0 PEL. , 0 0 0 1 0_ 0 0 0 1_ 1 0 0 0_ 0 1 1 0 P 1 1 1_ 0 0 0 0_ 0 0 P 2 0 0_ 1 1_ 0 0 0 0 P 3 0 0 0 0_ 1 1_ 0 0 P 4 0 0 0 0_ 1 1 PEC=PE&PC 0 0 1 1_ 0 0_ 1 0 0 1_ 1 0 G=Vertex-Labelled, Edge-Labelled Graph (C=Induced Sub. Graph with VC={1, 3, 4}) PUC=PU&PC 0 0 1 1_ 0 0_ 0 0 0 1_ 0 0 A Clique Existence Alg determines whether an induced subgraph (given by vertices) is a clique. 1 Edge Count clique existence thm (EC): |EC| |PUC| is COMB(|VC|, 2) |VC|! / ((|VC|-2)!2!) Apply EC to the 4 Induced 3 vertex subgraphs (3 -Clique iff |P U|= 3!/(2!1!)=3) VC={1, 3, 4} VD={1, 2, 3} VF={1, 2, 4} PUC 0 0 1 1_ 0 0_ 0 0 0 1_ 0 0 Ct=3 VH={2, 3, 4} PUD 0 0 1 0_ 0 0 0 0_ 0 0 Ct=1 PUF 0 0 0 1_ 0 0_ 0 0 Ct=2 PUH 0 0_ 0 0 0 1_ 0 0 Ct=2 C only 3 -Clique. Sub. Graph clique existence theorem (SG): (VC, EC) is a k-clique iff every induced k-1 subgraph, (VD, ED) is a (k-1)-clique. Which is better? Which will extend more easily to quasi-cliques? Which can be extended to an algorithm that mines out all cliques from a graph? A Clique Mining algorithm finds all cliques in a graph. For Clique-Mining we can use an ARM-Apriori-like downward closure property: CSk k. Clique. Set, CCSk+1 Candidatek+1 Clique. Set By the SG clique thm, CCSk+1= all s of CSk pairs having k-1 common vertices. Let C CCSk+1 be a union of two k-cliques with k-1 common vertices. Let v and w be the kth vertices (different) of the two k-cliques, then C CSk+1 iff (PE)(v, w)=1. (We just need to check a single bit in PE. ) Form CCSk+1: Union CSk pairs sharing k-1 vertices, check single PE bit. Below, k=2, so we check edge pairs sharing 1 vertex, then check the 1 new edge bit in P E. CS 2=E={13 14 24 34} PE(3, 4) = PE(4*[3 -1]+4=12)=1 134 CS 3 Already have 134 PE(2, 3)=PE(4*[2 -1]+3=7)=0 PE(1, 2) = PE(4*[1 -1]+2=2)=0 Internal degree of v∈C, kvint =# of edges from v to vertices in C=134 External degree of v∈C, kvext =# of edges from v to vertices in C’ Internal degree of C, k. Cint = v C kvint The only expensive part of this is forming CCSk. And that is expensive only for CCS 3 (as in Apriori ARM) Next? List out CS 3 = {134} form CCS 4 = . Done. 2=|PC&PE&Pv 1|=kv 1 int 0=|P’C&PE&Pv 1|=kv 1 ext External degree of C, k. Cext = v C kvext 2=|PC&PE&Pv 3| =kv 3 int 0=|P’C&PE&Pv 3|=kv 3 ext Total degree of C, k. C= k. Cint +k. Cext 2=|PC&PE&Pv 4|=kv 4 int 6=k. Cint 1=|P’C&PE&Pv 4|=kv 4 ext 1=k. Cext k. C=7 Intra-cluster density δint(C)=|edges(C, C)|/(nc(nc− 1)/2)=|PE&PC&PLT|/(3*2/2)=3/3=1 Inter-cluster density δext(C)=|edges(C, C’)| / (nc(n-nc)) =|PE&P’C&PLT|=1/(3*1)=1/3 δint. C- δext. C=1– 1/3=2/3 Tradeoff between large δint(C) and small δext(C) is goal of many community mining algorithms. A simple approach is to Maximize differences. Density Difference algorithm for Communities: δint(C)−δext(C) >Threshold? Degree Difference algorithm: k. Cint – k. Cext > Threshold? Easy to compute w p. Trees, even for Big Graphs are ubiquitous for complex data in all of science. Ignoring Subgraphs of 2 vertices, the four 3 -vertex subgraphs are: C={1, 3, 4}, D={1, 2, 3}, F={1, 2, 4}, H={2, 3, 4} δint(D) =|PE&PD&PLT|/(3*2/2)=1/3 δint(F) =|PE&PF&PLT|/(3*2/2)=2/3 δext(D)=|PE&P’D&PLT|=1/(3*1)=3/3=1 δint. D - δext. D=1/3– 1=-2/3 δext(F)=|PE&P’F&PLT|=1/(3*1)=2/3 δint. F - δext. F=2/3 -2/3=0 F One could use label values (weights) instead of the 0/1 existence values. D δint(H) =|PE&PH&PLT|/(3*2/2)=2/3 δext(H)=|PE&P’H&PLT|=1/(3*1)=2/3 δint. H - δext. H=2/3 -2/3=0 H
is a subgraph with more edges than its outside. clique is each Clique Analytics for Graphs A community. Gene-Gene Interactions: # edgesinside (109)linked to. Person-Tweet Home. Land a community s. t. =edge between 14 vertex pair. = 1 B Security: # edges 7 B*10 K= 10 E. g. , Friend-Friend Social Nets: # edges = 4 BB (1018) Stock-price Stock Market Advisor: # edges = 1013 Cust-Item Recommenders: # edges = 1 MB (1015) An Induced Sub. Graph (ISG) C, is a subgraph that inherits all of G’s edges on its own vertices. A k-ISG (k vertices), C, is a k-clique iff all of its (k-1)-Sub-ISGs are (k-1)-cliques. 1 3: 2 As a Rolodex card C Ekey 1, 3 1, 4 2, 4 3, 4 2: 3 12 2 3 1 V 2 V 1 4: 3 1: 2 2: 3 3: 2 4: 3 E=Adj matrix 1: 2 2: 3 3: 2 4: 3 V 1 1 | 2 | 3 | V 2 3 4 4 4 V (vertex tbl) Vkey VL 1 2 2 3 3 2 4 3 1 2 3 ELabel 1 2 3 1 PVL, 1 1 1 PVL, 0 0 1 Bit offset 1 2 3 4 5 6 7 8 9 10 11 12 PC 13 1 14 0 15 1 16 1 Ekey 1, 1 1, 2 1, 3 1, 4_ 2, 1 2, 2 2, 3 2, 4_ 3, 1 3, 2 3, 3 3, 4_ 4, 1 4, 2 4, 3 4, 4 PE 0 0 1 1_ 0 0 0 1_ 1 1 1 0 PU 0 0 1 1_ 0 0 0 1_ 0 0 EL 0 0 1 2_ 0 0 0 3_ 0 0 0 1_ 2 3 1 0 PEL. , 1 0 0 0 1_ 1 1 0 0 PEL. , 0 0 0 1 0_ 0 0 0 1_ 1 0 0 0_ 0 1 1 0 P 1 1 1_ 0 0 0 0_ 0 0 P 2 0 0_ 1 1_ 0 0 0 0 P 3 0 0 0 0_ 1 1_ 0 0 P 4 0 0 0 0_ 1 1 PEC=PE&PC 0 0 1 1_ 0 0_ 1 0 0 1_ 1 0 G=Vertex-Labelled, Edge-Labelled Graph (C=Induced Sub. Graph with VC={1, 3, 4}) PUC=PU&PC 0 0 1 1_ 0 0_ 0 0 0 1_ 0 0 A Clique Existence Alg determines whether an induced subgraph (given by vertices) is a clique. 1 Edge Count clique existence thm (EC): |EC| |PUC| is COMB(|VC|, 2) |VC|! / ((|VC|-2)!2!) Apply EC to the 4 Induced 3 vertex subgraphs (3 -Clique iff |P U|= 3!/(2!1!)=3) VC={1, 3, 4} VD={1, 2, 3} VF={1, 2, 4} PUC 0 0 1 1_ 0 0_ 0 0 0 1_ 0 0 Ct=3 VH={2, 3, 4} PUD 0 0 1 0_ 0 0 0 0_ 0 0 Ct=1 PUF 0 0 0 1_ 0 0_ 0 0 Ct=2 PUH 0 0_ 0 0 0 1_ 0 0 Ct=2 C only 3 -Clique. Sub. Graph clique existence theorem (SG): (VC, EC) is a k-clique iff every induced k-1 subgraph, (VD, ED) is a (k-1)-clique. Which is better? Which will extend more easily to quasi-cliques? Which can be extended to an algorithm that mines out all cliques from a graph? A Clique Mining algorithm finds all cliques in a graph. For Clique-Mining we can use an ARM-Apriori-like downward closure property: CSk k. Clique. Set, CCSk+1 Candidatek+1 Clique. Set By the SG clique thm, CCSk+1= all s of CSk pairs having k-1 common vertices. Let C CCSk+1 be a union of two k-cliques with k-1 common vertices. Let v and w be the kth vertices (different) of the two k-cliques, then C CSk+1 iff (PE)(v, w)=1. (We just need to check a single bit in PE. ) Form CCSk+1: Union CSk pairs sharing k-1 vertices, check single PE bit. Below, k=2, so we check edge pairs sharing 1 vertex, then check the 1 new edge bit in P E. CS 2=E={13 14 24 34} PE(3, 4) = PE(4*[3 -1]+4=12)=1 134 CS 3 Already have 134 PE(2, 3)=PE(4*[2 -1]+3=7)=0 PE(1, 2) = PE(4*[1 -1]+2=2)=0 Internal degree of v∈C, kvint =# of edges from v to vertices in C=134 External degree of v∈C, kvext =# of edges from v to vertices in C’ Internal degree of C, k. Cint = v C kvint The only expensive part of this is forming CCSk. And that is expensive only for CCS 3 (as in Apriori ARM) Next? List out CS 3 = {134} form CCS 4 = . Done. 2=|PC&PE&Pv 1|=kv 1 int 0=|P’C&PE&Pv 1|=kv 1 ext External degree of C, k. Cext = v C kvext 2=|PC&PE&Pv 3| =kv 3 int 0=|P’C&PE&Pv 3|=kv 3 ext Total degree of C, k. C= k. Cint +k. Cext 2=|PC&PE&Pv 4|=kv 4 int 6=k. Cint 1=|P’C&PE&Pv 4|=kv 4 ext 1=k. Cext k. C=7 Intra-cluster density δint(C)=|edges(C, C)|/(nc(nc− 1)/2)=|PE&PC&PLT|/(3*2/2)=3/3=1 Inter-cluster density δext(C)=|edges(C, C’)| / (nc(n-nc)) =|PE&P’C&PLT|=1/(3*1)=1/3 δint. C- δext. C=1– 1/3=2/3 Tradeoff between large δint(C) and small δext(C) is goal of many community mining algorithms. A simple approach is to Maximize differences. Density Difference algorithm for Communities: δint(C)−δext(C) >Threshold? Degree Difference algorithm: k. Cint – k. Cext > Threshold? Easy to compute w p. Trees, even for Big Graphs are ubiquitous for complex data in all of science. Ignoring Subgraphs of 2 vertices, the four 3 -vertex subgraphs are: C={1, 3, 4}, D={1, 2, 3}, F={1, 2, 4}, H={2, 3, 4} δint(D) =|PE&PD&PLT|/(3*2/2)=1/3 δint(F) =|PE&PF&PLT|/(3*2/2)=2/3 δext(D)=|PE&P’D&PLT|=1/(3*1)=3/3=1 δint. D - δext. D=1/3– 1=-2/3 δext(F)=|PE&P’F&PLT|=1/(3*1)=2/3 δint. F - δext. F=2/3 -2/3=0 F One could use label values (weights) instead of the 0/1 existence values. D δint(H) =|PE&PH&PLT|/(3*2/2)=2/3 δext(H)=|PE&P’H&PLT|=1/(3*1)=2/3 δint. H - δext. H=2/3 -2/3=0 H
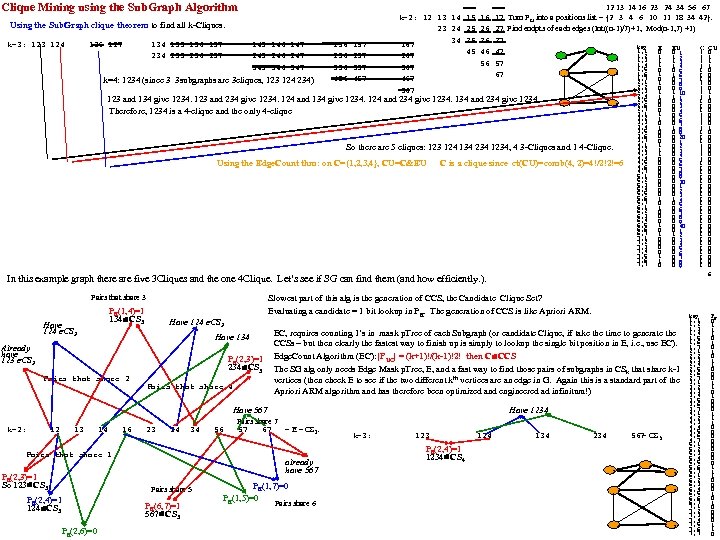 Clique Mining using the Sub. Graph Algorithm Using the Sub. Graph clique theorem to find all k-Cliques. k=3: 123 124 126 127 134 135 136 137 234 235 236 237 145 146 147 245 246 247 345 346 347 k=4: 1234 (since 3 3 subgraphs are 3 cliques, 123 124 234) 156 256 356 456 157 257 357 457 k=2: 12 13 14 15 23 24 25 34 35 167 45 267 367 467 567 16 26 36 46 56 12 13 14 16 23 24 34 56 67 17 Turn PU into a positions list = {2 3 4 6 10 11 18 34 42}. 27. Find endpts of each edges (Int((n-1)/7)+1, Mod(n-1, 7) +1) 37 key E EU C CU 1, 1 47 0 6 0 1 1 0 1, 2 1 5 1 2 1 1 7 1, 3 1 1 57 1, 4 1 1 1, 5 0 0 2 1, 6 1 1 1 6 0 0 67 1, 7 0 0 123 and 134 give 1234. 123 and 234 give 1234. 124 and 134 give 1234. 124 and 234 give 1234. 134 and 234 give 1234. Therefore, 1234 is a 4 -clique and the only 4 -clique 4 3 So there are 5 cliques: 123 124 134 234 1234, 4 3 -Cliques and 1 4 -Clique. Using the Edge. Count thm: on C={1, 2, 3, 4}, CU=C&EU C is a clique since ct(CU)=comb(4, 2)=4!/2!2!=6 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 1 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 7 8 9 10 1 2 3 4 5 6 7 8 9 20 1 2 3 4 5 6 7 8 9 30 1 2 3 4 5 6 7 8 9 40 1 2 3 4 5 6 7 8 9 1 1 1 1 0 0 0 0 0 0 0 0 In this example graph there are five 3 Cliques and the one 4 Clique. Let’s see if SG can find them (and how efficiently. ). Pairs that share 3 PE(1, 4)=1 134 CS 3 Have 124 CS 3 Slowest part of this alg is the generation of CCS, the Candidate Clique Set? Evaluating a candidate = 1 bit lookup in PE. The generation of CCS is like Apriori ARM. Have 124 CS 3 Have 134 Already have 123 CS 3 PE(2, 3)=1 234 CS 3 Pairs that share 2 Pairs that share 4 EC, requires counting 1’s in mask p. Tree of each Subgraph (or candidate Clique, if take the time to generate the CCSs – but then clearly the fastest way to finish up is simply to lookup the single bit position in E, i. e. , use EC). Edge. Count Algorithm (EC): |PUC| = (k+1)!/(k-1)!2! then C CCS The SG alg only needs Edge Mask p. Tree, E, and a fast way to find those pairs of subgraphs in CS k that share k-1 vertices (then check E to see if the two different kth vertices are an edge in G. Again this is a standard part of the Apriori ARM algorithm and has therefore been optimized and engineered ad infinitum!) Have 567 k=2: 12 13 14 16 23 24 34 Pairs that share 1 PE(2, 3)=1 So 123 CS 3 already have 567 Pairs share 5 PE(2, 4)=1 124 CS 3 PE(2, 6)=0 56 Have 1234 Pairs share 7 57 67 = E = CS 2. PE(6, 7)=1 567 CS 3 PE(1, 7)=0 PE(1, 5)=0 Pairs share 6 k=3: 123 124 134 567 CS 3. = 234 PE(2, 4)=1 1234 CS 4 6 5 7 1 2 4 3 key 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 0 0 1 1 0 0 0 0 0 0 0 0 0 0 6 PE 0 1 1 1 0 1 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 1 1 0 0 0 1 1 0
Clique Mining using the Sub. Graph Algorithm Using the Sub. Graph clique theorem to find all k-Cliques. k=3: 123 124 126 127 134 135 136 137 234 235 236 237 145 146 147 245 246 247 345 346 347 k=4: 1234 (since 3 3 subgraphs are 3 cliques, 123 124 234) 156 256 356 456 157 257 357 457 k=2: 12 13 14 15 23 24 25 34 35 167 45 267 367 467 567 16 26 36 46 56 12 13 14 16 23 24 34 56 67 17 Turn PU into a positions list = {2 3 4 6 10 11 18 34 42}. 27. Find endpts of each edges (Int((n-1)/7)+1, Mod(n-1, 7) +1) 37 key E EU C CU 1, 1 47 0 6 0 1 1 0 1, 2 1 5 1 2 1 1 7 1, 3 1 1 57 1, 4 1 1 1, 5 0 0 2 1, 6 1 1 1 6 0 0 67 1, 7 0 0 123 and 134 give 1234. 123 and 234 give 1234. 124 and 134 give 1234. 124 and 234 give 1234. 134 and 234 give 1234. Therefore, 1234 is a 4 -clique and the only 4 -clique 4 3 So there are 5 cliques: 123 124 134 234 1234, 4 3 -Cliques and 1 4 -Clique. Using the Edge. Count thm: on C={1, 2, 3, 4}, CU=C&EU C is a clique since ct(CU)=comb(4, 2)=4!/2!2!=6 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 1 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 7 8 9 10 1 2 3 4 5 6 7 8 9 20 1 2 3 4 5 6 7 8 9 30 1 2 3 4 5 6 7 8 9 40 1 2 3 4 5 6 7 8 9 1 1 1 1 0 0 0 0 0 0 0 0 In this example graph there are five 3 Cliques and the one 4 Clique. Let’s see if SG can find them (and how efficiently. ). Pairs that share 3 PE(1, 4)=1 134 CS 3 Have 124 CS 3 Slowest part of this alg is the generation of CCS, the Candidate Clique Set? Evaluating a candidate = 1 bit lookup in PE. The generation of CCS is like Apriori ARM. Have 124 CS 3 Have 134 Already have 123 CS 3 PE(2, 3)=1 234 CS 3 Pairs that share 2 Pairs that share 4 EC, requires counting 1’s in mask p. Tree of each Subgraph (or candidate Clique, if take the time to generate the CCSs – but then clearly the fastest way to finish up is simply to lookup the single bit position in E, i. e. , use EC). Edge. Count Algorithm (EC): |PUC| = (k+1)!/(k-1)!2! then C CCS The SG alg only needs Edge Mask p. Tree, E, and a fast way to find those pairs of subgraphs in CS k that share k-1 vertices (then check E to see if the two different kth vertices are an edge in G. Again this is a standard part of the Apriori ARM algorithm and has therefore been optimized and engineered ad infinitum!) Have 567 k=2: 12 13 14 16 23 24 34 Pairs that share 1 PE(2, 3)=1 So 123 CS 3 already have 567 Pairs share 5 PE(2, 4)=1 124 CS 3 PE(2, 6)=0 56 Have 1234 Pairs share 7 57 67 = E = CS 2. PE(6, 7)=1 567 CS 3 PE(1, 7)=0 PE(1, 5)=0 Pairs share 6 k=3: 123 124 134 567 CS 3. = 234 PE(2, 4)=1 1234 CS 4 6 5 7 1 2 4 3 key 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 0 0 1 1 0 0 0 0 0 0 0 0 0 0 6 PE 0 1 1 1 0 1 0 1 1 0 0 0 1 1 1 0 0 0 0 0 1 1 1 0 0 0 1 1 0
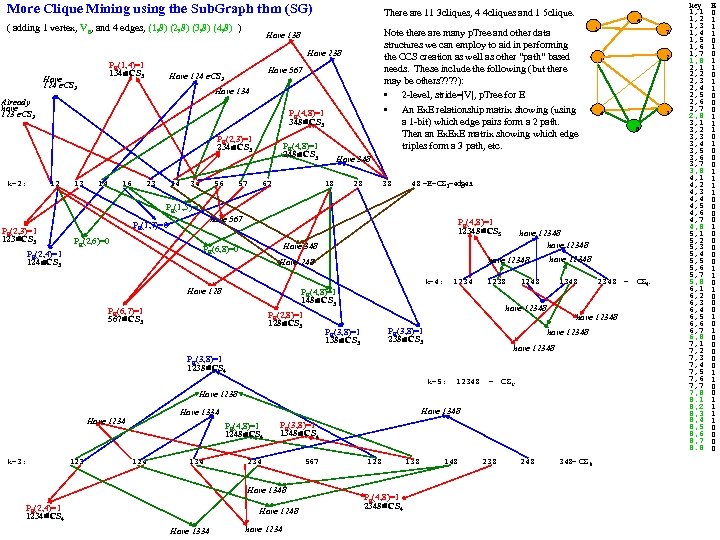 More Clique Mining using the Sub. Graph thm (SG) ( adding 1 vertex, V 8, and 4 edges, (1, 8) (2, 8) (3, 8) (4, 8) ) There are 11 3 cliques, 4 4 cliques and 1 5 clique. Note there are many p. Tree and other data structures we can employ to aid in performing the CCS creation as well as other “path” based needs. These include the following (but there may be others? ? ): • 2 -level, stride=|V|, p. Tree for E • An Ex. E relationship matrix showing (using a 1 -bit) which edge pairs form a 2 path. Then an Ex. E matrix showing which edge triples form a 3 path, etc. Have 138 Have 238 PE(1, 4)=1 134 CS 3 Have 124 CS 3 Have 567 Have 124 CS 3 Have 134 Already have 123 CS 3 PE(4, 8)=1 348 CS 3 PE(2, 3)=1 234 CS 3 k=2: 12 13 14 16 23 24 34 56 PE(4, 8)=1 248 CS 3 57 67 6 5 7 1 2 4 3 8 Have 348 18 28 38 48 =E=CS 2=edges. PE(1, 5)=0 PE(2, 3)=1 123 CS 3 have 567 PE(1, 7)=0 PE(2, 6)=0 PE(4, 8)=1 12348 CS 5 PE(2, 4)=1 124 CS 3 have 12348 Have 348 PE(6, 8)=0 k=4: Have 128 1234 1238 PE(4, 8)=1 148 CS 3 PE(6, 7)=1 567 CS 3 PE(2, 8)=1 128 CS 3 have 12348 Have 248 1348 have 12348 PE(3, 8)=1 238 CS 3 PE(3, 8)=1 138 CS 3 have 12348 PE(3, 8)=1 1238 CS 4 k=5: 12348 = CS 5. Have 1238 k=3: 123 Have 1348 Have 1334 Have 1234 PE(4, 8)=1 1248 CS 4 124 134 PE(3, 8)=1 1348 CS 4 234 567 Have 1348 PE(2, 4)=1 1234 CS 4 Have 1248 Have 1334 have 1234 128 PE(4, 8)=1 2348 CS 4 138 148 238 248 2348 = 348= CS 3. CS 4. key 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 2, 8 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 3, 8 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 4, 8 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 5, 8 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 6, 8 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 7, 8 8. 1 8, 2 8, 3 8, 4 8, 5 8, 6 8, 7 8. 8 E 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 1 1 0 1 0 0 0 0 0 1 1 1 1 0 0
More Clique Mining using the Sub. Graph thm (SG) ( adding 1 vertex, V 8, and 4 edges, (1, 8) (2, 8) (3, 8) (4, 8) ) There are 11 3 cliques, 4 4 cliques and 1 5 clique. Note there are many p. Tree and other data structures we can employ to aid in performing the CCS creation as well as other “path” based needs. These include the following (but there may be others? ? ): • 2 -level, stride=|V|, p. Tree for E • An Ex. E relationship matrix showing (using a 1 -bit) which edge pairs form a 2 path. Then an Ex. E matrix showing which edge triples form a 3 path, etc. Have 138 Have 238 PE(1, 4)=1 134 CS 3 Have 124 CS 3 Have 567 Have 124 CS 3 Have 134 Already have 123 CS 3 PE(4, 8)=1 348 CS 3 PE(2, 3)=1 234 CS 3 k=2: 12 13 14 16 23 24 34 56 PE(4, 8)=1 248 CS 3 57 67 6 5 7 1 2 4 3 8 Have 348 18 28 38 48 =E=CS 2=edges. PE(1, 5)=0 PE(2, 3)=1 123 CS 3 have 567 PE(1, 7)=0 PE(2, 6)=0 PE(4, 8)=1 12348 CS 5 PE(2, 4)=1 124 CS 3 have 12348 Have 348 PE(6, 8)=0 k=4: Have 128 1234 1238 PE(4, 8)=1 148 CS 3 PE(6, 7)=1 567 CS 3 PE(2, 8)=1 128 CS 3 have 12348 Have 248 1348 have 12348 PE(3, 8)=1 238 CS 3 PE(3, 8)=1 138 CS 3 have 12348 PE(3, 8)=1 1238 CS 4 k=5: 12348 = CS 5. Have 1238 k=3: 123 Have 1348 Have 1334 Have 1234 PE(4, 8)=1 1248 CS 4 124 134 PE(3, 8)=1 1348 CS 4 234 567 Have 1348 PE(2, 4)=1 1234 CS 4 Have 1248 Have 1334 have 1234 128 PE(4, 8)=1 2348 CS 4 138 148 238 248 2348 = 348= CS 3. CS 4. key 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 2, 8 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 3, 8 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 4, 8 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 5, 8 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 6, 8 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 7, 8 8. 1 8, 2 8, 3 8, 4 8, 5 8, 6 8, 7 8. 8 E 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 1 1 0 1 0 0 0 0 0 1 1 1 1 0 0
 Mining for Communities with more relaxed definitions than cliques (from Fortunatos survey) There are many cohesiveness definitions other than a Clique. Another criterion for subgraph cohesion relies idea that a vertex must be adjacent to some min # of other vertices. In social network analysis there are two complementary ways of expressing this. A k-plex is a maximal subgraph in which each vertex is adjacent to all other vertices of the subgraph except at most k of them. A k-core is a maximal subgraph in which each vertex is adjacent to at least k other vertices of the subgraph. In any graph there is a whole hierarchy of cores of different order. An LS-set is a subgraph such that the internal degree of each vertex is greater than its external degree. A community is strong if the internal degree of any vertex exceeds the number of edges that the vertex shares with any other community. A community is weak if its total internal degree exceeds the number of edges shared by the community with the other communities. Another def focuses on robustness of clusters to edge removal and uses of edge connectivity. Edge connectivity of a pair of vertices is min # of edges need to be removed to disconnect (no path between). A lambda set is a subgraph s. t. any pair of vertices has larger edge connectivity than any pair formed by one vertex of the subgraph and one outside the subgraph. However, vertices of a lambda-set need not be adjacent and may be quite distant from each other. Communities can also be identified by a fitness measure, expressing to which extent a subgraph satisfies a given property related to its cohesion. The larger the fitness, the more definite is the community. This is the same principle behind quality functions, which give an estimate of the goodness of a graph partition. The simplest fitness measure for a cluster is its intra-cluster density int(C) (see slide 1). One could say subgraph C with k vertices is a cluster if int(C)>threshold. Finding such subgraphs is NP-complete, as it coincides with the NP-complete Clique Problem when the threshold =1. It is better to fix the size of the subgraph because, without this conditions, any clique would be one of the best possible communities, including trivial two-cliques (simple edges). Variants of this problem focus on the number of internal edges of the subgraph. k-plex’s are subgraphs s. t. each vertex is adjacent to all other vertices of the subgraph except at most k of them. k-plex existence algorithms: C is a k-plex iff v VC, |PUC| COMB(|VC|, 2) – k k-plex inheritance theorem: Every induced subgraph of a k-plex is a k-plex. Proof: Let C be an induced subgraph of G. A vertex of C cannot be missing more adjacent C-edges in C than it is missing adjacent C-edges as a vertex in G, because every missing edge in C is also missing in G (If an edge (v, w) is missing in the induced graph, C then since v, w are vertices in G, that edge (v, w) cannot be in E G, lest it would have been induced into C). Edge Count k-plex existence theorem: C is a k-plex iff |PUC| (|VC|!/((|VC|-2)!2!))-k Mining all maximal k-plexes: Start with G by checking |PUG|. If G is a k-plex, so are all induced subgraphs (Inheritance Thm. ) Done. Else check |PUC| induced subgraph C s. t. |VC|=|VG|-1. such C that is not a k-plex, check |PUD| induced subgraph, D of C s. t. |VD|=|VC|-1. Continue this until all induced subgraphs that are maximal k-plexes have been identified. A k-core is a subgraph in which each vertex is adjacent to at least k other vertices of the subgraph. There is a hierarchy of cores of different order. Edge Count k-core existence theorem: C is a k-core iff |PUC| k k-core inheritance theorem: If a cover of G by induced k-cores, then G is a k-core. Mining k-cores: If C is s k-core and D is a supergraph s. t. VD -VC={w 1, …, w. W}, D is s k-core iff deg. D(wh) k h=1. . W Note deg. D(w)=|PDU&PW| = |PD 0 n| where w is the nth vertex. So compute all |PD 0 k| then one can build the hierarchy of k-cores in D by examining the set of vertices where this deg is k=max. Any k-core, would have to be a subset of that set. Then go to k=max-1 Springer, May 2015 Charu C. Aggarwal. Comprehensive textbook on data mining (see secret site) Bipartite Communities Matthew P. Yancey Degree Calculations using p. Trees E 1 2 3 4 5 6 7 8 1 0 1 1 1 0 1 2 1 0 1 1 0 0 0 1 3 1 1 0 0 0 1 4 1 1 1 0 0 1 5 0 0 0 1 1 0 6 1 0 0 0 1 0 7 0 0 1 1 0 0 8 1 1 0 0 U 1 2 3 4 5 6 7 8 1 0 1 1 1 0 1 2 0 0 1 1 0 0 0 1 3 0 0 0 1 4 0 0 0 0 1 5 0 0 0 1 1 0 6 0 0 0 1 0 S. Fortunato, “Community Detection in Graphs. “ (see secret site). April 15, 2015 (see secret site) 6 5 7 0 0 0 0 8 0 0 0 0 7 2 1 4 3 8 Ec 0 1 1 1 0 1 2 1 0 1 1 0 0 0 1 3 1 1 0 0 0 1 4 1 1 1 0 0 1 5 0 0 0 1 1 0 6 1 0 0 0 1 0 Deg(Vk, C)=|PC&PVk|=|PCrk| V 1&Er 1 -8 = Er 0. 1 so we don’t need to precompute the 2 -level p. Trees but it saves 1 AND each time. Uc 0 1 1 1 0 1 Ec 1 0 1 1 1 1 7 8 0 1 0 1 1 0 0 0 Uc 1 1 1 1 0 0 2 0 0 1 1 0 0 0 1 3 0 0 0 1 Mohammad Zaki’s Data Mining book (See secret site) 4 0 0 0 0 1 5 0 0 0 1 1 0 6 0 0 0 1 0 Er 0 1 1 1 0 1 2 1 0 1 1 0 0 0 1 Ur 0 2 1 0 0 0 0 3 1 1 0 0 0 1 3 1 1 0 0 0 4 1 1 1 0 0 1 4 1 1 1 0 0 0 5 0 0 0 1 1 0 key 1 2 3 4 5 6 7 8 6 1 0 0 0 1 0 Er 1 1 1 1 1 7 8 0 1 0 1 1 0 0 0 6 1 0 0 0 Ur 1 0 1 1 7 8 0 1 0 1 1 0 0 0 Ec 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 1 1 0 1 0 0 0 0 1 1 0 0 Uc 0 1 1 1 0 1 0 0 1 1 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 key 1, 1 2, 1 3, 1 4, 1 5, 1 6, 1 7, 1 8, 1 1, 2 2, 2 3, 2 4, 2 5, 2 6, 2 7, 2 8, 2 1, 3 2, 3 3, 3 4, 3 5, 3 6, 3 7, 3 8, 3 1, 4 2, 4 3, 4 4, 4 5, 4 6, 4 7, 4 8, 4 1, 5 2, 5 3, 5 4, 5 5, 5 6, 5 7, 5 8, 5 1, 6 2, 6 3, 6 4, 6 5, 6 6, 6 7, 6 8, 6 1, 7 2, 7 3, 7 4, 7 5, 7 6, 7 7, 7 8, 7 1, 8 2, 8 3, 8 4, 8 5, 8 6, 8 7, 8 8, 8 V 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Er 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 1 1 0 1 0 0 0 0 1 1 0 0 Ur 0 0 0 0 1 1 0 0 0 1 1 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 key 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 2, 8 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 3, 8 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 4, 8 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 5, 8 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 6, 8 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 7, 8 8. 1 8, 2 8, 3 8, 4 8, 5 8, 6 8, 7 8. 8
Mining for Communities with more relaxed definitions than cliques (from Fortunatos survey) There are many cohesiveness definitions other than a Clique. Another criterion for subgraph cohesion relies idea that a vertex must be adjacent to some min # of other vertices. In social network analysis there are two complementary ways of expressing this. A k-plex is a maximal subgraph in which each vertex is adjacent to all other vertices of the subgraph except at most k of them. A k-core is a maximal subgraph in which each vertex is adjacent to at least k other vertices of the subgraph. In any graph there is a whole hierarchy of cores of different order. An LS-set is a subgraph such that the internal degree of each vertex is greater than its external degree. A community is strong if the internal degree of any vertex exceeds the number of edges that the vertex shares with any other community. A community is weak if its total internal degree exceeds the number of edges shared by the community with the other communities. Another def focuses on robustness of clusters to edge removal and uses of edge connectivity. Edge connectivity of a pair of vertices is min # of edges need to be removed to disconnect (no path between). A lambda set is a subgraph s. t. any pair of vertices has larger edge connectivity than any pair formed by one vertex of the subgraph and one outside the subgraph. However, vertices of a lambda-set need not be adjacent and may be quite distant from each other. Communities can also be identified by a fitness measure, expressing to which extent a subgraph satisfies a given property related to its cohesion. The larger the fitness, the more definite is the community. This is the same principle behind quality functions, which give an estimate of the goodness of a graph partition. The simplest fitness measure for a cluster is its intra-cluster density int(C) (see slide 1). One could say subgraph C with k vertices is a cluster if int(C)>threshold. Finding such subgraphs is NP-complete, as it coincides with the NP-complete Clique Problem when the threshold =1. It is better to fix the size of the subgraph because, without this conditions, any clique would be one of the best possible communities, including trivial two-cliques (simple edges). Variants of this problem focus on the number of internal edges of the subgraph. k-plex’s are subgraphs s. t. each vertex is adjacent to all other vertices of the subgraph except at most k of them. k-plex existence algorithms: C is a k-plex iff v VC, |PUC| COMB(|VC|, 2) – k k-plex inheritance theorem: Every induced subgraph of a k-plex is a k-plex. Proof: Let C be an induced subgraph of G. A vertex of C cannot be missing more adjacent C-edges in C than it is missing adjacent C-edges as a vertex in G, because every missing edge in C is also missing in G (If an edge (v, w) is missing in the induced graph, C then since v, w are vertices in G, that edge (v, w) cannot be in E G, lest it would have been induced into C). Edge Count k-plex existence theorem: C is a k-plex iff |PUC| (|VC|!/((|VC|-2)!2!))-k Mining all maximal k-plexes: Start with G by checking |PUG|. If G is a k-plex, so are all induced subgraphs (Inheritance Thm. ) Done. Else check |PUC| induced subgraph C s. t. |VC|=|VG|-1. such C that is not a k-plex, check |PUD| induced subgraph, D of C s. t. |VD|=|VC|-1. Continue this until all induced subgraphs that are maximal k-plexes have been identified. A k-core is a subgraph in which each vertex is adjacent to at least k other vertices of the subgraph. There is a hierarchy of cores of different order. Edge Count k-core existence theorem: C is a k-core iff |PUC| k k-core inheritance theorem: If a cover of G by induced k-cores, then G is a k-core. Mining k-cores: If C is s k-core and D is a supergraph s. t. VD -VC={w 1, …, w. W}, D is s k-core iff deg. D(wh) k h=1. . W Note deg. D(w)=|PDU&PW| = |PD 0 n| where w is the nth vertex. So compute all |PD 0 k| then one can build the hierarchy of k-cores in D by examining the set of vertices where this deg is k=max. Any k-core, would have to be a subset of that set. Then go to k=max-1 Springer, May 2015 Charu C. Aggarwal. Comprehensive textbook on data mining (see secret site) Bipartite Communities Matthew P. Yancey Degree Calculations using p. Trees E 1 2 3 4 5 6 7 8 1 0 1 1 1 0 1 2 1 0 1 1 0 0 0 1 3 1 1 0 0 0 1 4 1 1 1 0 0 1 5 0 0 0 1 1 0 6 1 0 0 0 1 0 7 0 0 1 1 0 0 8 1 1 0 0 U 1 2 3 4 5 6 7 8 1 0 1 1 1 0 1 2 0 0 1 1 0 0 0 1 3 0 0 0 1 4 0 0 0 0 1 5 0 0 0 1 1 0 6 0 0 0 1 0 S. Fortunato, “Community Detection in Graphs. “ (see secret site). April 15, 2015 (see secret site) 6 5 7 0 0 0 0 8 0 0 0 0 7 2 1 4 3 8 Ec 0 1 1 1 0 1 2 1 0 1 1 0 0 0 1 3 1 1 0 0 0 1 4 1 1 1 0 0 1 5 0 0 0 1 1 0 6 1 0 0 0 1 0 Deg(Vk, C)=|PC&PVk|=|PCrk| V 1&Er 1 -8 = Er 0. 1 so we don’t need to precompute the 2 -level p. Trees but it saves 1 AND each time. Uc 0 1 1 1 0 1 Ec 1 0 1 1 1 1 7 8 0 1 0 1 1 0 0 0 Uc 1 1 1 1 0 0 2 0 0 1 1 0 0 0 1 3 0 0 0 1 Mohammad Zaki’s Data Mining book (See secret site) 4 0 0 0 0 1 5 0 0 0 1 1 0 6 0 0 0 1 0 Er 0 1 1 1 0 1 2 1 0 1 1 0 0 0 1 Ur 0 2 1 0 0 0 0 3 1 1 0 0 0 1 3 1 1 0 0 0 4 1 1 1 0 0 1 4 1 1 1 0 0 0 5 0 0 0 1 1 0 key 1 2 3 4 5 6 7 8 6 1 0 0 0 1 0 Er 1 1 1 1 1 7 8 0 1 0 1 1 0 0 0 6 1 0 0 0 Ur 1 0 1 1 7 8 0 1 0 1 1 0 0 0 Ec 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 1 1 0 1 0 0 0 0 1 1 0 0 Uc 0 1 1 1 0 1 0 0 1 1 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 key 1, 1 2, 1 3, 1 4, 1 5, 1 6, 1 7, 1 8, 1 1, 2 2, 2 3, 2 4, 2 5, 2 6, 2 7, 2 8, 2 1, 3 2, 3 3, 3 4, 3 5, 3 6, 3 7, 3 8, 3 1, 4 2, 4 3, 4 4, 4 5, 4 6, 4 7, 4 8, 4 1, 5 2, 5 3, 5 4, 5 5, 5 6, 5 7, 5 8, 5 1, 6 2, 6 3, 6 4, 6 5, 6 6, 6 7, 6 8, 6 1, 7 2, 7 3, 7 4, 7 5, 7 6, 7 7, 7 8, 7 1, 8 2, 8 3, 8 4, 8 5, 8 6, 8 7, 8 8, 8 V 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Er 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 1 1 0 1 0 0 0 0 1 1 0 0 Ur 0 0 0 0 1 1 0 0 0 1 1 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 key 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1, 7 1, 8 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2, 7 2, 8 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3, 7 3, 8 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4, 7 4, 8 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 5, 8 6, 1 6, 2 6, 3 6, 4 6, 5 6, 6 6, 7 6, 8 7, 1 7, 2 7, 3 7, 4 7, 5 7, 6 7, 7 7, 8 8. 1 8, 2 8, 3 8, 4 8, 5 8, 6 8, 7 8. 8
 APPENDIX: A C, is confident if a high fraction of the f F which are related to every a A, are also related to every c C F is the Focus Entity and the high fraction is the Minimum. Confidence ratio. A hop is a relationship, R, hopping from entity, E, to entity, F. Supp. Set. A (set of F’s related to every element of A) = {2, 3, 5} F Supp. Set. C = {2, 4, 5} Strong Rule Mining finds all frequent, confident rules 2/3 = Conf. A C = |Supp. Set. A C|/|Supp. Set. A| SRMs are categorized by the number of hops, k, 4 = ct(&e A CPe) / ct(&e APe) A whether transitive or non-transitive and by the focus entity. 3 2 ARM is 1 -hop, non-transitive (A, C E), F-focused SRM (1 n. F) 1 0 0 1 1 1 0 1 C 2 1 -hop, transitive (A E, C F), F-focused SRM (1 t. F) ct(&e ARe &PC) / ct(&e ARe) mncf antecedent downward closure: If A is frequent, all subsets are frequent (A is infrequent, supersets infreq) Since frequency involves only A, we can mine for all qualifying antecedents using downward closure. E 1 1 0 0 F 5 1 1 1 ct(&e ARe) mnsp 3 4 1 1 1 0 1 1 R(E, F) Question: Why isn’t Conf. A C = Supp. C / Supp. A? consequent upward closure: If A C is non-confident, then so is A D for all subsets, D, of C. So frequent antecedent, A, use upward closure to mine for all of its' confident consequents. Transitive (a+c)-hop Apriori strong rule mining with a focus entity which is a hops from the antecedent and c hops from the consequent, if a/c is odd/even then one can use downward/upward closure on that step in the mining of strong (frequent and confident) rules. C G S(F, G) In this case A is 1 -hop from F (odd, use downward closure). C is 0 -hops from F (even, use upward closure). Even upward |A|=ct(PA) mnsp 1 -hop, transitive, E-focused rule, A C SRM (1 t. E) 2 -hop transitive F-focused 0 4 0 0 3 0 1 1 1 2 1 0 0 1 1 3 4 5 4 0 1 3 0 0 0 1 2 0 0 1 0 0 0 1 ct(PA&f CRf) / ct(PA) mncf C is 1 -hop from E (odd, use downward closure). A C strong if: ct(&e ARe) mnsp and 0 0 theorem seems to hold. antecedent upward closure: If A is infrequent, then so are all of its subsets. consequent downward closure) If A C is non-confident, then so is A D for all supersets, D, of C. In this case A is 0 -hops from E (even, use upward closure). 1 1 2 We will be checking more examples to see if the Odd downward 1 A E ct(&e ARe &g CSg) / ct(&e ARe) mncf F R(E, F) 1, 1 odd so down, down correct. Apriori for 2 -hops: Find all freq antecedents, A, using downward closure. 2, 0 even so up, up is correct. find C 1 G, the set of g's s. t. A {g} is confident. 0, 2 even so up, up is correct. Find C 2 G, set of C 1 G pairs that are confident consequents for antecedent, A. Find C 3 G, set of triples (from C 2 G) s. t. all subpairs are in C 2 G (ala Apriori), etc. ct(&f list& Re. Sf & PC) / &f list& Re. Sf mncf 2 -hop trans G-foc ct(&f list&e ARe. Sf) mnsp e A ct(&f l& Re. Sf) mnsp ct(&f & R Sf & PC) / &f & R Sf mncf 2 -hop trans E-foc ct(PA) mnsp ct(PA&f & e A e R) g CSg f / ct(PA) mncf antecedent upward closure: If A is infrequent, so are all subsets. 1. (antecedent upward closure) If A is infrequent, then so for are all subsets. 2. (consequent upward closure) If A C non-conf, so is A D for all subsets, D. consequent upward closuree: If A C non-conf so is A D for all subsets, D.
APPENDIX: A C, is confident if a high fraction of the f F which are related to every a A, are also related to every c C F is the Focus Entity and the high fraction is the Minimum. Confidence ratio. A hop is a relationship, R, hopping from entity, E, to entity, F. Supp. Set. A (set of F’s related to every element of A) = {2, 3, 5} F Supp. Set. C = {2, 4, 5} Strong Rule Mining finds all frequent, confident rules 2/3 = Conf. A C = |Supp. Set. A C|/|Supp. Set. A| SRMs are categorized by the number of hops, k, 4 = ct(&e A CPe) / ct(&e APe) A whether transitive or non-transitive and by the focus entity. 3 2 ARM is 1 -hop, non-transitive (A, C E), F-focused SRM (1 n. F) 1 0 0 1 1 1 0 1 C 2 1 -hop, transitive (A E, C F), F-focused SRM (1 t. F) ct(&e ARe &PC) / ct(&e ARe) mncf antecedent downward closure: If A is frequent, all subsets are frequent (A is infrequent, supersets infreq) Since frequency involves only A, we can mine for all qualifying antecedents using downward closure. E 1 1 0 0 F 5 1 1 1 ct(&e ARe) mnsp 3 4 1 1 1 0 1 1 R(E, F) Question: Why isn’t Conf. A C = Supp. C / Supp. A? consequent upward closure: If A C is non-confident, then so is A D for all subsets, D, of C. So frequent antecedent, A, use upward closure to mine for all of its' confident consequents. Transitive (a+c)-hop Apriori strong rule mining with a focus entity which is a hops from the antecedent and c hops from the consequent, if a/c is odd/even then one can use downward/upward closure on that step in the mining of strong (frequent and confident) rules. C G S(F, G) In this case A is 1 -hop from F (odd, use downward closure). C is 0 -hops from F (even, use upward closure). Even upward |A|=ct(PA) mnsp 1 -hop, transitive, E-focused rule, A C SRM (1 t. E) 2 -hop transitive F-focused 0 4 0 0 3 0 1 1 1 2 1 0 0 1 1 3 4 5 4 0 1 3 0 0 0 1 2 0 0 1 0 0 0 1 ct(PA&f CRf) / ct(PA) mncf C is 1 -hop from E (odd, use downward closure). A C strong if: ct(&e ARe) mnsp and 0 0 theorem seems to hold. antecedent upward closure: If A is infrequent, then so are all of its subsets. consequent downward closure) If A C is non-confident, then so is A D for all supersets, D, of C. In this case A is 0 -hops from E (even, use upward closure). 1 1 2 We will be checking more examples to see if the Odd downward 1 A E ct(&e ARe &g CSg) / ct(&e ARe) mncf F R(E, F) 1, 1 odd so down, down correct. Apriori for 2 -hops: Find all freq antecedents, A, using downward closure. 2, 0 even so up, up is correct. find C 1 G, the set of g's s. t. A {g} is confident. 0, 2 even so up, up is correct. Find C 2 G, set of C 1 G pairs that are confident consequents for antecedent, A. Find C 3 G, set of triples (from C 2 G) s. t. all subpairs are in C 2 G (ala Apriori), etc. ct(&f list& Re. Sf & PC) / &f list& Re. Sf mncf 2 -hop trans G-foc ct(&f list&e ARe. Sf) mnsp e A ct(&f l& Re. Sf) mnsp ct(&f & R Sf & PC) / &f & R Sf mncf 2 -hop trans E-foc ct(PA) mnsp ct(PA&f & e A e R) g CSg f / ct(PA) mncf antecedent upward closure: If A is infrequent, so are all subsets. 1. (antecedent upward closure) If A is infrequent, then so for are all subsets. 2. (consequent upward closure) If A C non-conf, so is A D for all subsets, D. consequent upward closuree: If A C non-conf so is A D for all subsets, D.
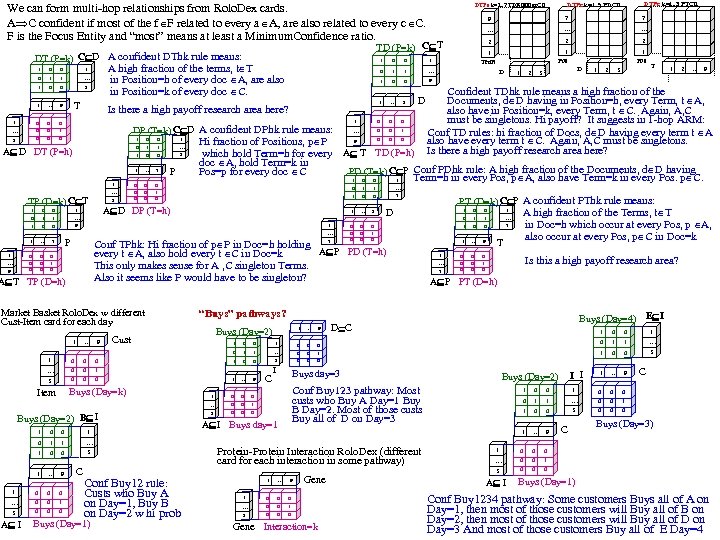 We can form multi-hop relationships from Rolo. Dex cards. A C confident if most of the f F related to every a A, are also related to every c C. F is the Focus Entity and “most” means at least a Minimum. Confidence ratio. 1 0 0 0 1 1 … 1 0 0 3 1 … 9 1 0 0 0 … 0 0 1 3 0 0 0 T 0 1 1 1 A D DT (P=h) 0 0 0 … 3 1 1 … 3 TP (D=k) C T 1 0 0 1 1 1 0 0 … 9 1 … 7 0 0 0 0 1 0 7 0 0 0 P … 9 … 3 0 0 0 … 0 0 1 9 0 0 D 0 A T TD (P=h) Market Basket Rolo. Dex w different Cust-Item card for each day 1 1 Pos Term D 1 2 D 3 1 0 0 1 1 1 Buys (Day=2) 9 3 T 0 0 … 3 … 9 0 0 0 1 … 7 1 1 0 0 … 7 1 1 0 1 0 0 0 … 9 0 0 0 0 1 0 T Is this a high payoff research area? A P PT (D=h) Buys (Day=4) E I D C 1 0 0 1 1 … 0 0 1 1 0 0 3 3 0 0 0 1 … 9 0 0 0 0 1 0 0 … 0 0 1 0 1 … 9 1 0 0 0 … 0 0 1 3 0 0 0 3 Buys (Day=k) Item Buys (Day=2) B I 1 0 0 1 1 … 1 0 0 3 1 … 9 1 0 0 0 … 0 0 1 0 3 A I C C I Buys day=3 Buys (Day=1) I I Buys (Day=2) Conf Buy 123 pathway: Most custs who Buy A Day=1 Buy B Day=2. Most of those custs Buy all of D on Day=3 Protein-Protein Interaction Rolo. Dex (different card for each interaction in some pathway) … 1 … 9 1 0 0 0 … 0 0 1 3 0 0 Gene Interaction=k A I 0 1 1 1 … 1 1 0 0 3 1 A I Buys day=1 1 3 Conf Buy 12 rule: Custs who Buy A on Day=1, Buy B on Day=2 w hi prob … 9 A high fraction of the Terms, t T in Doc=h which occur at every Pos, p A, also occur at every Pos, p C in Doc=k 1 Cust 2 PT (D=k) C P A confident PThk rule means: D 0 1 1 Term=h in every Pos, p A, also have Term=k in every Pos. p C. “Buys” pathways? … 2 Confident TDhk rule means a high fraction of the Documents, d D having in Position=h, every Term, t A, also have in Position=k, every Term, t C. Again, A, C must be singletons. Hi payoff? It suggests in 1 -hop ARM: Conf TD rules: hi fraction of Docs, d D having every term t A also have every term t C. Again, A, C must be singletons. Is there a high payoff research area here? … 7 1 1 1 PD (T=k) C P Conf PDhk rule: A high fraction of the Documents, d D having 7 Conf TPhk: Hi fraction of p P in Doc=h holding A P PD (T=h) every t A, also hold every t C in Doc=k This only makes sense for A , C singleton Terms. Also it seems like P would have to be singleton? A T TP (D=h) 2 1 9 1 … 1 0 0 1 P 0 … 2 … 1 0 A D DP (T=h) 1 0 … 0 0 0 1 1 Hi fraction of Positions, p P which hold Term=h for every doc A, hold Term=k in Pos=p for every doc C 1 7 … 2 1 1 DP (T=k) C D A confident DPhk rule means: 1 0 0 Is there a high payoff research area here? 0 7 … 1 A high fraction of the terms, t T in Position=h of every doc A, are also in Position=k of every doc C. 1 9 TD (P=k) C T DT (P=k) C D A confident DThk rule means: DTPe k=1. . 3 PTCd DTPe k=1. . 9 PDCd DTPe k=1. . 7 TDRolodex. Cd … 9 0 0 0 C 0 1 0 C Buys (Day=3) Buys (Day=1) Conf Buy 1234 pathway: Some customers Buys all of A on Day=1, then most of those customers will Buy all of B on Day=2, then most of those customers will Buy all of D on Day=3 And most of those customers Buy all of E Day=4
We can form multi-hop relationships from Rolo. Dex cards. A C confident if most of the f F related to every a A, are also related to every c C. F is the Focus Entity and “most” means at least a Minimum. Confidence ratio. 1 0 0 0 1 1 … 1 0 0 3 1 … 9 1 0 0 0 … 0 0 1 3 0 0 0 T 0 1 1 1 A D DT (P=h) 0 0 0 … 3 1 1 … 3 TP (D=k) C T 1 0 0 1 1 1 0 0 … 9 1 … 7 0 0 0 0 1 0 7 0 0 0 P … 9 … 3 0 0 0 … 0 0 1 9 0 0 D 0 A T TD (P=h) Market Basket Rolo. Dex w different Cust-Item card for each day 1 1 Pos Term D 1 2 D 3 1 0 0 1 1 1 Buys (Day=2) 9 3 T 0 0 … 3 … 9 0 0 0 1 … 7 1 1 0 0 … 7 1 1 0 1 0 0 0 … 9 0 0 0 0 1 0 T Is this a high payoff research area? A P PT (D=h) Buys (Day=4) E I D C 1 0 0 1 1 … 0 0 1 1 0 0 3 3 0 0 0 1 … 9 0 0 0 0 1 0 0 … 0 0 1 0 1 … 9 1 0 0 0 … 0 0 1 3 0 0 0 3 Buys (Day=k) Item Buys (Day=2) B I 1 0 0 1 1 … 1 0 0 3 1 … 9 1 0 0 0 … 0 0 1 0 3 A I C C I Buys day=3 Buys (Day=1) I I Buys (Day=2) Conf Buy 123 pathway: Most custs who Buy A Day=1 Buy B Day=2. Most of those custs Buy all of D on Day=3 Protein-Protein Interaction Rolo. Dex (different card for each interaction in some pathway) … 1 … 9 1 0 0 0 … 0 0 1 3 0 0 Gene Interaction=k A I 0 1 1 1 … 1 1 0 0 3 1 A I Buys day=1 1 3 Conf Buy 12 rule: Custs who Buy A on Day=1, Buy B on Day=2 w hi prob … 9 A high fraction of the Terms, t T in Doc=h which occur at every Pos, p A, also occur at every Pos, p C in Doc=k 1 Cust 2 PT (D=k) C P A confident PThk rule means: D 0 1 1 Term=h in every Pos, p A, also have Term=k in every Pos. p C. “Buys” pathways? … 2 Confident TDhk rule means a high fraction of the Documents, d D having in Position=h, every Term, t A, also have in Position=k, every Term, t C. Again, A, C must be singletons. Hi payoff? It suggests in 1 -hop ARM: Conf TD rules: hi fraction of Docs, d D having every term t A also have every term t C. Again, A, C must be singletons. Is there a high payoff research area here? … 7 1 1 1 PD (T=k) C P Conf PDhk rule: A high fraction of the Documents, d D having 7 Conf TPhk: Hi fraction of p P in Doc=h holding A P PD (T=h) every t A, also hold every t C in Doc=k This only makes sense for A , C singleton Terms. Also it seems like P would have to be singleton? A T TP (D=h) 2 1 9 1 … 1 0 0 1 P 0 … 2 … 1 0 A D DP (T=h) 1 0 … 0 0 0 1 1 Hi fraction of Positions, p P which hold Term=h for every doc A, hold Term=k in Pos=p for every doc C 1 7 … 2 1 1 DP (T=k) C D A confident DPhk rule means: 1 0 0 Is there a high payoff research area here? 0 7 … 1 A high fraction of the terms, t T in Position=h of every doc A, are also in Position=k of every doc C. 1 9 TD (P=k) C T DT (P=k) C D A confident DThk rule means: DTPe k=1. . 3 PTCd DTPe k=1. . 9 PDCd DTPe k=1. . 7 TDRolodex. Cd … 9 0 0 0 C 0 1 0 C Buys (Day=3) Buys (Day=1) Conf Buy 1234 pathway: Some customers Buys all of A on Day=1, then most of those customers will Buy all of B on Day=2, then most of those customers will Buy all of D on Day=3 And most of those customers Buy all of E Day=4
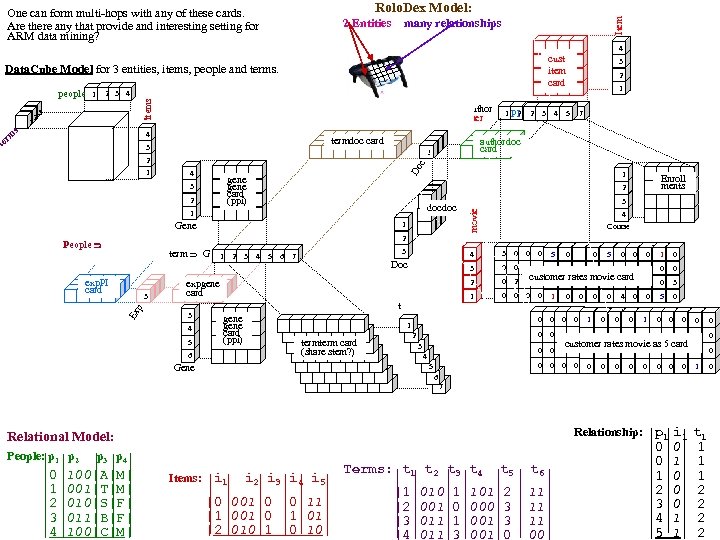 2 Entities Item Rolo. Dex Model: One can form multi-hops with any of these cards. Are there any that provide and interesting setting for ARM data mining? many relationships 4 cust item card Data. Cube Model for 3 entities, items, people and terms. People Author Customer 4 rm te termdoc card 3 1 1 4 gene card (ppi) 3 2 1 1 1 PI 3 4 4 5 2 2 3 5 6 7 1 authordoc 1 1 card 1 1 1 Do c 2 1 1 1 docdoc 1 1 Gene 1 Enroll ments 2 1 3 movie 3 s 1 2 2 3 4 5 1 items people 3 4 Course 2 People term G exp. PI card 1 1 3 4 5 6 3 7 Ex 4 3 0 0 Doc 3 0 0 2 2 0 2 1 0 0 0 expgene card 3 4 5 gene card (ppi) 6 4 5 0 1 0 0 3 0 0 5 0 0 0 0 0 1 0 0 4 0 0 0 1 0 customer rates movie card 0 2 Gene 5 0 1 term card (share stem? ) 0 0 t p 3 1 3 5 0 0 0 customer rates movie as 5 card 0 0 0 1 6 7 Relationship: p 1 i 1 t 1 Relational Model: People: p 1 p 2 |0 |1 |2 |3 |4 p 3 p 4 100|A|M| 001|T|M| 010|S|F| 011|B|F| 100|C|M| Items: i 1 i 2 i 3 i 4 i 5 |0 001|0 |0 11| |1 001|0 |1 01| |2 010|1 |0 10| Terms: t 1 t 2 t 3 t 4 |1 |2 |3 |4 010|1 001|0 011|1 011|3 t 5 101|2 000|3 001|0 t 6 11| 11| 00| |0 |0 |1 |2 |3 |4 |5 0 0| 1 1| 1 0| 2 1|_2 0
2 Entities Item Rolo. Dex Model: One can form multi-hops with any of these cards. Are there any that provide and interesting setting for ARM data mining? many relationships 4 cust item card Data. Cube Model for 3 entities, items, people and terms. People Author Customer 4 rm te termdoc card 3 1 1 4 gene card (ppi) 3 2 1 1 1 PI 3 4 4 5 2 2 3 5 6 7 1 authordoc 1 1 card 1 1 1 Do c 2 1 1 1 docdoc 1 1 Gene 1 Enroll ments 2 1 3 movie 3 s 1 2 2 3 4 5 1 items people 3 4 Course 2 People term G exp. PI card 1 1 3 4 5 6 3 7 Ex 4 3 0 0 Doc 3 0 0 2 2 0 2 1 0 0 0 expgene card 3 4 5 gene card (ppi) 6 4 5 0 1 0 0 3 0 0 5 0 0 0 0 0 1 0 0 4 0 0 0 1 0 customer rates movie card 0 2 Gene 5 0 1 term card (share stem? ) 0 0 t p 3 1 3 5 0 0 0 customer rates movie as 5 card 0 0 0 1 6 7 Relationship: p 1 i 1 t 1 Relational Model: People: p 1 p 2 |0 |1 |2 |3 |4 p 3 p 4 100|A|M| 001|T|M| 010|S|F| 011|B|F| 100|C|M| Items: i 1 i 2 i 3 i 4 i 5 |0 001|0 |0 11| |1 001|0 |1 01| |2 010|1 |0 10| Terms: t 1 t 2 t 3 t 4 |1 |2 |3 |4 010|1 001|0 011|1 011|3 t 5 101|2 000|3 001|0 t 6 11| 11| 00| |0 |0 |1 |2 |3 |4 |5 0 0| 1 1| 1 0| 2 1|_2 0
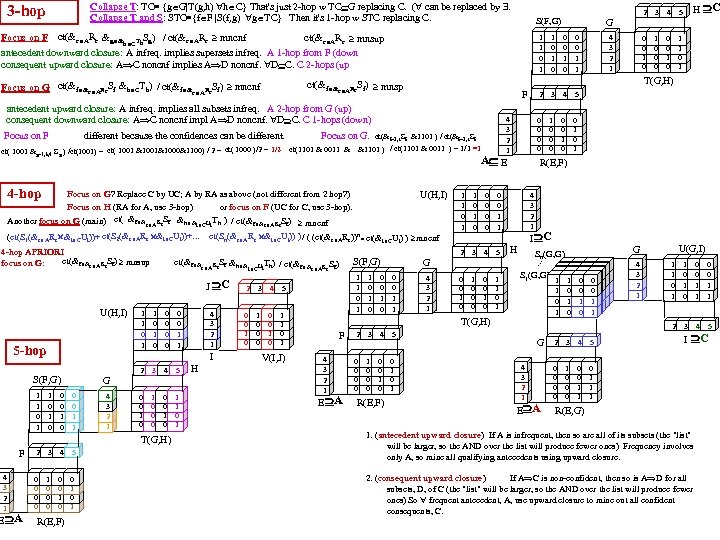 Collapse T: TC≡ {g G|T(g, h) h C} That's just 2 -hop w TC G replacing C. ( can be replaced by . Collapse T and S: STC≡{f F |S(f, g) g TC} Then it's 1 -hop w STC replacing C. 3 -hop Focus on F ct(&e ARe &g & Th. Sg) / ct(&e ARe mncnf ct(&e ARe mnsup h C antecedent downward closure: A infreq. implies supersets infreq. A 1 -hop from F (down consequent upward closure: A C noncnf implies A D noncnf. D C. C 2 -hops (up A E U(H, I) Focus on G? Replace C by UC; A by RA as above (not different from 2 hop? ) Focus on H (RA for A, use 3 -hop) or focus on F (UC for C, use 3 -hop). Another focus on G (main) ct( &f &e ARe. Sf &h &i CUi. Th ) / ct(&f &e ARe. Sf) mncnf (ct(S 1(&e ARe &i CUi))+ ct(S 2(&e ARe &i CUi))+. . . 4 -hop APRIORI ct(&f &e ARe. Sf) mnsup focus on G: J C U(H, I) 0 0 0 1 1 3 4 5 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 G 0 0 1 1 4 3 2 1 T(G, H) F 4 3 2 1 E A 4 3 2 1 I S(F, G) 1 1 0 1 0 2 5 -hop 1 1 0 1 2 3 4 5 0 0 0 0 1 0 1 0 R(E, F) H 2 3 4 1 0 0 0 1 1 0 1 V(I, J) 1 0 0 0 1 0 0 0 1 1 2 3 4 1 0 0 1 0 1 4 4 3 2 1 E A 0 0 1 0 R(E, F) 1 0 0 0 1 1 0 1 5 1 0 0 0 1 0 1 4 3 2 1 3 4 5 4 3 2 1 I C H 4 3 2 1 0 0 0 1 1 0 1 U(G, I) G Sn(G, G) 1 0 0 0 1 1 1 0 11 00 00 11 1 1 0 0 1 G 4 3 2 1 E A 2 3 4 5 0 0 1 0 0 0 4 3 2 1 1 1 0 1 0 2 1 S 1(G, G) 1111 110 000 11 00 00 0 1 00 11 11 11 0 0 0 5 0 0 3 T(G, H) F 0 0 1 0 H C 5 R(E, F) 0 0 1 1 G 1 1 0 1 5 0 0 1 0 S(F, G) 1 1 0 1 2 ct(Sn(&e ARe &i CUi)) ) / ( (ct(&e ARe))n * ct(&i CUi) ) mncnf ct(&f &e ARe. Sf &h & Ui. Th) / ct(&f & R Sf) e A e i C 0 0 1 1 0 0 4 3 2 1 ct(&f=2, 5 Sf &1101 ) / ct(1101 & 0011 ) = 1/1 =1 4 -hop 4 T(G, H) Focus on G. ct(1101 & 0011 & ct( 1001 &g=1, 3, 4 Sg ) /ct(1001) = ct( 1001 &1001&1000&1100) / 2 = ct( 1000 )/2 = 1/2 0 0 1 0 . . . different because the confidences can be different. 1 0 2 F antecedent upward closure: A infreq. implies all subsets infreq. A 2 -hop from G (up) consequent downward closure: A C noncnf impl A D noncnf. D C. C 1 -hops (down) Focus on F 3 G 1 1 0 1 ct(&f &e ARe. Sf) mnsp Focus on G ct(&f &e ARe. Sf &h CTh) / ct(&f &e ARe. Sf) mncnf 2 S(F, G) 3 I 0 0 1 1 4 5 C 0 1 1 1 0 0 1 1 R(E, G) 1. (antecedent upward closure) If A is infrequent, then so are all of its subsets (the "list" will be larger, so the AND over the list will produce fewer ones) Frequency involves only A, so mine all qualifying antecedents using upward closure. 2. (consequent upward closure) If A C is non-confident, then so is A D for all subsets, D, of C (the "list" will be larger, so the AND over the list will produce fewer ones) So frequent antecedent, A, use upward closure to mine out all confident consequents, C.
Collapse T: TC≡ {g G|T(g, h) h C} That's just 2 -hop w TC G replacing C. ( can be replaced by . Collapse T and S: STC≡{f F |S(f, g) g TC} Then it's 1 -hop w STC replacing C. 3 -hop Focus on F ct(&e ARe &g & Th. Sg) / ct(&e ARe mncnf ct(&e ARe mnsup h C antecedent downward closure: A infreq. implies supersets infreq. A 1 -hop from F (down consequent upward closure: A C noncnf implies A D noncnf. D C. C 2 -hops (up A E U(H, I) Focus on G? Replace C by UC; A by RA as above (not different from 2 hop? ) Focus on H (RA for A, use 3 -hop) or focus on F (UC for C, use 3 -hop). Another focus on G (main) ct( &f &e ARe. Sf &h &i CUi. Th ) / ct(&f &e ARe. Sf) mncnf (ct(S 1(&e ARe &i CUi))+ ct(S 2(&e ARe &i CUi))+. . . 4 -hop APRIORI ct(&f &e ARe. Sf) mnsup focus on G: J C U(H, I) 0 0 0 1 1 3 4 5 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 G 0 0 1 1 4 3 2 1 T(G, H) F 4 3 2 1 E A 4 3 2 1 I S(F, G) 1 1 0 1 0 2 5 -hop 1 1 0 1 2 3 4 5 0 0 0 0 1 0 1 0 R(E, F) H 2 3 4 1 0 0 0 1 1 0 1 V(I, J) 1 0 0 0 1 0 0 0 1 1 2 3 4 1 0 0 1 0 1 4 4 3 2 1 E A 0 0 1 0 R(E, F) 1 0 0 0 1 1 0 1 5 1 0 0 0 1 0 1 4 3 2 1 3 4 5 4 3 2 1 I C H 4 3 2 1 0 0 0 1 1 0 1 U(G, I) G Sn(G, G) 1 0 0 0 1 1 1 0 11 00 00 11 1 1 0 0 1 G 4 3 2 1 E A 2 3 4 5 0 0 1 0 0 0 4 3 2 1 1 1 0 1 0 2 1 S 1(G, G) 1111 110 000 11 00 00 0 1 00 11 11 11 0 0 0 5 0 0 3 T(G, H) F 0 0 1 0 H C 5 R(E, F) 0 0 1 1 G 1 1 0 1 5 0 0 1 0 S(F, G) 1 1 0 1 2 ct(Sn(&e ARe &i CUi)) ) / ( (ct(&e ARe))n * ct(&i CUi) ) mncnf ct(&f &e ARe. Sf &h & Ui. Th) / ct(&f & R Sf) e A e i C 0 0 1 1 0 0 4 3 2 1 ct(&f=2, 5 Sf &1101 ) / ct(1101 & 0011 ) = 1/1 =1 4 -hop 4 T(G, H) Focus on G. ct(1101 & 0011 & ct( 1001 &g=1, 3, 4 Sg ) /ct(1001) = ct( 1001 &1001&1000&1100) / 2 = ct( 1000 )/2 = 1/2 0 0 1 0 . . . different because the confidences can be different. 1 0 2 F antecedent upward closure: A infreq. implies all subsets infreq. A 2 -hop from G (up) consequent downward closure: A C noncnf impl A D noncnf. D C. C 1 -hops (down) Focus on F 3 G 1 1 0 1 ct(&f &e ARe. Sf) mnsp Focus on G ct(&f &e ARe. Sf &h CTh) / ct(&f &e ARe. Sf) mncnf 2 S(F, G) 3 I 0 0 1 1 4 5 C 0 1 1 1 0 0 1 1 R(E, G) 1. (antecedent upward closure) If A is infrequent, then so are all of its subsets (the "list" will be larger, so the AND over the list will produce fewer ones) Frequency involves only A, so mine all qualifying antecedents using upward closure. 2. (consequent upward closure) If A C is non-confident, then so is A D for all subsets, D, of C (the "list" will be larger, so the AND over the list will produce fewer ones) So frequent antecedent, A, use upward closure to mine out all confident consequents, C.
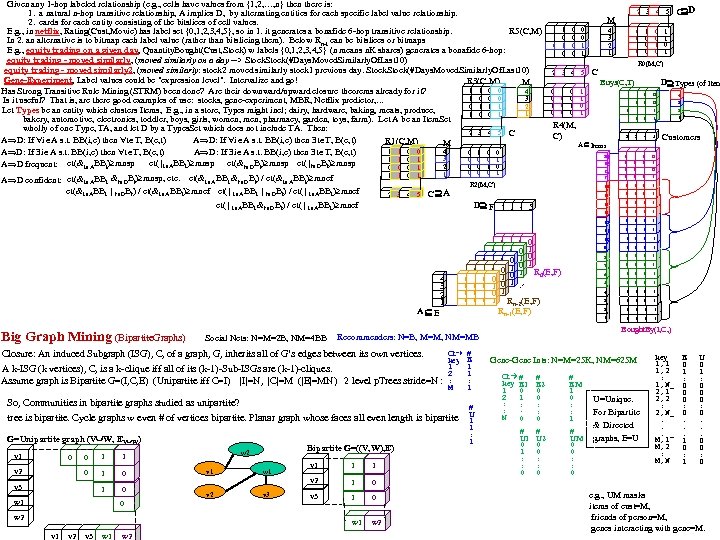 Given any 1 -hop labeled relationship (e. g. , cells have values from {1, 2, …, n} then there is: 1. a natural n-hop transitive relationship, A implies D, by alternating entities for each specific label value relationship. 2. cards for each entity consisting of the bitslices of cell values. R 5(C, M) E. g. , in netflix, Rating(Cust, Movie) has label set {0, 1, 2, 3, 4, 5}, so in 1. it generates a bonafide 6 -hop transitive relationship. In 2. an alternative is to bitmap each label value (rather than bitslicing them). Below R n-i can be bitslices or bitmaps E. g. , equity trading on a given day, Quantity. Bought(Cust, Stock) w labels {0, 1, 2, 3, 4, 5} (n means n. K shares) generates a bonafide 6 -hop: equity trading - moved similarly, (moved similarly on a day --> Stock(#Days. Moved. Similarly. Of. Last 10) equity trading - moved similarly 2, (moved similarly: stock 2 moved similarly stock 1 previous day. Stock(#Days. Moved. Similarly. Of. Last 10) Gene-Experiment, Label values could be "expression level". Intervalize and go! R 3(C, M) M 1 1 0 0 4 Has Strong Transitive Rule Mining (STRM) been done? Are their downward/upward closure theorems already for it? 1 0 0 0 3 Is it useful? That is, are there good examples of use: stocks, gene-experiment, MBR, Netflix predictor, . . . 0 1 1 1 2 Let Types be an entity which clusters Items, E. g. , in a store, Types might incl; dairy, hardware, baking, meats, produce, 1 1 0 0 1 bakery, automotive, electronics, toddler, boys, girls, women, pharmacy, garden, toys, farm). Let A be an Item. Set wholly of one Type, TA, and let D by a Types. Set which does not include TA. Then: 2 3 4 5 C A D: If i A s. t. BB(i, c) then t T, B(c, t) R 1(C, M) M 1 1 0 0 4 A D: If i A s. t. BB(i, c) then t T, B(c, t) 0 1 0 0 3 0 0 0 1 1 1 0 1 ct( |i ABBi) mnsp ct(&t DBt) mnsp ct( |t DBt) mnsp A D frequent: ct(&i ABBi) mnsp 0 0 1 0 2 0 0 0 1 2 3 4 5 M 1 1 0 1 0 0 0 0 1 1 4 3 2 1 0 0 0 1 0 C Buys(C, T) 0 0 1 0 R 4(M, C) 1 1 0 1 D Types (of Item 1 1 0 0 0 0 1 1 0 0 1 2 3 4 5 1 0 0 0 1 0 1 A Items 18 17 0 0 R 2(M, C) 16 0 0 0 1 0 0 0 1 10 0 1 9 0 0 0 1 8 0 0 0 1 7 0 0 0 1 6 0 0 0 1 5 0 0 0 1 4 0 0 0 1 3 0 0 0 1 2 0 0 0 1 1 0 0 0 1 C A A E Social Nets: N=M=2 B, NM=4 BB 0 0 Ct key 1 2 : M So, Communities in bipartite graphs studied as unipartite? tree is bipartite. Cycle graphs w even # of vertices bipartite. Planar graph whose faces all even length is bipartite v 1 0 1 0 Bipartite G=((V, W), E) w 2 1 0 0 v 3 w 1 0 w 2 v 1 v 2 v 3 w 1 w 2 v 2 w 1 v 3 1 1 v 2 v 1 1 0 0 0 1 1 0 0 1 0 1 R 0(E, F) Rn-2(E, F) Rn-1(E, F) Bought. By(I, C, ) 1 0 w 2 # E 1 1 : 1 # U 1 1 : 1 Gene-Gene Ints: N=M=25 K, NM=625 M Ct # key E 1 1 0 2 1 : : N 0 # E 2 0 0 : : 0 # EM 1 0 : : 1 # U 1 0 1 : : 0 # U 2 0 0 : : 0 # UM 0 0 : : 0 U=Unique. For Bipartite & Directed graphs, E=U key 1, 1 1, 2 : 1, N_ 2, 1 2, 2 : 2, N_. . . _ M, 1 M, 2 : M, N E 0 1 : 0 0 0 : 0. . . 1 0 : 1 U 0 1 : 0 0 0 : 0. . . 0 0 : 0 0 v 3 w 1 v 2 0 0 1 0 0 0 0 1 1 0 0 1 Recommenders: N=B, M=M, NM=MB Closure: An induced Subgraph (ISG), C, of a graph, G, inherits all of G’s edges between its own vertices. A k-ISG (k vertices), C, is a k-clique iff all of its (k-1)-Sub-ISGs are (k-1)-cliques. Assume graph is Bipartite G=(I, C, E) (Unipartite iff C=I) |I|=N, |C|=M (|E|=MN) 2 level p. Trees stride=N : G=Unipartite graph (V W, EV W) 0 0 1 0 0 0 0 0 1 1 0 0 1 . . . ct( | i ABBi &t DBt) / ct( | i ABBi) mncf Big Graph Mining (Bipartite. Graphs) 20 19 D F 2 3 4 5 4 3 2 1 Customers 1 13 2 1 1 14 4 3 1 15 12 2 3 4 5 1 1 0 1 R 0(M, C) 2 3 4 5 0 0 0 1 1 0 1 A D confident: ct(&i ABBi &t DBt) mnsp, etc. ct(&i ABBi &t DBt) / ct(&i ABBi) mncf ct(&i ABBi | t DBt) / ct(&i ABBi) mncf ct( | i ABBi | t DBt) / ct( | i ABBi) mncf C D e. g. , UM masks items of cust=M, friends of person=M, genes interacting with gene=M.
Given any 1 -hop labeled relationship (e. g. , cells have values from {1, 2, …, n} then there is: 1. a natural n-hop transitive relationship, A implies D, by alternating entities for each specific label value relationship. 2. cards for each entity consisting of the bitslices of cell values. R 5(C, M) E. g. , in netflix, Rating(Cust, Movie) has label set {0, 1, 2, 3, 4, 5}, so in 1. it generates a bonafide 6 -hop transitive relationship. In 2. an alternative is to bitmap each label value (rather than bitslicing them). Below R n-i can be bitslices or bitmaps E. g. , equity trading on a given day, Quantity. Bought(Cust, Stock) w labels {0, 1, 2, 3, 4, 5} (n means n. K shares) generates a bonafide 6 -hop: equity trading - moved similarly, (moved similarly on a day --> Stock(#Days. Moved. Similarly. Of. Last 10) equity trading - moved similarly 2, (moved similarly: stock 2 moved similarly stock 1 previous day. Stock(#Days. Moved. Similarly. Of. Last 10) Gene-Experiment, Label values could be "expression level". Intervalize and go! R 3(C, M) M 1 1 0 0 4 Has Strong Transitive Rule Mining (STRM) been done? Are their downward/upward closure theorems already for it? 1 0 0 0 3 Is it useful? That is, are there good examples of use: stocks, gene-experiment, MBR, Netflix predictor, . . . 0 1 1 1 2 Let Types be an entity which clusters Items, E. g. , in a store, Types might incl; dairy, hardware, baking, meats, produce, 1 1 0 0 1 bakery, automotive, electronics, toddler, boys, girls, women, pharmacy, garden, toys, farm). Let A be an Item. Set wholly of one Type, TA, and let D by a Types. Set which does not include TA. Then: 2 3 4 5 C A D: If i A s. t. BB(i, c) then t T, B(c, t) R 1(C, M) M 1 1 0 0 4 A D: If i A s. t. BB(i, c) then t T, B(c, t) 0 1 0 0 3 0 0 0 1 1 1 0 1 ct( |i ABBi) mnsp ct(&t DBt) mnsp ct( |t DBt) mnsp A D frequent: ct(&i ABBi) mnsp 0 0 1 0 2 0 0 0 1 2 3 4 5 M 1 1 0 1 0 0 0 0 1 1 4 3 2 1 0 0 0 1 0 C Buys(C, T) 0 0 1 0 R 4(M, C) 1 1 0 1 D Types (of Item 1 1 0 0 0 0 1 1 0 0 1 2 3 4 5 1 0 0 0 1 0 1 A Items 18 17 0 0 R 2(M, C) 16 0 0 0 1 0 0 0 1 10 0 1 9 0 0 0 1 8 0 0 0 1 7 0 0 0 1 6 0 0 0 1 5 0 0 0 1 4 0 0 0 1 3 0 0 0 1 2 0 0 0 1 1 0 0 0 1 C A A E Social Nets: N=M=2 B, NM=4 BB 0 0 Ct key 1 2 : M So, Communities in bipartite graphs studied as unipartite? tree is bipartite. Cycle graphs w even # of vertices bipartite. Planar graph whose faces all even length is bipartite v 1 0 1 0 Bipartite G=((V, W), E) w 2 1 0 0 v 3 w 1 0 w 2 v 1 v 2 v 3 w 1 w 2 v 2 w 1 v 3 1 1 v 2 v 1 1 0 0 0 1 1 0 0 1 0 1 R 0(E, F) Rn-2(E, F) Rn-1(E, F) Bought. By(I, C, ) 1 0 w 2 # E 1 1 : 1 # U 1 1 : 1 Gene-Gene Ints: N=M=25 K, NM=625 M Ct # key E 1 1 0 2 1 : : N 0 # E 2 0 0 : : 0 # EM 1 0 : : 1 # U 1 0 1 : : 0 # U 2 0 0 : : 0 # UM 0 0 : : 0 U=Unique. For Bipartite & Directed graphs, E=U key 1, 1 1, 2 : 1, N_ 2, 1 2, 2 : 2, N_. . . _ M, 1 M, 2 : M, N E 0 1 : 0 0 0 : 0. . . 1 0 : 1 U 0 1 : 0 0 0 : 0. . . 0 0 : 0 0 v 3 w 1 v 2 0 0 1 0 0 0 0 1 1 0 0 1 Recommenders: N=B, M=M, NM=MB Closure: An induced Subgraph (ISG), C, of a graph, G, inherits all of G’s edges between its own vertices. A k-ISG (k vertices), C, is a k-clique iff all of its (k-1)-Sub-ISGs are (k-1)-cliques. Assume graph is Bipartite G=(I, C, E) (Unipartite iff C=I) |I|=N, |C|=M (|E|=MN) 2 level p. Trees stride=N : G=Unipartite graph (V W, EV W) 0 0 1 0 0 0 0 0 1 1 0 0 1 . . . ct( | i ABBi &t DBt) / ct( | i ABBi) mncf Big Graph Mining (Bipartite. Graphs) 20 19 D F 2 3 4 5 4 3 2 1 Customers 1 13 2 1 1 14 4 3 1 15 12 2 3 4 5 1 1 0 1 R 0(M, C) 2 3 4 5 0 0 0 1 1 0 1 A D confident: ct(&i ABBi &t DBt) mnsp, etc. ct(&i ABBi &t DBt) / ct(&i ABBi) mncf ct(&i ABBi | t DBt) / ct(&i ABBi) mncf ct( | i ABBi | t DBt) / ct( | i ABBi) mncf C D e. g. , UM masks items of cust=M, friends of person=M, genes interacting with gene=M.
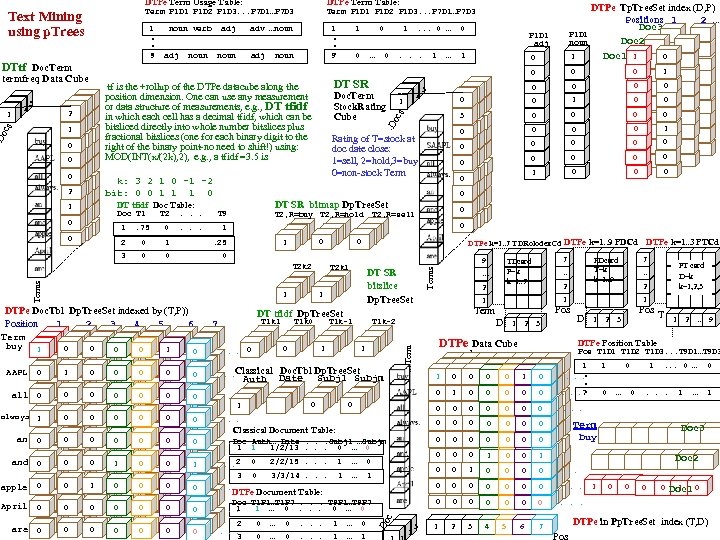 DTPe Term Usage Table: DTtf Doc. Term 2 s 1 oc noun adj 1 0 0 0 noun DT tfidf Doc Table: 1 Doc T 1 0 T 2 . . . 0 2 0 1 . 25 0 0 Terms T 1 k 1 1 0 0 0 0 0 all 0 0 0 0 0 1 0 0 0 10 0 00 0 10 0 0 0 0 0 0 DTPe k=1. . 7 TDRolodex. Cd DTPe k=1. . 9 PDCd 9 T 2 k 1 DT SR bitslice Dp. Tree. Set 1 always 1 0 0 T 1 k 0 0 . . . 1 . . . 0 … 2 2 T 1 k-1 1 1 Auth D 1 2 3 DTPe Data Cube 1 0 0 0 0 and 0 0 0 1 apple 0 0 1 0 0 April 0 0 0 0 are 0 0 0 0 2. . . 3 2/2/15. . . 1 … 0 0 3/3/14. . . 1 … 0 0 … 0 . . . 1 … 1 . D o 0 0 1. . 1 0 0 0 . . 7 0 0 0 2 3 T 1 2 … 9 . . . 0 0 0 0 1 0 0 0 0 . . . 1 2 3 4 c DTPe Document Table: 1 0 Doc T 1 P 1…T 1 P 7. . . T 9 P 1…T 9 P 7 1 … 0. . . 0 … 0. . 1. 0 0 0 . . Doc Auth… Date. . . Subj 1 …Subjm. 1 1 1/2/13. . . 0 … 0 0 0 Classical Document Table: 0 0 0 1 Pos T 1 D 1 T 1 D 2 T 1 D 3. . . T 9 D 1…T 9 D 3 0 0 Pos DTPe Position Table 0 Doc. Tbl Dp. Tree. Set Date Subj 1 Subjm 2 1 Pos D T 1 k-2 PT card D=k k=1, 2, 3 … 1 Term DTPe k=1. . 3 PTCd 7 PDcard T=k k=1. . 9 … 0 . . . Classical . . . 2 3. . . 7 TDcard P=k k=1. . 7 1 . . . 0 0 0 3 0 . . . Term 0 0 0 3 2 1 T 2, R=sell DT tfidf Dp. Tree. Set 7 0 an 0 1 0 0 … P 1 D 1 adj 0 0 0 1 1 . 75 DTPe Doc. Tbl Dp. Tree. Set indexed by (T, P)) Position 1 2 3 4 5 6 Term AAPL . . . 0 Rating of T=stock at doc date close: 1=sell, 2=hold, 3=buy 0=non-stock Term T 2, R=buy T 2, R=hold 1 0 0 Doc. Term Stock. Rating Cube T 2 k 2 1 … . . . 0 … DT SR bitmap Dp. Tree. Set T 9 3 buy 0 1 0 0 DT SR k: 3 2 1 0 -1 -2 bit: 0 0 1 1 1 0 2 1 . . . 9 tf is the +rollup of the DTPe datacube along the position dimension. One can use any measurement or data structure of measurements, e. g. , DT tfidf in which each cell has a decimal tfidf, which can be bitsliced directly into whole number bitslices plus fractional bitslices (one for each binary digit to the right of the binary point-no need to shift!) using: MOD(INT(x/(2 k), 2), e. g. , a tfidf =3. 5 is 3 . D noun adv …noun . D 2 adj Terms termfreq Data Cube noun verb s . . . 9 Term P 1 D 1 P 1 D 2 P 1 D 3. . . P 7 D 1…P 7 D 3 oc 1 DTPe Tp. Tree. Set index (D, P) Positions 1 2 … Doc 3 1 1 P 1 D 1 Doc 2 1 noun 1 0 0 Doc 1 1 0 0 0 1 0 Text Mining using p. Trees 1 DTPe Term Table: Term P 1 D 1 P 1 D 2 P 1 D 3. . . P 7 D 1…P 7 D 3 5 6 7 1 0 1 . . . 0 … 0 . . . Term buy 1 … 1 Doc 3 Doc 2 1 0 0 1 Doc 1 0 DTPe in Pp. Tree. Set index (T, D)
DTPe Term Usage Table: DTtf Doc. Term 2 s 1 oc noun adj 1 0 0 0 noun DT tfidf Doc Table: 1 Doc T 1 0 T 2 . . . 0 2 0 1 . 25 0 0 Terms T 1 k 1 1 0 0 0 0 0 all 0 0 0 0 0 1 0 0 0 10 0 00 0 10 0 0 0 0 0 0 DTPe k=1. . 7 TDRolodex. Cd DTPe k=1. . 9 PDCd 9 T 2 k 1 DT SR bitslice Dp. Tree. Set 1 always 1 0 0 T 1 k 0 0 . . . 1 . . . 0 … 2 2 T 1 k-1 1 1 Auth D 1 2 3 DTPe Data Cube 1 0 0 0 0 and 0 0 0 1 apple 0 0 1 0 0 April 0 0 0 0 are 0 0 0 0 2. . . 3 2/2/15. . . 1 … 0 0 3/3/14. . . 1 … 0 0 … 0 . . . 1 … 1 . D o 0 0 1. . 1 0 0 0 . . 7 0 0 0 2 3 T 1 2 … 9 . . . 0 0 0 0 1 0 0 0 0 . . . 1 2 3 4 c DTPe Document Table: 1 0 Doc T 1 P 1…T 1 P 7. . . T 9 P 1…T 9 P 7 1 … 0. . . 0 … 0. . 1. 0 0 0 . . Doc Auth… Date. . . Subj 1 …Subjm. 1 1 1/2/13. . . 0 … 0 0 0 Classical Document Table: 0 0 0 1 Pos T 1 D 1 T 1 D 2 T 1 D 3. . . T 9 D 1…T 9 D 3 0 0 Pos DTPe Position Table 0 Doc. Tbl Dp. Tree. Set Date Subj 1 Subjm 2 1 Pos D T 1 k-2 PT card D=k k=1, 2, 3 … 1 Term DTPe k=1. . 3 PTCd 7 PDcard T=k k=1. . 9 … 0 . . . Classical . . . 2 3. . . 7 TDcard P=k k=1. . 7 1 . . . 0 0 0 3 0 . . . Term 0 0 0 3 2 1 T 2, R=sell DT tfidf Dp. Tree. Set 7 0 an 0 1 0 0 … P 1 D 1 adj 0 0 0 1 1 . 75 DTPe Doc. Tbl Dp. Tree. Set indexed by (T, P)) Position 1 2 3 4 5 6 Term AAPL . . . 0 Rating of T=stock at doc date close: 1=sell, 2=hold, 3=buy 0=non-stock Term T 2, R=buy T 2, R=hold 1 0 0 Doc. Term Stock. Rating Cube T 2 k 2 1 … . . . 0 … DT SR bitmap Dp. Tree. Set T 9 3 buy 0 1 0 0 DT SR k: 3 2 1 0 -1 -2 bit: 0 0 1 1 1 0 2 1 . . . 9 tf is the +rollup of the DTPe datacube along the position dimension. One can use any measurement or data structure of measurements, e. g. , DT tfidf in which each cell has a decimal tfidf, which can be bitsliced directly into whole number bitslices plus fractional bitslices (one for each binary digit to the right of the binary point-no need to shift!) using: MOD(INT(x/(2 k), 2), e. g. , a tfidf =3. 5 is 3 . D noun adv …noun . D 2 adj Terms termfreq Data Cube noun verb s . . . 9 Term P 1 D 1 P 1 D 2 P 1 D 3. . . P 7 D 1…P 7 D 3 oc 1 DTPe Tp. Tree. Set index (D, P) Positions 1 2 … Doc 3 1 1 P 1 D 1 Doc 2 1 noun 1 0 0 Doc 1 1 0 0 0 1 0 Text Mining using p. Trees 1 DTPe Term Table: Term P 1 D 1 P 1 D 2 P 1 D 3. . . P 7 D 1…P 7 D 3 5 6 7 1 0 1 . . . 0 … 0 . . . Term buy 1 … 1 Doc 3 Doc 2 1 0 0 1 Doc 1 0 DTPe in Pp. Tree. Set index (T, D)
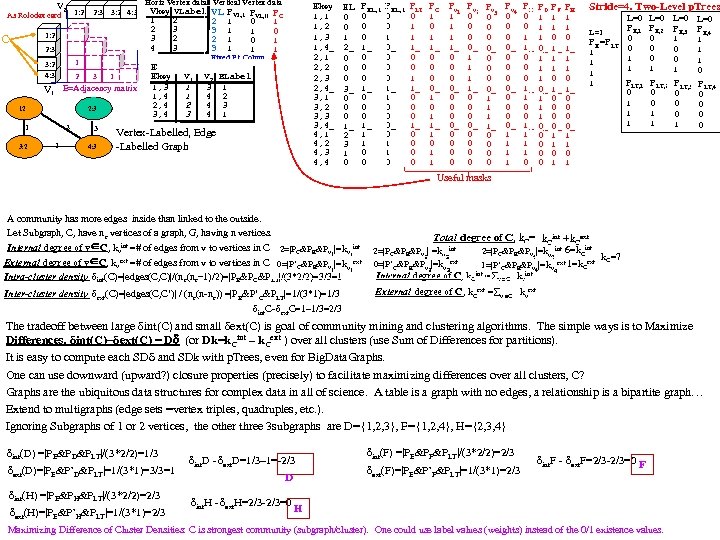 V 2 As Rolodex card Horiz Vertex data Vertical Vertex data 1: 2 2: 3 3: 2 4: 3 1: 2 C 2: 3 1 3: 2 4: 3 V 1 2 2: 3 1 2 1 1 E=Adjacency matrix 12 3: 2 3 3 4: 3 Vkey VLabel 1 2 2 3 3 2 4 3 E Ekey 1, 3 1, 4 2, 4 3, 4 V 1 1 | 2 | 3 | VL 2 3 PVL, 1 1 1 PVL, 0 0 1 Fixed Pt Colmn Ekey 1, 1 1, 2 1, 3 1, 4_ 2, 1 2, 2 2, 3 2, 4_ 3, 1 3, 2 3, 3 3, 4_ 4, 1 4, 2 4, 3 4, 4 PC 1 0 1 1 V 2 ELabel 3 1 4 2 4 3 4 1 Vertex-Labelled, Edge -Labelled Graph EL 0 0 1 2_ 0 0 0 3_ 0 0 0 1_ 2 3 1 0 PEL. , 1 0 0 0 1_ 1 1 0 0 PEL. , 1 0 0 1 0_ 0 0 0 1_ 1 0 0 0_ 0 1 1 0 PLT 0 1 1 1_ 0 0 0 1_ 0 0 PC 1 0 1 1_ 0 0_ 1 0 1 1 Pv 1 1 1_ 0 0 0 0_ 0 0 Pv 2 0 0_ 1 1_ 0 0 0 0 Pv 3 0 0 0 0_ 1 1_ 0 0 Pv 4 0 0 0 0_ 1 1 PE 0 0 1 1_ 0 0 0 1_ 1 1 1 0 PD PF PH 1 1 1 1 0 0 0_ 1_ 1_ 1 0 0 0_ 0_ 0_ 0 1 1 0 0 1 1 Stride=4. Two-Level p. Trees L=1 L=0 PE, 1 0 0 1 1 PE =PLT 1 1 1 PLT, 1 1 0 1 1 1 L=0 PE, 2 0 0 0 1 L=0 PE, 3 1 0 0 1 L=0 PE, 4 1 1 1 0 PLT, 2 0 0 1 1 PLT, 3 0 0 0 1 PLT, 4 0 0 Useful masks A community has more edges inside than linked to the outside. Let Subgraph, C, have nc vertices of a graph, G, having n vertices. Internal degree of v∈C, kvint =# of edges from v to vertices in C 2=|PC&PE&Pv |=kv int 1 1 External degree of v∈C, kvext =# of edges from v to vertices in C’ 0=|P’C&PE&Pv |=kv ext 1 1 Intra-cluster density δint(C)=|edges(C, C)|/(nc(nc− 1)/2)=|PE&PC&PLT|/(3*2/2)=3/3=1 Inter-cluster density δext(C)=|edges(C, C’)| / (nc(n-nc)) =|PE&P’C&PLT|=1/(3*1)=1/3 δint. C- δext. C=1– 1/3=2/3 Total degree of C, k. C= k. Cint +k. Cext 2=|PC&PE&Pv | =kv int 3 3 0=|P’C&PE&Pv |=kv ext 3 3 Internal degree of C, int 6=k int C 4 1=|P’C&PE&Pv |=kv ext 1=k. Cext 4 4 k. Cint = v C kvint 2=|PC&PE&Pv |=kv 4 k. C=7 External degree of C, k. Cext = v C kvext The tradeoff between large δint(C) and small δext(C) is goal of community mining and clustering algorithms. The simple ways is to Maximize Differences, δint(C)−δext(C) = D (or Dk=k. Cint – k. Cext ) over all clusters (use Sum of Differences for partitions). It is easy to compute each SD and SDk with p. Trees, even for Big. Data. Graphs. One can use downward (upward? ) closure properties (precisely) to facilitate maximizing differences over all clusters, C? Graphs are the ubiquitous data structures for complex data in all of science. A table is a graph with no edges, a relationship is a bipartite graph… Extend to multigraphs (edge sets =vertex triples, quadruples, etc. ). Ignoring Subgraphs of 1 or 2 vertices, the other three 3 subgraphs are D={1, 2, 3}, F={1, 2, 4}, H={2, 3, 4} δint(D) =|PE&PD&PLT|/(3*2/2)=1/3 δext(D)=|PE&P’D&PLT|=1/(3*1)=3/3=1 δint(H) =|PE&PH&PLT|/(3*2/2)=2/3 δext(H)=|PE&P’H&PLT|=1/(3*1)=2/3 δint. D - δext. D=1/3– 1=-2/3 D δint. H - δext. H=2/3 -2/3=0 δint(F) =|PE&PF&PLT|/(3*2/2)=2/3 δext(F)=|PE&P’F&PLT|=1/(3*1)=2/3 δint. F - δext. F=2/3 -2/3=0 F H Maximizing Difference of Cluster Densities: C is strongest community (subgraph/cluster). One could use label values (weights) instead of the 0/1 existence values.
V 2 As Rolodex card Horiz Vertex data Vertical Vertex data 1: 2 2: 3 3: 2 4: 3 1: 2 C 2: 3 1 3: 2 4: 3 V 1 2 2: 3 1 2 1 1 E=Adjacency matrix 12 3: 2 3 3 4: 3 Vkey VLabel 1 2 2 3 3 2 4 3 E Ekey 1, 3 1, 4 2, 4 3, 4 V 1 1 | 2 | 3 | VL 2 3 PVL, 1 1 1 PVL, 0 0 1 Fixed Pt Colmn Ekey 1, 1 1, 2 1, 3 1, 4_ 2, 1 2, 2 2, 3 2, 4_ 3, 1 3, 2 3, 3 3, 4_ 4, 1 4, 2 4, 3 4, 4 PC 1 0 1 1 V 2 ELabel 3 1 4 2 4 3 4 1 Vertex-Labelled, Edge -Labelled Graph EL 0 0 1 2_ 0 0 0 3_ 0 0 0 1_ 2 3 1 0 PEL. , 1 0 0 0 1_ 1 1 0 0 PEL. , 1 0 0 1 0_ 0 0 0 1_ 1 0 0 0_ 0 1 1 0 PLT 0 1 1 1_ 0 0 0 1_ 0 0 PC 1 0 1 1_ 0 0_ 1 0 1 1 Pv 1 1 1_ 0 0 0 0_ 0 0 Pv 2 0 0_ 1 1_ 0 0 0 0 Pv 3 0 0 0 0_ 1 1_ 0 0 Pv 4 0 0 0 0_ 1 1 PE 0 0 1 1_ 0 0 0 1_ 1 1 1 0 PD PF PH 1 1 1 1 0 0 0_ 1_ 1_ 1 0 0 0_ 0_ 0_ 0 1 1 0 0 1 1 Stride=4. Two-Level p. Trees L=1 L=0 PE, 1 0 0 1 1 PE =PLT 1 1 1 PLT, 1 1 0 1 1 1 L=0 PE, 2 0 0 0 1 L=0 PE, 3 1 0 0 1 L=0 PE, 4 1 1 1 0 PLT, 2 0 0 1 1 PLT, 3 0 0 0 1 PLT, 4 0 0 Useful masks A community has more edges inside than linked to the outside. Let Subgraph, C, have nc vertices of a graph, G, having n vertices. Internal degree of v∈C, kvint =# of edges from v to vertices in C 2=|PC&PE&Pv |=kv int 1 1 External degree of v∈C, kvext =# of edges from v to vertices in C’ 0=|P’C&PE&Pv |=kv ext 1 1 Intra-cluster density δint(C)=|edges(C, C)|/(nc(nc− 1)/2)=|PE&PC&PLT|/(3*2/2)=3/3=1 Inter-cluster density δext(C)=|edges(C, C’)| / (nc(n-nc)) =|PE&P’C&PLT|=1/(3*1)=1/3 δint. C- δext. C=1– 1/3=2/3 Total degree of C, k. C= k. Cint +k. Cext 2=|PC&PE&Pv | =kv int 3 3 0=|P’C&PE&Pv |=kv ext 3 3 Internal degree of C, int 6=k int C 4 1=|P’C&PE&Pv |=kv ext 1=k. Cext 4 4 k. Cint = v C kvint 2=|PC&PE&Pv |=kv 4 k. C=7 External degree of C, k. Cext = v C kvext The tradeoff between large δint(C) and small δext(C) is goal of community mining and clustering algorithms. The simple ways is to Maximize Differences, δint(C)−δext(C) = D (or Dk=k. Cint – k. Cext ) over all clusters (use Sum of Differences for partitions). It is easy to compute each SD and SDk with p. Trees, even for Big. Data. Graphs. One can use downward (upward? ) closure properties (precisely) to facilitate maximizing differences over all clusters, C? Graphs are the ubiquitous data structures for complex data in all of science. A table is a graph with no edges, a relationship is a bipartite graph… Extend to multigraphs (edge sets =vertex triples, quadruples, etc. ). Ignoring Subgraphs of 1 or 2 vertices, the other three 3 subgraphs are D={1, 2, 3}, F={1, 2, 4}, H={2, 3, 4} δint(D) =|PE&PD&PLT|/(3*2/2)=1/3 δext(D)=|PE&P’D&PLT|=1/(3*1)=3/3=1 δint(H) =|PE&PH&PLT|/(3*2/2)=2/3 δext(H)=|PE&P’H&PLT|=1/(3*1)=2/3 δint. D - δext. D=1/3– 1=-2/3 D δint. H - δext. H=2/3 -2/3=0 δint(F) =|PE&PF&PLT|/(3*2/2)=2/3 δext(F)=|PE&P’F&PLT|=1/(3*1)=2/3 δint. F - δext. F=2/3 -2/3=0 F H Maximizing Difference of Cluster Densities: C is strongest community (subgraph/cluster). One could use label values (weights) instead of the 0/1 existence values.
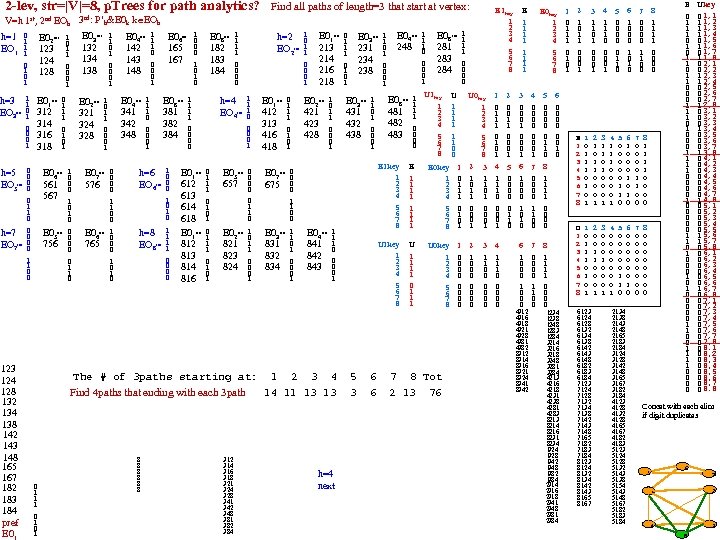 2 -lev, str=|V|=8, p. Trees for path analytics? V=h 1 st, 2 nd EOh h=1 EO 1 0 1 1 1 0 1 E 02= 123 124 128 h=3 EO 3= 1 1 0 0 0 1 E 01= 312 314 316 318 3 rd: 0 1 1 1 0 1 E 02= 321 324 328 1 1 0 0 0 1 E 04= 142 143 148 E 04= 341 342 348 1 0 1 1 0 0 0 1 1 1 1 0 0 0 0 1 E 06= 165 167 E 08= 381 382 384 h=5 EO 5= 0 0 0 1 1 0 E 06= 561 567 1 0 0 0 1 0 E 07= 576 0 0 1 1 0 0 h=6 EO 6= 1 0 0 0 1 0 h=7 EO 7= 0 0 1 1 0 0 E 05= 756 0 0 0 1 1 0 E 06= 765 1 0 0 0 1 0 h=8 EO 8= 1 1 0 0 123 124 128 132 134 138 142 143 148 165 167 182 183 184 pref E 01 1 0 0 0 1 0 E 08= 182 183 184 h=4 EO 4= 1 1 0 0 E 01= 612 613 614 618 E 01= 812 813 814 816 1 1 0 0 h=2 EO 2= 1 1 1 0 0 1 E 01= 412 313 416 418 0 1 1 1 0 1 0 1 E 05= 657 0 0 0 1 1 0 E 07= 675 E 02= 821 823 824 1 0 1 1 0 0 0 1 E 03= 831 832 834 1 1 0 0 0 1 E 01= 213 214 216 218 E 02= 421 423 428 1 0 1 1 0 0 0 1 8 8 8 E 03= 231 234 238 0 1 1 1 0 1 E 03= 431 432 438 1 1 0 0 0 1 E 04= 841 842 843 312 314 316 318 321 324 328 341 342 348 381 382 384 E 04= 248 E 08= 481 482 483 1 1 1 0 0 1 E 08= 281 283 284 1 U 1 key 1 1 1 2 1 3 4 0 0 5 0 6 0 7 8 1 1 0 0 U 1 1 1 0 0 5 3 6 6 E 0 key 1 2 3 4 5 6 7 8 1 0 1 1 1 0 1 2 0 0 1 1 0 0 0 1 3 0 0 0 1 4 0 0 0 0 1 5 0 0 0 0 0 1 1 0 6 1 0 0 0 1 0 7 0 0 1 1 0 0 8 1 1 0 0 6 1 0 0 0 7 0 0 1 1 0 0 8 1 1 0 0 E 1 1 1 1 E 0 key 1 2 3 4 5 6 7 8 1 0 1 1 1 0 1 2 1 0 1 1 0 0 0 1 3 1 1 0 0 0 1 4 1 1 1 0 0 1 U 1 1 0 1 1 1 U 0 key 1 2 3 4 5 6 7 8 1 0 0 0 0 2 1 0 0 0 0 3 1 1 0 0 0 4 1 1 1 0 0 0 7 8 Tot 2 13 76 E 1 1 1 1 U 0 key 1 2 3 4 5 6 7 8 U 1 key 1 2 3 4 5 6 7 8 1 1 1 0 0 1 h=4 next 1 1 0 0 0 1 E 1 key 1 2 3 4 5 6 7 8 0 0 1 1 0 0 0 1 1 1 0 0 0 1 The # of 3 paths starting at: 1 2 3 4 14 11 13 13 Find 4 paths that ending with each 3 path 0 1 1 1 0 1 E 1 key 1 2 3 4 5 6 7 8 P’h&E 0 k k EOh E 03= 132 134 138 1 0 1 1 0 0 0 1 Find all paths of length=3 that start at vertex: 4 312 4 316 4 318 4 321 4 328 4 381 4 382 8 314 8 316 8 321 8 324 8 341 8 342 6 0 0 0 1 0 1 234 1 238 1 248 1 283 1 284 3 216 3 218 3 248 3 281 3 284 4213 4216 4218 4231 4238 4281 4283 8 214 8 216 8 231 8 234 1 328 1 342 1 348 1 382 1 384 2 316 2 318 2 341 2 348 2 381 2 384 1 0 1 1 1 0 1 2 1 0 1 1 0 0 0 1 3 1 1 0 0 0 1 4 1 1 1 0 0 1 5 0 0 0 1 1 0 6 1 0 0 0 1 0 8 1 1 0 0 7 0 0 1 1 0 0 E 1 2 3 4 5 6 7 8 1 0 1 1 1 0 1 2 1 0 1 1 0 0 0 1 3 1 1 0 0 0 1 4 1 1 1 0 0 1 5 0 0 0 1 1 0 6 1 0 0 0 1 0 7 0 0 1 1 0 0 8 1 1 0 0 U 1 2 3 4 5 6 7 8 1 0 1 1 1 0 1 2 0 0 1 1 0 0 0 1 3 0 0 0 1 4 0 0 0 0 1 5 0 0 0 1 1 0 6 0 0 0 1 0 7 0 0 0 0 8 0 0 0 0 6123 6124 6128 6132 6134 6138 6142 6143 6148 6182 6183 6184 7123 7124 7128 7132 7134 7138 7142 7143 7148 7165 7182 7183 7184 8123 8124 8132 8134 8142 8143 8165 8167 2134 2138 2143 2148 2165 2183 2184 3128 3142 3148 3165 3167 3182 3184 4123 4128 4132 4128 4165 4167 4182 4183 5124 5128 5132 5143 5138 5154 5143 5148 5167 5182 5183 5184 E 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 1 1 0 1 0 0 0 0 0 1 1 1 1 0 0 Ukey 0 1, 1 1 1, 2 1 1, 3 1 1, 4 0 1, 5 1 1, 6 0 1, 7 1 1, 8 0 2, 1 0 2, 2 1 2, 3 1 2, 4 0 2, 5 0 2, 6 0 2, 7 1 2, 8 0 3, 1 0 3, 2 0 3, 3 1 3, 4 0 3, 5 0 3, 6 0 3, 7 1 3, 8 0 4, 1 0 4, 2 0 4, 3 0 4, 4 0 4, 5 0 4, 6 0 4, 7 1 4, 8 0 5, 1 0 5, 2 0 5, 3 0 5, 4 0 5, 5 1 5, 6 1 5, 7 0 5, 8 0 6, 1 0 6, 2 0 6, 3 0 6, 4 0 6, 5 0 6, 6 1 6, 7 0 6, 8 0 7, 1 0 7, 2 0 7, 3 0 7, 4 0 7, 5 0 7, 6 0 7, 7 0 7, 8 0 8. 1 0 8, 2 0 8, 3 0 8, 4 0 8, 5 0 8, 6 0 8, 7 0 8. 8 Concat with each elim if digit duplicates 6 5 7 2 1 4 3 8
2 -lev, str=|V|=8, p. Trees for path analytics? V=h 1 st, 2 nd EOh h=1 EO 1 0 1 1 1 0 1 E 02= 123 124 128 h=3 EO 3= 1 1 0 0 0 1 E 01= 312 314 316 318 3 rd: 0 1 1 1 0 1 E 02= 321 324 328 1 1 0 0 0 1 E 04= 142 143 148 E 04= 341 342 348 1 0 1 1 0 0 0 1 1 1 1 0 0 0 0 1 E 06= 165 167 E 08= 381 382 384 h=5 EO 5= 0 0 0 1 1 0 E 06= 561 567 1 0 0 0 1 0 E 07= 576 0 0 1 1 0 0 h=6 EO 6= 1 0 0 0 1 0 h=7 EO 7= 0 0 1 1 0 0 E 05= 756 0 0 0 1 1 0 E 06= 765 1 0 0 0 1 0 h=8 EO 8= 1 1 0 0 123 124 128 132 134 138 142 143 148 165 167 182 183 184 pref E 01 1 0 0 0 1 0 E 08= 182 183 184 h=4 EO 4= 1 1 0 0 E 01= 612 613 614 618 E 01= 812 813 814 816 1 1 0 0 h=2 EO 2= 1 1 1 0 0 1 E 01= 412 313 416 418 0 1 1 1 0 1 0 1 E 05= 657 0 0 0 1 1 0 E 07= 675 E 02= 821 823 824 1 0 1 1 0 0 0 1 E 03= 831 832 834 1 1 0 0 0 1 E 01= 213 214 216 218 E 02= 421 423 428 1 0 1 1 0 0 0 1 8 8 8 E 03= 231 234 238 0 1 1 1 0 1 E 03= 431 432 438 1 1 0 0 0 1 E 04= 841 842 843 312 314 316 318 321 324 328 341 342 348 381 382 384 E 04= 248 E 08= 481 482 483 1 1 1 0 0 1 E 08= 281 283 284 1 U 1 key 1 1 1 2 1 3 4 0 0 5 0 6 0 7 8 1 1 0 0 U 1 1 1 0 0 5 3 6 6 E 0 key 1 2 3 4 5 6 7 8 1 0 1 1 1 0 1 2 0 0 1 1 0 0 0 1 3 0 0 0 1 4 0 0 0 0 1 5 0 0 0 0 0 1 1 0 6 1 0 0 0 1 0 7 0 0 1 1 0 0 8 1 1 0 0 6 1 0 0 0 7 0 0 1 1 0 0 8 1 1 0 0 E 1 1 1 1 E 0 key 1 2 3 4 5 6 7 8 1 0 1 1 1 0 1 2 1 0 1 1 0 0 0 1 3 1 1 0 0 0 1 4 1 1 1 0 0 1 U 1 1 0 1 1 1 U 0 key 1 2 3 4 5 6 7 8 1 0 0 0 0 2 1 0 0 0 0 3 1 1 0 0 0 4 1 1 1 0 0 0 7 8 Tot 2 13 76 E 1 1 1 1 U 0 key 1 2 3 4 5 6 7 8 U 1 key 1 2 3 4 5 6 7 8 1 1 1 0 0 1 h=4 next 1 1 0 0 0 1 E 1 key 1 2 3 4 5 6 7 8 0 0 1 1 0 0 0 1 1 1 0 0 0 1 The # of 3 paths starting at: 1 2 3 4 14 11 13 13 Find 4 paths that ending with each 3 path 0 1 1 1 0 1 E 1 key 1 2 3 4 5 6 7 8 P’h&E 0 k k EOh E 03= 132 134 138 1 0 1 1 0 0 0 1 Find all paths of length=3 that start at vertex: 4 312 4 316 4 318 4 321 4 328 4 381 4 382 8 314 8 316 8 321 8 324 8 341 8 342 6 0 0 0 1 0 1 234 1 238 1 248 1 283 1 284 3 216 3 218 3 248 3 281 3 284 4213 4216 4218 4231 4238 4281 4283 8 214 8 216 8 231 8 234 1 328 1 342 1 348 1 382 1 384 2 316 2 318 2 341 2 348 2 381 2 384 1 0 1 1 1 0 1 2 1 0 1 1 0 0 0 1 3 1 1 0 0 0 1 4 1 1 1 0 0 1 5 0 0 0 1 1 0 6 1 0 0 0 1 0 8 1 1 0 0 7 0 0 1 1 0 0 E 1 2 3 4 5 6 7 8 1 0 1 1 1 0 1 2 1 0 1 1 0 0 0 1 3 1 1 0 0 0 1 4 1 1 1 0 0 1 5 0 0 0 1 1 0 6 1 0 0 0 1 0 7 0 0 1 1 0 0 8 1 1 0 0 U 1 2 3 4 5 6 7 8 1 0 1 1 1 0 1 2 0 0 1 1 0 0 0 1 3 0 0 0 1 4 0 0 0 0 1 5 0 0 0 1 1 0 6 0 0 0 1 0 7 0 0 0 0 8 0 0 0 0 6123 6124 6128 6132 6134 6138 6142 6143 6148 6182 6183 6184 7123 7124 7128 7132 7134 7138 7142 7143 7148 7165 7182 7183 7184 8123 8124 8132 8134 8142 8143 8165 8167 2134 2138 2143 2148 2165 2183 2184 3128 3142 3148 3165 3167 3182 3184 4123 4128 4132 4128 4165 4167 4182 4183 5124 5128 5132 5143 5138 5154 5143 5148 5167 5182 5183 5184 E 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 1 1 0 1 0 0 0 0 0 1 1 1 1 0 0 Ukey 0 1, 1 1 1, 2 1 1, 3 1 1, 4 0 1, 5 1 1, 6 0 1, 7 1 1, 8 0 2, 1 0 2, 2 1 2, 3 1 2, 4 0 2, 5 0 2, 6 0 2, 7 1 2, 8 0 3, 1 0 3, 2 0 3, 3 1 3, 4 0 3, 5 0 3, 6 0 3, 7 1 3, 8 0 4, 1 0 4, 2 0 4, 3 0 4, 4 0 4, 5 0 4, 6 0 4, 7 1 4, 8 0 5, 1 0 5, 2 0 5, 3 0 5, 4 0 5, 5 1 5, 6 1 5, 7 0 5, 8 0 6, 1 0 6, 2 0 6, 3 0 6, 4 0 6, 5 0 6, 6 1 6, 7 0 6, 8 0 7, 1 0 7, 2 0 7, 3 0 7, 4 0 7, 5 0 7, 6 0 7, 7 0 7, 8 0 8. 1 0 8, 2 0 8, 3 0 8, 4 0 8, 5 0 8, 6 0 8, 7 0 8. 8 Concat with each elim if digit duplicates 6 5 7 2 1 4 3 8
 6 5 1 0 1 1 1 0 1 2 0 0 1 1 0 0 0 1 2 3 1 0 0 0 1 0 1 2 3 4 1 0 0 0 1 2 4 1 0 0 1 0 1 3 2 1 0 0 0 1 2 4 1 0 0 0 0 1 2 4 3 1 0 0 0 1 3 2 4 1 0 0 0 1 3 4 1 1 0 0 0 1 3 4 2 1 0 0 0 1 4 3 1 1 0 0 0 1 4 2 1 0 0 0 0 1 4 2 3 1 0 0 0 1 4 3 2 1 0 0 0 2 1 3 2 0 0 0 1 0 0 0 2 1 3 4 0 1 0 0 0 1 6 5 0 0 0 0 2 1 4 2 0 0 1 6 7 0 0 0 0 2 1 4 3 0 1 0 0 0 2 1 6 5 0 0 0 0 2 1 4 0 1 1 0 0 2 1 3 0 1 0 0 0 2 1 6 7 0 0 0 0 2 3 1 4 0 1 0 0 0 1 3 0 1 0 0 0 2 1 6 0 0 0 0 1 0 1 2 3 4 1 0 0 0 1 4 0 1 1 0 0 1 6 0 0 1 0 1 2 3 1 0 1 0 2 3 4 2 1 0 0 0 2 4 1 3 0 1 0 0 0 2 1 0 0 1 1 0 2 4 1 6 0 0 1 0 1 2 4 3 2 1 0 0 0 3 1 2 3 0 0 0 1 0 0 0 3 1 1 0 0 0 4 1 1 1 0 0 2 3 1 0 0 0 3 1 2 4 0 0 1 0 0 2 4 1 0 0 0 0 3 1 0 1 0 2 4 3 1 1 0 0 0 2 4 1 0 1 1 0 0 1 0 2 3 4 1 1 0 0 0 2 1 0 1 1 0 0 0 3 1 2 0 0 1 1 0 0 0 5 0 0 0 1 0 3 1 4 0 1 1 0 0 3 1 4 2 0 0 1 0 0 3 1 4 3 0 1 0 0 0 3 1 6 5 0 0 0 0 3 2 1 0 0 0 3 4 1 1 0 0 0 3 1 2 4 0 0 1 0 0 7 0 0 0 1 0 4 1 0 1 1 0 0 1 0 3 2 1 0 0 1 1 0 3 1 6 0 0 1 0 1 3 1 6 7 0 0 0 0 6 1 0 0 0 1 3 1 2 6 0 0 1 0 1 3 2 4 1 0 0 1 0 3 2 4 3 1 0 0 0 1 4 3 1 1 0 0 0 3 4 1 0 1 1 0 0 1 0 3 4 1 2 0 0 1 0 0 3 4 1 6 0 0 1 0 1 5 6 1 0 0 0 1 3 4 2 1 0 0 0 0 3 4 2 1 0 0 1 0 6 1 0 1 1 1 0 0 0 4 1 2 0 0 1 1 0 0 0 4 1 2 3 0 0 0 1 0 0 0 4 1 2 4 0 0 1 0 0 4 1 3 0 1 0 0 0 4 1 3 2 0 0 0 1 0 0 0 6 7 0 0 0 0 6 5 0 0 0 0 4 1 6 0 0 1 0 1 4 1 3 4 0 1 0 0 0 4 1 6 5 0 0 0 0 3 7 6 1 0 0 0 1 0 0 4 2 1 0 0 1 1 0 4 1 6 7 0 0 0 0 2 4 4 2 1 0 0 0 0 3 2 4 1 0 0 0 0 7 4 2 3 1 0 0 0 4 2 1 3 0 0 0 1 0 0 0 4 2 1 6 0 0 1 0 1 4 3 1 0 1 0 4 2 3 1 0 0 0 1 0 4 3 2 1 0 0 0 4 2 3 4 1 0 0 0 4 3 1 2 0 0 0 1 0 0 0 5 6 1 0 1 1 1 0 0 0 4 3 1 6 0 0 1 0 1 4 3 2 1 0 0 0 1 0 5 6 7 0 0 0 0 5 6 1 2 0 0 1 1 0 0 0 5 6 1 3 0 1 0 0 0 5 6 1 4 0 1 1 0 0 6 1 3 0 1 0 0 0 6 1 2 3 0 0 0 1 0 0 0 6 1 2 4 0 0 1 0 0 6 1 4 0 1 1 0 0 6 1 3 2 0 0 0 1 0 0 0 7 6 1 0 1 1 1 0 0 0 6 1 3 4 0 1 0 0 0 6 1 4 2 0 0 1 0 0 7 6 5 0 0 0 0 6 1 4 3 0 1 0 0 0 7 6 1 2 0 0 1 1 0 0 0 7 6 1 3 0 1 0 0 0 7 6 1 4 0 1 1 0 0
6 5 1 0 1 1 1 0 1 2 0 0 1 1 0 0 0 1 2 3 1 0 0 0 1 0 1 2 3 4 1 0 0 0 1 2 4 1 0 0 1 0 1 3 2 1 0 0 0 1 2 4 1 0 0 0 0 1 2 4 3 1 0 0 0 1 3 2 4 1 0 0 0 1 3 4 1 1 0 0 0 1 3 4 2 1 0 0 0 1 4 3 1 1 0 0 0 1 4 2 1 0 0 0 0 1 4 2 3 1 0 0 0 1 4 3 2 1 0 0 0 2 1 3 2 0 0 0 1 0 0 0 2 1 3 4 0 1 0 0 0 1 6 5 0 0 0 0 2 1 4 2 0 0 1 6 7 0 0 0 0 2 1 4 3 0 1 0 0 0 2 1 6 5 0 0 0 0 2 1 4 0 1 1 0 0 2 1 3 0 1 0 0 0 2 1 6 7 0 0 0 0 2 3 1 4 0 1 0 0 0 1 3 0 1 0 0 0 2 1 6 0 0 0 0 1 0 1 2 3 4 1 0 0 0 1 4 0 1 1 0 0 1 6 0 0 1 0 1 2 3 1 0 1 0 2 3 4 2 1 0 0 0 2 4 1 3 0 1 0 0 0 2 1 0 0 1 1 0 2 4 1 6 0 0 1 0 1 2 4 3 2 1 0 0 0 3 1 2 3 0 0 0 1 0 0 0 3 1 1 0 0 0 4 1 1 1 0 0 2 3 1 0 0 0 3 1 2 4 0 0 1 0 0 2 4 1 0 0 0 0 3 1 0 1 0 2 4 3 1 1 0 0 0 2 4 1 0 1 1 0 0 1 0 2 3 4 1 1 0 0 0 2 1 0 1 1 0 0 0 3 1 2 0 0 1 1 0 0 0 5 0 0 0 1 0 3 1 4 0 1 1 0 0 3 1 4 2 0 0 1 0 0 3 1 4 3 0 1 0 0 0 3 1 6 5 0 0 0 0 3 2 1 0 0 0 3 4 1 1 0 0 0 3 1 2 4 0 0 1 0 0 7 0 0 0 1 0 4 1 0 1 1 0 0 1 0 3 2 1 0 0 1 1 0 3 1 6 0 0 1 0 1 3 1 6 7 0 0 0 0 6 1 0 0 0 1 3 1 2 6 0 0 1 0 1 3 2 4 1 0 0 1 0 3 2 4 3 1 0 0 0 1 4 3 1 1 0 0 0 3 4 1 0 1 1 0 0 1 0 3 4 1 2 0 0 1 0 0 3 4 1 6 0 0 1 0 1 5 6 1 0 0 0 1 3 4 2 1 0 0 0 0 3 4 2 1 0 0 1 0 6 1 0 1 1 1 0 0 0 4 1 2 0 0 1 1 0 0 0 4 1 2 3 0 0 0 1 0 0 0 4 1 2 4 0 0 1 0 0 4 1 3 0 1 0 0 0 4 1 3 2 0 0 0 1 0 0 0 6 7 0 0 0 0 6 5 0 0 0 0 4 1 6 0 0 1 0 1 4 1 3 4 0 1 0 0 0 4 1 6 5 0 0 0 0 3 7 6 1 0 0 0 1 0 0 4 2 1 0 0 1 1 0 4 1 6 7 0 0 0 0 2 4 4 2 1 0 0 0 0 3 2 4 1 0 0 0 0 7 4 2 3 1 0 0 0 4 2 1 3 0 0 0 1 0 0 0 4 2 1 6 0 0 1 0 1 4 3 1 0 1 0 4 2 3 1 0 0 0 1 0 4 3 2 1 0 0 0 4 2 3 4 1 0 0 0 4 3 1 2 0 0 0 1 0 0 0 5 6 1 0 1 1 1 0 0 0 4 3 1 6 0 0 1 0 1 4 3 2 1 0 0 0 1 0 5 6 7 0 0 0 0 5 6 1 2 0 0 1 1 0 0 0 5 6 1 3 0 1 0 0 0 5 6 1 4 0 1 1 0 0 6 1 3 0 1 0 0 0 6 1 2 3 0 0 0 1 0 0 0 6 1 2 4 0 0 1 0 0 6 1 4 0 1 1 0 0 6 1 3 2 0 0 0 1 0 0 0 7 6 1 0 1 1 1 0 0 0 6 1 3 4 0 1 0 0 0 6 1 4 2 0 0 1 0 0 7 6 5 0 0 0 0 6 1 4 3 0 1 0 0 0 7 6 1 2 0 0 1 1 0 0 0 7 6 1 3 0 1 0 0 0 7 6 1 4 0 1 1 0 0
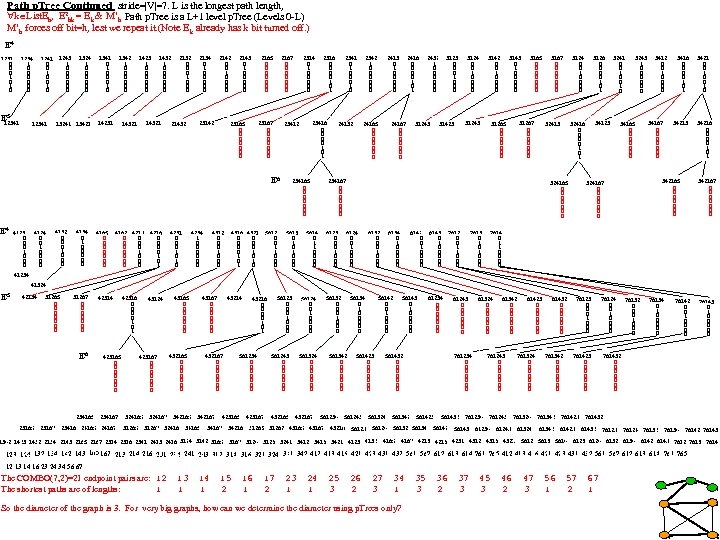 Path p. Tree Continued stride=|V|=7. L is the longest path length, k List. Eh, E 2 hk = Ek & M’h Path p. Tree is a L+1 level p. Tree (Levels 0 -L) M’h forces off bit=h, lest we repeat it. (Note E k already has k bit turned off. ) E 4 1231 0 0 0 1 0 1234 1 0 0 0 E 5 12341 1241 0 0 1 0 12341 1243 1 0 0 0 1324 1 0 0 0 1341 0 0 0 13241 1342 1 0 0 0 14231 1423 1 0 0 0 14321 2132 0 0 0 1 0 0 0 21432 2134 0 1 0 0 0 2142 0 0 1 0 0 23142 2143 0 1 0 0 0 2165 0 0 0 0 2167 0 0 0 0 23165 0 0 0 0 4123 0 0 0 1 0 0 0 4124 0 0 1 0 0 4132 0 0 0 1 0 0 0 4134 0 1 0 0 0 4165 0 0 0 0 4167 4213 0 0 0 0 1 0 0 0 4216 0 0 1 0 1 42316 0 0 1 0 1 43124 4231 0 0 0 1 0 4234 1 0 0 0 4312 0 0 0 1 0 0 0 4316 4321 0 0 0 0 1 1 0 5612 0 0 1 1 0 0 0 234165 0 0 0 0 5613 0 1 0 0 0 2316 0 0 1 0 1 2341 0 0 0 1 0 23416 0 0 1 0 1 23412 E 6 E 4 2314 0 1 0 0 0 5614 0 1 1 0 0 24132 2342 1 0 0 0 2413 0 1 0 0 0 2416 0 0 1 0 1 24167 0 0 0 0 24165 0 0 0 0 2432 1 0 0 0 31243 3123 0 0 0 1 0 0 0 3124 0 0 1 0 0 3142 0 0 1 0 0 31243 31423 3143 0 1 0 0 0 3165 0 0 0 0 31267 0 0 0 0 31265 0 0 0 0 3124 0 0 1 0 0 32413 234167 0 0 0 0 6123 0 0 0 1 0 0 0 3167 0 0 0 0 6132 0 0 0 1 0 0 0 6134 0 1 0 0 0 6142 6143 0 0 0 1 1 0 0 0 0 0 7612 0 0 1 1 0 0 0 7613 0 1 0 0 0 3241 0 0 1 0 34123 32416 0 0 1 0 1 324165 0 0 0 0 6124 0 0 1 0 0 3126 0 0 1 0 1 3243 1 0 0 0 34165 0 0 0 0 3412 0 0 1 0 0 3416 0 0 1 0 1 34167 0 0 0 0 3421 0 0 1 0 34213 34216 0 0 1 0 1 342165 0 0 0 0 324167 0 0 0 0 342167 0 0 0 0 7614 0 1 1 0 0 41234 41324 E 5 42134 31265 0 0 0 0 31267 0 0 0 0 E 6 234165 42314 423165 0 0 0 0 234167 23165 23167 23416 24165 24167 423167 0 0 0 0 432165 0 0 0 0 324165 324167 342165 31265 43167 0 0 0 0 43165 0 0 0 0 43214 432167 0 0 0 0 342167 31267 32416 34165 561234 0 0 0 0 423165 56124 0 0 1 0 0 561243 0 0 0 0 423167 34216 56123 0 0 0 1 0 0 0 43216 0 0 1 0 1 432165 561324 0 0 0 0 432167 56132 0 0 0 1 0 0 0 561342 0 0 0 0 561234 56142 0 0 1 0 0 56134 0 1 0 0 0 561423 0 0 0 0 561243 31265 31267 43165 43167 43216 56123 56143 0 1 0 0 0 61234 0 0 0 0 561432 0 0 0 0 561324 561342 61243 0 0 0 0 61324 0 0 0 0 761234 0 0 0 0 561423 561432 56124 56132 56134 56142 61342 0 0 0 0 761243 0 0 0 0 761234 761243 56143 61234 61423 0 0 0 0 761324 0 0 0 0 761342 0 0 0 0 761324 761342 61243 1342 1423 1432 2134 2143 2165 2167 2314 2316 2341 2413 2416 3124 3142 3165 3167 3124 3126 3241 3412 3416 3421 4123 4132 4165 4167 4213 4216 4231 4312 4316 4321 61324 76123 0 0 0 1 0 0 0 61432 0 0 0 0 61342 76124 0 0 1 0 0 761423 0 0 0 0 761423 76132 0 0 0 1 0 0 0 76134 0 1 0 0 0 76142 0 0 1 0 0 76143 0 1 0 0 0 761432 0 0 0 0 761432 76123 76124 76132 76134 76142 76143 5612 5613 5614 6123 6124 6132 6134 6142 6143 7612 7613 7614 123 124 132 134 142 143 165 167 213 214 216 231 234 241 243 312 314 316 321 324 341 342 413 416 421 423 431 432 561 567 612 613 614 761 765 412 413 416 421 423 431 432 561 567 612 613 614 761 765 12 13 14 16 23 24 34 56 67 The COMBO(7, 2)=21 endpoint pairs are: 12 The shortest paths are of lengths: 1 13 1 14 1 15 2 16 1 17 2 23 1 24 1 25 3 26 2 27 3 34 1 So the diameter of the graph is 3. For very big graphs, how can we determine the diameter using p. Trees only? 35 3 36 2 37 3 45 3 46 2 47 3 56 1 57 2 67 1 6 5 7 1 2 4 3
Path p. Tree Continued stride=|V|=7. L is the longest path length, k List. Eh, E 2 hk = Ek & M’h Path p. Tree is a L+1 level p. Tree (Levels 0 -L) M’h forces off bit=h, lest we repeat it. (Note E k already has k bit turned off. ) E 4 1231 0 0 0 1 0 1234 1 0 0 0 E 5 12341 1241 0 0 1 0 12341 1243 1 0 0 0 1324 1 0 0 0 1341 0 0 0 13241 1342 1 0 0 0 14231 1423 1 0 0 0 14321 2132 0 0 0 1 0 0 0 21432 2134 0 1 0 0 0 2142 0 0 1 0 0 23142 2143 0 1 0 0 0 2165 0 0 0 0 2167 0 0 0 0 23165 0 0 0 0 4123 0 0 0 1 0 0 0 4124 0 0 1 0 0 4132 0 0 0 1 0 0 0 4134 0 1 0 0 0 4165 0 0 0 0 4167 4213 0 0 0 0 1 0 0 0 4216 0 0 1 0 1 42316 0 0 1 0 1 43124 4231 0 0 0 1 0 4234 1 0 0 0 4312 0 0 0 1 0 0 0 4316 4321 0 0 0 0 1 1 0 5612 0 0 1 1 0 0 0 234165 0 0 0 0 5613 0 1 0 0 0 2316 0 0 1 0 1 2341 0 0 0 1 0 23416 0 0 1 0 1 23412 E 6 E 4 2314 0 1 0 0 0 5614 0 1 1 0 0 24132 2342 1 0 0 0 2413 0 1 0 0 0 2416 0 0 1 0 1 24167 0 0 0 0 24165 0 0 0 0 2432 1 0 0 0 31243 3123 0 0 0 1 0 0 0 3124 0 0 1 0 0 3142 0 0 1 0 0 31243 31423 3143 0 1 0 0 0 3165 0 0 0 0 31267 0 0 0 0 31265 0 0 0 0 3124 0 0 1 0 0 32413 234167 0 0 0 0 6123 0 0 0 1 0 0 0 3167 0 0 0 0 6132 0 0 0 1 0 0 0 6134 0 1 0 0 0 6142 6143 0 0 0 1 1 0 0 0 0 0 7612 0 0 1 1 0 0 0 7613 0 1 0 0 0 3241 0 0 1 0 34123 32416 0 0 1 0 1 324165 0 0 0 0 6124 0 0 1 0 0 3126 0 0 1 0 1 3243 1 0 0 0 34165 0 0 0 0 3412 0 0 1 0 0 3416 0 0 1 0 1 34167 0 0 0 0 3421 0 0 1 0 34213 34216 0 0 1 0 1 342165 0 0 0 0 324167 0 0 0 0 342167 0 0 0 0 7614 0 1 1 0 0 41234 41324 E 5 42134 31265 0 0 0 0 31267 0 0 0 0 E 6 234165 42314 423165 0 0 0 0 234167 23165 23167 23416 24165 24167 423167 0 0 0 0 432165 0 0 0 0 324165 324167 342165 31265 43167 0 0 0 0 43165 0 0 0 0 43214 432167 0 0 0 0 342167 31267 32416 34165 561234 0 0 0 0 423165 56124 0 0 1 0 0 561243 0 0 0 0 423167 34216 56123 0 0 0 1 0 0 0 43216 0 0 1 0 1 432165 561324 0 0 0 0 432167 56132 0 0 0 1 0 0 0 561342 0 0 0 0 561234 56142 0 0 1 0 0 56134 0 1 0 0 0 561423 0 0 0 0 561243 31265 31267 43165 43167 43216 56123 56143 0 1 0 0 0 61234 0 0 0 0 561432 0 0 0 0 561324 561342 61243 0 0 0 0 61324 0 0 0 0 761234 0 0 0 0 561423 561432 56124 56132 56134 56142 61342 0 0 0 0 761243 0 0 0 0 761234 761243 56143 61234 61423 0 0 0 0 761324 0 0 0 0 761342 0 0 0 0 761324 761342 61243 1342 1423 1432 2134 2143 2165 2167 2314 2316 2341 2413 2416 3124 3142 3165 3167 3124 3126 3241 3412 3416 3421 4123 4132 4165 4167 4213 4216 4231 4312 4316 4321 61324 76123 0 0 0 1 0 0 0 61432 0 0 0 0 61342 76124 0 0 1 0 0 761423 0 0 0 0 761423 76132 0 0 0 1 0 0 0 76134 0 1 0 0 0 76142 0 0 1 0 0 76143 0 1 0 0 0 761432 0 0 0 0 761432 76123 76124 76132 76134 76142 76143 5612 5613 5614 6123 6124 6132 6134 6142 6143 7612 7613 7614 123 124 132 134 142 143 165 167 213 214 216 231 234 241 243 312 314 316 321 324 341 342 413 416 421 423 431 432 561 567 612 613 614 761 765 412 413 416 421 423 431 432 561 567 612 613 614 761 765 12 13 14 16 23 24 34 56 67 The COMBO(7, 2)=21 endpoint pairs are: 12 The shortest paths are of lengths: 1 13 1 14 1 15 2 16 1 17 2 23 1 24 1 25 3 26 2 27 3 34 1 So the diameter of the graph is 3. For very big graphs, how can we determine the diameter using p. Trees only? 35 3 36 2 37 3 45 3 46 2 47 3 56 1 57 2 67 1 6 5 7 1 2 4 3


